基于飞腾M6678的向量数学库优化技术研究∗
2021-04-06
(中船重工(武汉)凌久电子有限责任公司 武汉 430074)
1 引言
飞腾M6678为国产化数字信号处理器(Digital Signal Processor,DSP),单核心的浮点理论运算速度达到16GFLOPS,具有功能强大的FFT协处理器,同时兼容TMS320C6678处理器的SIMD指令集。
基础数学库是高性能计算的核心基础软件。与传统的标量运算不同,向量数学库为提升大点数下的数学运算性能而构建,向量化带来的加速比高,性能提升明显。这对于促进国产化芯片行业的蓬勃发展至关重要。向量数学库已经在ARM微处理器[1~2]和国产CPU[3]平台进行了向量化优化[4~6]的尝试。
虽然处理器架构不同,但是向量化的许多方法都是类似的,比如地址对齐[7]、使用SIMD指令[8]和软件流水[9~10]。其中地址对齐提高了访存的速度,SIMD指令利用了指令的位宽[11]实现了数据运算的并行,而软件流水,类似于工厂的流水线,函数循环并非顺序执行,第一次循环还未执行完毕,第二次循环已经开始了。但是,仅有这些方法,无法在DSP上完成向量化优化。本文针对飞腾M6678处理器,构建向量数学库。
目前,飞腾M6678处理器上能够运算的数学函数库有两个,一个是标准C数学函数库,一个是TI公司提供的MATHLIB函数库。上述两个数学函数库都只能满足标量运算的性能要求,当进行大点数的向量数学运算时,无法充分利用DSP的并行运算能力。前者在向量化运算过程中效率低下,后者将代码由内联函数封装,编译器可以根据算法的实现,自行尝试向量化的优化。
数学运算在飞腾M6678处理器上进行性能测试。测试点数选择1024,结果如表1。
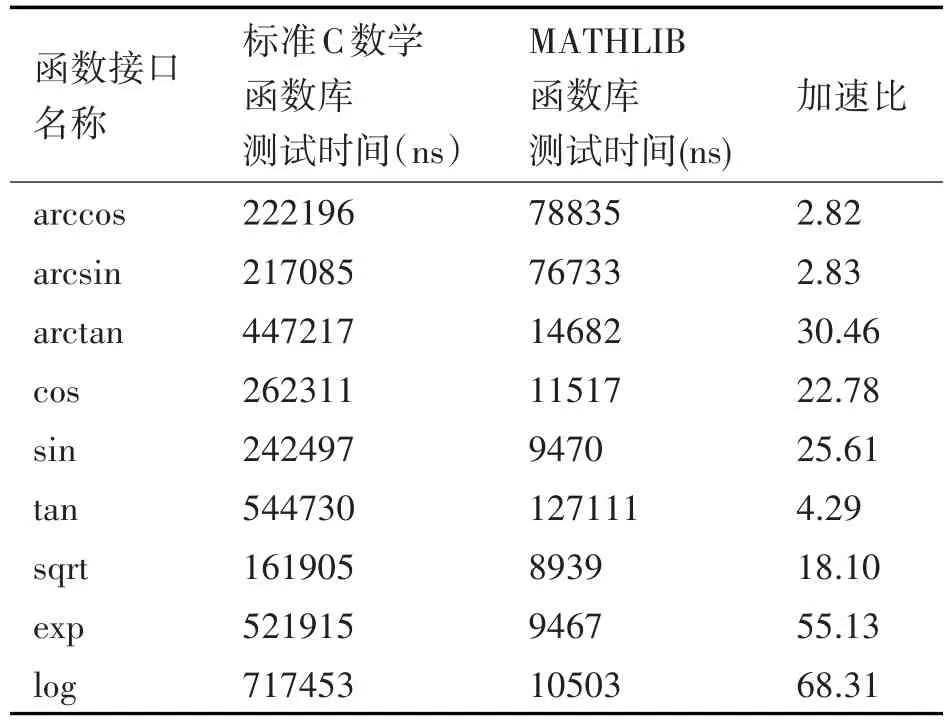
表1 数学运算性能测试
由表1可知,ARCTAN、COS、SIN、EXP和LOG运算的加速比均超过了20,向量化程度高,可向量化的空间小[12]。因此,本文性能优化的重点应该是ARCCOS、ARCSIN、TAN和SQRT。
本文以MATHLIB函数库为基础,结合DSP的硬件特性,对数学函数进行向量化优化,实现了高性能向量数学库。
2 函数实现
数学库常用的实现方法有级数法、迭代法、查表法、有理数逼近法、逐位法、CORDIC[13]算法。但是以上算法都各自存在自己的问题,级数法和迭代法运算量大,查表法占用空间大,只能计算一定区间内的三角函数,有理数逼近法的向量化空间小,逐位法和CORDIC算法适合只有加法器,没有乘法器的处理器架构。文献[14]算法实现了双精度浮点数学运算的向量化,然而大多数数学运算只需要单精度就足够了。本文实现的是单精度浮点向量数学库,ARCCOS、ARCSIN选用泰勒级数法实现,SQRT选用牛顿迭代法[15]实现,TAN采用公式SIN/COS实现。DSP良好的乘加运算能力,很好地满足了级数法和迭代法对运算能力的要求。
上述4个函数的实现均需要进行求倒数或者求平方根倒数的运算。为提高函数运算性能,不同于简单使用符号“/”,本文用DSP指令[16]RCPSP和RSQRSP实现,其中RCPSP进行浮点的求倒数运算,RSQRSP进行浮点的求平方根倒数运算。一方面,编译器省去了解码、译码的时间,另一方面,能够正常开启软件流水。
上述指令经过测试后发现,运算性能相较于符号“/”提高了两个数量级,但是运算精度很低,达不到大多数应用场景的要求。为了提高运算性能的同时保证数据精度,引入牛顿迭代法。
不加推导的给出牛顿迭代法的基本公式为

已经证明,如果是连续的、并且待求的零点是孤立的,那么该零点周围存在一个区域,只要初始值位与这个邻近区域,那么牛顿法必定收敛。
牛顿迭代法具有平方收敛的性能,这意味着,牛顿法每迭代一次,计算结果精度将提高一倍。FLOAT类型有效位数为7位,RCPSP和RSQRSP运算精度为1/256,即有效位数为2位,使用牛顿法迭代2次,即可以完全满足精度要求。
3 函数优化
3.1 确定算法的性能瓶颈
优化的第一步是找到算法的性能瓶颈。以开平方运算为例,对迭代法的代码进行性能分析。MATHLIB源码如下:


表2统计了单次循环体内,各个计算单元所需要的时钟周期数。

表2 原单次循环性能分析
由于各个运算单元可以并行执行,那么循环体执行一次的周期数就等于表中最大的时钟周期数。由表2可知,循环体执行一次的周期数等于7。多达7次的跨组寄存器访问导致性能下降。同时,乘法计算单元使用负荷也很大。另外,RSQRSP执行时间远低于牛顿迭代法执行时间。
因此,过多的跨组寄存器访问,是开平方运算的性能瓶颈。
3.2 均衡负载
均衡负载的方法根据M6678的计算单元结构所提出。
如图1 DSP内核中有两套4个截然不同的处理单元,当处理float型数据时,M处理乘法运算、L处理加法和转换运算、S处理比较和倒数运算、D处理数据的加载和存储。这8个处理单元可以独立并行执行。但是,计算单元访问不同组的寄存器,会导致运算时间的消耗。

图1 M6678内核数据处理示意图
均衡负载,要求A、B两组处理单元的使用次数大体一致,不要出现某个处理单元的负荷过大,其他处理单元在旁边等待的情况。
本文采用循环展开的方式使得负载均衡。循环展开,就是减少循环次数的同时,将循环体扩大。以开平方运算为例,将循环体扩大一倍,使得原来的第一次循环由A组执行,原来的第二次循环由B组执行。这样一来,循环体内不再需要跨组寄存器的访问。同时,循环展开前的乘法单元在一次循环内,共执行了9次,其中A组执行了5次,B组执行了4次,等待了1次,此时负载不均衡。循环展开后,A组和B组的乘法单元均执行了9次,没有等待时间。也就是说,原本两次循环,共计10次乘法计算的时间,循环展开后,只需要9次乘法计算的时间了。
3.3 指令级SIMD优化
解决了负载均衡的问题,本文使用指令级SIMD优化方法着手解决第二个瓶颈,即9次乘法运算。
通常需要运算的FLOAT、INT型数据都是32位,甚至有16位的SHORT类型,然而M6678的每个运算单元均是64位位宽。因此,调用SIMD指令集,可以充分利用运算单元的位宽,一个指令在一个时钟周期内,可以同时完成几个数据的运算。同时,使用指令集也节省了编译器调用指令的时间。编译器可以在一个时钟周期内完成指令预取、取指、译码、访问、读取、执行的所有操作。
前文提到的开平方运算中,通过AMEMD8_CONST、FTOD、DMPYSP、DSUBSP指令完成迭代法的数据位并行,减少乘法计算单元的使用负荷。
3.4 减小循环体的条件分支
开平方运算经过前两个小节的优化,计算单元的占用达到了最小,但是由于两个分支条件的存在,软件流水不能完全开启。
为了减小循环体的条件分支,本文将原来的循环体分成了两个小的循环体,第一个循环体进行计算,第二个循环体进行特殊值的处理。
至此,开平方运算完成了向量化的优化。优化后的代码性能分析如下。
由表3可知,循环体内执行的最大时钟周期数等于乘法计算单元执行的周期数9,此时A、B两组乘法计算单元负载均衡。数据位并行和循环展开都分别将循环点数减少了2倍,因此表2中循环体执行1次,相当于表1中循环体执行4次。这意味着,原有代码执行4次循环共计28个时钟周期的操作,优化后9个时钟周期就完成了。当然,实际优化的效率并没有这么高,还应考虑条件分支处理循环产生的耗时。
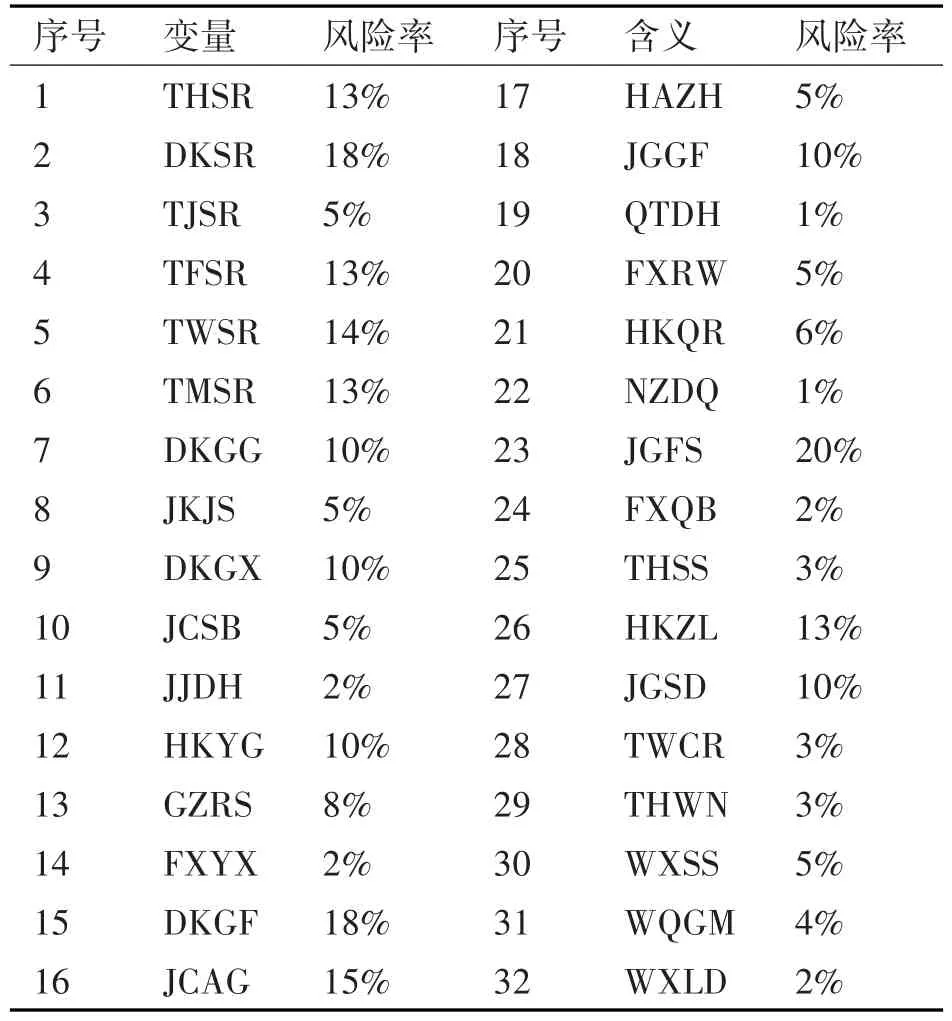
表2 通用航空安全风险计算结果
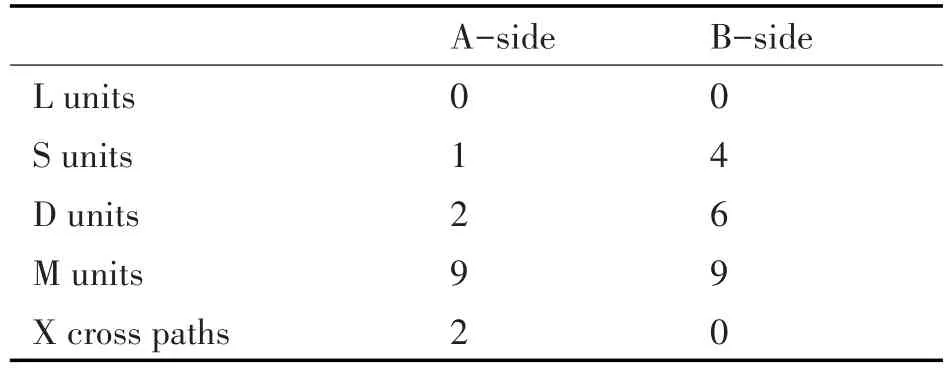
表3 优化后单次循环性能分析
4 性能测试与评价
本文测试的硬件平台为飞腾M6678开发板,主频1.0GHz,开发调试环境为CCS 5.5,数据运行地址为MSMC(多核共享内存)。
设计测试MATHLIB函数库和本文优化的向量数学库在M6678单核条件下的运算能力。测试数据规模分别为256、512、1024、2048,记录两个数学库函数接口的执行时间,求出不同数据规模下,向量数学库相较于MATHLIB函数库的加速比。最后,求出不同数据规模下加速比的平均值,记录于表4。
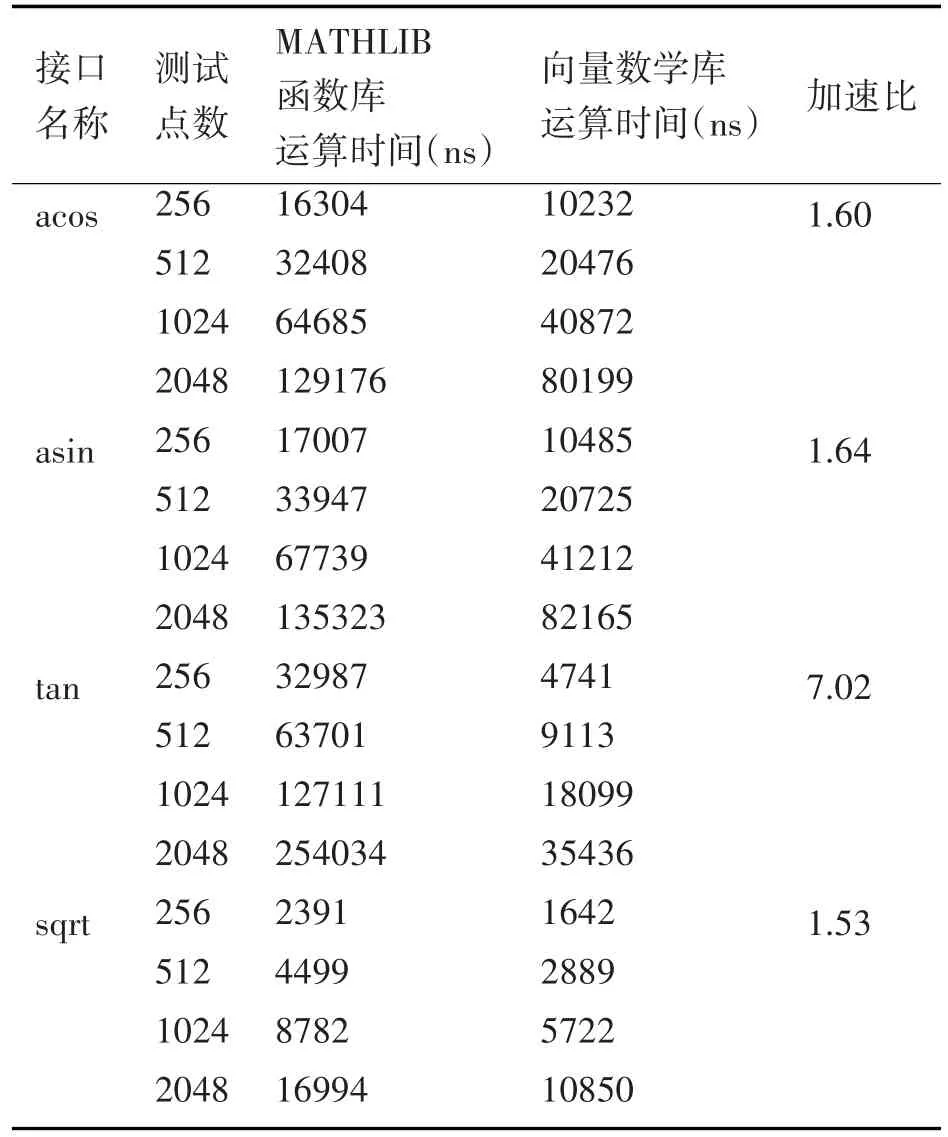
表4 部分典型向量数学运算的性能测试
由于MATHLIB函数库各个接口已有的向量化程度不同,所以加速比也不相同。但是总地来说,优化效果是显著的。
正确性方面,在浮点数据有效位数之内,向量数学库与MATHLIB函数库结果完全相等。这表明,向量数学库完全能够胜任大多数应用对运算精度的要求。
5 结语
本文针对飞腾M6678平台下的向量数学库,采用了DSP指令和牛顿迭代法进行改进。通过深入分析算法的性能瓶颈,提出了通用的SIMD优化方法,以及结合硬件特性的优化方法,充分利用了硬件资源,显著提升了向量数学库的运算性能。此外,总结的优化方法包括性能瓶颈的分析、循环展开、SIMD指令的使用和减小循环体分支,在飞腾M6678平台下具有通用性,适用于大多数情况下的算法优化。下一步工作将主要围绕更为复杂的信号处理和图像处理向量库进行性能优化。
