密排六方钛合金宏观织构的超声分析方法
2021-04-06张国宁何方成
张国宁 卢 超 何方成 梁 菁 王 晓*
(1.南昌航空大学 测试与光电工程学院,南昌 330063;2.北京航空材料研究院,北京 100095)
0 引言
钛合金比强度高,且具有良好的耐腐蚀性和耐热性,成为工程中经常使用的材料之一。但是钛合金在各种热机械加工过程中(例如轧制,拉伸和淬火等)都会存在织构的产生[3-5]。所以,钛合金通常表现出具有正交宏观对称性的各向异性微观结构[6-8],使其制件在使用过程中提前失效的可能性大大增加,从而造成严重危害。
多年来,国内外评价材料织构使用电子背散射衍射(Electron Backscattering Diffraction,简称EBSD)方法居多[9],但此方法无法实现无损伤的在线检测,且检测成本昂贵。超声波技术正在开发替代品,但目前国内外鲜有人研究,且研究主要以立方晶系多晶材料为主。国内南昌大学黄模佳等人[10-11]对立方晶粒的多晶集合体中弹性张量与超声波波速的关系进行研究,推导出了织构系数与超声波波速的关系。英国帝国理工大学的Bo Lan等人[12]利用超声波速度获得立方多晶材料织构的广义球谐卷积方法,解决了一般情况下利用单晶特性和多晶取向分布函数预测多晶体波速的正向问题,同时其取向分布系数可以根据具有晶体对称性的多晶体的波速反向确定。
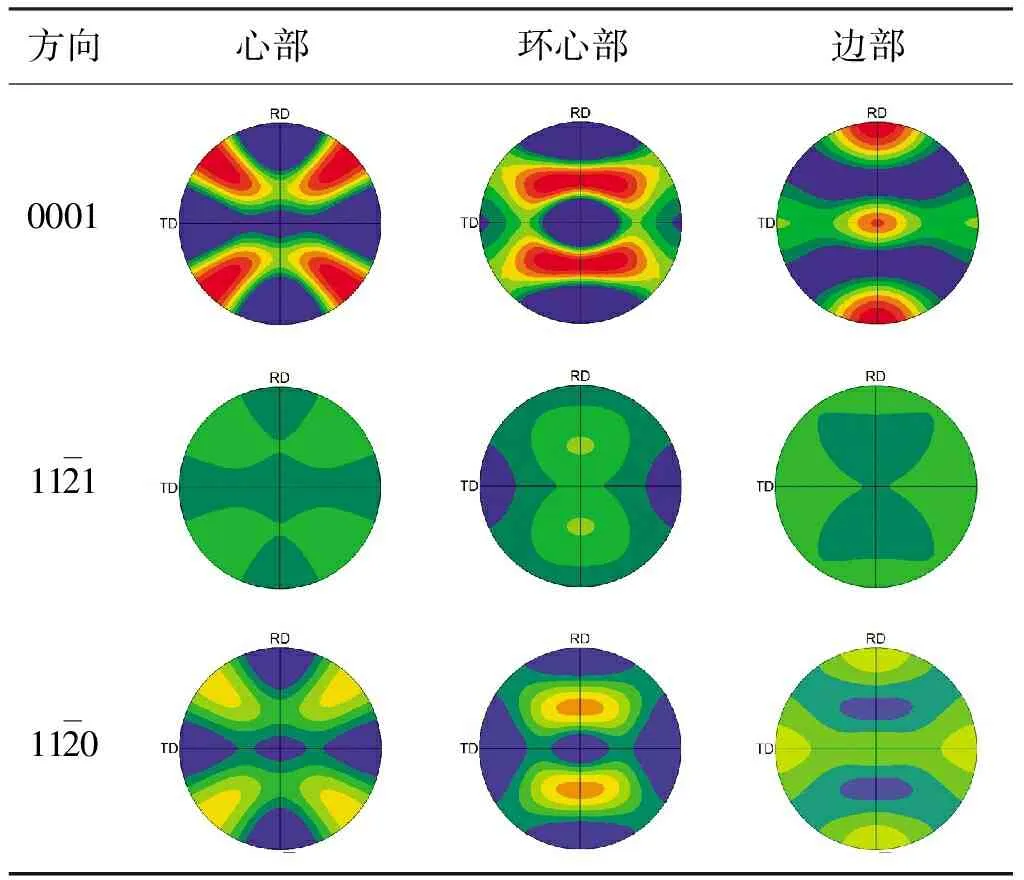
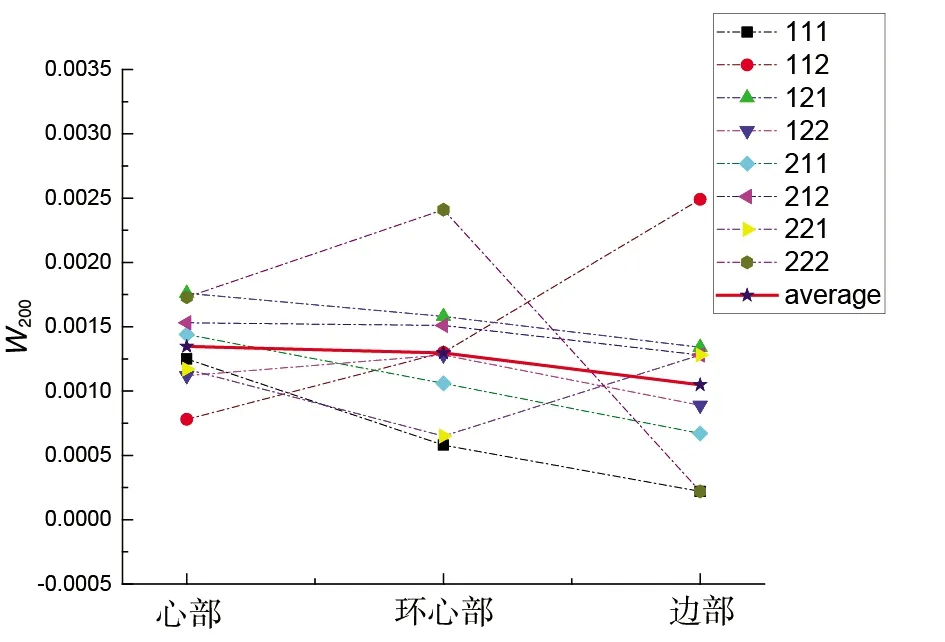
利用微晶取向分布函数(crystal orientation distribution function,简称CODF)对织构定量描述,该函数可以在一系列广义球谐函数中展开[12]。扩展的系数Wlmn可以充分表征材料的织构,其中-∞ TA19是美国Ti6242合金的中国化名称,其组织结构主要为α相,具有密排六方晶体结构(hcp),属近α型钛合金。 分别对8件饼状TA19钛合金锻件进行了两种试验分析,一种是底波幅值成像C扫描,另一种是声速成像C扫描,经过对比发现在表征材料织构差异方面,声速成像C扫图可呈现更加丰富的信息。采用小角度临界值纵波与表面瑞利波对试样典型的位置进行织构系数的测量。从另一角度证明声速表征织构差异的可行性。 试验采用规格为φ300 mm×20 mm的8件圆饼状TA19钛合金锻件。使用PAC公司生产的水浸超声扫描设备对其进行试验。试验使用的超声探头规格为:中心频率5 MHz;晶片直径为9.525 mm。沿x3轴方向分别采用时间差模式和幅值模式进行扫查,时间差模式采用试样上下表面一次回波的声程差进行成像,幅值模式采用一次底回波幅值进行成像,C扫描中超声探头的移动步进设置为0.3 mm,即成像分辨率为0.3 mm。试样如图1所示。 (a)三维圆饼状试样结构图 (b)试样实物图 (1) 这里 (2) 这里 (4) η6-8η4+8(3-2ζ2)η2-16(1-ζ2)=0 (6) 其中: (7) 可以修改式(3)~(5)以获得在其余主平面x1=0和x2=0上传播的波的相速度。在x3=0平面中,定义了γ=0为x1轴方向。 (A1) 这里: (A2) (A3) A2=C11-7C12+C33+5C13-4C44, A3=-5C11+7C12+2C33-4C13+6C44, B=C11+C33-2C13-4C44, 其中,C11、C33、C44、C12和C13是单晶弹性常数。B系数是单晶弹性常数的组合。瑞利波系数A2222,A2233,A23和A3333由Delsanto和Clark提出[15]。可写为, (B1) A3333=A2222(1-u/p), 这里: (B2) α0=[2(u-1)(u-p)]/[u(2u2-3up+u+2p-2)] β0=p/(2-2p)+1/u (C1) 这里: 这里: c0=c33(c11+c12)-2c132. Cij和Sij分别是六方晶系结构的单晶弹性常数和柔顺常数,A1,A2,A3,A23,A2222,A2233,A3333这些系数是单晶弹性常数的组合。 V(γ)=V0+P+Qcos(2γ)+Rcos(4γ) (8) ∏=V0+P (9) 表1 两种超声波模式下的Zi系数 根据等式(10)和等式(A2),获得以下方程组: 等式(11)可以计算出α六方晶系多晶材料的五个织构系数W200,W220,W400,W420,W440,作为∏=V0+P、Q、R的函数。通过测量在材料主平面上传播的两种超声模式的相速度的角变化,基于公式(8)拟合出∏、Q、R的值。 最常见的情况是,只有一个主对称平面可用于测量,例如在薄板上。板的表面通常与一个主对称平面重合,并且通常定义为x3=0平面。然后,可以使用两个不同的超声模式确定五个纹理系数Wlmn,在这种情况下P,Q和R值可用于估计五个纹理系数。 使a,b∈(L,R),且a≠b,即a和b对应于x3=0平面上传播的两种不同模式。使用等式(11)得到: (12) 表2中列举了4块钛合金锻件的时间差模式和幅值模式C扫描成像结果,扫查结果根据特征值的大小通过彩虹色标进行表示,红色区域代表特征值高,蓝色区域代表特征值低。其中,表2中第一行分别为4块钛合金试块的超声底波幅值C扫描成像结果,可以明显看出,钛合金锻件一次底反射波衰减是均匀的。表2中第二行图像为钛合金锻件的超声波声速C扫描结果成像,整个速度变化范围为6 100 m·s-1~6 250 m·s-1,钛合金锻件试样中心部分(心部),环中心部分(环心部),以及边缘处(边部),呈现出明显的颜色差异,通过色标可知,饼状TA19钛合金锻件沿x3=0轴方向的声速值,呈现出以圆心为中心的环状分布特征,不同环状半径的区域有这不同的声速值。三处位置如图2所示,图中1为心部、2为环心部、3为边部。 表2 4块钛合金锻件的两种特征值C扫描成像结果 图2 钛合金锻件试样不同测试位 样品试块为8件饼状TA19钛合金锻件,每块试样规格为φ300 mm×20 mm,其组织结构主要为α相,具有密排六方晶体结构。 采用泛美公司生产的model5800宽频信号发生器与Lecroy数字示波器分别对8块试样进行声速测量,选用的探头分别为中心频率5 MHz的小角度纵波探头与中心频率5 MHz的瑞利波探头。均采用一发一收接触探头进行测量,并将两个探头粘接到一起,如图3所示,此方法最大限度缩小声速传播范围,使织构系数在统计上更具有意义。根据表Ⅱ声速扫描结果,在x3=0主平面上心部、环心部、边缘部分别选一个位置,自x1=0轴为起始角,以10°为增量,顺时针在19个不同的传播方向上测量相速度。探头旋转时,中心轴线始终位于检测区域中心处,操作方式如图3所示。在测量期间,温度恒定在±0.1 ℃之内。 (a)试验物品摆放图示 测得试样表面三个局部区域的纵波与表面波随角度变化的相速度值和最小拟合曲线,从中提取出拟合系数∏、Q、R值,如图4所示。三个系数分别有以下特征:与角度无关的有效系数∏和对应于第二和第四角谐波的两个系数Q和R。对于平面上传播的每种类型的超声波,这些系数都有所不同。由于我们测量了两种在三个区域心部、环心部、边缘部上传播的超声波,所以每块试样上,∏、Q和R分别具有六个不同的值,如表3所示。使用这些系数计算织构系数,如表4所示。 图4 112试样上,两种波形分别在三个不同位置19个传播方向下测量的相速度,实线是基于公式(8)的最小二乘拟合曲线 表3 112试样上,三个区域两种超声波的拟合系数∏、Q、R值 表4 112试样三个位置测得的织构系数 2.3.1 构建极图 测量极密度分布并绘成极图是分析观测织构的基本方法。极密度分布函数ρHKL(α,β)为: (0≤α≤π,0≤β≤2π) (13) (14) (15) K(α,β)是球谐函数,表达式为: (17) 我们现知五位Wlmn系数,W200,W220,W400,W420,W440。可归纳为,n全部为0,l分别取两种值,2和4,当l取值为2时,m取0和2,当l取值4时,m取值为0,2,4。 通过公式(14)~(17)可将连带勒让德函数和球谐函数共轭复数展开,将结果带入公式(13)可得到极密度分布函数的展开结果,从而画出极图。 以112试块为例,分别画出三处测量点的极图,如表5所示。 表5 112试样三个位置的计算极图 2.3.2 各织构系数在不同位置的取值分析 均匀各向同性材料的织构系数为0,故织构系数的绝对值可表征某区域织构的大小。本文单独分析各位织构系数绝对值在试样三种位置的差异。为使结果更具有一般性,我们选用8块试块,将各个试块相同位置的织构系数绝对值做平均,分析单个织构系数在不同位置处的特征差异,如图5所示。 (a)W200织构系数 根据图5中数据汇总的结果可以发现,在饼状TA19锻件试样的不同位置处,W220、W420、W440三位织构系数的取值均有明显差异。其中: 1)对于W220系数,从平均值上看,心部位置的W220系数绝对值明显小于环心和边部位置的W220系数绝对值。心部位置的W220系数绝对值普遍小于0.001,环心部位置的W220系数绝对值普遍大于0.001 5,而边部位置的W220系数绝对值在0.000 5~0.003 5之间无规则(随机)分布。 2)对于W420系数,从平均值上看,心部位置的W420系数绝对值明显小于环心和边部位置的W420系数绝对值。心部位置的W420系数绝对值普遍小于0.005。而环心部和边部位置的W420系数绝对值在0~0.014之间无规则自由(随机)分布。 3)对于W440系数,从平均值上看,心部位置的W440系数绝对值明显大于环心与边部位置的W440系数绝对值,且心部位置的W440系数绝对值普遍大于0.015,而环心与边部的W440系数绝对值普遍小于0.015; 4)对于W200系数,从平均值上看,三个位置的W200系数绝对值差异较小。从分布区间上看,W200系数绝对值在心部位置处的分布区间较小,无规则自由分布在0.000 7~0.001 7之间,而在环心与边部位置分布区间较大,均无规则自由分布在0.000 2~0.002 5之间。 5)对于W400系数,从平均值上看,三个位置的W400系数绝对值差异较小。从分布区间上看,W400系数绝对值在心部位置处的分布区间较小,无规则自由分布在0.003~0.009之间,而在环心与边部位置分布区间较大,均无规则自由分布在0.001~0.013之间。 织构系数绝对值的差异,说明了饼状TA19锻件试样不同位置的织构有这明显的差异,与上文中声速C扫描结果对应。 (1)单一方向的声速C扫图可以反映出TA19钛合金锻件各位置的织构差异。 (2)小角度临界值纵波和瑞利波,可以表征材料近表面的宏观晶粒取向分布,并能精确测量出W200,W220,W400,W420,W440五位织构系数。 (3)通过所测得的四阶织构系数,可通过连带勒让德函数和球谐函数计算出相应的织构极图。 (4)在不同的声速C扫描结果处,各位织构系数绝对值的分布区间有所差异,且W220、W420、W440三位织构系数绝对值均可以很明显的呈现出不同位置处的织构差异。1 试验方法
1.1 幅值与声速成像C扫描

1.2 随角度变化的相速度与等效弹性常数的关系
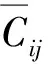
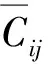
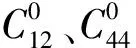
1.3 等效弹性常数与织构系数的关系
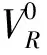

1.4 织构系数Wlmn的测量
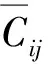
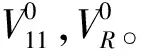
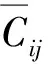



2 试验结果与分析
2.1 幅值和声速成像C扫描结果


2.2 取向织构系数的计算





2.3 结果分析


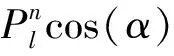
3 结论
