An unsupervised pattern recognition methodology based on factor analysis and a genetic-DBSCAN algorithm to infer operational conditions from strain measurements in structural applications
2021-04-06JuanCarlosPERAFALOPEZJuliaSIERRAPEREZ
Juan Carlos PERAFA´ N-LO´ PEZ, Julia´n SIERRA-PE´ REZ
Grupo de Investigacio´n en Ingenierı´a Aeroespacial,Universidad Pontificia Bolivariana,Circular 1 70-01,Medellı´n 050031,Colombia
KEYWORDS Clustering;DBSCAN;Factor analysis;FBGs;Pattern recognition;Strain field
Abstract Structural Health Monitoring (SHM) suggests the use of machine learning algorithms with the aim of understanding specific behaviors in a structural system.This work introduces a pattern recognition methodology for operational condition clustering in a structure sample using the well known Density Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm.The methodology was validated using a data set from an experiment with 32 Fiber Bragg Gratings bonded to an aluminum beam placed in cantilever and submitted to cyclic bending loads under 13 different operational conditions(pitch angles).Further,the computational cost and precision of the machine learning pipeline called FA+GA-DBSCAN (which employs a combination of machine learning techniques including factor analysis for dimensionality reduction and a genetic algorithm for the automatic selection of initial parameters of DBSCAN) was measured. The obtained results have shown a good performance, detecting 12 of 13 operational conditions, with an overall precision over 90%.
1. Introduction
Aircraft systems are designed to last under operation for long periods of time. However, during these cycles, unexpected loads are presented in structures, for which, an anomaly or a damage occurrence appear without a proper corrective action,deriving often in serious incidents or accidents.
Therefore,a constant monitoring of aerospace structures is decisive for aircraft’airworthiness.Such need of having global information about the structure’s health can impact the way maintenance is performed today. Non Destructive Testing(NDT) methods, have been the cutting edge of damage detection in the last few decades but some of those methods are time consuming and imply high costs. Structural Health Monitoring (SHM) can be assumed as the natural evolution of NDT methods. SHM process can help in the optimization of structures, weight reduction, and improvement the economic income by reducing the maintenance expenditures.1
SHM consists of implementation of a strategy for damage prognosis avoiding the human error factor by the automation of processes. Nowadays, SHM is one of the most promising mechanisms of maintenance to prevent and forestall flaws dissemination in many kind of structures.2.
When a structure is affected by an external or internal load,the body can be mechanically deformed, this phenomenon is related to an implicit state of strain also known as ‘‘strain field”and it changes as function of the imposed loads.Inherent factors to the regular operation of a system such as a change in the direction of the load may also lead to a change in the strain field. These strain fields can be inferred by means of discrete strain measurements gathered by strain sensors such as Fiber Bragg Gratings (FBGs).
In addition, damage occurrence in a structural system can change the local or global stiffness, hence, the strain field may also vary. Here lies the necessity to infer the strain field under regular operational conditions for a pristine condition before detecting damage (outline detection). The continuous measuring of strains in a structure using Fiber Optic Sensors(FOS) is a promising technology for SHM due to their small size and high sensitivity to strain.3Strain-based SHM is one of the methodologies in which clustering techniques may be involved as novelty detection or anomaly detection.4–7
Currently, pattern recognition has become an important tool in many fields of science and aerospace is not the exception. Pattern recognition algorithms in the framework of SHM are commonly categorized in two major groups: supervised pattern recognition and unsupervised pattern recognition. The last one includes methodologies such as clustering which is commonly used when labeled data are not available,and it may lead to novelty detection algorithms. With the use of a novelty detection algorithms it is possible to infer information about the presence or absence of damage in a structure.8
Several approaches have been developed and implemented in structures to characterize operational conditions and further to infer the damage occurrence through an structural monitoring system;those approaches are included in one of the following general subjects9: SHM, condition monitoring and machinery diagnostics,10non destructive evaluation,11statistical process control and damage prognosis.12
The implementation of a dimensionality reduction technique is inherent to SHM methodologies due to the large amount of handled data.8The use of dimensionality reduction techniques may enhance the performance of novelty detection algorithms by reducing the computational cost and unveiling hidden relationships among variables. The most widely used methods for dimensionality reduction rely on techniques based on orthogonal projections due to their simple geometric interpretation in a lower dimensional space; Principal Component Analysis (PCA)13and Factor Analysis (FA)14are two of the most common techniques into this group of methods.
Besides, other developments in dimensionality reduction techniques have been explored,like:Projection Pursuit,15Independent Component Analysis,16and Random Projections.17Among other nonlinear methods have been explored lately such as nonlinear-PCA,18Principal Curves,19Multidimensional Scaling,20Artificial Neural Networks (ANN),21and Genetic Algorithms for dimensionality reduction.22
Although machine learning algorithms for handling a large amount of information such as supervised and unsupervised pattern recognition may be part of an SHM methodology,the attention nowadays is focused on SHM-related applications with unsupervised pattern recognition due to its ability for novelty detection.8Unsupervised Artificial Neural Network for SHM works in a similar way as supervised ANN,but no prior knowledge about damage is required.3
Dervilis et al.23proposed a method based on Auto-Associative Neural Networks (AANN) using Radial Basis Function (RBF) where a statistical representation of training data using pristine information of a vibration analysis in a wind turbine blade structure was generated. Wen et al.24proposed a semi-supervised algorithm using ANN in order to classify operational conditions in an aircraft wing for a further damage localization under the premise of novelty detection.Palomino et al.25proposed a probabilistic neural network and fuzzy Gustafson-Kessel for clustering impedance signals in an aluminum panel; signals were gathered by piezoelectric patches, however the methodology presented drawbacks related to the location of the patches.
Self-Organized Maps(SOM),26are based in a topologically ordered mapping from signals in a neural network by regression; the map of features can be used as a part of a pattern recognition methodology. Xiao and Hu27presented an unsupervised pattern recognition algorithm combining upper and lower approximations in rough set spaces and SOM.An experiment with an aircraft actuator failure data was performed.This methodology is limited to discrete data set.
Sierra-Pe´rez et al.28developed a clustering visualization method based on SOM and PCA’s statistical tools Q and T2indices.Features were created applying PCA to the input data,therefore, an automatic clustering methodology DS2L-SOM was performed to classify the information. A novelty SOM parametric algorithm was developed by Abdeljaber et al.29,30.The SOM algorithm was implemented on a Phase II Experimental Benchmark Problem SHM data set,validated in a finite element method experiment. To generate the SOM topology,accelerometer signals were gathered under random excitation for damaged and undamaged conditions. The structure was equipped with 15 accelerometers. A numerical demonstration was made with five damage cases and 10 damage indices were computed. The algorithm showed a high sensitivity to damaged structures numerically simulated.
Deep learning algorithms are based on multilayer backpropagation algorithms commonly using Convolutional Neural Networks (CNNs). Each layer represents the information abstractly starting from the first level with a raw input of data.With enough number of layers and transformations, new and complex functions can be learned.31.
Although a large amount of studies has being developed under the supervised premise,unsupervised deep learning algorithms are in nowadays progress. Li et al.32presented a semisupervised deep learning algorithm called Augmented Deep Sparse Auto-Encoder (ADSAE), in order to assess pitting faults in gears; the rate of damage detection was around 99%. Sarkar et al.33evaluated crack damages on composite plates under bending training a Deep Auto-Encoder (DAE),using a visual abstraction method from experiments of plates without any crack and damaged plates; this methodology showed a high accuracy results.
Rosafalco et al.34conducted a study based on deep learning and Reduce Order Modeling.Data sets from a cantilever beam were gathered using a Reduced Basis method,this allowed to a Fully Convolutional Network algorithm to assess the structure’s condition. Cha et al.35proposed a semi-supervised deep architecture methodology using CNN for detecting cracks in concrete structures. A data-bank of cracks was created with a specific pixel size in order to train the nets. An interesting attribute of the algorithm is the absence of feature extraction techniques due to the fact that CNNs learns features automatically.The algorithm achieved a detection accuracy of 98.22%using 32000 images for training and validation. Other recent applications are presented by Refs. 36–38.
Unlike probabilistic algorithms, in the fuzzy clustering algorithms a feature can be simultaneously part of more than one cluster.Unsupervised fuzzy clustering is based on the optimization of a fuzzy objective function where a previous definition of the number of clusters ins not necessary. Here are included algorithms such as fuzzy C-means or fuzzy Kmeans, some health diagnostic algorithms have been used under this premise.
The article presented by Xu et al.39proposed an image matching recognition algorithm based on Possibility Fuzzy C-means(PFCM)kernel clustering.A two dimensional feature space was created and related using the Euclidean distance in the kernel space.By means of the Canny operator salient edges are defined and segmented using the PFCM clustering algorithm.Cano and da Silva40presented a strategy to detect operational conditions sensing lamb-waves in a CFRP structure under a variety of load conditions.With the purpose of revealing the operational conditions, prediction errors obtained by Auto-Regressive (AR) models were classified by means of a C-means algorithm. Mirsaeid and Hashemian41examined an unsupervised method with a fuzzy approach for structural applications, the algorithm consists in a K-means clustering algorithm with a fuzzy membership function.Operational conditions where detected using data from structural concrete samples.
The Gustafson-Kessel (GK) algorithms are based on fuzzy algorithms,however they were developed with the aim of having a better differentiation among classes. Dinh et al.42,43reported a GK clustering algorithm for detecting natural clusters using Acoustic Emission (AE) from a CFRP structure under fatigue loads.Ramasso et al.44also proposed an approximation of early detection of damage in a CFRP structure with AE using a GK algorithm, however, a clustering optimization procedure by means of probabilistic formulations was taken into consideration. Some other unsupervised methodologies includes evolving Gustafson-Kessel Possibilistic C-means clustering (eGKPCM),45Gustafson-Kessel fuzzy clustering algorithm based on the Deterministic Annealing approach (DAGK) algorithm46and an ensemble approach for a GK fuzzy clustering algorithm.47
Genetic Algorithms (GA) can be used for fitting quantitative models in addition to selecting parameters for optimizing the performance of a system or algorithm. In SHM, GA are also known as bio-inspired damage detection methods. A newly unsupervised method called Genetic Algorithm for Decision Boundary Analysis is presented by Silva et al.48; this algorithm was created for clustering optimization by a concentric hypersphere algorithm, as well as to develop a technique for characterization of clusters.
Betti et al.49associated a GA algorithm with ANN for structural damage identification.Meruane and Heylen50developed a methodology called Hybrid Real Coded Genetic Algorithm (Hybrid-RCGA) with the aim to detect structural conditions in aerospace frame structures. A damage penalization was convenient to determine a false alarm detection caused by noise, finally, results were compared with conventional methods.Other works include an Hybrid-GA clustering algorithm using a clustering validation criterion NK,51a high quality clustering using K-means and a GA algorithm with the intervention of fast hill-climbing cycles52and a hybrid genetic algorithm HG-means for minimum sum of squares clustering.53
Algorithms based on cost function optimization (Kmeans), are some of the most common unsupervised algorithms, however some input parameters must be set-up by hand such as the number of K-initial cluster centers. Nevertheless, K-means algorithms have been employed in the SHM framework for operational conditions clustering and damage detection. A damage sensing system presented by Diez et al.54employed a novelty unsupervised algorithm applied in the Sydney harbor bridge (Australia) for clustering a subgroup of joints with similar behavior. Tri-axial accelerometers collected vibration signals with the purpose of defining operational conditions.
Wang et al.55presented a flywheel fault detection using a data driven method which includes K-means and Ordering Points To Identify the Clustering Structure(OPTICS)for data classification of telemetry information in addition to a PCA algorithm to define relationships among parameters. Santos et al.56established a methodology to classify on-line different structural conditions in a bridge’s cable.Numerical and experimental data and real-time detection were reached by an ANN and K-means algorithm,the methodology was highly sensitive to different conditions. Al-Jumaili et al.57performed an unsupervised classification of transient AE signals from a CFRP structure buckling test by the implementation of a data reduction method by PCA and fuzzy C-means, then, K-means was used for unsupervised pattern recognition.
The algorithms presented above are noteworthy, however,the tune of parameters by hand and the computational complexity can be a drawback. Density based algorithms can find relationships in the space, connecting elements depending on the variation of the density among them with simple construction and low computational complexity.Density Based Spatial Clustering of Applications with Noise(DBSCAN),58Ordering Points To Identify the Clustering Structure (OPTICS)59and Density based Clustering (DENCLUE)60are well-known density clustering algorithms.
Javadian et al.61offered a semi-supervised fuzzy approach for a density-based algorithm called Fuzzy Unsupervised Active Learning Method (FUALM). Clustering is performed using a Connected-Components Labeling, which works as an ink-drop spread and expands from selected points forming clusters. Meng’Ao et al.62proposed a semi-supervised algorithm, which divides the data into grids and processes the information by means of DBSCAN, the grid process reduced distance computations of the parameter Eps.
Sharma and Rathi63contemplated an density based algorithm which avoids the input of parameters Eps and MinPts by the user. The Algorithm was called E-DBSCAN. Here the space is divided by cells, each cell defines a particular Eps and MinPts,therefore,those parameters are merged according to densities in each cell. Kumar and Reddy64developed a graph-based index structure method called Group, which accelerates the process of the neighbor search for DBSCAN in order to speed-up the clustering process.
Elbatta and Ashour65introduced an improved DBSCAN algorithm which detects clusters depending on the local density. The algorithm is called DMDBSCAN. this algorithm intends to find a suitable value of Eps for each density level found in the data set according to the K-dist plot from the K-nearest neighbor. Esmaelnejad et al.66suggested that the DBSCAN algorithm parameter Eps can be estimated using the noise ratio ρ of a specific data set. Minimum values of Eps that makes any point a core point are represented in a line chart.By means of this chart,a general value of Eps is defined using the precise value of ρ.Other works can be found in Refs.67–70.
The outline of this article implies a methodology for automatic operational conditions clustering in a structure considering an experiment developed in Ref. 71. The experiment included 32 Fiber Bragg Gratings (FBGs) bonded to the surface of an aluminum beam placed in cantilever under cyclic loads into 13 different pitch angles which became 13 different operational conditions and constituted the baseline data set.The aim of the experiment was the development of a machine learning technique based on a Local Density-based Simultaneous Two-Level Self-Organizing Maps(DS2L-SOM)algorithm capable of automatically inferring those 13 different operational conditions using strain signals gathered from the FBGs.
Although,the machine learning technique DS2L-SOM carried out by Ref. 71, was capable to determine such 13 variations into 12 different clusters in the aluminum beam’s experiment with high accuracy(two operation conditions were very similar to discriminate them as independent operational conditions), the computational cost was a drawback, since the aim should be to implement an on-line damage detection system in an Unmanned Aerial Vehicle (UAV). Thus, it was considered convenient to develop an alternative unsupervised clustering methodology with the ability of classifying unknown operational conditions using strain signals with low computational cost and reliable accuracy which could be part of a future SHM methodology for damage detection designed to avoid these drawbacks.
In consequence a pipeline algorithm to infer specific operational conditions in a sample structure using the baseline data set is presented in this work. In a first stage, a dimensionality reduction technique was performed to the beam’s data set using factor analysis. It was possible to determine hidden features using two common factors which represent the baseline data set in a lower dimensional space.Further,the FA performance for dimensionality reduction was evaluated.
In a second stage, a density based clustering algorithm DBSCAN was used to automatically classify the beam’s data set (baseline data set) with the aim of inferring the 13 operational conditions without having previous knowledge of them.DBSCAN’s input parameters were automatized by the use of a Genetic Algorithm.The computational cost and precision was determined, and a comparative study with the DS2L-SOM clustering methodology developed by Ref. 71 was included.
2. Strain field pattern recognition
The greatest challenge in an SHM process is a suitable damage detection method.However,before defining what is considered damage and until which point this damage is allowable, it has to be defined under which conditions the structure is considered pristine. Damage detection depends on system’s particularities, e.g. if the structure is thought as a critical structure where lives and high costs are involved or if is considered as a safe life structure where a particular damage is considered allowable for a period of time and/or number of cycles.
When a structure is submitted to loads derived from its regular operation,it will always be related to a strain field and this may vary in order to a change in the imposed loads,nevertheless, the strain field may also vary as consequence of damage occurrence. This situation can be extrapolated to an aircraft structure under regular operational conditions which will be subjected to variety of loads. Structural loads under regular operational conditions are expected to be admissible under the structural operating limits of the aircraft such as the V-n diagram,however,although it is expected that the structure remains pristine under these load conditions, an specific relationship between the strain field and loads for the pristine conditions is a structural state that is nearly unknown.
The baseline modeling is the process where the relationships among some sensitive features (such as the strain field) and loads from pristine conditions are determined, this is developed by gathering data from the pristine structure under regular operational conditions, and from this, a baseline model is created. The drawback relies on how pristine conditions are identified when loads do not have a specific magnitude (as it may happen in an aircraft flying under regular conditions),where loads are unexpected and are not clearly defined.
Here is where the use of an unsupervised pattern recognition algorithm such the pipeline presented here takes importance since it can be used in an exploratory analysis where classes related to the pristine (undamaged) conditions are not clearly defined in Ref. 72, see Fig. 1.
As a following step which is out of scope of this work,damage detection can be performed by projecting new gathered data from unknown conditions into each one of such models built in the baseline modeling. Several confidence intervals such as scores and indices are desired for this process in order to define which of this new information is considered as an anomaly or a damage indication.73One of the axioms developed by Worden et al.74which states that ‘‘the assessment of damage requires a comparison between two system states”,relates the data projection process for damage detection. See Fig. 2.
The strain field of a structure can be determined through strain measurements gathered by means of a specific array of sensors e.g.FBGs or strain gauges,attached or embedded into or to the structure,with the ability to register damage-sensitive features,strain in this case,via on-line(real time)or off-line as it is presented in the Section 3.
3. Fiber bragg gratings
A way to measure strain or thermal variations in a structure is through the use of a particular kind of FOS called Fiber Bragg Gratings (FBGs). These have several operational advantages as electrically passive operation, great sensitivity, electromagnetic interference invulnerability and multiplexing capacity for hundred of sensors along a single fiber. Basically, when the light passes through an FBG, a proportional part of the Bragg’s wavelength is reflected back.The reflected wavelength varies proportionally to the deformation of the FBG which is bonded to or embedded into a structure. The Bragg’s wavelength is given by the Eq. (1), presented in Ref. 75:
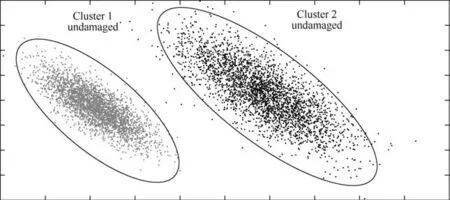
Fig. 1 Representation of a Baseline modeling defined using an unsupervised pattern recognition algorithm.

Fig. 2 Representation of a damage detection by projecting new information into baseline.

where n is the effective refractive index of the fiber’s core and Λ is the grating’s pitch.The relation between strain,temperature and Bragg’s wavelength is given by:

where the fiber photo-elastic coefficient of the FBG is represented by ραand ξ represents the thermo-optic coefficient of the fiber.
The values for strain and temperature variation as function of wavelength were experimentally obtained by Sierra-Pe´rez et al.76and are presented as follows:

4. Feature extraction
With the aim to enhance the clustering performance and the quality of results, the application of preliminary processing techniques (preprocessing) is needed. Signal noise which has a high frequency nature and redundancies are intended to be avoided, this undesired information can be stored unnecessarily increasing the data size and the computational cost. Further, outliers which also are undesired, can be presented due to human manipulation or sensing system failures. Thus, not every signal recorded may be considered meaningful for the clustering process.
As it was found experimentally in Ref. 71, for a suitable selection of significant strain signals, a Signal to Noise Ratio(SNR) over 50 may improve the overall classification process,since, if the strain signal magnitude is close to the white noise of the acquisition equipment, patterns are faded by the white nose with a Gaussian nature. Therefore, for the used Micron Optics interrogator (SM130), which has a white noise around±1με, magnitudes over 50με were desired.
Furthermore, in many cases, different magnitudes and scales may be involved in the data acquisition process (e.g.strain, temperature, pressure, etc). The action of scaling data allows to avoid differences that are not relevant in the classification process; using the auto-scaling process each variable is re-scaled to have zero mean and unity variance. Following the notation of Mujica et al.,77each measurement (row vector) from all sensor in a time instant is represented by xi, further, each column or sensor vector vjof the matrix is redefined by:

where μvjrepresents the mean of a sensor vjmeasurements and is given by:

Through a dimensionality reduction method, it is possible to describe a large quantity of the original information in a new low-dimensional space.
Despite the well known technique Principal Component Analysis or PCA has probe to be a simple and efficient dimensionality reduction technique, FA was selected to perform the dimensionality reduction process due to it can reveal unique and underlying structures from the original data set which PCA is not able to reveal.78FA is also a linear method like traditional PCA.79
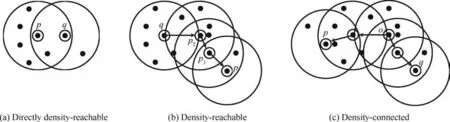
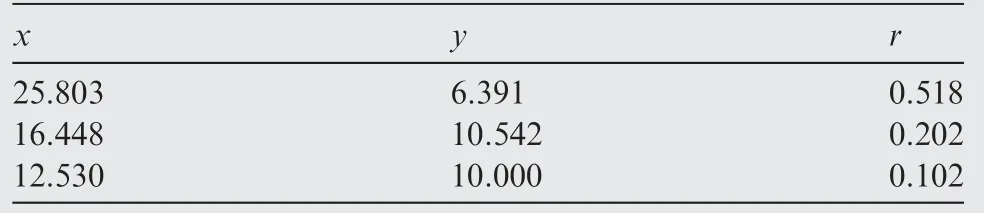
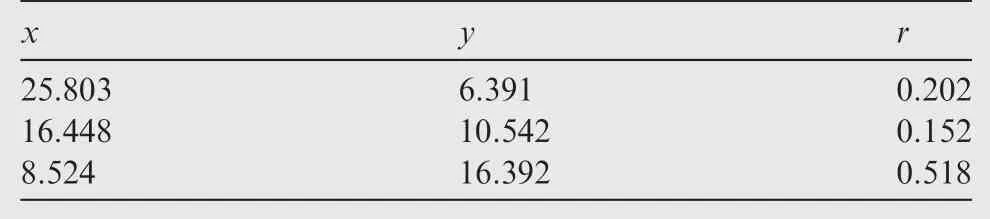
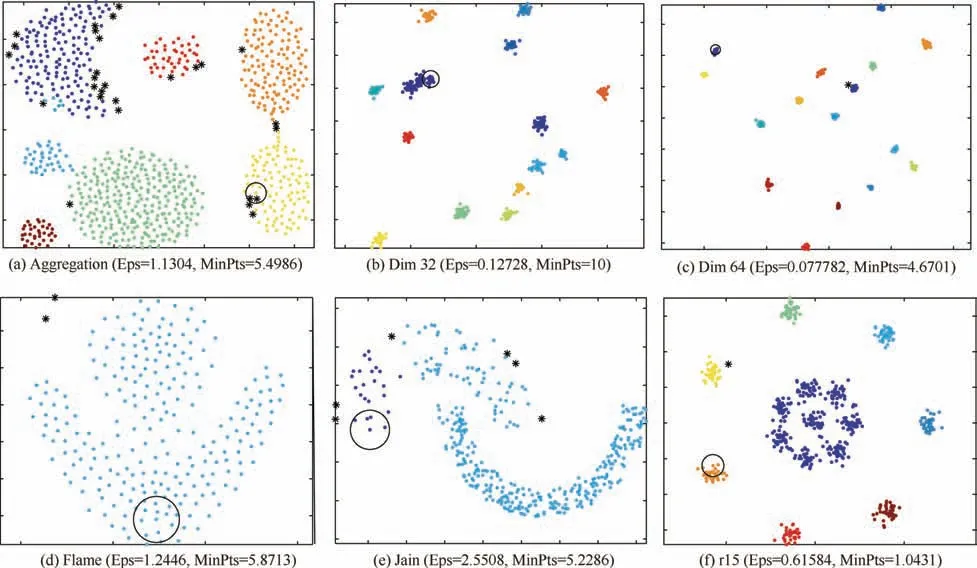
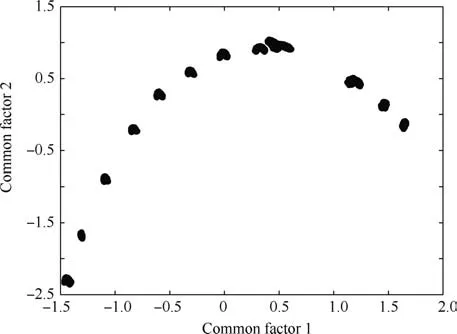
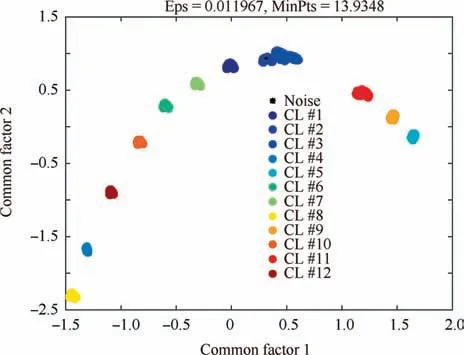
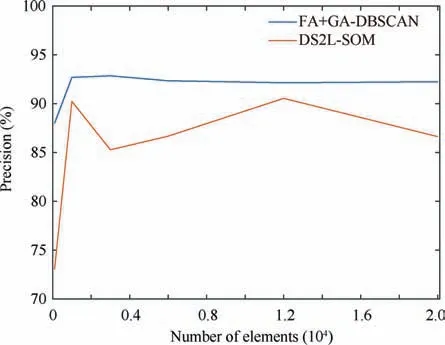
The main goal of FA is to describe how the original xijvariables in a data set depend on a small number of variables k with k The general equation form of FA is presented: FA model can be represented in terms of covariances according to: where Σ is the data covariance matrix, and Ψ the covariance matrix of the specific factors. Assuming T as an orthogonal matrix, Γ and Ψ are calculated using Γ*=ΓT as follows: By selecting some restrictions for Γ it can be found an initial unique solution. Therefore by multiplying the orthogonal matrix T times the initial solution, other solutions can be found as Γ is rotated until a particular ‘‘best” solution is found. Using multivariate normality of f and e, the values of Ψ and Γ can be estimated by maximum likelihood by an iterative process as explained in Ref. 14. Varimax,82quartimax83and promax84are common rotation matrices used by mostly FA algorithms.81The most important variation among the rotation matrices implies the fact that the projections may be orthogonal or oblique.Selecting a number of factors desired to rotate will reduce the dimensionality of the original data set. In consequence, there is a number of eigenvalues which describe the information retained, related to the selected number of factors. There are several rules to determining the amount of factors necessary to describe a reliable quantity of the original information. The most common method is the so called ‘‘eigenvalues greater than one rule”presented in Ref.85.The idea of this rule is retaining the factors with eigenvalues greater than one,these factors may perform the best description of the original samples. Other rules also included in PCA, are focused on keeping the factors in which the cumulative variance describes more than the 80% of the original variance.85In addition, there is also a graphic method called the‘‘scree plot”in which the factors before the breaking point have to be retained. The aim with the presented dimensionality reduction technique is to group the common factors that keep a relation among variables, since further, it is necessary to cluster the common factors using a density based algorithm which is desired to work in a two-dimensional space to keep the computational cost as low as possible.Thus,it is desired to retain two common factors.Besides reducing the computational cost,in a two dimensional space it is possible to graphically represent the formed clusters in order to validate in a graphic way the performance of the developed pipeline algorithm. It is expected that ‘‘new variables” be related in between due to the preservation of the difference in magnitude among signals in a lower space, and in consequence, a large quantity of the original information can be described. Therefore, those signals represented in a new dimensional space by the common factors should fall in a same cluster. Following the Mujica et al.77notation, the original data set D is a matrix of size Dm×n, with m time instants or experimental trials and n variables (sensors). When FA is applied to the data matrix, the data set can be represented in a lower dimension of size Dm×2by selecting the first two common factors, see Fig. 3. Each row of the new matrix will result in a point ofcoordinates that can be represented graphically and clustered. The DBSCAN clustering algorithm, is an unsupervised algorithm created by Ester et al.58The criteria for DBSCAN algorithm selection was based on its ability to determine clusters without predefined class labels. DBSCAN often offers a superior performance than well known techniques such as K-means or hierarchical algorithms given that, it is not necessary to determine the number of desired clusters a priori. DBSCAN tuning parameters are minimal since it was designed to perform an unsupervised clustering as an exploratory search for features in large data sets;besides,it was developed to keep a low computational cost with a time cost ofand O(n2) in the worst scenario.86 Fig. 3 Dimensionality reduction projection using common factors of factor analysis. DBSCAN works detecting a common density of points in a two-dimensional Euclidean space(in this case the dimensionality reduced data set Dm×2). It is considered that such density will be greater with points related in between than in surrounded zones out of a cluster. DBSCAN selects a random point and measures the distance among it and random surrounding points and a next point, and so on successively with all other points. The algorithm correlates the points belonging to the data set depending on the initial parameters configuration Eps and MinPts. The value of Eps and MinPts have to be designated as input parameters. The Eps input parameter manages a circle radius in which a specific density is desired, and the MinPts parameter determines a minimum number of points desired in the circle. Following the original notation presented in Ref. 58,DBSCAN algorithm follows six basics rules for clustering a data set Dm×2: Deliberate selection of the initial input parameters Eps and MinPts, becomes the classification algorithm less ‘‘automatized”; besides, the performance and accuracy of clustering can substantially decrease. Automatizing the selection of the input parameters may avoid the seeking of values by trialand-error. Thus, a strategy with the aim to select the DBSCAN’s initial parameters depending on the scatter and the space location of the points was developed. Gaonkar presented one of those efforts to improve the automatism of the DBSCAN algorithm.87In his article a technique to automatically determine the parameter Eps was evaluated.However,the author proposed a brief way to determine the parameter MinPts; nevertheless, in the methodology presented in this work,the determination of the parameter MinPts was slightly altered having in mind that some changes drove better results. The machine learning function nearest neighbor,allows discovering distances using the Euclidean distance among a selected point and the leftover points in a specific data set D;this function also may defines the densities contained in the specific data set D.Therefore,those values may become possible Eps values. Those values are also treated further in Section 5.3 as a part of the methodology to chose the best Eps value. The selection of MinPts is represented by: where diis the i-th value of each density measured in the neighborhood of a point content in a specific data set D with n number of experiments. Fig. 4 Directly density-reachable, density-reachable, and density-connected. In the methodology presented in this work, a GA was implemented to enhance the performance of DBSCAN by automatic definition of the parameter Eps for a specific data set D.GA is a technique developed for optimization, it simulates the natural evolution allowing a population of a particular number of individuals to evolve in a specific form under a variety of conditions or rules to a state that maximizes or minimizes a fitness function.88In other words,the main goal is to reach the specific solution through a fitness value. The parameter Eps has a large influence over the performance of the DBSCAN algorithm since it has a direct relationship with the typical density of the data set. Determining an adequate Eps value for a specific data set could significantly increases the automation process, accuracy and reduces processing time. In this work DBSCAN was automatized by a GA based on the scheme presented in Ref. 89. The initial population of the GA was determined using the nearest neighbor function. Those distances can be defined as the most common radii associated to a specific data set D,therefore the initial population was set up with 50 radii between the average radius ravgand the maximum radius rmax. The chromosomes of the initial population (solutions) had two different genes,one gene was composed by a point pifrom the common factors data set Dm×2with x,y coordinates and the other one had a radius rifound using the nearest neighbor function. Hence, the chromosome could be a combination of real numbers as it is represented in Table 1. The fitness function was defined by using three variables(CR, SD and DR) according to: where the Coverage Ratio (CR) is given by: Sum of Density (SD) is given by: and Duplicate Ratio (DR) is given by: Each Spi,rirepresent a set of points with center piradius ri. Radii with maximum values were selected, including their belonging points and avoiding redundant points,this is known as the tournament method. In this methodology, half of the initial chromosomes were replaced after each sample was evaluated with the Fitness Function. For better comprehension,replaced positions can be identified by the bold text. Table 1 A general chromosome scheme. The crossover process consists in the selection of random fraction of elements belonging to a chromosome and performing an exchange of those elements among selected chromosomes. The population before crossover is presented in Table 2. In a subsequent step, the process was made by fixing the point coordinates and randomly varying radii positions.The new chromosomes with best fitting are shown in Table 3. Some chromosomes can be exposed to a mutation. The mutation consists in changing a fraction of elements belonging to a chromosome with new information randomly selected from a specific population. The mutation process was carried out by replacing radii values from some selected chromosomes with new ones in random positions,the new radii values can be larger than the maximum value of the initial population but not lesser than the lower value. In the same way, points with center piwere replaced with new values in random positions.An example of the mutation process is indicated in Table 4.In the mutation not every chromosome was modified, some of them just changed the radius or the point pibelonging to the initial population. A new family of chromosomes were obtained after the processes aforementioned to the genetic algorithm and were evaluated over and over again using the fitness function with the aim to improve the information inside each chromosome until a solution converged.In this case,100 iterations of the sequential process were necessary to guarantee a rate of convergence of 0.01%. Finally, the best radii selected by the GA could be used as the best suited Eps for a specific data set D.Moreover,with the use of the automatically selected Eps,the DBSCAN algorithm will perform a more accurate and faster clustering. To validate the genetic-DBSCAN algorithm,six different data sets were used; these are free access artificial data sets, which are specially designed with the aim of testing pattern recognition algorithms under development.Data sets are available online at Ref. 90. The overall precision was evaluated using the Eq.(17),proposed in Ref. 91; where TP are the true positives or hit rate and FP the false positive or false alarm rate. TP and FP can be calculated using: Table 2 Population before crossover. Table 3 Population after crossover. Table 4 GA after mutation. Well condensed data sets such as ‘‘Dim 32”, ‘‘Dim 64”,92and‘‘Aggregation”93reveal a fine outcome from the automatic processing of the algorithm with higher precision level; otherwise,‘‘Flame”,94‘‘r15”95and‘‘Jain”96data sets,due their fuzzy nature, represent a limitation for the algorithm, where the algorithm’s precision decreases considerably. See Fig. 5. Clustering results are condensed in Table 5 including the overall precision. For the purpose of evaluating the present methodology, an experiment carried out in Ref.97 was taken into consideration,a general description of the experiment is presented in Fig. 6(a). A hollow squared shape aluminum beam with a 20mm×40mm cross section, 1mm thickness, and a free cantilever length of 1200mm, was considered to represent a system’s main structure such as an aircraft wing’s main spar or a wind turbine blade’s main spar. See Fig. 6(c). The clamping zone(which was fixed to a testing workbench frame using‘‘C–clamps”) was filled with a wooden core to prevent plastic deformations. The beam was submitted to dynamic bending loads using a constant amplitude displacement at the beam’s tip, with an electric motor coupled to the beam with a connecting rod at a frequency around 4Hz. The maximum deflection at the beam’s tip was around 14mm.13 different experiments were carried out; the experimental evaluation included 13 different pitch angles (positions) with an angle variation of 2°among experiments in order to generate data between -8°and 16°.The beam was loaded under a P load which promotes a deflection δ, See Fig. 7. A pitch angle indicator was placed in a side of the beam to have control on the pitch shift between experiments. In each experiment the beam was cycled 410s. The idea of changing the pitch angle was to emulate an aerospace structure under variable load conditions similar to those which occur during the normal operation. Four fiber optic lines were bonded on the surface of the aluminum beam, each one having eight FBGs. In total 32 FBGs were bonded parallel to the beam’s longitudinal axis (x axis);31 FBGs for strain measurements and one for thermal compensation (mechanically isolated). The first group of FBGs were placed at 50mm from the clamping zone, the rest were placed with a spacing of 150mm between them. Each FBG had length of 2mm and wavelengths between 1510nm and 1590nm. Detailed views of the FBGs distribution are presented in Fig. 6(b) and (d). Fig. 5 Artificial data set clustering results. Table 5 Artificial data sets validation results. Fig. 6 Experimental setup overview, sensors distribution, aluminum beam’s cross section, sensors distribution measurement. The acquisition system consisted in a four-channel Micron Optics SM130 optical fiber interrogator. Strains were measured at a sampling rate of 100Hz. Each experiment was carried out twice, in order to generate validation data and the baseline data set. Furthermore, computational processing was performed in a (Intel Core i7, 2.2GHz processor, 6GB of RAM and 500GB hard drive) PC, algorithms were run in MATLAB R2014a, in a Windows 7 PC. To assure a change in the strain field, the beam in cantilever was placed in a certain number of pitch angles under bending loads. As it is stated by the beam’s theory, a variation in the section inertia promoted by changes in pitch angle change the global beam’s stiffness (deflection, which denotes stiffness,is inversely proportional to inertia). Further, as can be seen in the Eq.(20),the beam’s stiffness can be considered as the combination of the Young’s modulus (material stiffness) and the moment of inertia (cross-sectional stiffness). where P is the bending load, L the beams’s length (cantilever length),E the Young’s modulus,and Ixxthe moment of inertia of the cross-sectional area.It was expected that,for every pitch angle the stiffness varies in such way that it can be detected by the algorithm as a specific operational condition related to a unique strain field. As it is presented in Fig. 8, where some of the pitch angles are represented graphically in a strain vs strain plot using data from two different sensors belonging to the experimental setup, a nonlinear trend was evident. However, the information can be adjusted linearly by a dimensionality reduction model decreasing the computational cost of the overall process, taking into account that, in some cases the loss of information could be meaningless. Those strain measurements represented graphically above,may be an insinuation of a class in a further dimensionality reduction and classification process. Each pitch angle was represented by the most significant data after the preliminary processing described in Section 4. Here,the physical phenomena that governs the experiment (beam defection), can be simplified to a state of tension/compression in the opposite faces parallel to the principal axis.The selection of discretized maximum and minimum signal peaks and peaks vicinity points that represent the state of maximum tension/-compression loads also avoided outliers and noise. Fig. 7 Beam’s cross section pitch angle variation. All matrices (corresponding to all pitch angles) were concatenated in a single matrix called baseline matrix Dm×n. Each row m in the baseline matrix was randomly arranged with the aim to recreate a real case scenario in which unknown load magnitudes appear arbitrarily. As a result, a matrix with 20935 experimental trials belonging to each pitch angle and 31 sensors was created; the size of the matrix was determined as D20935×31. As it was mentioned above, the dimensionality reduction technique was performed projecting those 31 dimensions in a low-dimensional space. After performing the factor analysis process, a matrix of D20935×2was obtained retaining two common factors, see Fig. 9. The Promax projection, which is an oblique method,was selected for the dimensionality reduction given that it is able to perform a most balanced projection of the original information with only two common factors retained.As consequence, it could be easier to interpret. Besides, it was evident that performing this projection resulted in well-separated and condensed groups that could contain the strain pattern related to a particular operational condition (pitch angle). It was just necessary to retain two common factors to describe the 99.23% of the original information. The first two common factors had a eigenvalue greater than 1,the common factor 1 had an eigenvalue of 25.277 and the common factor 2 an eigenvalue of 5.485.Therefore,the rules established to determine the performance of the dimensionality reduction technique were followed. Fig. 8 Example of Strain vs. Strain plot for pitch angles θ from-8° to 6° which represents change in local stiffness (strain field)between sensor 1 and sensor 2. The clustering methodology was tested using the experimental data set (dimensionality reduced aluminum beam’s data set D20935×2). The parameter MinPts=13.9348 was found using the corresponding equation presented in Section 5.2 and the parameter Eps=0.011967 was defined automatically by the genetic algorithm presented in Section 5.3. The algorithm was able to find 12 clusters,from 13 original classes belonging to 13 pitch angles. A total of 20932 points were clustered into 12 different clusters and 3 points were identified as noise.Each formed cluster can be identified in a specific color scale in Fig.10.Only the first two common factors of the aluminum beam’s data set were used. Each cluster of points(CL)is represented graphically by a specific color,Noise points are represented by asterisks. The beam’s stiffness can be considered as the combination of the Young’s modulus and the moment of inertia. For some pitch angles there was a loose in stiffness due a reduction in the moment of inertia induced by the rotation of the transverse section. Therefore, due to the previous conditions (discrete stiffness changes),a group of well-defined clusters was detected by the algorithm. Fig. 9 Factor analysis dimensionality reduction using the first two common factors from the aluminum beam’s data set. In order to summarize the overall pipeline methodology presented in this work, it was named as FA+GA-DBSCAN.The intention of this Section is to contrast the performance and computational cost between the developed methodology and a well proven methodology named DS2L-SOM proposed by Sierra-Pe´rez,71taking into account the aluminum’s beam data set explained in Section 6. This comparison allowed to have a benchmark for the performance of the FA+GA-DBSCAN considering that the algorithm presented by Sierra-Pe´rez derived reliable results.This comparison was carried out using two common methods for algorithm classification assessment such as the confusion matrix and the Receiver Operating Characteristic (ROC)curves presented in Section 7.4.1 and Section 7.4.3. The comparison was performed using MATLAB R2014a for Windows 10 in an Intel Core i7 with an 2.6GHz processor and 16GB of RAM. Both algorithms were run for the same data set(aluminum’s beam data set),using subsets with different sizes. Each algorithm was run ten times for each subset in order to study the repeatability and/or to identify trends related to compilation anomalies. As a result,both algorithms seemed to perform a stable and fast clustering,leading to similar results.However,the computational cost had a notable difference between algorithms. It was evident that the FA+GA-DBSCAN achieved the best computational cost. The average computational cost of the DS2L-SOM with 20000 elements was 32.923s almost twice in comparison with the FA+GA-DBSCAN which had an average processing time of 20.324s, see Fig. 11. It is important to remark that DBSCAN algorithm computational cost increases aswhile SOM based algorithm computational cost increases as O(n2)98; this can explain the computational time reduction achieved. However,the selection of accurate initial parameters, in which the function nearest neighbor is involved, could reduce the computational cost of the overall process to, where d is the maximum number of distance computations related to the function nearest neighbor as it was stated by Ref. 64 in a similar approach. Fig. 10 Clustering results by using FA+GA-DBSCAN pipeline algorithm and definition of parameters Eps and MinPts. 7.4.1. Determination of precision using the confusion matrix method The main objective of the confusion matrix is to determine a correlation between the clusters found by the classification algorithm and the original groups. The precision of the FA+GA-DBSCAN was determined with the use of a confusion matrix. The correlation of each original measurement with a clustered point was defined into it. Six data subsets were defined to determine the precision and Area Under Curve (AUC) from the ROC graph. The subsets consisted of 100, 1000, 3000, 12000 and 20000 trials from the baseline data set. The overall performance of the FA+GADBSCAN and the DS2L-SOM were notable,both with a precision close to 90%.The precision of the FA+GA-DBSCAN was slightly better and more consistent than the DS2L-SOM as it is shown in Fig. 12. The precision was calculated with the Eq. (17) presented in Section 5.4. Two characteristics may explain the differences between the precision of the algorithms, the first one related to the DS2LSOM precision detriment associated with the initial weights of its neural networks which is defined randomly. On the other hand, the FA+GA-DBSCAN is a classifier with crisp properties,given that,the algorithm will have a better performance with well defined and condensed data sets, however, it precision will decrease with fuzzy data sets. The cause of FA+GA-DBSCAN algorithm precision reduction with the complete baseline data set is related to the Cluster Number 9(CL9).This cluster contains strain measurements for two specific classes (pitch angles): 8°and 10°.This phenomenon appeared to be similar in both algorithms.These two original pitch angles were not as mechanically different as expected,and the inferred strain field could have been very similar and therefore, The classifiers were not able to determine a difference between classes. Fig. 11 FA+GA-DBSCAN and DS2L-SOM overall time complexity with standard deviation comparison using the baseline subsets. Fig. 12 FA+GA-DBSCAN and DS2L-SOM overall precision comparison using baseline data subsets. 7.4.2. Recall and F-measure Recall represents the effectiveness of the algorithm, recall is defined as the ratio of correctly classified (true positives) samples and misclassified samples(false negatives),this measure is defined by: where TP are the true positives or hit rate and FN the false negative. Moreover, F-measure or F1-score defined by Eq. (22), is a well known performance metric based on the Dice coefficient,it measures the harmonic mean of precision and recall.99F1-score benefits algorithms with higher sensitivity,100however it is a good way to evaluate the classifier’s performance. F1-score of FA+GA-DBSCAN and DS2L-SOM were measured taking into account the baseline data subsets presented in Section 7.4.1. Fig. 13 FA+GA-DBSCAN and DS2L-SOM Recall comparison using baseline data subsets. As shown in Fig.13,the FA+GA-DBSCAN has a better performance than the one shown by the DS2L-SOM detecting a large amount of true positives irrespective of the number of elements.This is related to the initiation of random weights in the DS2L-SOM algorithm, thus, certain information was defined as false negative. Conversely, the FA+GADBSCAN parameters (MinPts and Eps), are defined by an optimization process, as consequence, a maximum value for the parameter Eps is obtained. If the optimization process is performed in a properly way,the results for different runs will not vary significantly. In addition, Fig. 14 shows the results for the F1-score,where the higher the score represents the better relationship between recall and precision. Again, FA+GA-DBSCAN exhibited a stable behavior around 95%for every defined subset.On the other hand,the DS2L-SOM algorithm,displayed a performance reduction in the F1-score metric as far as the number of elements increases. The reduction in the F1-score represents a worse performance for clustering imbalanced data sets.101 7.4.3. Receiver operating characteristic curves Over the last years,ROC curves have had an increase on their application to determine the classifiers’performance due to the lack of proper and simple metrics.96Mainly,the ROC analysis can be a guide to determine graphically,the precision of a classifier for a specific problem. The classifier performance can be determined identifying how many data points are clustered as true positives, if the sample is positive and it is clustered as positive and false positives, if the sample is positive and it is clustered as negative. The classification capability of the algorithm can be determined visualizing the Area Under the Curve AUC in the ROC curve. To understand the capability of the classifier, it is necessary to represent graphically the ROC space using the true positives (tp rate) for the y axis vs. the false positives(fp rate)for the x axis and determine the area under this curve.As presented by Ref. 96, the classification algorithms achieve their highest accuracy if the AUC remains around 70%. Fig. 14 FA+GA-DBSCAN and DS2L-SOM F1-score comparison using baseline data subsets. Fig. 15 FA+GA-DBSCAN and DS2L-SOM AUC comparison using baseline subsets. There were used the same subsets of the Section 7.4.1 for this purpose. in this particular case the AUC of the DS2LSOM and the FA+GA-DBSCAN algorithm remains around 70%,however,the AUC FA+GA-DBSCAN is slightly superior.Hence,the FA+GA-DBSCAN algorithm was not overtrained, and the results obtained so far by the methodology were reliable. The results are presented in Fig. 15. This work tried out a fast and precise pipeline machine learning methodology proposed for automatic operational condition identification in the framework of the SHM. To complete the proposed methodology, an experiment carried out by Sierra-Pe´rez71was considered. The experiment consisted in an aluminum beam instrumented with FBGs placed in cantilever under dynamic loads in 13 different operational conditions. A variety of algorithms belonging to the field of machine learning were taken into account. A system evaluation and a preliminary process were performed to remove outliers. The use of an accurate preliminary process technique in relation to the physical phenomena enhanced the clustering performance, since it generated clearer groups and remove unnecessary information. A dimensionality reduction technique called factor analysis was explored to perform a dimensionality reduction of the beam’s baseline data. The beam’s data were projected in a two-dimensional space for a further clustering process. The FA technique seemed to have a solid ability to match specific loads with strain signals in a environment were unexpected loads can suddenly appear. FA can be considered as an alternative for PCA in the dimensionality reduction process,in which its properties can be explored for handling information in multidimensional data sets. A clustering algorithm called DBSCAN was used for grouping the reduced information from the FA process. The machine learning function nearest neighbor was meaningful in the initial parameters MinPts and Eps determination. Further, the DBSCAN algorithm was automatized with a genetic algorithm looking for determining the initial parameter Eps.The handling of a genetic algorithm improved the DBSCAN capabilities substantially; due to the automation of the DBSCAN with a GA,it was possible to infer a variety of structural operational conditions presented in an experimental procedure with an aluminum beam given by the effect of different pitch angle configurations. A total of 12 different operational conditions were identified in an unsupervised way.The experimental results lay bare that due to the action of the genetic algorithm the selection of an automatized MinPts lead to specific clusters that could have been optimum in size,rejecting specific signals as outliers since DBSCAN is also capable of detecting noise. Under this terms,the algorithm had an overall precision over 90%.In the same way, a comparison made with a well-proven methodology, left clear that the computational cost of the FA+GA-DBSCAN was satisfactory, reducing almost in a half the processing time. As it was presented above,FA+GA-DBSCAN algorithm had more sensitivity for clustering detection in condensed data sets,and a loss of accuracy was identified when fuzzy data sets were handled.Hence,it is suggested to perform a data set clustering in such way that the data sets remain in the most condensed form possible. Further, the stiffness of a structure in cantilever submitted under dynamic loads was an underlying factor in the methodology for the dimensionality reduction and strain signal data classification processes. Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgements This work was supported by the Centro de Investigacio´n para el Desarrollo y la Innovacio´n(CIDI)from Universidad Pontificia Bolivariana (No. 636B-06/16–57).



5. DBSCAN clustering
5.1. DBSCAN


5.2. Definition of MinPts

5.3. Definition of Eps using a genetic algorithm





5.4. Clustering validation



6. Experimental setup


7. Results and analysis
7.1. System evaluation

7.2. Preliminary processing


7.3. Strain signals clustering
7.4. Precision and performance






8. Conclusions
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Recent active thermal management technologies for the development of energy-optimized aerospace vehicles in China
- Electrochemical machining of complex components of aero-engines: Developments, trends, and technological advances
- Recent progress of residual stress measurement methods: A review
- Micromanufacturing technologies of compact heat exchangers for hypersonic precooled airbreathing propulsion: A review
- Towards intelligent design optimization: Progress and challenge of design optimization theories and technologies for plastic forming
- A combined technique of Kalman filter, artificial neural network and fuzzy logic for gas turbines and signal fault isolation
