涡漩对迷宫流道灌水器水流流态的数值影响分析

马炎超

（太原市城乡管理局，太原030002）

0 引 言

灌水器作为滴灌系统中核心部件，其使用寿命主要受堵塞程度因素的制约[1]。在实际农田灌溉中，正常使用2 a 左右后，滴管灌水器会产生不同程度的堵塞现象。即使通过完善的过滤措施让进入灌水器内的水保持良好的水质，灌水器内仍会出现近33%的物理堵塞现象[2]。

为进一步分析灌水器的堵塞程度，众多研究人员主要针对迷宫流道中的漩涡与抗堵塞性能展开探索与研究。王尚锦等[3]以圆弧式迷宫流道为研究对象，从流道内的水流流动特性着手研究，结果表明流道内存在的涡旋有利于提高灌水器内的抗堵塞性。魏正英等[4]认为迷宫流道内的堵塞现象主要是由于流体中所夹带的微小颗粒在流动滞止区沉积所致，并采用了优化灌水器迷宫流道主航道的设计方法来提高其抗堵性能。张琴等[5]通过对矩形迷宫灌水器内水流流线分布情况进行数值模拟，并根据流线变化将流道内的速度涡旋区和低速滞止区去除，设计出了抗堵性能优越的圆弧形流道结构。康苗业等[6]以流道内内齿的相对位置、间距及高度为参变量来探求双内齿形灌水器的抗堵性及水力性能。李嘉露等[7]以流道结构参数与流态指数为控制因素，通过2者间的回归模型为改进型双向流流道结构优化提供一定的理论参考。杨彬等[8]通过数值模拟与物理试验相结合的方案分析了齿形迷宫流道灌水器结构参数变化对水力性能的互馈影响。麻江峰等[9]认为三角形迷宫灌水器在去掉漩涡后可显著提高其水力性能。崔振华等[10]应用Fluent软件模拟分析了滴灌灌水器弧形迷宫流道在不同压力水头下流道内速度流场变化规律及弧高、齿间参变量等结构参数与水力性能的变化关系。郭霖等[11]利用数值模拟计算和多元线性回归分析的方法，得到了三角形流道内各结构参变量、水流流量系数和流态指数之间的定量关系。为能够对弧形迷宫灌水器的结构设计提供理论支撑，武鹏等[12]针对弧形和弧齿形2种流道结构内颗粒的运动状态及对抗堵性能的影响进行了研究。ADIN 等[13]通过实验研究发现，对灌水器流道结构进行优化后，可以有效地减少颗粒的沉积，提高流道内抗堵性能。王建东等[14]比较了不同滴头内水流抗堵塞性能与其流道长度、断面面积及水流流态指数之间的关系，以滴头流量、流道长度及水头压力为参变量，建立多元线性回归模型。常莹华[15]等认为灌水器流道内剧烈的涡旋运动有助于提高其抗堵塞性及消能作用。

综上所述，流道形式、结构参变量的差异会引起灌水器内部水流涡漩的重新分布、进而影响其水力性能及抗堵性能，通过多元线性回归模型，可直观地反映出水流流量系数、流态指数及各流道参变量的定量关系。因此，涡漩的存在显著影响着迷宫流道灌水器内水流流态、水力性能及其抗堵性能。但目前以涡漩为参变量，来研究其对常规形式的迷宫流道灌水器内各水力参数的数值影响却鲜有报道。通过数值模拟计算分析，对三角形、矩形、齿形、梯形4种形式的灌水器流道在不同压力水头下的水流流场进行研究，根据模拟出的水流流线变化，尽可能地去除流道内拐弯处及转角边壁处的旋涡，得出圆弧形无涡流道结构模型，并定量分析了其水流流态分布变化。在此基础上，比较了有涡和无涡流道的水力性能，旨在探求迷宫灌水器流道内涡漩的存在对灌水器水力性能影响的根本原因，为性能优越的迷宫灌水器研制提供更进一步理论基础。

1 迷宫灌水器模型及网格划分

1.1 流道结构

选取矩形、齿形、三角形、梯形4种基本形式的流道结构迷宫灌水器模型。其流道总长均为340 mm，其中三角形灌水器流道单元200 个，矩形灌水器流道单元85 个，齿形灌水器流道单元121 个，梯形流道单元170 个。由于迷宫灌水器水力现象在单元上具有重复性，4种基本形式迷宫灌水器按实际尺寸进行建模时，矩形选取3 个流道单元，齿形6 个流道单元，梯形4 个流道单元，三角形7 个流道单元进行建模，其迷宫灌水器流道尺寸参数见表1。

各形式流道平面结构单元中箭头方向指向为水流流动方向。4种三维立体模型中，流道进口断面的几何中心为三维坐标系的原点，Gx为x 轴正方向，表示流道内水流方向。4 种形式流道单元平面尺寸及三维建模见图1。

利用Fluent 软件对上述已结构建模的4 种形式迷宫流道内部进行水流速度场模拟分析，根据模拟出的各流道内流线及涡漩分布情况，利用画图工具尽可能地将流道内的涡漩区域去除，借助Gambit 软件进行无漩涡流道的建模，得出4 种尺寸相对应的无涡流道几何模型。尺寸参数见表2。

4种形式的无涡流道单元平面尺寸图及三维建模见图2。

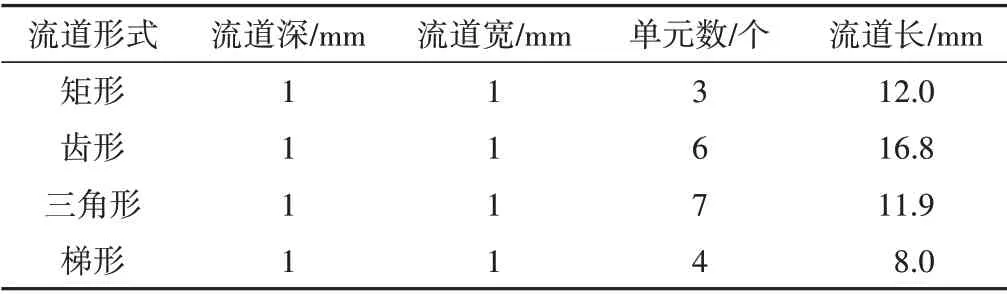
表1 有涡迷宫灌水器尺寸参数Tab.1 Dimension parameters of labyrinth emitter with vortex

表2 无涡迷宫灌水器尺寸参数Tab.2 Dimension parameters of labyrinth emitter without vortex

1.2 边界层的选取及网格划分

在利用Gambit 建模软件1∶1 建模时，各迷宫灌水器模型的速度入口断面和自由出流断面上均设置边界层，其中第1层边界层的厚度为0.01 mm，边界层数为6，总厚度均为0.208 mm，计算网格划分方法选用Hex/stairstep 网格，其网格间距为0.05 mm。划分后的矩形有涡流道网格数239 360 个，网格节点262 568 个；矩形无涡流道网格数104 282 个，网格节点121 862个。齿形有涡流道网格数96 898个，网格节点110 588个；齿形无涡流道网格数40 080 个，网格节点49 844 个。三角形有涡流道网格数121 088 个，网格节点139 725 个；三角形无涡流道网格数61 490 个，网格节点74 451 个。梯形有涡流道网格数40 960 个，网格节点48 161 个；梯形无涡流道网格数13 568个，网格节点18 462个。其中以梯形有涡流道4个单元网格划分及梯形无涡流道4 个单元网格划分结果为例，见图3。

2 计算模拟结果及分析

2.1 有涡和无涡流道灌水器的流场分析

以矩形、齿形、三角形、梯形4种流道灌水器模型为研究对象，通过Fluent 软件对4 种流道迷宫灌水器进行流场的模拟，并利用Tecplot 后处理软件对该4 种模型进行速度流场的分析，可以清楚地了解4种流道灌水器内部水流的流场运动情况。在各个流道灌水器的z=0平面进行速度场的模拟，并绘制速度矢量图，见图4。

如图4所示，迷宫流道内的水流流动主要包括位于流道边壁处、夹角处的堵塞区与水流运动正方向的主流区。主流区内的水流流速较大，流线沿流道分布均匀，且不易受流道转角的影响，流道内的沙粒不易在此区域内沉积。堵塞区内的水流流速较小，流线易受流道转角的影响脱离主流而形成封闭的漩涡，流道内的微小颗粒会在此区域内沉积而造成灌水器的堵塞。因此，利用计算流体力学（CFD）数值模拟可视化地揭示了4种形式流道内部流场运动情况及水流流动的速度矢量图，进一步借助AutoCAD 画图软件和Tecplot 软件的处理分析，对矩形、齿形、三角形、梯形4种有涡流道灌水器模型基进行结构优化，最大限度地消除了堵塞区内漩涡对流道水力性能的影响，并从结构上解决流道堵塞的问题，建立了4种形式相对应的无涡迷宫流道模型。并对4种无涡迷宫流道内水流运动情况（速度场）进行数值模拟和分析，绘制出各个无涡流道灌水器流道在z=0平面上的速度矢量图，见图5。

由图5可知，4 种形式无涡流道内最大限度的消除了涡漩对水流的影响，流道内水流流线均沿着主流区流动，抗堵性能良好。同时，4种形式无涡流道以消除流道内的旋涡区即堵塞区为目标，按照流道内主流区速度流线的外边缘为流道的边界，确定出流道的结构形状为圆弧形，具体尺寸见表2及图3。通过确定出的4 种形式无涡流道，利用计算流体力学（CFD）数值模拟软件对无涡流道内水流的水力性能做进一步研究与分析。

2.2 压力速度关系

利用Fluent 软件进行数值模拟，在3、5、7、9、10、12、14、15 m 的压力水头条件下，假定速度入口值，经模拟后读出该速度值下的速度入口断面面加权平均压强与自由出流断面面加权平均压强以及2者之间的压强差。此压强差需乘以实际迷宫流道单元数与模拟流道单元数的倍数，最终得出灌水器的实际压强差，从而得出灌水器的水头损失。此结果若与假设的压力水头值不符，则再假设速度入口值，直到模拟结果所得出的压力水头与给定值接近为止。速度流量计算公式为：

式中：q为灌水器流量；v为断面平均流速；A为灌水器流道断面面积。

在给定的不同压力水头条件下，不同形式迷宫流道内的水流速度值见表3。根据表3的数据可得出各个模型迷宫流道灌水器内水头损失与断面平均流速关系曲线，见图6。

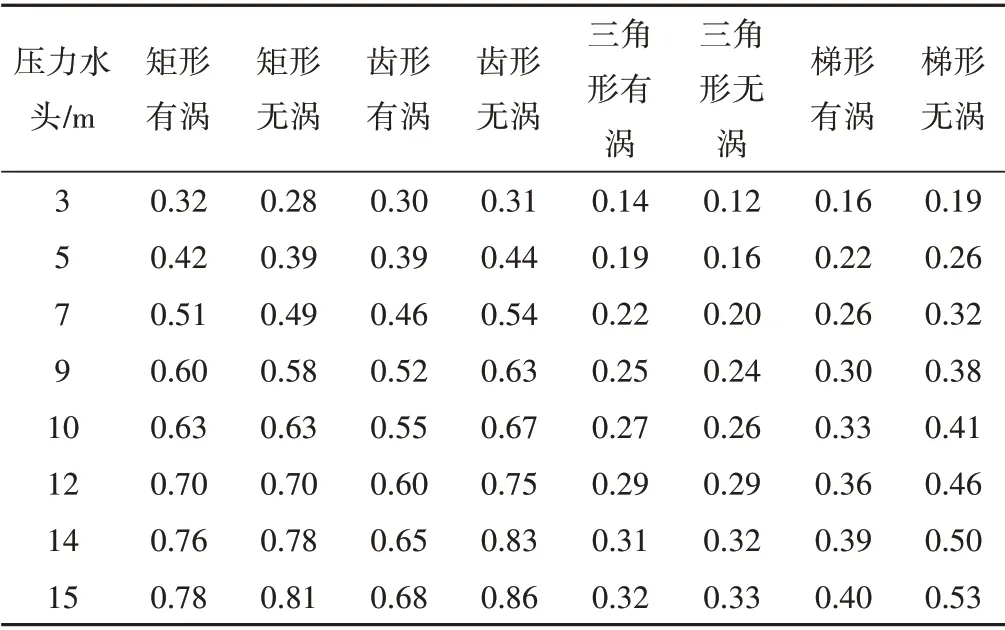
表3 不同压力下迷宫流道灌水器内水流速度值 m/sTab.3 Flow velocity in labyrinth channel emitters with different pressure heads

根据图6可知：①有涡迷宫流道中水头损失与流速的线性斜率为1.75～2.00，说明此时流道内水流流态为湍流。②无涡迷宫流道中水头损失与流速的线性斜率为1.49～1.60，说明无涡迷宫流道内水流流态更接近层流流态，湍动程度较有涡迷宫流道不明显。

2.3 压力流量关系及流量系数和流态指数的分析

通过Fluent软件数值模拟，可以得出不同形式的迷宫流道在给定压力水头下的流量值，其结果见表4。根据表4内数据得出4种形式有涡迷宫流道灌水器及无涡迷宫流道灌水器的压力与流量关系，见表5。由表5可知：①4 组有涡流道迷宫灌水器的流态指数均靠近0.5，说明有涡流道迷宫灌水器压力补偿性较低，压力的变化对迷宫流道内水流流量的影响较小，抗堵性能及水力性能较好。②同种形式的有涡流道迷宫灌水器与无涡流道迷宫灌水器相比，流道内水流的流态指数较小、流量系数较大。说明在去掉涡旋后的迷宫流道灌水器内，无涡迷宫流道灌水器的压力补偿性增大，流道内流量对压力的敏感程度增大，灌水器的水力性能变差。

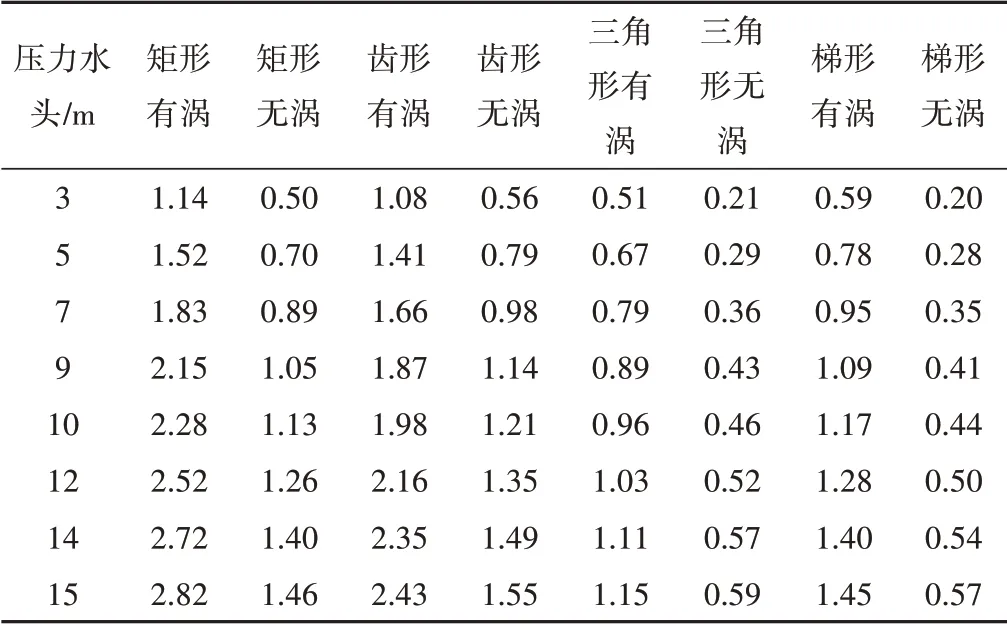
表4 不同压力水头条件下各形式迷宫流道灌水器内流量值 L/hTab.4 Flow rate in labyrinth channel emitters with different pressure heads

表5 各形式迷宫流道灌水器内压力与流量关系Tab.5 Relationship between pressure and flow rate in labyrinth channel emitters

3 结 论

（1）迷宫流道灌水器内的水流流动可分为沿着流道运动的主流区和堵塞区，堵塞区内由于涡漩的存在使流道内微小颗粒在此区域内沉积而引起流道的堵塞。借助CFD 模拟软件、AutoCAD 画图软件及Tecplot 后处理软件，最大限度地按照流道内主流区速度流线的外边缘为流道的边界设定不同形式的无涡流道模型，从结构上解决了涡漩对于不同形式流道的影响，极大提高了流道内的抗堵性能，为迷宫流道灌水器的结构优化设计提供了一定理论基础。

（2）无涡流道进口处流线相互平行且稳定，水流流态为层流。整个无涡流道中由于没有涡漩的存在，无涡迷宫流道内水流流态介于层流与湍流之间的过渡区，流道内水流流线湍动不明显，流道中水头损失与流速的1.49～1.60 次方成比例；有涡迷宫流道中流道内水流流态为湍流，流道中水头损失与流速的1.75～2.00次方成比例，此结果与雷诺实验结果相符，流道内流线湍动明显。

（3）对于同一种形式的流道模型，流道去掉涡漩后，其流量系数均变小，流态指数均变大，说明此时流道迷宫灌水器的压力补偿性增大，流道内流量对压力的敏感程度增大，灌水器的水力性能变差。

（4）4 组模型的有涡流道迷宫灌水器的流态指数均靠近0.5，说明有涡流道迷宫灌水器压力补偿性较低，压力的变化对迷宫流道内水流流量的影响较小，抗堵性能及水力性能较好。

（5）涡漩的存在既可以造成流道内微小颗粒的堵塞，也可以增强流道内水流的湍动强度，有利于增强迷宫流道灌水器的水力性能。