相关向量机预测电池健康状态和剩余有效寿命

张之琦，郁亚娟，李 茜，胡宇辰，黄 凯

(1.北京理工大学材料学院，北京100081；2.北京林业大学环境科学与工程学院，北京100083)

通常当锂离子电池的容量下降至其标称容量的某个特定阈值之后就很可能会出现电池故障，对锂离子电池剩余有效寿命进行预测有着重要意义。在电池剩余寿命的预测中，健康状态(state of health，SOH)和剩余有效寿命(remaining useful life，RUL)是两个重要的研究指标[1]。RUL 指的是在器件的生命周期中无法实现其基本功能的时间，通常定义为从当前时间到系统或者组件出现故障的时间。SOH 描述的是老化电池与新电池相比的物理健康状况[2-6]。

目前针对锂电池容量的研究方法主要分为两种，一种是基于模型预测电池容量，一种是通过数据驱动实现预测[7]，如图1 所示。但是基于模型进行预测的问题在于这类模型对电池的老化过程很难建立复杂的数学模型来进行准确的模拟，所以在数据量充足的时候常常使用数据驱动的方法来进行电池容量的预测，这一类方法忽略了一定的电化学特性，仅基于电化学数据中提取出的特征来预测电池容量[8]。

近年来智能技术的发展，特别是机器学习研究的热潮极大地推动了数据驱动的RUL 预测技术的发展，例如各种神经网 络[9]、随 机 森 林[10]、支 持 向 量 机(support vector machine，SVM)[11]和用于电池RUL 预测的相关向量机(relevance vector machine，RVM)[12]。然而很多机器学习算法在应用中都有着局限性：决策树得到的最终结果很可能收敛于局部最优解；随机森林改善了决策树的一些不足，有着优于SVM 的训练速度，但是偏倚增大，在解决回归问题时表现欠佳；多层感知机的神经网络消耗很多计算资源，同时在对参数进行优化后很容易导致过拟合；隐式马尔科夫模型需要大量的数据训练才能得到精确的模型；深度学习模型虽然有着更高的精度和鲁棒性，但是模型复杂度更高，训练时间更长，面对小样本场景时表现不佳，在很多情况下并不适用；SVM 模型有着不错的精确度以及抵抗噪声的能力，在大规模的数据中也有着不错的表现，但是SVM 模型中的参数需要经过交叉验证，SVM 的核函数需要满足Mercer 定理并且结果无法以概率的形式输出[13]。研究者们一直致力于开发新的思路，SVM 是剩余寿命预测中研究最为广泛的机器学习算法之一，与其有着相同广义数学模型的RVM 因此受到了研究者的关注。

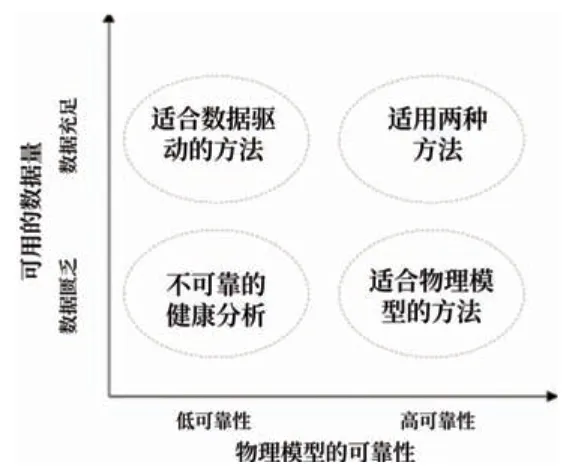
图1 基于模型和基于数据的算法对比[8]

RVM 作为一种机器学习技术主要用来解决回归和分类问题。RVM 虽然是一种和SVM 具有相同广义数学模型的算法，但是它避开了SVM 算法的很多不足，解决问题的思路也和SVM 算法截然不同。RVM 是一种基于贝叶斯的稀疏核算法，与SVM 法最大的区别是提供了对输出数据的概率解释[14]。除此之外，RVM 避开了SVM 的很多先天缺陷，例如SVM 算法中所使用的核函数对应的核矩阵需要满足Mercer条件，这使核函数的选择变得苛刻，同时SVM 对于算法中的超参数需要进行交叉验证，而这个过程非常消耗计算资源，严重影响模型的效率[15]。RVM 在回归问题上还有着优良的控制“欠拟合”和“过度拟合”的能力[16]。这些优势使得RVM在预测剩余有效寿命研究中受到关注，并且在理论和实验上都证明了RVM 在训练回归模型的时候有着不错的泛化性能[17]。

但是RVM 算法同样存在一些先天缺陷，例如在训练RVM 模型时使用的一些核函数有可能会使最终的输出结果收敛于一个局部最优解而不是全局最优解，同时RVM 算法训练的过程中需要进行矩阵之间的相乘和矩阵求逆的操作，这使得一些RVM 算法的时间复杂度达到了O(M3)，空间复杂度来到了O(M2)，其中M 表示首次需要进行训练的样本数量，这意味着RVM 模型在面对大样本对象的时候表现不佳[18]。已有很多研究表明RVM 算法在长期预测应用中表现不理想，导致模型对于锂离子电池RUL 的长期预测结果和实际偏差较大。基于单一RVM 算法的预测模型在在线实时预测系统中对锂离子电池的RUL 判断同样表现堪忧。为了解决这些问题，近年来很多研究针对RVM 算法提出了解决方案，希望优化RVM 模型在RUL 预测中的表现[19]。

本文对近5 年来关于RVM 的出版材料进行了系统研究，以期提供RVM 算法在电池剩余寿命预测中的主要发展趋势和潜在应用。

1 RVM 算法介绍

RVM 和SVM 有着相同的广义数学模型：

式中：y(xi;ω)为一个未知的非线性数学模型；ε 为RVM 模型中常用的一个满足高斯分布的噪声，其均值为0 且方差为σ2。

模型中的非线性数学公式y(xi;ω)表示为：

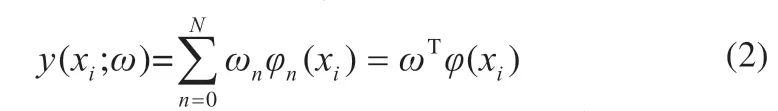
式中：φ(xi)=[1, k(xi, x1),(xi, x2),…,k(xi, xN)]T；φ(xi)为每个训练样本经过核函数扩展之后的基函数；ωn为每个样本所带有的权重；ω={ω1,ω2,…,ωN}为一个包含权值的向量。

式(2)可以简写为：

式中：Φ 为一个N×N+1 的设计矩阵。

整合式(3)得到：

假设模型的残差符合高斯分布，同时为了书写简便令β-1=σ2，之后得到：

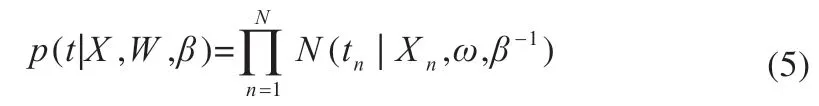
通过最大化式(5)，求偏导即可求得ω 和β-1，但是如此求得的模型很容易出现过拟合的缺陷，所以需要先给ω 定义一个先验分布来解决过拟合的问题[20]。 ω 先验分布可以表达为：

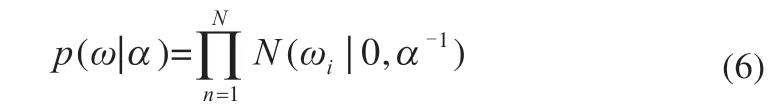
参数ω 的后验分布可以表示为：

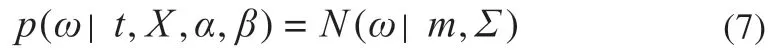
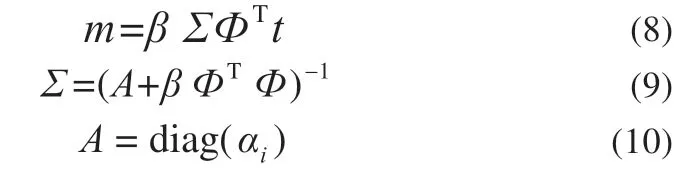
结合贝叶斯统计学中的边缘似然函数(marginal likelihood function)就能写出目标的概率分布：

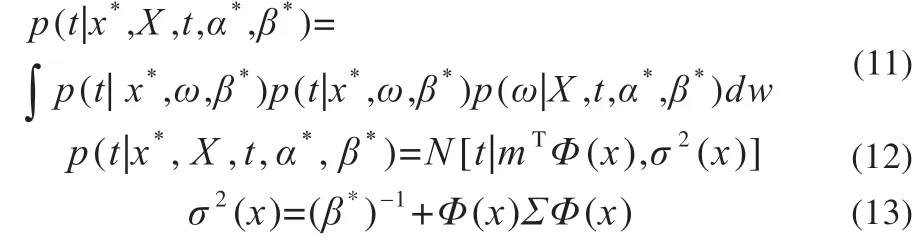
式(12)中mTΦ(x)表示高斯分布的均值，σ2(x)表示高斯分布的均方差，之后求得N[t|mTΦ(x),σ2(x)]的极大值就能得到其中的超参数α*和用来表示噪声方差的β*。如此就能得到概率分布模型的表达式。目前RVM 的最大期望(expectation maximization，EM)迭代方法也得到了广泛的应用，其原理如图2 所示[18]。

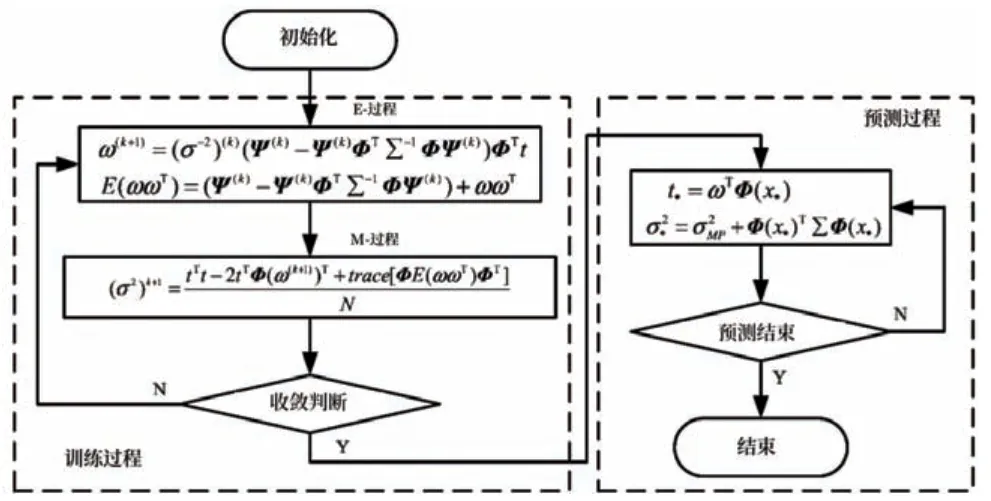
图2 RVM的EM迭代流程

2 RVM 在RUL 中的应用

本文中将RVM 预测的优化分为以下四个部分。

2.1 核函数的优化

为了提升RVM 在RUL 预测中的表现，很多研究尝试在RVM 模型中使用多个核函数优化模型，但引入多个核函数必然导致需要拟合的参数增加，无疑会增大训练的时间和复杂程度。针对RVM 核函数的研究重心是希望解决单核RVM 算法中存在的缺陷，利用优化方法寻求最佳核函数的组成以获得更为准确的预测结果。优化核函数的简化方案如图3 所示。

王春雷等[21]将核函数进行组合来优化模型，使用高斯核函数和多项式核函数构成的组合核函数代替原有的单一核函数来提高模型的泛化性能。研究结果表明，使用组合核函数的RVM 模型和使用单一核函数的方法相比，虽然效率略有降低但是准确性得到了提高。通过人工试值来调整核函数的关系仍旧具有很大的主观性而且不全面，Yang 等[22]使用离散粒子群优化(discrete particle swarm optimization，DPSO)的策略来计算RVM 核函数最优组合，结果表明自选择核函数的RVM 模型的训练结果优于之前的RVM 模型。

图3 使用RVM 进行预测的简化流程

类似的，在Zhang 等[23]的研究中使用粒子群优化(particle swarm optimization, PSO)法实现了对核函数的组合优化。Chen 等[24]通过杜鹃算法智能地实现对RVM 中每个核函数的参数确定以得到对RUL 问题求解的最佳组合。与RVM 核杜鹃算法相结合的CS-HKRVM 算法使用混合核的策略，由于泛化能力和学习能力的提升，在数据测试中已经被证明优于单核RVM 模型。在刘月峰等[25]的研究中，果蝇优化算法(fruit fly optimization algorithm，FOA)被用来寻找组合核函数之间的组合方程系数。值得注意的是该研究为了减少模型中需要同时拟合的参数数量，首先训练单核RVM 来确定较好的超参数，在保持超参数不变的基础上组合多个核函数。结果表明基于FOA 群智能优化的RVM 有着比单核RVM 模型更好的预测精度。

2.2 结合物理模型的RVM 融合算法

数据模型混合方法不仅可以反映电池的退化机理，而且可以从数据集中获得电池健康状态的信息和演化规律，一定程度上解决了数据模型忽略物理特征和物理模型过于复杂的缺点[26]。

Wang 等[6]设计了基于RVM 和三参数容量退化模型相结合的预测方法，来进行对锂离子电池剩余寿命的预测，实验结果很好地表征了周期和容量之间的下降趋势。

卡尔曼滤波器(Kalman filter，KF)是一种数据融合的算法，该算法中只需获得上一刻的系统的估计值和现在的观测值就能得到现在系统状态的估计值，所以不需要记录观测或者估计的历史信息。在很多研究中卡尔曼滤波器用来实现物理模型与RVM 方法的结合，其中RVM 的预测分布作为卡尔曼滤波器中的观测值，与模型的预测分布进行结合，实现数据驱动方法和物理模型方法的融合。其基本流程如图4 所示，虽然已经得到应用的卡尔曼滤波器种类很多，但基本原理类似。

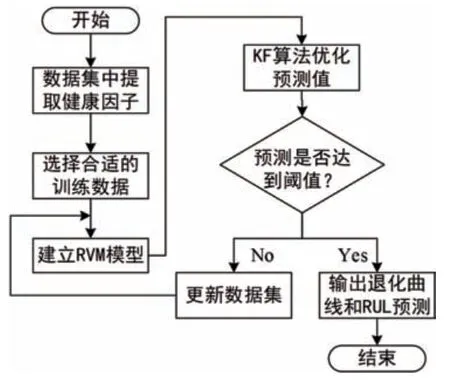
图4 RVM结合卡尔曼滤波器建立融合模型的简化流程

Yuchen 等[19]结合了RVM 算法和卡尔曼滤波器算法，实现了将锂离子电池RUL 的长期预测变成一些较为精确的短期预测。利用RVM 算法进行精确的短期预测后，利用卡尔曼滤波器将每一次的RVM 短期预测结果优化后用于更新数据集，进行重新训练得到新的相关向量和系数矩阵，更新后能够得到较为稳定的对下一个周期的容量的预测结果。在Zheng等[27]的研究中提出了一个类似的结合算法，不同的是该研究针对RVM 迭代计算中的累积误差，采用加权函数来调整误差对于预测结果的干扰，并根据预测过程的变化，开发了一种自适应协方差更新方案。

刘贵行等[28]利用差分进化算法和粒子群优化算法来优化RVM 中的参数，最后利用KF 结合物理模型对RVM 模型的预测结果进行降噪以此来削弱噪声的影响，同时将优化后的预测结果作为在线样本添加到训练集中，对提出的模型重新训练，以此来动态调整系数矩阵和相关向量以执行下一次迭代预测。

除了经典的KF 模型以外，一种用于非线性系统的无迹卡尔曼滤波器(unscented Kalman filter，UKF)也被用来和RVM 模型进行结合。其中的RVR 模型为UKF 提供残差的未来演变，利用UKF 来实现预测过程中对电池模型参数的连续更新。经过实验验证，得到了优于单一RVR 和UKF 模型的结果[8]。

除卡尔曼滤波器之外，粒子滤波器(Particle filter，PF)也被用来建立融合模型。粒子滤波器是一种使用重采样算法和一组加权粒子来近似概率密度函数(probability density function，PDF)的计算模型[29]。在这类模型中RVM 常被用来从先前的电池退化数据，查找代表性的训练向量，然后通过拟合提取的训练向量来识别开发的容量损失模型。图5 是这类预测模型的基本流程图，虽然各项研究之间有所差异，但基本思路一致。

图5 结合RVM进行预测的简化流程

2007 年RVM 首次被用来预测电池寿命所采用的方法就是与PF 模型进行结合，在之后的一年Saha 等人的研究中再次提出了将RVM 和PF 结合的模型。研究中使用了Rao-Blackwellized PF(RBPF)框架来减少预测结果的不确定性。简单的将PF 和RVM 模型结合会因为RVM 模型使用EIS 数据的离线性，导致模型不能通过在线数据更新模型参数[30]。

使用RVM 和PF 模型并且同时利用Monte Carlo(MC)模拟和Kullback - Leibler(KL) 发散的verification and validation(V&V)方法来校准PF 的粒子数和模型噪声，来提高模型预测的准确性，并实现通过在线数据更新模型的参数，得到了不错的模拟结果[31]。

2.3 健康指标的优化

利用RVM 实现对电池剩余有效寿命的预测，这种基于数据的预测方法与监测的数据有很大的关系，模型要求有大量的实验数据才能实现稳定的建模，选择合适的健康指标能够提高模型的精确度以及减少训练的消耗。

Zhou 等[7]从锂离子电池的工作参数中提取了一种新的健康指标(HI)。研究中使用的HI 由电池的放电电压形成，这些电压的数据易于通过在线方式获取，解决了之前训练数据离线性的问题。经过处理的HI 数据利用RVM 模型实现对电池RUL 的预测。得到的结果表明优化的RVM 在RUL 预测中会得到更为准确的结果。

为了减少初始训练数据中的噪音造成的影响，Zhang 等[23]使用经验模态分解方法(empirical mode decomposition, EMD)和多核相关向量机(multi-kernel RVM，MKRVM)结合的电池容量预测方法。EMD 去噪方法用于处理测得的容量数据，以产生无噪声的容量数据。基于去噪后的容量数据，构建了使用MKRVM 的电池容量预测模型。

Zhang 等[32]从电池充电和放电过程的充电电压、电流和温度曲线中提取特征来表征电池的老化过程，通过这些健康特征(health feature,HF)建立的模型取得了不错的结果。于是有研究通过灰色有理分析从充电电压、电流和温度曲线中的14 个HF 中提取出和电池老化相关的5 个高相关性的HF。将这些经过处理的HF 数据作为RVM 模型的输入，验证了经过HF 萃取的特征作为健康指标有不错的预测结果[33]。

Widodo 等[17]使用样本熵处理放电电压的信息并将得到的数据作为建立模型的参数，利用样本熵功能和估算的SOH来评估电池的退化率，较为准确地实现了对于电池退化状态的描述，同时反映电池的健康状态。

传统的检测方法都是基于一些集总的性能指标，类似于容量、电阻和电压等，而这些指标都是很多物理参数的复杂函数。虽然基于这些集总参数的方法很容易实现，但是精确度有限。所以开发基于物理化学参数的诊断方法在一些情况下变得很有意义，Zhou 等[34]通过将EIS 与机器学习方法相结合，实现了RVM 无模型物理级电池诊断方法，向物理级电池诊断迈进了一步。为了解决传统性能指标预测不准确的问题，Zhang 等[35]选择了5 个间接指标作为训练模型的健康指标，使用归一化的方法解决多参数的维度问题，同时在模型中使用动态参数，结合粒子群优化得到最终的模型，经过验证得到了令人满意的结果。

2.4 其他优化方法

Zhao 等[36]使用了RVM 和灰色预测模型(gray forecast model，GM)来预测电池的健康状态，根据预测结果更新训练数据集，然后更新RVM 和GM。RVM 和GM 不断地相互校正彼此的预测结果，结果表明这个过程减少了预测的累积误差并提高了电池SOH 的预测精度。Liu 等[18]在RVM 模型上应用增量学习的策略，提出了增量优化相关向量机(incremental optimized RVM，IP-RVM)算法。该方法相比于离线的RVM，提高了预测的准确性，与再训练RVM 预测的精度接近但是时间消耗明显减少。在此之后，范兴明等[37]利用增量学习的策略建立了实时处理数据的RVM 模型。

3 总结

RVM 算法作为机器学习中一个用于分类和回归问题的算法，在电池寿命的预测中受到了越来越多的关注，但是RVM 模型在应用的时候仍然面临着很多有待解决的问题。建议RVM 在未来电池寿命预测中的重点研究方向为：

(1)重点关注RVM 算法和其他算法的结合，特别是与基于模型预测电池寿命的方法相结合，充分利用RVM 在寿命预测中泛化性能好以及模型稀疏的优点，并通过结合其他算法解决RVM 在长期预测中的问题。

(2)追踪RUL 预测中对于新健康指标的研究，并将这些指标应用于RVM 模型，解决目前常用指标离线性的缺陷。

(3)注重实际使用中不确定性问题的处理，改进RVM 算法提高预测的精度。