基于GSASO的局部阴影下光伏最大功率追踪

卢文韬， 肖 辉， 吴姿瑾， 王至远

(长沙理工大学电气与信息工程学院，湖南长沙410114)

太阳能在能源比例中日益增长，但目前光伏利用率很低，而最大功率点追踪(maximum power point tracking，MPPT)技术是提高光伏利用率的关键技术之一。传统的MPPT 算法，如电导增量法、扰动观测法等，在光伏阵列处于均匀光强条件下追踪，表现出可靠性高、结构简单等优点[1]。

在实际运行中光伏阵列可能受云层、树木和建筑物的遮蔽，从而使光伏阵列运行在局部阴影条件(partial shading condition，PSC)下。在此条件下，光伏系统的P-V 特性曲线具有多个局部最大功率点(local maximum power point，LMPP)[2]。上述传统MPPT 算法由于无法区分全局最大功率点(global maximum power point，GMPP)和LMPP，在寻优过程中易陷入局部最大功率点，而导致发电效率较低的问题。

为解决在局部阴影下传统方法容易失效的问题，许多学者致力于研究基于群体智能优化算法的MPPT 技术。文献[3-9]把粒子群、人工蜂群等智能优化算法和各种改进优化算法应用到光伏发电系统MPPT 控制中，来提高追踪速度与准确度，有效解决了传统MPPT 方法不能准确追踪全局MPP 而错误追踪到局部MPP 的问题，从而减少功率损失，但是存在收敛速度较慢等不足。文献[10]引入混沌序列方法与鸡群算法结合，避免算法陷入早熟，提升了追踪效率，但是没有设置动态光照条件下算法追踪的重启条件。

原子搜索优化算法(atom search optimization，ASO)是模拟动态分子行为的新型智能算法[11]，在寻优过程中表现出良好的收敛精度，但ASO 在寻优过程中的收敛速度较慢且易陷于局部最优解。黄金正弦算法(golden sine algorithm，Golden-SA)是Tanyildizi 等在2017 年提出的新型元启发式算法[12]，具有收敛精度高、收敛速度快等优点。将ASO 与Golden-SA 融合构造成黄金正弦混合原子搜索优化算法(atom search optimization based on golden-sine algorithm，GSASO)[13]。将其应用于光伏系统MPPT 控制中，来提高追踪速度与准确度，最后用Matlab/Simulink 搭建模型来仿真验证。仿真结果表明，相比于PSO 和ASO 算法，基于GSASO 的MPPT 收敛速度快，并减小了陷入局部MPPT 追踪的可能性，提升了追踪性能。

图1 所示为光伏电池的等效模型。图中：Iph为太阳电池的短路电流；Id为暗电流；I 为太阳电池的输出电流；Rsh为并联电阻；Rs为串联电阻。当光照恒定时，光生电流Iph不随光伏电池的工作状态而变化。

1 光伏发电系统

1.1 光伏电池数学模型

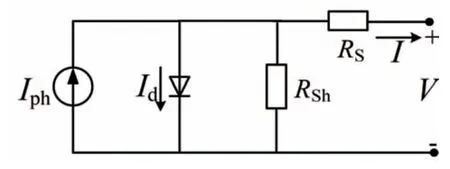
图1 光伏电池等效模型

假设等效二极管D 的端电压为Ud，则光伏电池输出电流表达式为：

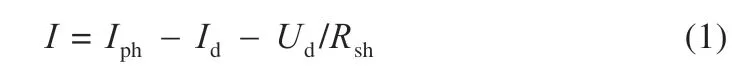
暗电流为：

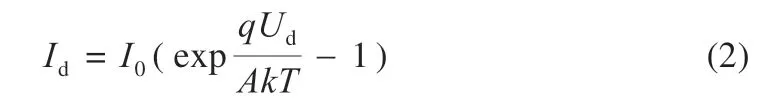
由式(1)、(2)可得：

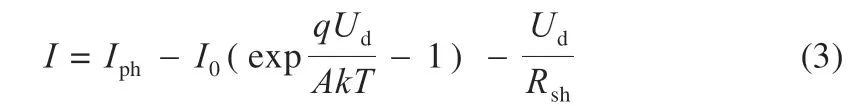
式中：I0为反向饱和电流；q=1.6×10-19C 为电子电量；K=0.86×10-4eV/K 为玻尔兹曼常量；T 为绝对温度；A 为PN 结理想因子。

1.2 局部阴影下的光伏输出特性曲线

光伏系统在局部阴影环境下，P-V 输出特性曲线是一条多峰曲线[14]。用Simulink 搭建4×2 的光伏阵列模型。设置环境温度25 ℃，辐照模式如表1 所示；光伏阵列的特性曲线如图2 所示。

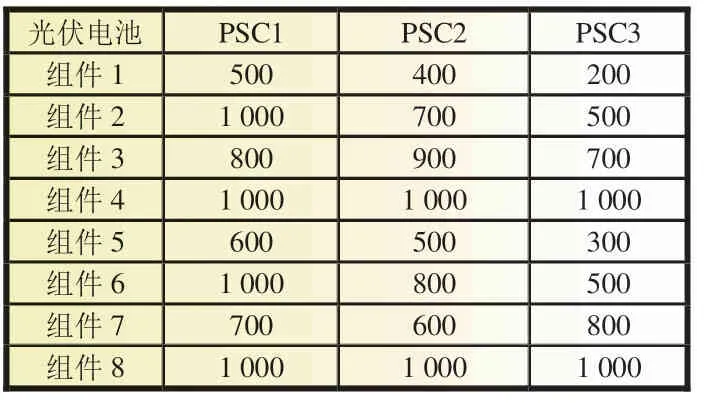
表1 局部阴影下的光照模式 W·m-2

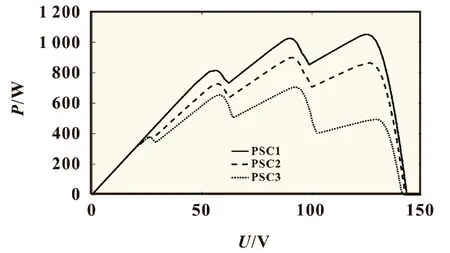
图2 光伏阵列的P-V特性曲线

2 基于GSASO 的MPPT 方法

2.1 原子搜索优化算法(ASO)

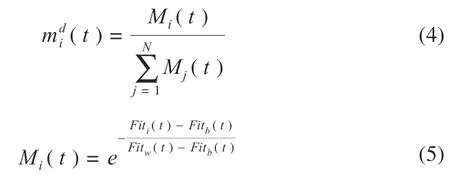
式中：Fit(t)为搜索过程中原子的适应度值，Fitb(t)为搜索过程中第t 次迭代的最优适应度值，Fitw(t)为搜索过程中第t 次迭代的最差适应度值。

K 为邻近原子的数量，有：

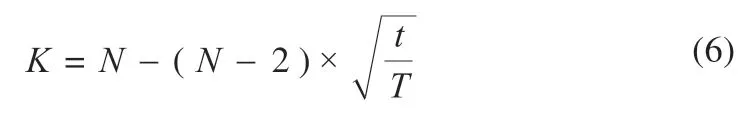
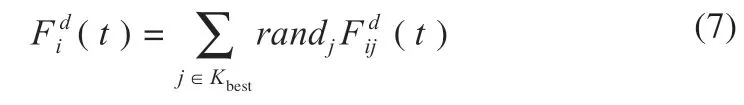
式中：Kbest表示在d 维空间搜索过程中适应度较好的邻近原子的集合(t )为搜索过程中两个原子之间的相互作用力。

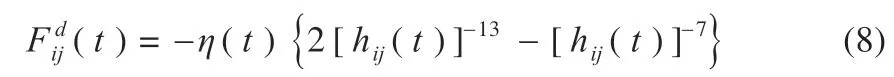
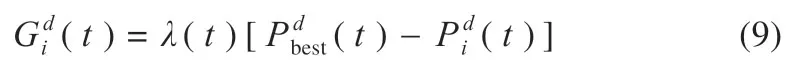
在d 维空间搜索过程中第i 个原子在第t 次迭代时的加速度表示为：

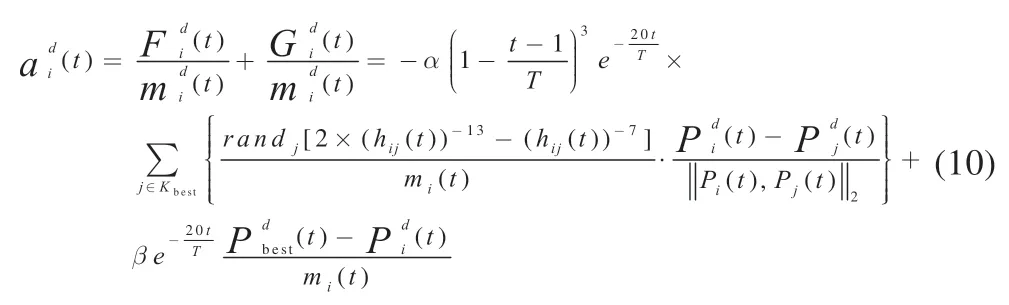
ASO 算法迭代的核心过程是通过加速度使原子速度发生变化，原子位置随着速度发生相应的变化，表示为：

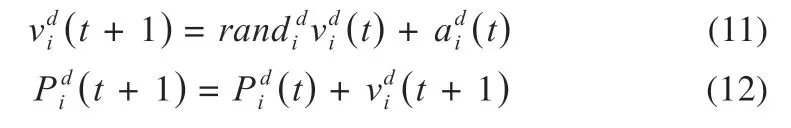
2.2 黄金正弦算法

黄金正弦算法通过黄金分割系数把解空间范围缩小到良性区域，能极大地提升收敛速度。

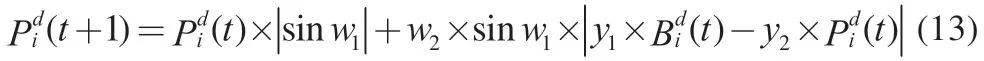
式中：w1和w2为随机数，w1∈[0,2π]，w2∈[0,π]；y1和y2为通过黄金分割法进行换算得到的系数，用表示黄金分割数。通过这些系数，能够把搜索空间锁定至良性区域，使原子个体一步步收敛至最优位置，从而提升算法收敛精度。

2.3 GSASO 算法在光伏MPPT中的应用

2.3.1 黄金正弦原子搜索优化算法

将Golden-SA 的核心过程作为局部优化算子与ASO 相结合，原子个体位置在每一次算法迭代的后期执行黄金正弦操作。这样可以与最优个体进行充分的信息交流，能够使原子个体跳出局部最优，极大地提升算法收敛速度。

将黄金正弦原子搜索优化算法(GSASO)应用到太阳能光伏电站最大功率追踪控制方法中，其中原子位置表示占空比D，则式(12)变为：

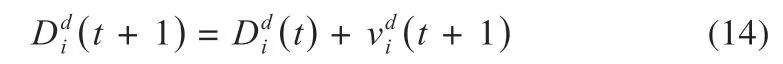
利用GSASO 的优势来提升收敛速度和减少陷入局部最优的可能性，从而实现最大功率跟踪，同时能提升MPPT 控制方法的追踪速度和精度。

本文所提GSASO 应用于MPPT 的具体步骤为：

(1)将GSASO 各参数和原子种群进行初始化；

(2)计算适应度值，并保存当前的最大功率值及最优占空比；

(3)原子个体(占空比D)的加速度、速度依次根据公式(10)、公式(11)来进行更新迭代；

(4)占空比D 根据公式(14)来进行更新迭代；

(5)对步骤(4)所生成的占空比执行黄金正弦操作，将其更新到新的位置(占空比)；

(6)再度计算适应度值，根据适应度值的大小来更新最优占空比和最大功率值；

(7)判断是否达到最大迭代次数或终止条件，如果达到就终止迭代，否则就重复步骤(3)～(6)；

(8)判断是否达到重启条件，如果达到重启条件就重复步骤(1)～(7)，否则就输出下一步；

(9)输出最优占空比以及最大功率值。

2.3.2 终止条件

为了能够在GSASO 迭代后期及时终止算法的迭代以减少输出功率波动，需要给GSASO 设置终止条件，MPPT 控制的输出为占空比，因此原子位置代表占空比，设置当原子间的最大位置差小于一个很小的阈值θ 时，认为已经追踪到最大功率点，终止迭代，θ 越小，精度越高。

2.3.3 重启条件

由于在光伏阵列实际运行中，其运行条件会不断发生改变，当这种改变足够大时就需要重启GSASO 算法，以搜索新的最大功率点[15]。采用的重启条件为：

式中：Pmpp为GSASO 算法搜索到的全局最大功率点功率；P 为光伏阵列的实时输出功率。

综上所述，基于GSASO 算法的MPPT 控制流程如图3 所示。

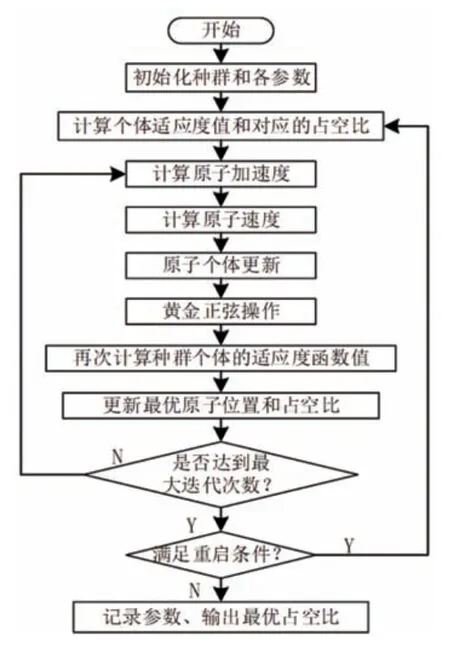
图3 基于GSASO的MPPT方法的流程图

3 仿真验证

为验证本文所提方法的可行性，用Simulink 搭建仿真模型，使用4×2 阵列的光伏系统来进行仿真实验。其中，将单个光伏电池的最大功率设置为213.15 W，将其开路电压设置为36.3 V，短路电流为7.84 A，最大功率点处的电压为29 V，电流为7.35 A。光伏MPPT 系统框图如图4 所示。

图4 基于Boost的MPPT系统

对MPPT 仿真模型中各电路元件进行以下参数设置[16]：C1=200 μF，C2=200 μF，L=0.15 mH。将Boost 电路的开关频率设置为50 kHz，基于GSASO 的光伏MPPT 算法的参数设置如下：粒子个数N=4，最大迭代次数为30，收敛条件θ =0.002，空间维度d=1，深度权重ɑ=50，乘数权重β=2，黄金系数y1=-π+(1-τ)×2π，黄金系数y2=-π+τ×2π。

3.1 局部阴影不变情况下的功率追踪

将光伏组件所受辐照度设为模式1。在此辐照条件下，光伏阵列最大功率为1 051 W，将其与PSO、ASO 算法追踪相比较，将仿真时间设为3 s。局部阴影不变情况下的仿真如图5 所示。

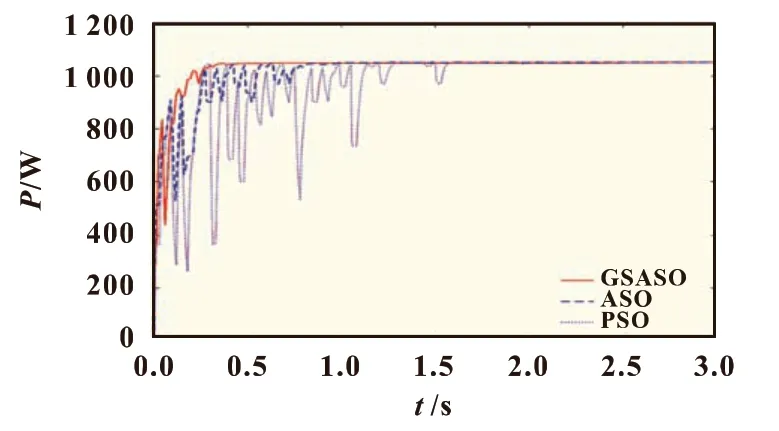
图5 光照强度模式1的输出功率仿真

由图5 可知，三种算法都能成功追踪到目标点，通过终止条件稳定到最大功率点；但是GSASO 方法的优化效率较高，收敛速度快，且追踪过程中幅值波动最小。GSASO 算法在0.3 s 时收敛到最大功率点为1 050.89 W，误差为0.010 4%；ASO 算法收敛速度较慢，追踪时幅值波动较大，在0.74 s 时才收敛到最大功率点1 050.85 W，误差为0.014 3%；而PSO 算法收敛速度最慢，追踪时幅值波动最大，在1.65 s 时才收敛到最大功率点1 050.57 W，误差为0.040 9%。

为进一步验证局部阴影不变情况下的功率追踪，将光伏组件所受辐照度设为模式2。在此辐照条件下，光伏阵列最大功率为899.6 W，将其与PSO、ASO 算法追踪相比较，将仿真时间设为3 s。仿真结果如图6 所示。

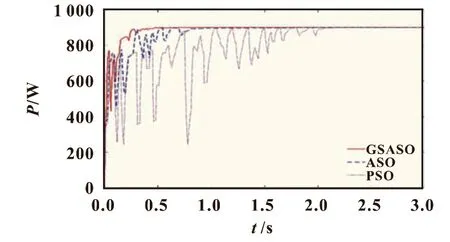
图6 光照强度模式2的输出功率仿真

由图6 可知，GSASO 算法在0.4 s 时收敛到最大功率点为899.48 W，误差为0.013 3%；ASO 算法收敛速度较慢，追踪时幅值波动较大，在0.8 s时收敛到最大功率点899.44 W，误差为0.017 7%；而PSO算法收敛速度最慢，追踪时幅值波动最大，在2.05 s 时才收敛到最大功率点899.29 W，误差为0.034 5%。通过在多种光照条件下的三种算法对比仿真，可以得出GSASO算法在MPPT 中的收敛速度和精度更高。

3.2 局部阴影突变情况下的功率追踪

当阴影情况发生变化时，对基于GSASO、ASO、PSO 的MPPT 算法进行下列参数设置，然后就其性能进行仿真实验。总仿真时间设置为6 s。在0 s 时，将光伏组件的辐照度设置为模式1，最大功率为1 051 W；在3 s 时，将光伏组件的辐照度设置为模式3，最大功率为704.8 W。仿真结果如图7 所示。

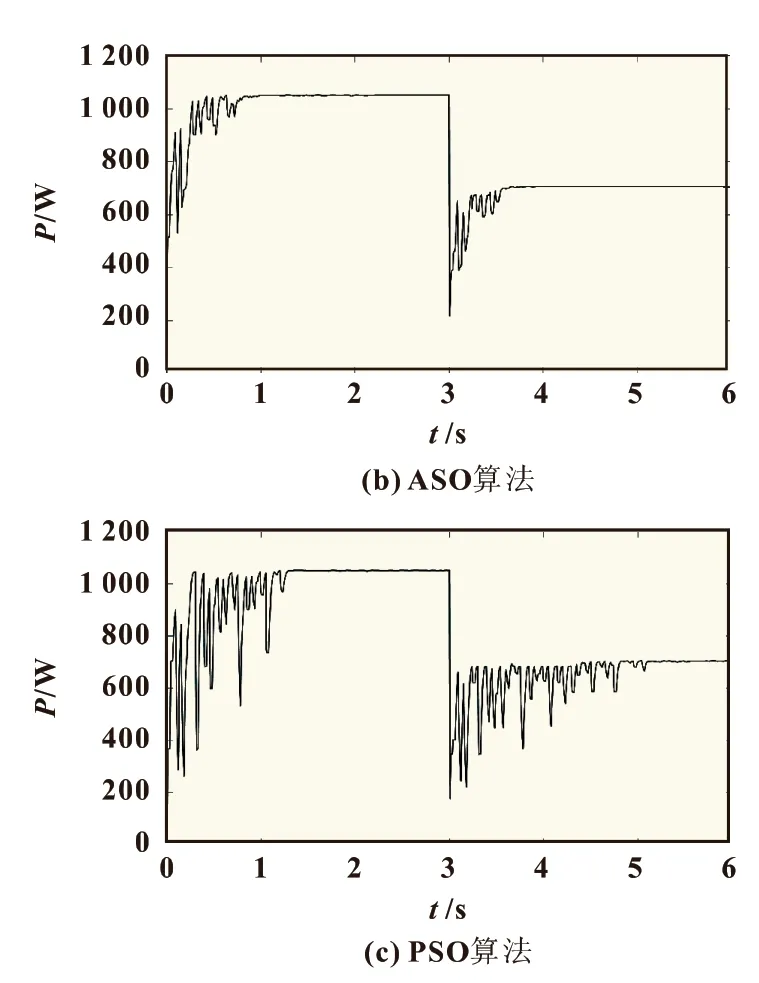
图7 局部阴影突变情况下的输出功率曲线

由图7 对比得知，三种算法均能在光照强度变化的情况下重新启动算法追踪到最大功率点，ASO 和PSO 在追踪过程中相较于GSASO 的收敛速度较慢，收敛精度较低。当辐照度为模式1 时，GSASO 在0.3 s 收敛到最大功率为1 050.89 W，误差为0.11 W；在3 s 时，辐照模式发生变化，辐照强度为模式2，GSASO 算法重启使光伏系统在3.3 s 时追踪到新的最大功率点为704.68 W,误差为0.12 W。GSASO 方法能够快速精确地在阴影突变环境下进行最大功率点跟踪。

4 结论

本文将Golden-SA 作为一种局部优化算子融入ASO 算法中，大大提升了算法的收敛速度和收敛精度。本文所提出的GSASO 与PSO 和ASO 在光伏MPPT 中通过仿真对比实验表明：

(1)在局部阴影不变的环境中，与PSO 和ASO 相比，GSASO 算法在MPPT 中的鲁棒性好，收敛时间极大地减少，从而提升光伏电池的利用效率。

(2)在阴影环境不断变化时，GSASO 算法也能通过重启算法，快速精确地追踪到最大功率点。

可知基于GSASO 算法的最大功率追踪方法，在局部阴影环境中表现出优良的性能，可提高光伏利用率。