锂电池SOC估算及改进型DC/DC变换器均衡电路研究
2021-04-02王伯瑞
王伯瑞, 郑 培
(内蒙古工业大学能源与动力工程学院,内蒙古呼和浩特010051)
锂离子电池组的不一致性会增加其过充(放)电的风险,并造成个别电池易老化,在工作中易老化的电池过充(放)电会加速其老化和容量衰减,降低电池组可用容量和寿命,当电池过充电量高于40%,温度上升显著,易引发热失控,增加电池组安全隐患[1-2]。因此,需引入均衡技术减轻不一致性,提高电池组能量利用率。
根据能量传递方式的差异,均衡电路分为被动均衡和主动均衡,主动均衡利用储能元件使能量在强弱电池间传递,已逐步取代低能量利用率、高散热量的被动均衡,成为研究热点,储能元件包括电容、变压器、电感等[3]。Cuk 斩波器通过电容使强电池放电和弱电池充电同步进行,纹波电流小,但均衡效果随能量传递路径的增长而下降,使更多无关电池参与均衡,且元器件多,成本偏高;变压器结构将各电池与副边连接,通过正反激原理实现能量转移,均衡速度快,但变压器铜损、铁损等会产生能耗,所需副边较多增加设计难度,拓展性差;双向DC/DC 变换器利用电感实现能量在相邻电池间传递,此结构适合短距离均衡,当能量差较大的两电池相距较远时,均衡速度减缓,且增加开关耗损[4-6]。
均衡策略的研究主要是选取均衡变量,荷电状态(SOC)与开路电压具有正相关关系,可以反映电压变化,且SOC 是综合量,可表征内阻和温度等参数,而端电压不能反映电池能量利用情况,在极限条件下电压波动大,不能反映电池内部参数,故SOC 为均衡变量较合理[7]。
SOC 估算方法包括Ah 积分法、Kalman 滤波法、神经网络法等,上述方法较成熟,但存在某些缺陷:Ah 积分法的SOC初值难以确定,且后期累积误差大;Kalman 滤波器对模型精度要求高,且高阶模型参数辨识繁琐;BP 神经网络易陷入局部最优,对初始权重敏感,且SOC 的影响因素多,使输入变量维数大,网络较复杂[8-10]。
综上所述,本文提出基于SOC 的双向DC/DC 变换器均衡方案。首先,设计开关阵列弥补DC/DC 变换器能量传递的局限性;然后,提出PCA-ACO-Elman 动态神经网络-UKF 联合估算算法,以SOC 极值和均值为均衡启停条件;最后,通过实验及Matlab/Simulink 仿真验证该方案的可靠性。
1 均衡电路分析
1.1 均衡电路结构
本文采用基于开关阵列的双向DC/DC 变换器电路,结构见图1。该电路由若干节锂离子电池、两组开关阵列和一个储能电感组成,其中锂电池为动力源,为汽车供电;开关阵列M 分为电池选择阵列和极性选择阵列,用于选择均衡充放电的电池序号及控制电流传递方向和大小,尽量选择阻抗较小的MOSFET 开关;储能电感L 作为能量传递媒介,用于吸收强电池的能量以向弱电池充电。

图1 均衡电路
1.2 均衡电路原理
当均衡功能开启时,以能量在B1、B2(强电池)和B6(弱电池)间传递为例进行分析,设PWM 输出占空比为D,均衡电路工作于电流断续(DCM)模式,故D<0.5,均衡周期为T,等效电路、回路电流大小和流向及PWM 对相关开关输出脉冲情况见图2。


图2 均衡示意图
阶段Ⅰ(0~t1):此阶段为强电池放电阶段。当处于0 时刻,PWM 控制M(1,1)、M(2,1)、M(2,8)、M(1,6)导通,导通时长为DT,B1和B2向L 释放能量,此时回路①的零状态响应方程为:
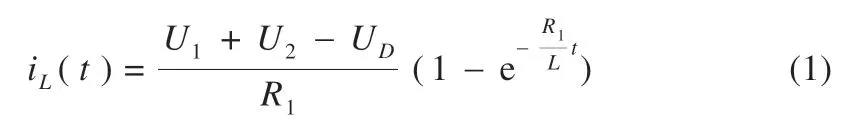
式中:UD为M3的导通压降;R1为放电回路损耗,包括上述4 个开关的阻抗、电感电阻等。
至t1时刻,回路电流达到峰值imax。

此阶段L 储存的能量为:

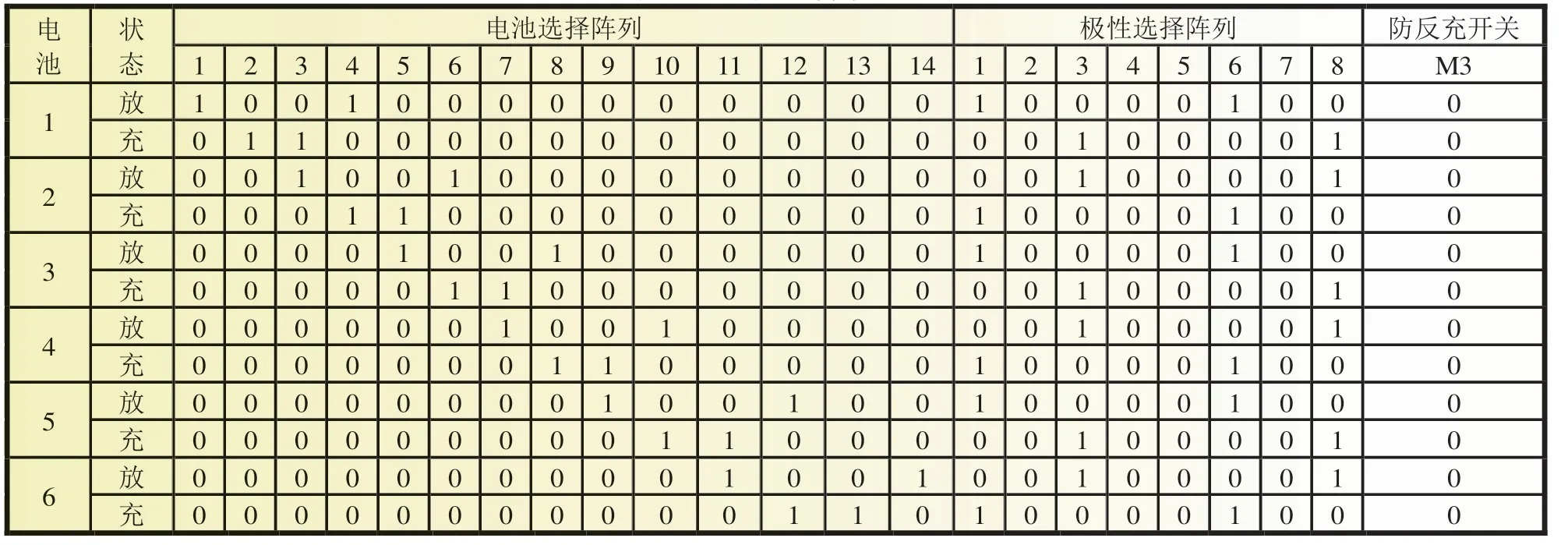
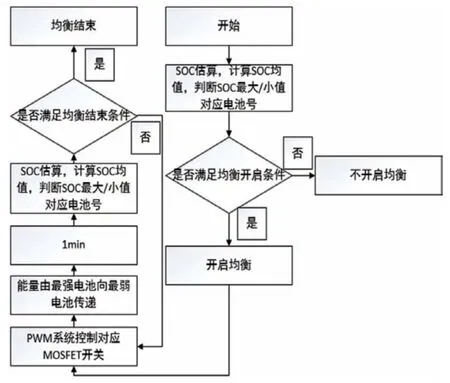
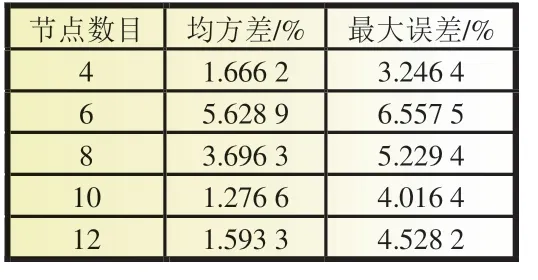
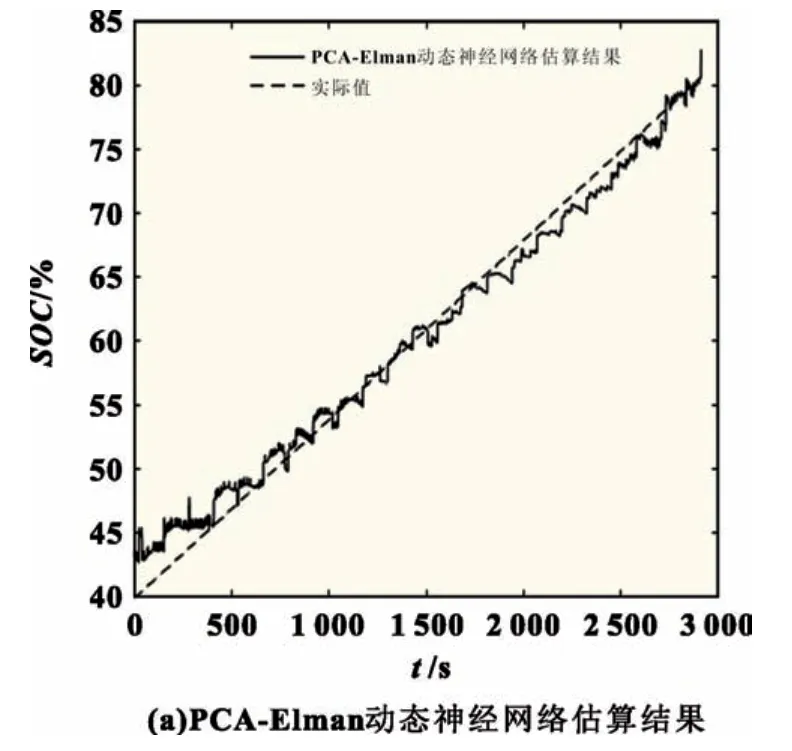
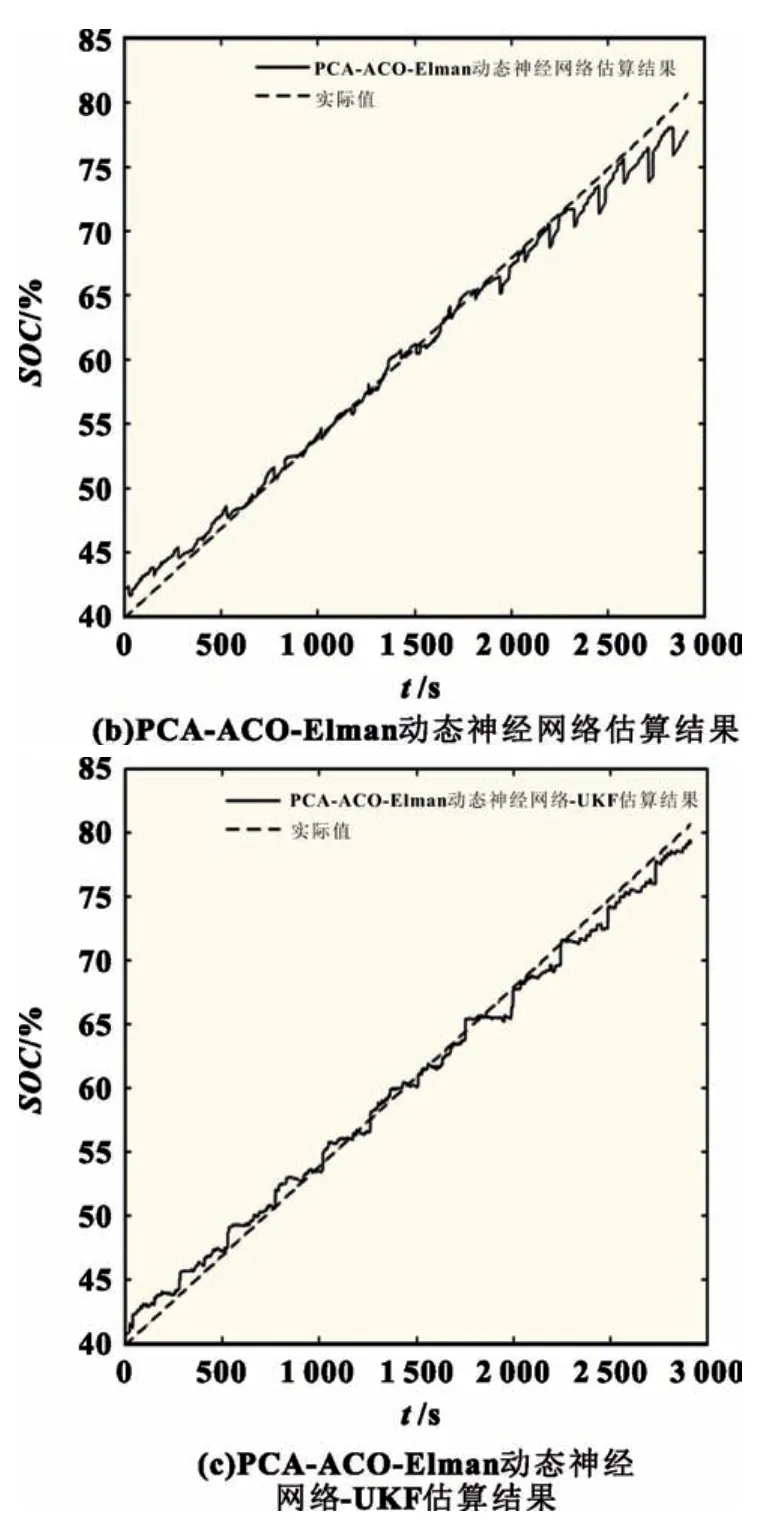
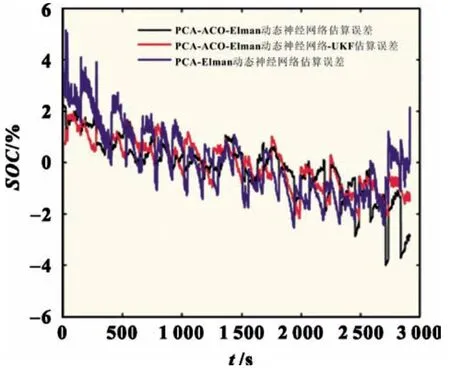
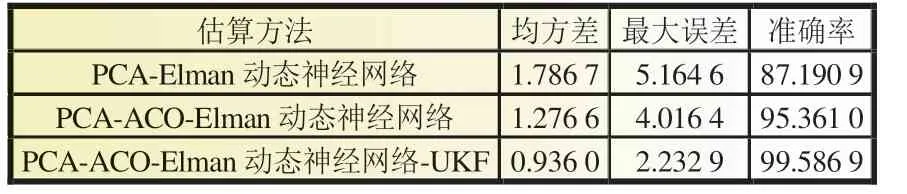
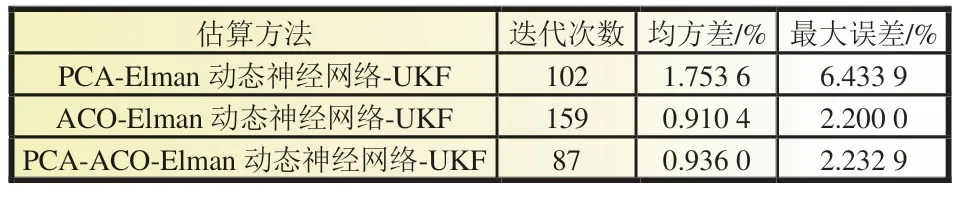
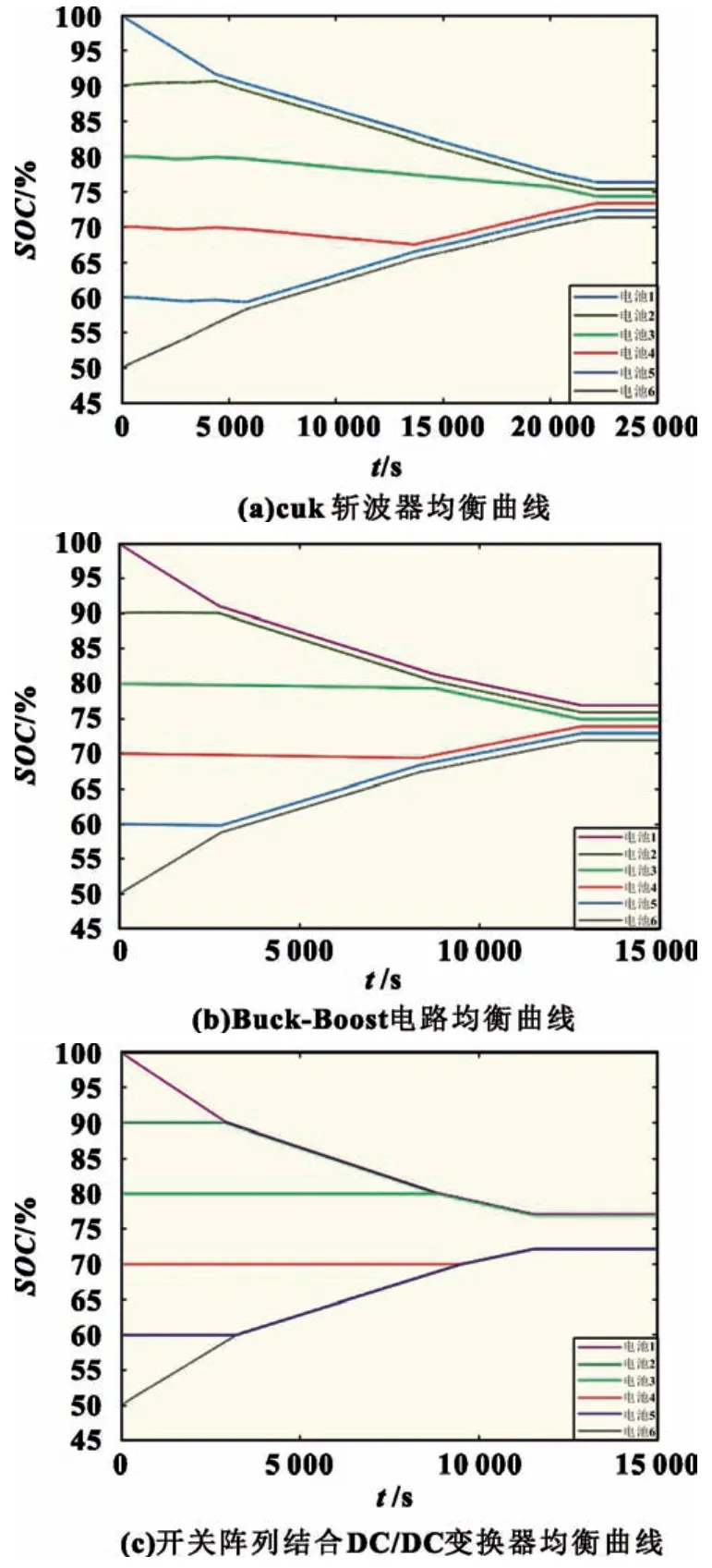
阶段Ⅱ(t1~t2):此阶段为弱电池充电阶段。除M(2,1)继续导通外,PWM 还需控制M(2,6)、M(1,12)、M(1,13)导通,导通时长为t2-t1,L 将阶段Ⅰ储存的能量向B6传递,因电路工作于DCM 模式,故t2-t1 式中:R2为充电回路损耗,包括上述4 个开关的阻抗、电感电阻等。 至t2时刻,电流为0,能量传递结束。 此阶段L 释放的能量为: 综合式(1)~(5)可得,一个均衡周期内的能量转换效率η为W2/W1。 阶段Ⅲ(t2-t3):此阶段为静置阶段,目的是使电感复位可靠,无能量传递。 由图2(b)可知,在能量传递阶段,M(2,1)处于常开状态,在放电阶段,PWM 单元只需对M(1,1)、M(2,8)、M(1,6)输出同步脉冲;同理,在充电阶段,PWM 单元只需对M(2,6)、M(1,12)、M(1,13)输出同步脉冲。因此,确定需要进行充放电的电池后,PWM 控制过程简单。 如图1 所示,M(1,)系列开关为电池选择阵列,其与各电池连接,用于选通对应序号的电池参与均衡;M(2,)系列开关为极性选择阵列,其与储能电感连接,用于控制电流方向,即控制某电池充电或放电;M3 用于防止弱电池对电感反向充电。 当奇数号电池参与均衡时,除导通与其相连的电池选择开关外,若放电,还需导通M(2,1)和M(2,6),若充电,还需导通M(2,3)和M(2,8),其余开关断开;当偶数号电池参与均衡时,除导通与其相连的电池选择开关外,若放电,还需导通M(2,3)和M(2,8),若充电,还需导通M(2,1)和M(2,6),其余开关断开。M(2,2)、M(2,4)、M(2,5)、M(2,7)四个开关分别与上述开关互补,无论什么情况均关断,用于防止上述开关导通时,电流双向流通,开关阵列真值见表1。 表1 开关阵列真值 本文提出PCA-ACO-Elman 动态神经网络-UKF 算法进行SOC 估算,算法流程见图3。首先,由于锂离子电池SOC 影响因素多,造成后续神经网络结构复杂,训练过程繁琐,故本文使用PCA 算法消除影响因素间的相关性,利用有限个主元覆盖原始数据提供的多数信息。然后,将PCA 算法得到的主元输入Elman 神经网络,Elman 神经网络预测不依赖电池模型精度,且具备动态记忆效应,SOC 估算是一个基于时间序列的问题,故可最大化Elman 神经网络的特有功能。为避免Elman 神经网络陷入局部最优,利用蚁群算法的全局寻优能力反复优化神经网络的权值和阈值,训练完毕后,将测试数据的主元导入,即获得网络输出结果。最后,将神经网络输出结果作为观测值输入UKF 滤波器,输出结果为最终预测结果。 图3 算法流程 具体实现过程如下。 (1)对m 个SOC 影响因素进行n 次观测,得到原始数据矩阵x,并进行去均值化处理,得到标准化矩阵X: 式中:x1、x2、……、xm均为SOC 影响因素。 (2)计算X 的协方差阵ΨX,并得到ΨX的特征根λ1≥λ2……≥λa≥0 及其对应的特征向量p1、p2、……、pa。 (3)计算主元ti及其方差贡献率δi,和前i 个主元的累积贡献率μi,ΨX的特征根与δi成正比,故将特征根由大到小排列后,根据预设的累积贡献率阈值,选取前p(p≤a)个主元代替原始自变量。 (4)确定神经网络结构:神经网络的输入变量为PCA 算法确定的主元,输出变量为SOC,隐含层节点个数l 尚无明确算法,故用经验公式确定[11]。 (5)蚁群算法训练神经网络:首先,确定蚁群系统初始参数,每只蚂蚁的搜索范围为[-10,10],间隔为0.01,信息素矩阵为τ0,禁忌素矩阵为J0。然后,在第e 次迭代中,蚂蚁k 第r 次(r≤待优化的权值、阈值总数)搜索从i 至j(i、j 为搜索范围内的某个数据)的概率为: 式中:ak为蚂蚁下一步被允许访问的点的集合。此蚂蚁完成搜索后,还原禁忌素矩阵。待本次迭代完成后,确定神经网络输出最小误差对应的蚂蚁,更新信息素τe。 式中:ρ1为信息素挥发系数,0<ρ1≤1,取ρ1=0.7;ρ2为信息素增长系数,0<ρ2≤1,取ρ2=0.3;Δτe为网络输出最小误差对应的蚂蚁走过路径的信息素。达到最大迭代次数或达到预设训练精度并稳定后,视为ACO 对Elman 神经网络的训练完毕。 (6)确定UKF 状态方程和观测方程。本文利用Ah 计量法进行状态预测,将PCA-ACO-Elman 神经网络的输出值作为观测值,可得: 式中:CN为电池额定容量;W(K)、V(k)分别为过程噪声和测量噪声。 (7)计算sigma 点及其对应权值。 式中:λ 为缩放比例系数,取λ=1;α 控制sigma 点集的分布,取α=1;β 用于合并高阶项的动差,取β=1。 (8)计算状态量的一步预测值和协方差阵,UKF 算法利用一组sigma 点,并对它们加权求均值,得到状态量的一步预测。 (9)再次使用UT 变换,产生新的sigma 点,代入观测方程,得到观测预测值,并通过式(13)加权,得到系统的预测值和协方差。 (10)计算UKF 增益阵,更新状态量和协方差。 本文采用基于SOC 极值和均值的控制方法,即当电池组SOC 极差或各电池SOC 与电池组SOC 均值之差的绝对值超过阈值时,最强电池的能量开始向最弱电池传递;当电池组SOC 极差和各电池SOC 与电池组SOC 均值之差的绝对值同时低于阈值时,均衡停止[12]。 均衡开启条件: 式中:λ1、λ2为均衡开启阈值,只要满足上式任意一个条件,均衡即开启。 均衡结束条件: 式中:λ3、λ4为均衡结束阈值,只有同时满足上式两个条件,均衡才结束。 均衡流程见图4,具体步骤如下。 图4 均衡流程 (1)应用电压传感器、温度传感器等专业仪器测量电池组原始数据,并根据第2 节中的算法进行SOC 估算,计算电池组SOC 均值,判断最强电池和最弱电池。 (2)判断电池组是否满足均衡开启条件,若满足,则转至(3);若不满足,则均衡不开启。 (3)PWM 对相应MOSFET 开关输出周期性脉冲,使最强电池的多余能量向最弱电池传递,此过程持续1 min 后,进行SOC 估算,计算电池组SOC 均值,判断最强电池和最弱电池,并判断是否满足均衡结束条件,若满足,则均衡结束;若不满足,则重复(3)。 本文的实验对象为某公司生产的电动公交车用电池包,该电池包由174 节18650 锂电池串联组成,单体标称电压为3.36 V,容量为2.4 Ah,故电池包标准输出电压为582 V,能量为1.4 kWh,在充放电测试仪上进行两组充放电实验,采集周期为1 s。第一组以0.75 C 放电4 713 s,静置1 834 s 后,又以0.5 C 充电2 160 s,共计8 707 组数据,作为训练数据;第二组以0.5 C 充电2 911 s,共计2 912 组数据,作为测试数据。 本文选取的初始自变量分别为电压、电流、温度、电池寿命、充放电循环次数、电池管理系统(BMS)使用寿命、电池管理单元(BMU)使用寿命,经PCA 算法处理后,将输出数据代入式(8),结果见表2。 表2 PCA 算法结果 由表2 可得,前4 个主元累积贡献率超95%,可近似认为包含原始数据全部信息,第5~7 个主元总权重不足4%,可忽略,故选取累积贡献率达到90%的前4个主元作为Elman 神经网络的输入自变量,网络输入节点为4 个,输出节点为1 个。根据经验公式(11)确定神经网络的隐含层节点个数,初选节点个数为3~12 个,故选取4、6、8、10、12 个节点进行仿真,利用ACO 对网络进行训练,设置最大迭代次数为100,蚂蚁为3 000只,训练完成后,将测试数据输入网络,结果见表3。 表3 节点个数的对应误差 经综合考量,选定隐含层节点个数为10 个,因此,ACO算法需优化的权值和阈值的个数分别为50 和11 个。ACO 将网络训练完毕后,将测试数据输入,神经网络输出结果后,将其输入UKF 模型。本文选取PCA-Elman 神经网络估算和PCA-ACO-Elman 神经网络估算方法与上述方法进行对比,对比曲线见图5,误差曲线见图6,将误差绝对值小于2%的时刻设为正确值,结果见表4。 图5 SOC估算结果对比 图6 误差曲线 表4 算法结果对比 % 对比图5(a)、(b)和图6 可得,在多数时刻,PCA-Elman 神经网络输出结果变化趋势与实际值不符,此现象在充电开始和结束阶段表现明显,而PCA-ACO-Elman 神经网络输出曲线在前期的跟随性较好,但随着充电进行至2 000 s 开始,误差累积造成后期误差剧增,故虽然ACO 具有良好的全局寻优能力,但无法解决误差曲线在后期波动剧烈的问题,在电动汽车运行过程中,会造成续驶里程计算错误,影响汽车行驶安全,且造成电池使用寿命下降。 对比图5(b)、(c)和图6 可得,PCA-ACO-Elman 神经网络经UKF 滤波后,估算曲线变化的总体趋势与实际相符,误差曲线变化平稳,具备良好的收敛性,无突变剧烈现象,误差维持在1%左右。因此,本文提出的估算方法精度高,且稳定性较好。 本文提出PCA-ACO-Elman 动态神经网络-UKF 联合算法的前期Elman 神经网络训练在离线状态进行,为验证此算法在保证高精度的同时又可提升计算速度,即降低算法的训练复杂程度,将其与PCA-Elman 神经网络-UKF 算法、ACOElman 神经网络-UKF 算法的训练迭代次数和测试精度进行对比,结果见表5。 表5 计算速度对比 由表5 可得,ACO 算法的全局寻优能力使算法精度提高的同时,计算速度小幅提升;PCA 算法的加入使系统输入变量维数减小,故迭代次数显著下降,且估算精度的下降量极小可近似忽略。因此,本文提出的PCA-ACO-Elman 动态神经网络-UKF 联合算法可以同时兼顾精度和速度。 为保证此算法在单片机的实现,作者在MPLAB IDE(PIC单片机的程序编译环境)中编译代码,共有223 条指令,PIC18系列单片机是外部晶振模式,晶振频率为10 MHz,故指令周期为1×10-7s,单次估算时长约为2.23×10-5s,而SOC 采集周期为1 s,因此用单片机可以实现该算法。 本文在Matlab/Simulink 2018a 的Simscape Power Systems平台下构建均衡模型,通过检测各电池SOC 的变化以验证该均衡方案的优越性,选定6 节串联的标称电压为3.3 V、容量为2.4 Ah 的磷酸铁锂电池为研究对象,初始SOC 分别为100%、90%、80%、70%、60%、50%。电感值设为1 mH,电感直流电阻设为0.75 Ω,PWM 输出脉冲频率为1 kHz,导通占空比为0.35。MOSFET 开关导通压降设为0.1 V,阻抗为0.05 Ω。根据国家标准和本文的SOC 估算误差,同时为防止开关频繁开闭,将第3 节中的均衡开启和结束阈值设置为λ1=10%,λ2=3%,λ3=8%,λ4=2.5%。将所提出的均衡方案与传统DC/DC 变换器和cuk 斩波器进行对比,其中传统DC/DC 变换器选用双向Buck-Boost 电路,二者的均衡能量传递方式均为相邻单体-单体形式,即满足均衡开启条件时,强电池开始向相邻的弱电池放电,直至满足均衡结束条件为止,二者的电池参数、电感值、电感直流电阻、PWM 输出脉冲频率及占空比、MOSFET开关参数与上述一致,cuk 斩波器的电容值设为1 mF,且为保证均衡时间和效率对比的合理性和公平性,均衡开启和结束条件与本文方案相同,对比曲线见图7,结果见表6,表6 中均衡效率的计算方法为:各电池均衡过程中释放或吸收的总体能量通过公式W=∫i(t)u(t)dt 确定(电流>0 充电,电流<0 放电),故W>0,该电池均衡过程中吸收能量,W<0,该电池释放能量,将吸收能量的电池的W 和释放能量的电池的|W|分别相加,得到∑W(W>0)和∑|W|(W<0),∑W/∑|W|即为总体均衡效率。 图7 均衡对比曲线 表6 均衡对比结果 对比图7(a)、(b)和表6 可得,在均衡后电池组SOC 极差相同和各电池SOC 与电池组SOC 均值之差的绝对值低于阈值的条件下,双向Buck-Boost 电路的均衡时间比cuk 斩波器缩短9 016 s,均衡效率高5.07%。结果表明:与双向Buck-Boost电路相比,cuk 斩波器均衡曲线的升降斜率小,即回路电流较小,单次能量传递能力较弱,故能量传递周期长,开关损耗、回路电阻等造成的能量损失剧增,导致均衡效率下降,在电池SOC 相差较大和能量传递路径较远的情况下表现明显。 对比图7(b)、(c)和表6 可得,在均衡后电池组SOC 极差相同和各电池SOC 与电池组SOC 均值之差的绝对值低于阈值的条件下,本文提出的开关阵列结合DC/DC 变换器的均衡时间比双向Buck-Boost 电路缩短1 552 s,均衡效率高4.96%。结果表明:开关阵列使能量传递方式更直接,即传递路径更短,不再局限于相邻单体,均衡后期的最强电池和最弱电池数量均增多,即参与充放电的电池增多,回路电流成倍上升,能量传递能力增强,且由于均衡电路工作时,PWM 只需对1~4 个开关输出同步脉冲,能量传递回路的其余开关常开,即可实现能量在任意电池间传递,因此开关损耗较小,故均衡效果较好。 针对锂离子电池组使用中的不一致问题,本文提出以SOC 为变量的均衡方案。对于SOC 估算,设计PCA-ACOElman 动态神经网络-UKF 的SOC 联合估算方法,使用PCA 对数据降维,并利用ACO 全局寻优能力优化神经网络的权值和阈值替代依赖模型辨识精度的传统Kalman 滤波器,将Ah 计量法公式应用在UKF 状态方程上对神经网络输出结果进行滤波;对于均衡电路,本文设计基于开关阵列的双向DC/DC变换器电路,并以SOC 极值和均值为均衡开启和结束条件。通过实验及仿真分析,此均衡方案的估算误差小、稳定性好、无误差剧烈突变现象、计算速度快,且在改进电池组不一致性的同时,均衡时间短、效率高,避免传统DC/DC 变换器能量传递的局限性,故整体效果较好。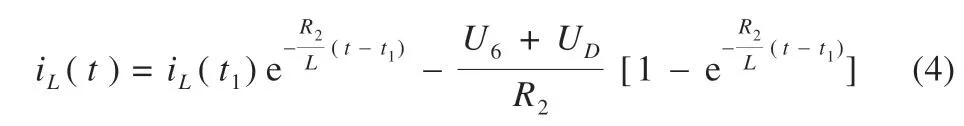
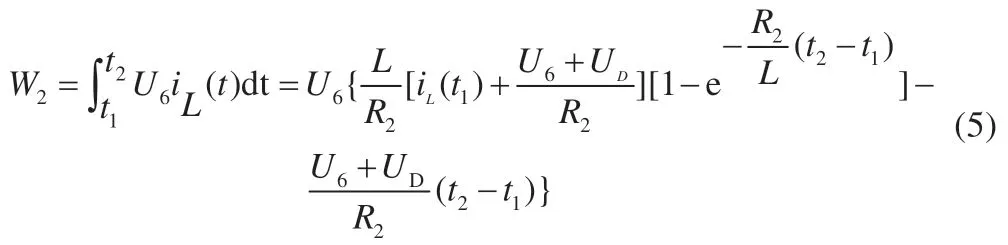
1.3 开关阵列
2 SOC 估算

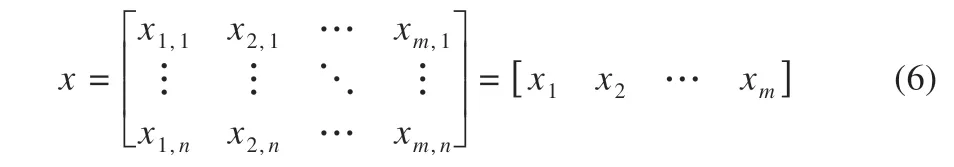
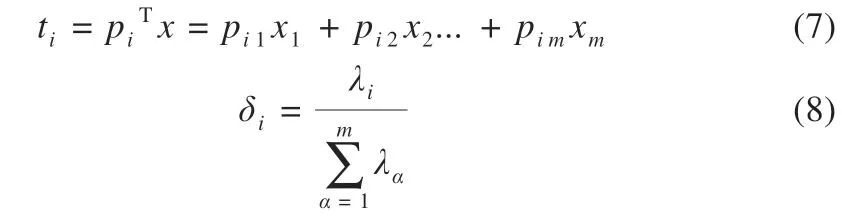


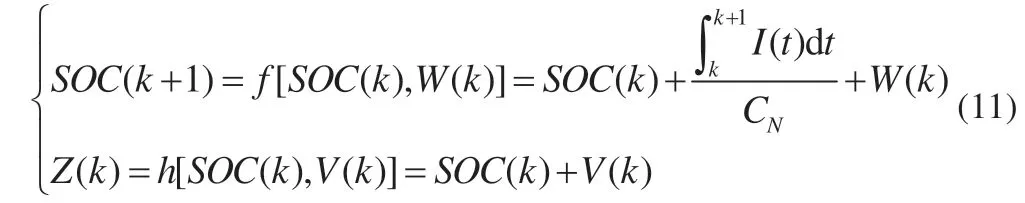
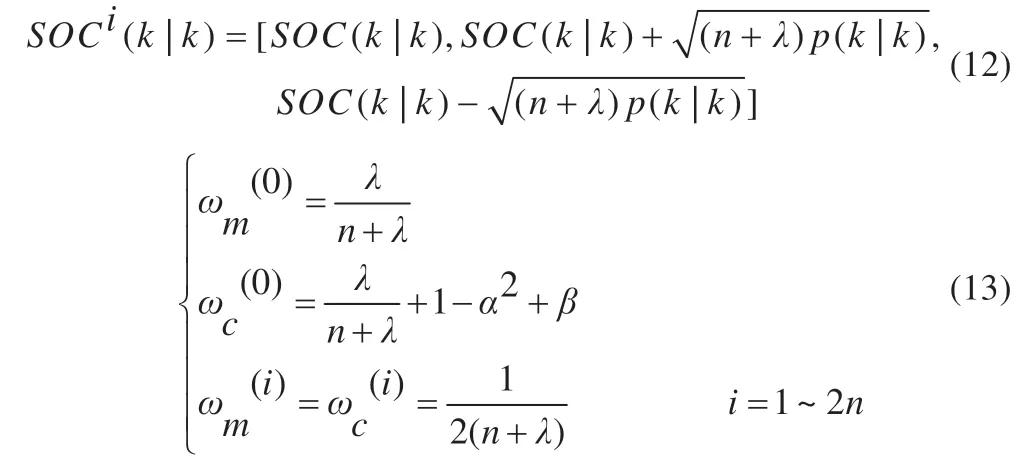
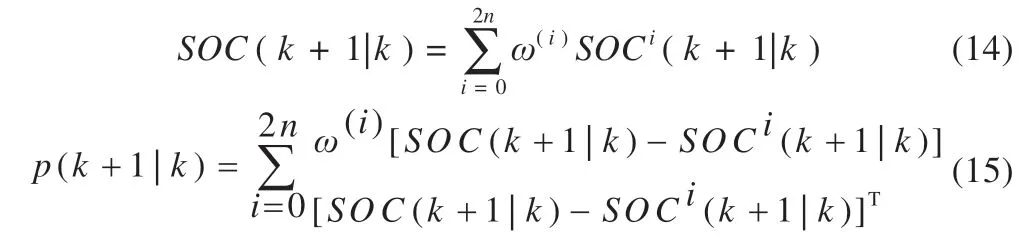
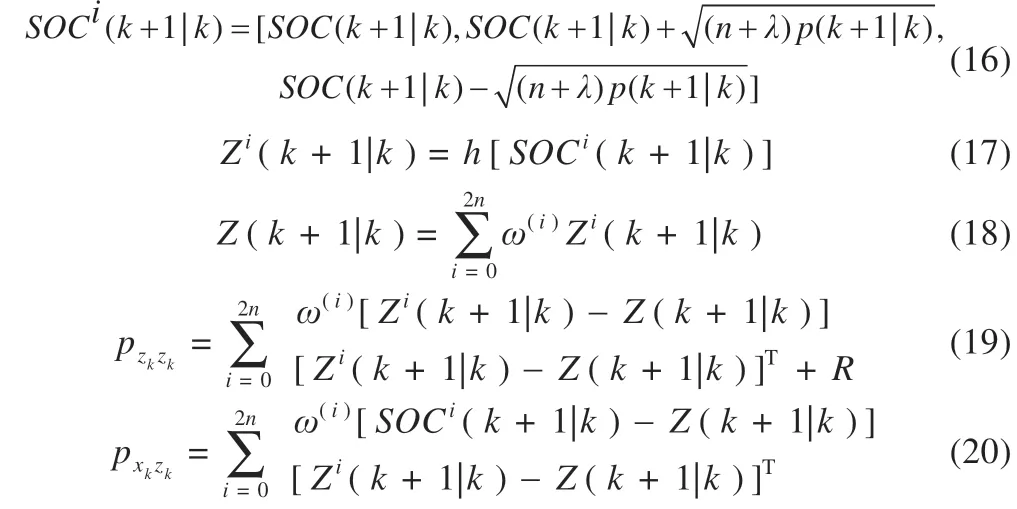
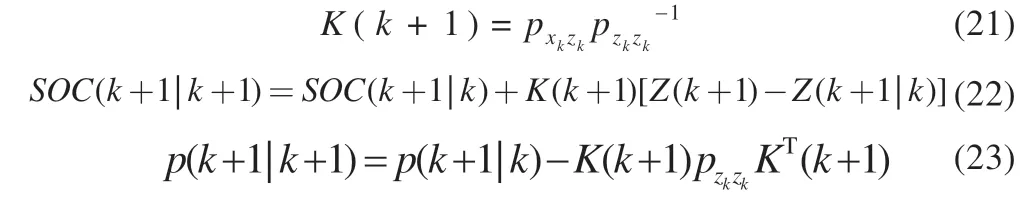
3 均衡方法研究
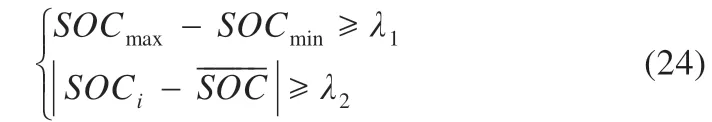
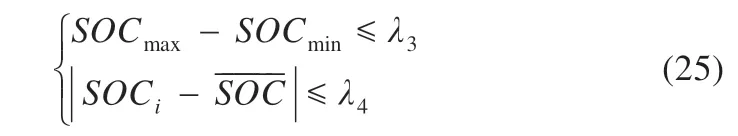
4 实验与仿真分析
4.1 SOC 估算效果分析

4.2 均衡效果分析

5 结语
