先简支后连续混凝土梁负弯矩区UHPC“T形”湿接缝试验研究
2021-04-02邵旭东孔小璇邱明红陈玉宝
邵旭东,孔小璇,邱明红,陈玉宝
(湖南大学土木工程学院,湖南长沙 410082)
与简支梁桥相比,先简支后连续混凝土梁桥受力更加均匀,行车更为平顺舒适,因此应用广泛[1-7].然而,在正常使用状态下,其墩顶负弯矩湿接缝处承受着较大的负弯矩和剪力,是先简支后连续混凝土梁桥的设计控制截面[2].已有工程实践表明[2-8],由于车辆超载、疲劳受荷等原因,一些运营中的先简支后连续梁桥在其湿接缝的桥面板处过早地出现了一些沿桥纵向和横向的裂缝,而这些裂缝对桥梁的受力性能和耐久性造成了相当不利的影响,负弯矩湿接缝开裂也成为先简支后连续混凝土梁桥最典型、最常见的问题.
为解决上述问题,已有学者从预应力布置、湿接缝材料和湿接缝构造形式等方面开展相关研究工作,以期改善其受力性能与耐久性.传统负弯矩湿接缝构造通过张拉墩顶预应力束来限制负弯矩区的裂缝发展.由于施工面狭窄、高空作业困难等问题,墩顶预应力束施工复杂且施工质量低,由此导致的湿接缝实际构造情况难以达到设计预期效果[9-13].吕佳元等[12]、周建庭等[13]提出了一种新型的负弯矩区段构造来解决简支变连续预应力混凝土梁桥中预应力损失过大、主梁严重开裂等问题,但其增大了桥梁的自重和现场的焊接量;传统墩顶湿接缝构造材料采用高强微膨胀混凝土[2],为了提高接缝的抗拉、抗裂强度,有部分学者[7,14]提出使用高强钢纤维混凝土来代替传统的普通高强微膨胀混凝土来改善湿接缝的受力性能.梁明元等人[2]认为钢纤维高性能混凝土材料对湿接缝性能的改善效果并不明显,因此引入强度高、韧性大的超高韧性混凝土(Ultra High Toughness Concrete,简称UHTC)来代替传统湿接缝采用的高强微膨胀混凝土,然而其接缝结构中仍采用了墩顶预应力束,仍会由于预应力的存在而增加施工难度、降低施工质量;传统墩顶湿接缝通常采用矩形构造形式,这种构造形式使得现浇接缝与预制梁段的界面处于高应力区,极易开裂.张阳等人[15]对比矩形、楔形及菱形3种接缝截面形式对接缝板界面开裂强度的影响,结果表明除矩形接缝形式外其余接缝形式均能提高接缝界面的开裂强度,其界面仍处于受拉高应力区,只是提高了界面处结合面的咬合能力.
综上,本文提出一种超高性能混凝土新型湿接缝构造.超高性能混凝土(Ultra High Performance Concrete,UHPC)是一种新型纤维增强水泥基复合材料,具有优异的力学性能和耐久性能且裂后的延性和韧性较好[16-18].将UHPC应用于接缝结构,有望大幅提高其抗拉、抗裂性能,取消用于墩顶抗裂的负弯矩束,且利用UHPC与钢筋间良好的锚固性能来取消接缝内钢筋间的焊接[19],简化施工.为探究取消墩顶预应力束、取消钢筋焊接的UHPC新型湿接缝在工程应用中的可行性,本文对提出的负弯矩区UHPC新型湿接缝构造进行配筋试设计,并对其开展1 ∶2缩尺模型试验研究.
1 UHPC湿接缝设计方案
1.1 “T形”湿接缝概念设计
由于传统湿接缝构造存在负弯矩区预应力束张拉困难和钢筋焊接费时的问题,本文基于UHPC材料优异的抗拉性能、与钢筋的高握裹性能和耐久性能提出适用于先简支后连续混凝土梁桥的UHPC“T形”湿接缝方案,该方案如图1所示.方案中的“T形”构造指的是墩顶负弯矩区现浇UHPC的覆盖长度大于横梁的形式.该方案具有以下优势:
1)UHPC层的覆盖能降低湿接缝构造内受拉钢筋的应力,尽管没有负弯矩预应力束也能有效限制负弯矩桥面板顶面的裂缝宽度,且UHPC与普通混凝土(Normal Concrete,简称NC)的竖向交界面由于“T形”构造而远离负弯矩高应力区,使得竖向交界面不至于过早开裂.
2)UHPC由于超低水灰(胶)比和高胶凝材料用量,早期收缩发展较快且总收缩高于普通混凝土或高性能混凝土,而“T形”接缝构造阻滞了UHPC的收缩,减小了竖向交界面内由收缩约束产生的初始拉应力.
3)UHPC具有优异的特性,有望取消传统湿接缝构造负弯矩预应力束和钢筋的焊接,因而能解决因狭窄工作面而引起的施工质量差的问题,以及因钢筋焊接引起的施工复杂、施工周期长的问题.
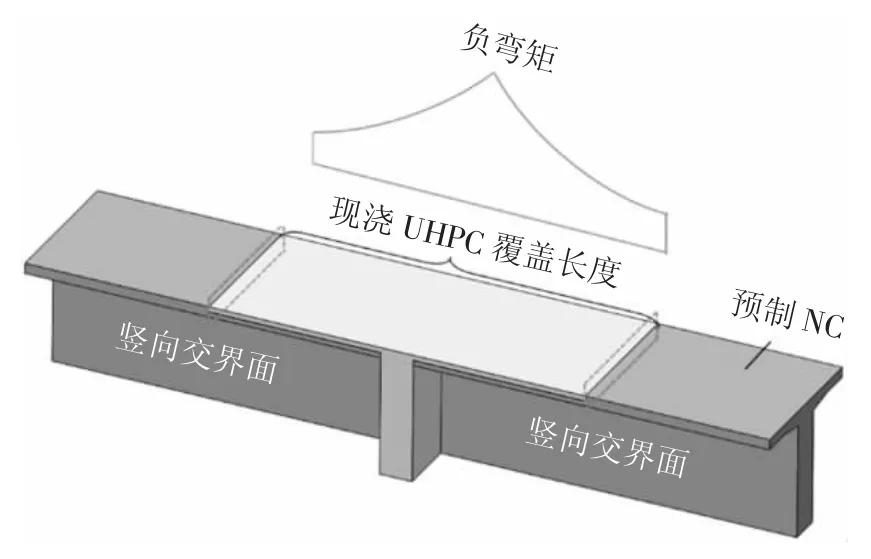
图1 UHPC新型湿接缝构造示意图Fig.1 UHPC new wet joint structure diagram
1.2 整体计算
本文以某跨径布置为5×30 m的普通混凝土先简支后连续预制T梁为背景,采用UHPC新型湿接缝的设计方案,预制段采用强度等级为C50的NC.该桥宽为16.25 m,梁高2 m.现浇UHPC“T形”湿接缝翼缘沿桥纵向的长度为5.8 m,高度为0.08 m,其腹板沿桥纵向的长度为0.5 m,高度为1.92 m,方案具体尺寸如图2所示.
采用MIDAS/Civil软件建立背景桥例的有限元模型,模型中,“T形”接缝外伸段与预制NC梁形成的组合截面段采用联合截面,其截面特性中基本材料为UHPC.模型主要考虑恒载、汽车活载、温度荷载、支座沉降、预应力、收缩徐变等荷载和作用,其中汽车活载为公路-Ⅰ级车道荷载.
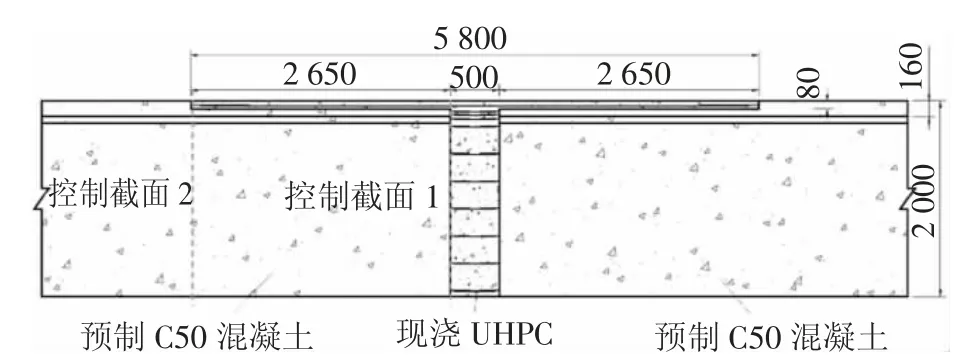
图2 NC连续梁桥负弯矩区UHPC新型湿接缝方案(单位:mm)Fig.2 UHPC newtype wet joint scheme for normal concrete beam bridge(unit:mm)
根据《公路桥涵设计通用规范》(JTG D60—2015)和《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[20]要求,对背景工程按正常使用极限状态和承载能力极限状态分别进行荷载组合,重点关注两个关键截面(如图2所示)的弯矩及其顶面应力,计算结果见表1.
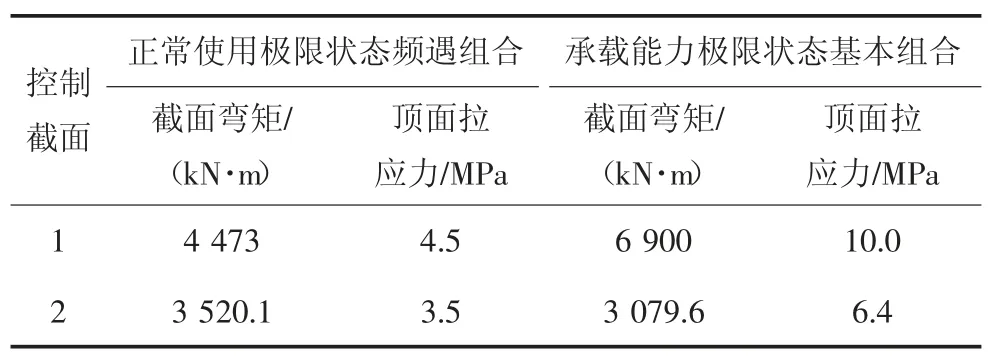
表1 整体计算结果Tab.1 Overall calculation results
1.3 试验配筋设计
本文通过MATLAB数值模拟来控制1.2节所述控制截面在设计应力下的裂缝宽度来进行配筋设计.据相关研究[21-22],当UHPC的裂缝宽度不超过0.05 mm时对其耐久性没有影响,因此计算配筋时控制UHPC裂缝宽度为0.05 mm,其裂缝宽度的计算基于法国UHPC结构设计规程[23];UHPC覆盖下的NC的控制裂缝宽度按规范取值,由《公路钢筋混凝土及预应力混凝土桥涵设计规范》[20]可知,正常使用极限状态下,一般环境中的钢筋混凝土构件的最大裂缝宽度为0.2 mm.
计算控制裂缝宽度下的配筋面积是一个迭代计算的过程,通过迭代曲率来得到控制裂缝宽度下截面弯矩和配筋面积的关系式,最终得到满足正常使用极限状态的裂缝宽度要求下控制截面1处NC层的最小配筋面积.计算时,控制截面1和控制截面2分别偏安全地按UHPC-NC组合截面和全NC截面计算.参考文献[24]中UHPC桥面板内钢筋的布置,拟定UHPC层内钢筋等级为HRB400,直径为20 mm,间距为100 mm.MATLAB程序中偏安全地忽略预应力筋对截面轴向平衡的影响,其具体计算示意图和流程图分别如图3和图4所示.采用的各材料的本构关系如图5所示,其中UHPC仅受拉,其单轴抗拉强度ftu参考《钢-超高韧性混凝土轻型组合结构桥面技术规范》(DB43/T 1173—2016)[25]取7 MPa,弹性模量为42 GPa;C50的单轴抗拉本构参考文献[26],其单轴抗拉强度ftd取1.89 MPa,单轴抗压本构参考《混凝土结构设计规范》(GB 50010—2010)[27],其单轴抗压强度fcd取32.4 MPa,弹性模量取34.5 GPa;钢筋的拉压本构关系参考文献[26],其屈服强度fy取420 MPa,弹性模量Es取200 GPa,Es′=0.01Es.
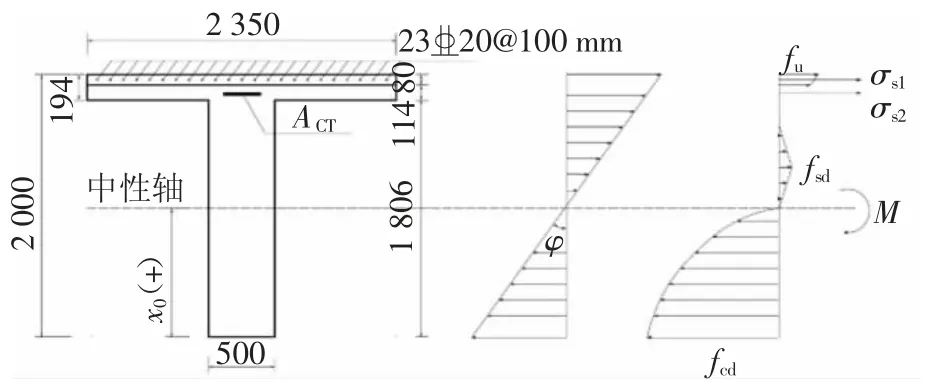
图3 配筋面积计算示意图(单位:mm)Fig.3 Reinforcement area calculation diagram(unit:mm)
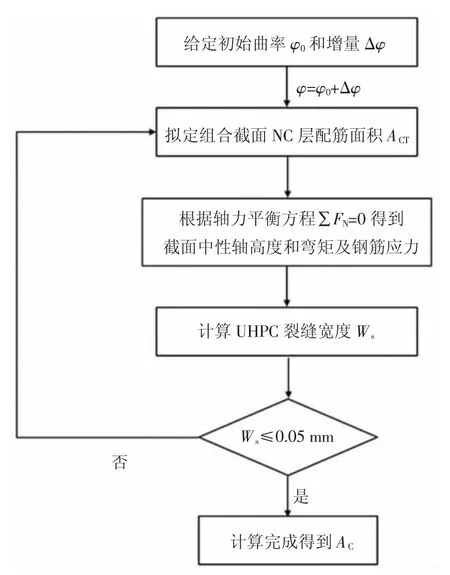
图4 配筋面积计算流程图Fig.4 Reinforcement area calculation flowchart
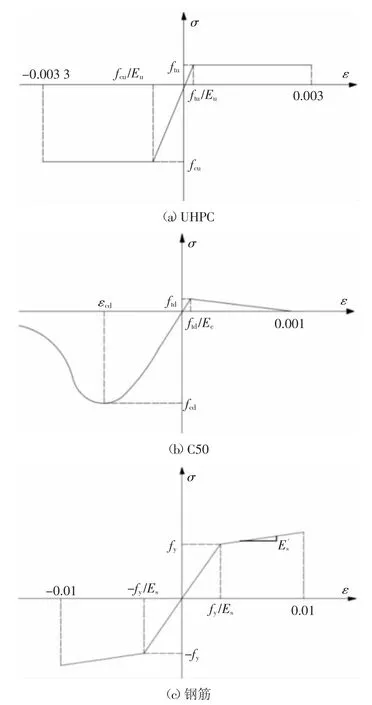
图5 材料本构关系图Fig.5 Material constitutive diagram
经计算,控制截面1处NC层的最小配筋面积为1 500 mm2(约为12根直径为14 mm的钢筋),偏安全地统一UHPC层和NC层钢筋直径,大小为20 mm.此时控制截面1处UHPC顶面的裂缝宽度为0.03 mm,NC顶面的裂缝宽度为0.05 mm,满足设计要求;控制截面2的钢筋面积和布置形式均与控制截面1相同,在此配筋下,设计应力时控制截面2处NC顶面的裂缝宽度为0.061 mm,也满足设计要求.因此控制截面1和控制截面2内配筋形式见表2.

表2 控制截面初步配筋形式Tab.2 Control section preliminary reinforcement form
2 普通混凝土梁负弯矩区UHPC接缝缩尺模型试验
2.1 试件设计
为了研究上述负弯矩区UHPC新型湿接缝构造的可行性,按与背景桥例中两个控制截面应力等效的原则对其进行1 ∶2的缩尺设计.模型相似关系见表3.

表3 模型与实桥物理相似关系Tab.3 Physical similarity between model and real bridge
试验模型全长5.74 m,计算跨径为5.54 m,宽1.175 m,梁高1 m,翼缘板厚度0.08 m.现浇UHPC“T形”接缝翼缘沿纵向的长度为2.9 m,高度为0.04 m,“T形”接缝腹板沿纵向的长度为0.25 m,高度为0.96 m.纵筋的配筋率不变,全梁段配筋相同,受拉区均采用双层配筋,上层布置16根直径为12 mm的钢筋,间距为70 mm;下层布置8根直径为12 mm的钢筋,间距为140 mm;受压纵筋为3根直径为16 mm的钢筋,间距为80 mm.纵筋的形心距为原桥的1/2.该缩尺模型构造如图6所示.
试验模型预制部分采用C50混凝土材料,现浇UHPC内钢纤维采用直径为0.12 mm,长度为8 mm的直纤维,体积掺量为2.5%.钢筋等级为HRB400.T梁预制部分浇筑完成并养护28 d后对界面使用电镐进行凿毛处理.凿毛时尽量使得粗骨料部分露于表面,完成后用清水洗净.为了保证界面的黏结强度,在界面湿润的状态下浇筑UHPC,自然养护2个月后进行模型试验.
浇筑试件时制作3个150 mm的C50立方体试块、3个150 mm×150 mm×300 mm、6个150 mm×150 mm×400 mm的C50混凝土棱柱体试块和6个100 mm的UHPC立方体试块、6个100 mm×100 mm×300 mm、6个100 mm×100 mm×400 mm的UHPC棱柱体试块.与试件同条件养护,养护完成后按标准试验方法测得C50混凝土和UHPC的基本力学性能如表4所示;纵向受拉主筋的实测屈服强度为430 MPa,极限抗拉强度为578 MPa,弹性模量为195.6 GPa.
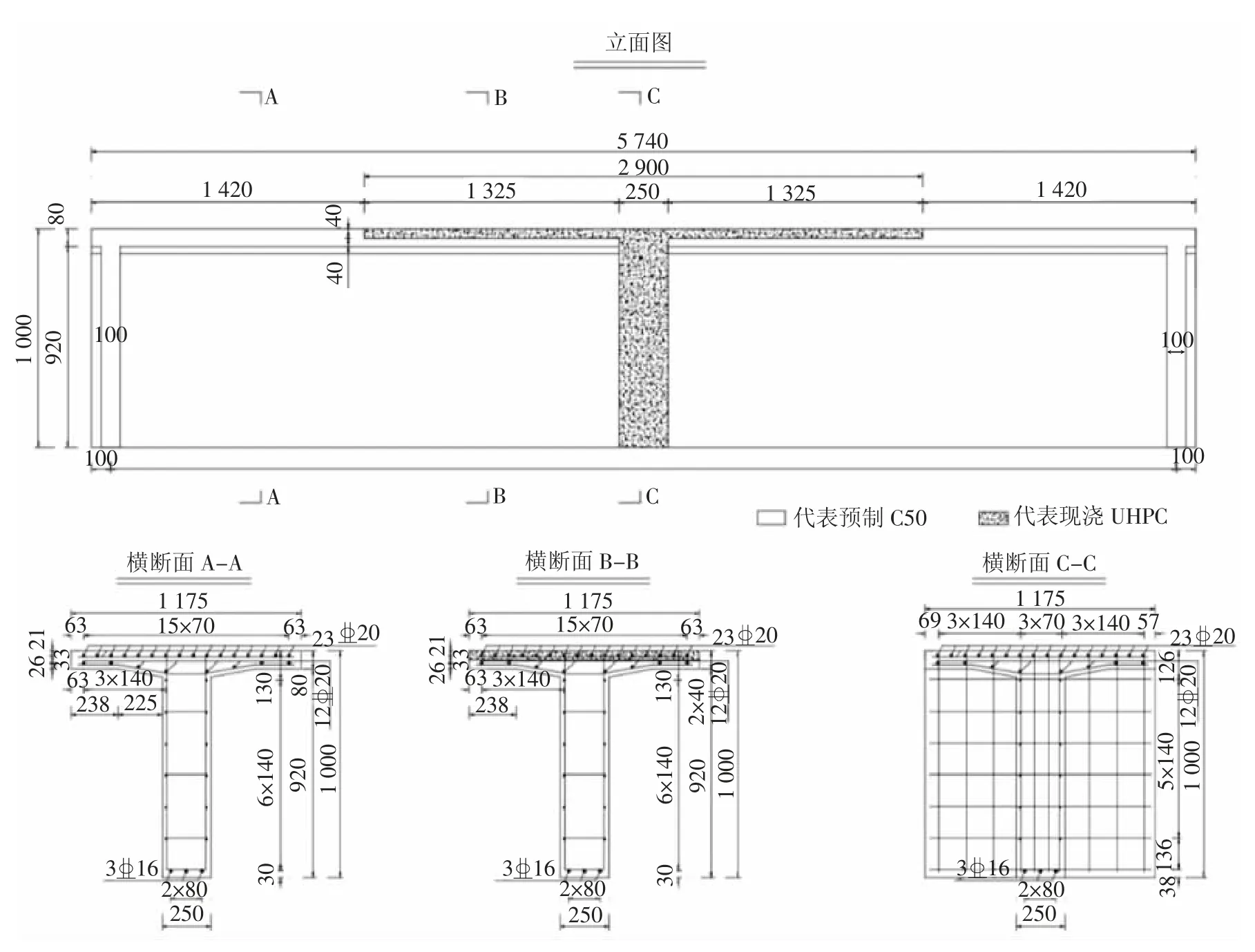
图6 试验模型构造图(单位:mm)Fig.6 Test model construction diagram(unit:mm)
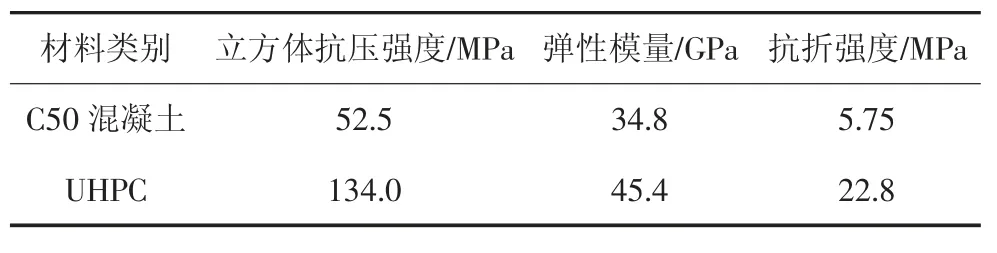
表4 混凝土材料基本力学性能Tab.4 Basic mechanical properties of concrete materials
2.2 试验加载及量测方案
考虑到正弯矩试验更方便操作,故将图6试验模型翻转,变负弯矩试验为正弯矩试验,采用MTS四点弯曲加载,试验梁和分配梁的边界条件均为简支.模型设计及加载方式遵循以下原则:在正常使用极限状态频遇组合下,保证负弯矩区控制截面(图2中的控制截面1和控制截面2)的应力比和试验正弯矩区控制截面(图7中的截面D/F和B/H)的应力比相等,这样便于知晓今后实桥截面的开裂顺序.背景桥例的应力计算考虑了先简支后连续分期受力的影响.试件开裂前采用力加载,加载步为25 kN,开裂后采用位移控制加载.试验模型的纯弯段长度为1.34 m.加载装置及仪表布置如图7所示,试验选取9个截面(图7中A~I截面)测量沿梁高的应变分布,应变片布置如图8所示.为了较为准确地量测各截面裂后混凝土的应变分布,在9个截面顶、底面均布置有量测应变的引伸仪.选取7个测点测量试验梁的竖向位移,同时采用千分表测量UHPC和NC的层间滑移,并记录荷载作用下裂缝长度和宽度的发展情况.实际试验加载如图9所示.
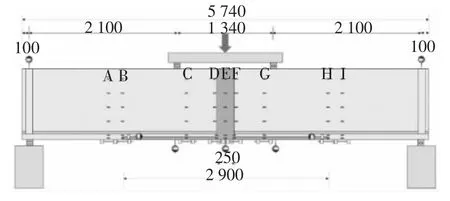
图7 试验梁加载装置及测量仪器布置图(单位:mm)Fig.7 Test beam loading device and measuring instrument layout(unit:mm)

图8 侧面、底面、顶面应变片布置图(单位:mm)Fig.8 Side,bottom,top strain gage layout(unit:mm)

图9 实际试验加载图Fig.9 Actual test loading diagram
3 MATLAB程序及试验结果分析
3.1 缩尺模型MATLAB程序编制
本文采用MATLAB程序对上述缩尺模型试件不同截面的弯矩-曲率曲线和试件梁的荷载-变形曲线进行数值模拟,并与试验值对比.一方面验证前述试验梁配筋试设计的合理性;另一方面,为后续采用该MATLAB程序进行参数分析提供可靠支撑.
3.1.1 负弯矩截面弯矩-曲率
假定截面均满足平截面假定,试验梁截面的弯矩-曲率(M-φ)全曲线应力应变计算示意图如图3所示,具体的计算流程见图10,计算时以受拉为负,受压为正.程序中,UHPC的受压本构关系参考文献[28].其余各材料的拉压本构关系与图5相同,本构中各参数的取值均参照表4中的材性试验结果.
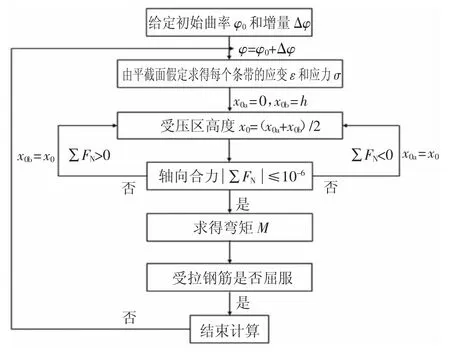
图10 截面弯矩-曲率曲线编制流程图Fig.10 Flow chart for compiling section bending momentcurvature curve
3.1.2 缩尺模型试件的荷载-跨中位移曲线
在求解梁的变形时,可以采用共轭梁法计算任意截面处的转角和挠度.为求解模型试件的荷载-跨中位移曲线,读入已计算完成的试验梁各截面的Mφ 曲线,控制最不利截面的破坏条件,最终得到试验梁的荷载-跨中位移曲线.具体的程序编制流程图如图11所示.
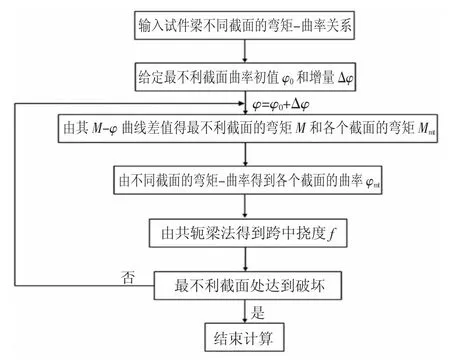
图11 构件荷载-跨中挠度曲线编制流程图Fig.11 Flow chart of component load-span mid-deflection curve
3.2 试验结果分析
3.2.1 应变分布及滑移
各级荷载下沿梁高方向的应变分布如图12所示.选取试件受压底缘高度处为图中纵坐标原点.试验表明,模型开裂前,平截面变形关系表现良好;模型开裂后,由于开裂截面的应变显著大于未开裂截面,因而应变沿梁高分布出现转折现象.当荷载超过589.1 kN时,受拉翼缘裂缝和腹板斜裂缝的延伸和扩展,使得大部分腹板受拉区应变片因为裂缝穿过而损坏,因此图中未给出荷载超过589.1 kN时对应的沿截面梁高方向的应变分布.


图12 各截面应变沿梁高分布图Fig.12 Strain distribution along the beam height at each section
由图7中B(I)截面处测量UHPC和NC界面滑移的千分表可知,极限荷载时,UHPC和NC界面间的最大滑移为0.031 mm,结合各截面应变沿梁高的分布可知该UHPC与NC间有良好的协同作用.
3.2.2 荷载-位移曲线
梁跨中挠度计算值为跨中位移的测量值与两支座挠度平均值之差.试件梁的实测荷载-梁顶面跨中挠度曲线与MATLAB的数值模拟结果对比如图13所示,数值模拟曲线仅考虑到钢筋初始屈服点之前.由图13可看出,试验值与模拟值在大约550 kN之前吻合良好,验证了数值模拟中材料参数选取的准确性和适用性.后期存在差异的原因主要有两个:第一,当荷载达到536.2 kN时,试验梁在剪弯段腹板上出现斜裂缝,斜裂缝的产生使得试验梁跨中位移增加;第二,UHPC开裂后,裂缝处的钢筋应力显著增大,而数值模型中未考虑开裂截面黏结滑移对钢筋应力的影响.
由图13可知,试件的受力可分为3个阶段.1)弹性阶段:试件受拉区未出现裂缝,荷载与挠度呈直线关系,刚度基本保持不变.2)裂缝发展阶段:预制部分NC出现第一条肉眼可见的裂缝,随着荷载的增加,在UHPC-NC组合截面与全NC交界面、UHPC覆盖下的NC侧面和UHPC顶面依次出现裂缝,随着UHPC出现肉眼可见的裂缝,此阶段出现第二个拐点.随着裂缝长度和宽度不断增加,结构刚度不断减小.3)屈服阶段:继续加载,荷载-挠度曲线出现新的拐点,受拉钢筋不断屈服,裂缝宽度迅速增加,试件刚度继续降低,最终界面处裂缝左右由于剪切作用出现一定程度的错台并发展为最宽主裂缝,试件破坏.
表5是UHPC裂缝宽度W=0.05 mm(肉眼可见裂缝)和W=0.10 mm时对应的荷载和控制截面受拉顶面应力以及承载能力极限状态下控制截面对应的荷载和顶面名义应力,其中UHPC裂缝宽度为0.10 mm是其在正常使用极限状态下对应的最大裂缝宽度,该值按法国UHPC结构设计规程[23]中对存在干湿交替的桥梁上部结构的裂缝宽度限值取用.

表5 设计控制截面主要试验结果Tab.5 Design test results of main control sections
3.2.3 裂缝发展
试验过程中对试验梁的裂缝发展进行记录并测量不同荷载下的裂缝宽度.最终的裂缝分布图如图14所示,图中深色部分代表材料UHPC,白色部分代表材料NC.区域QC代表NC预制段,区域JC代表UHPC-NC交界面,区域FC代表UHPC覆盖下的NC,区域FU代表覆盖在NC上的UHPC,区域QU代表全UHPC截面区域.当荷载达到463 kN时,在QC区域出现第一条肉眼可见的裂缝,随后在JC区域、FC区域和FU区域依次出现裂缝,QU区域未发现裂缝.当荷载达到536.2 kN时,NC预制段的腹板上开始出现斜剪裂缝,随着荷载的增大,其裂缝宽度发展较慢.最终试验梁上形成3条主裂缝(如图14(a)中α、β、γ 处).试验梁各个区域的弯矩-最大裂缝宽度曲线的试验值和计算值对比如图15所示.计算裂缝宽度时,不同弯矩下的钢筋应力由3.1节所述程序迭代求解,再通过钢筋应力求解裂缝宽度.UHPC和NC裂缝宽度的求解分别基于法国UHPC结构设计规程和文献[20]中的裂缝宽度计算公式.由图15可知,各区域最大裂缝宽度的试验值与计算值拟合良好,为后续抗裂分析提供了依据.
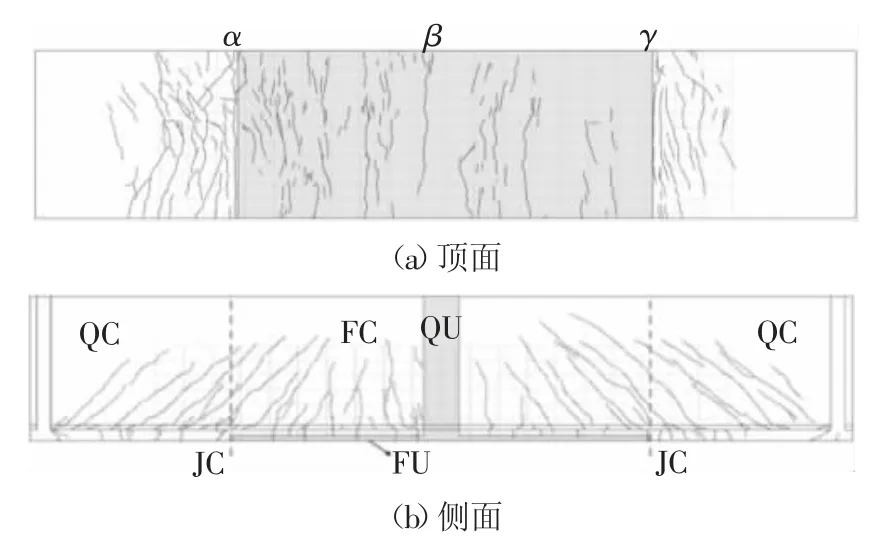
图14 裂缝分布图Fig.14 Crack map
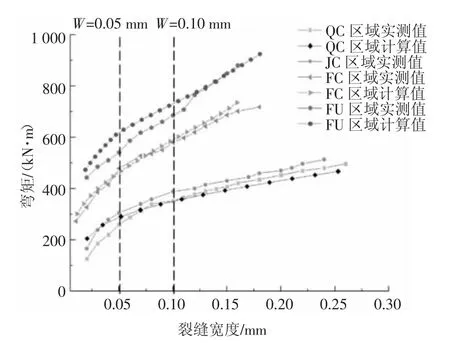
图15 弯矩-最大裂缝宽度曲线图Fig.15 Moment-maximum crack width graph
3.2.4 截面刚度
由2.2节所述布置在各个截面顶、底面的引伸仪测得试验梁在不同弯矩作用下各截面处的曲率(顶底面应变绝对值之和除以梁高)变化如图16所示.由图16可知B/H截面较A/I截面抗裂强度略高,说明界面强度高于母体;由于UHPC的加入,C/G截面较A/I截面抗裂强度和裂后截面刚度均大幅提高;E截面的弯矩-曲率曲线无明显拐点,这与试验中未观察到QU区域出现肉眼可见裂缝相对应.
A/I截面和C/G截面弯矩-曲率曲线的试验值与计算值的对比如图16所示.从图中可看出二者拟合良好.通过3.1节所述数值分析可以得到背景桥例中这两种截面类型在不同弯矩下截面切线刚度与其初始切线刚度的比值(定义为刚度残余系数,其简化计算方法为弯矩-曲率曲线上相邻两点的差商与初始相邻两点差商之比)的变化,图17中纵坐标为截面的刚度残余系数,横坐标为M/Mcr的无量纲系数,其中M为截面弯矩,Mcr为C/G截面的初裂弯矩.A/I截面对应于NC连续梁,开裂后截面刚度迅速下降;而C/G截面对应于负弯矩区湿接缝构造中引入UHPC的混凝土连续梁,其截面第一个明显拐点为NC开裂,第二个明显拐点为UHPC开裂,UHPC开裂后刚度显著下降,后期平稳阶段的截面刚度仅由受压区NC及钢筋提供.UHPC的引入大大提高了截面的裂后刚度,减缓了截面刚度折减的速率,这使得连续梁裂后截面刚度折减而导致的跨中区域内力增大现象显著减弱.经计算,当M=(1~2.5)Mcr时,C/G截面的刚度残余系数约为A/I截面的1.5~5倍.
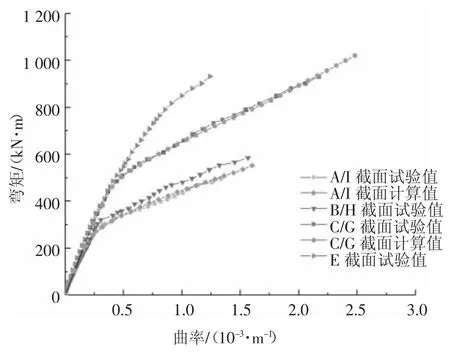
图16 截面弯矩-曲率试验曲线及与计算曲线对比Fig.16 Section bending moment-curvature test curve and comparison with calculation curve
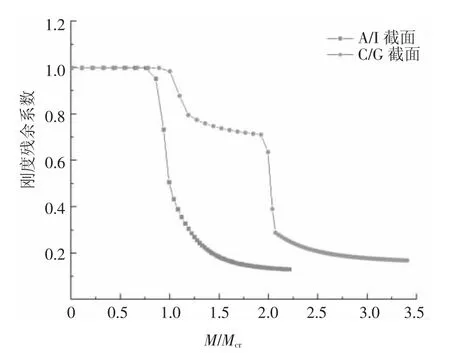
图17 截面刚度残余系数随截面弯矩的变化曲线Fig.17 Variation curve of section stiffness residual coefficient with section bending moment
为得到背景桥例裂后的内力和跨中位移重分布的情况,需要先确定该状态下中支座两侧的刚度折减范围[29].参考MIDAS/Civil有限元模型受拉顶面应力计算可知,距离中支座0.18倍的单跨长度以外时,其受拉顶缘应力小于截面刚度折减点对应的应力,因此取中支座两侧0.18倍单跨长度的范围为截面刚度折减的范围.按照正常使用频遇组合工况下设计应力对应的弯矩,在截面弯矩-刚度残余系数曲线上得到对应的刚度残余系数值,将此截面刚度残余系数和折减范围代入杆系有限单元中得到背景桥例中支座、跨中截面的内力重分布系数和跨中位移的重分布系数,并将其与相同跨径、相同配筋下的传统湿接缝构造(无负弯矩预应力束)混凝土连续梁桥作比较,二者对比如表6所示,由表6可知本文提出的负弯矩区UHPC新型湿接缝构造较传统矩形接缝构造能显著降低连续梁内力和跨中挠度的重分布系数,其重分布系数均大致降为传统接缝构造(无负弯矩预应力束)的30%~50%,此时总挠度小于规范[20]中计算跨径的1/600的限值要求.
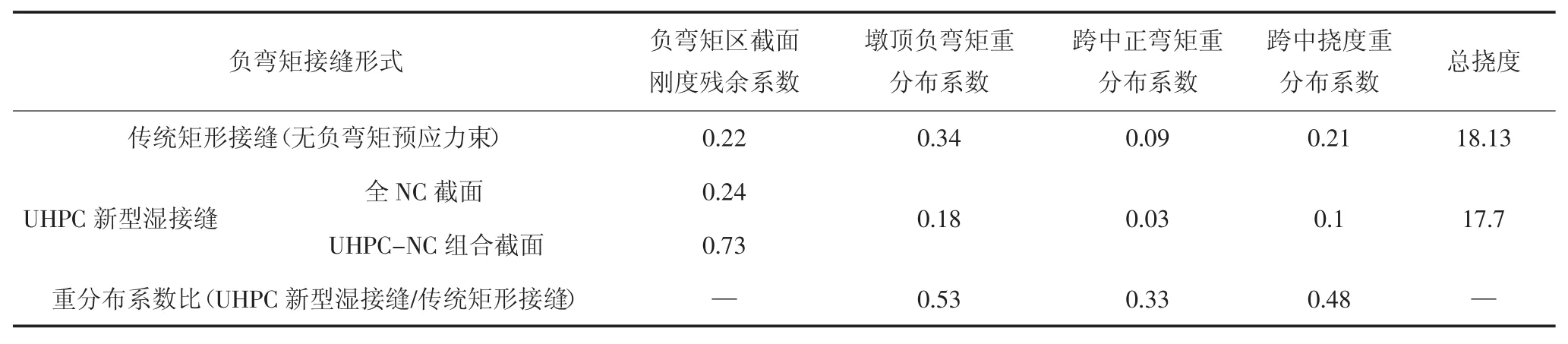
表6 不同接缝构造的连续梁桥截面刚度残余系数及内力、变形重分布对比Tab.6 Comparison of residual stiffness coefficients,internal forces and deformation redistributions of continuous beam bridges with different joint structures
3.2.5 试验结果评价
由于缩尺模型试件与背景桥例满足应力等效,因此可将试验值与实桥的设计值作对比来验证本文提出的负弯矩区UHPC“T形”湿接缝构造是否满足设计要求,结果见表7.由表7可知,在正常使用状态和承载能力极限状态下构件的试验值均大于实桥的设计值,且有一定的安全储备,因此该负弯矩区UHPC“T形”湿接缝构造满足工程设计要求.
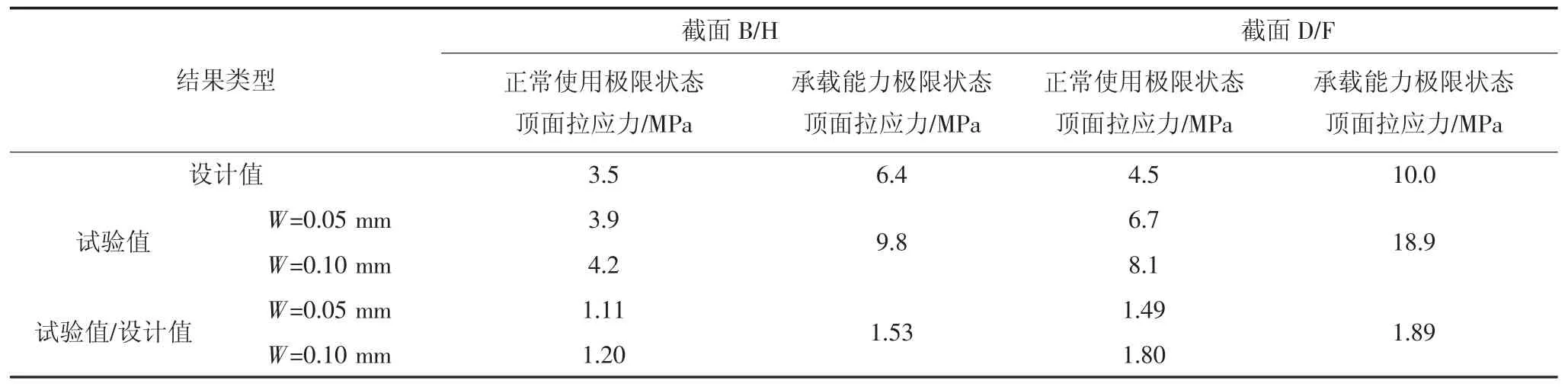
表7 应力结果比较Tab.7 Comparison of stress results
4 参数分析
4.1 UHPC沿纵桥向的长度
现浇UHPC沿纵桥向的外伸段使得全NC截面远离墩顶负弯矩高应力区,提高了结构的抗拉、抗裂性能.表7中正常使用极限状态下交界面(控制截面2)的安全储备较低.因此,为了保证该界面处的抗裂强度具有一定的安全系数,需要重新确定UHPC沿纵桥向的合理长度,其中,安全系数参考文献[30]取1.25.由表7可知,当控制初裂裂缝宽度为0.05 mm和0.10 mm时交界面处顶面的名义开裂应力分别为3.9 MPa和4.2 MPa,为保证实桥中抗裂性能达到1.25的安全系数,MIDAS/Civil软件中实桥交界面处在正常使用极限状态下的顶面允许拉应力在两种情况下分别为3.12 MPa和3.36 MPa.因此当交界面处的初裂裂缝宽度W分别控制为0.05 mm和0.10 mm时,背景桥中UHPC沿纵桥向的合理长度分别为8 m(0.27 l)和6.7 m(0.22 l),为计算跨径.
4.2 UHPC接缝厚度
为研究UHPC厚度对墩顶负弯矩区抗裂性能的影响,保证背景桥例中UHPC沿纵桥向的长度及配筋不变的情况下(UHPC沿纵桥向的长度如4.1节所述,配筋见表2),考虑UHPC的构造要求和梁截面翼缘板高度,取UHPC厚度为60 mm、80 mm、100 mm、120 mm四种情况.不同UHPC厚度下UHPC和NC交界面处正常使用极限状态下的应力设计值和MATLAB的计算值见表8,其中界面处的抗裂强度偏安全地按全NC截面来计算.由表8可知,4种UHPC厚度下,交界面处的抗裂强度均满足设计和工程安全储备的要求.因此考虑经济性,实际工程中可以按照实际情况来取用UHPC的厚度.
4.3 配 筋
为探究钢筋直径对墩顶负弯矩区抗裂性能的影响,取UHPC厚度为60 mm,UHPC沿纵桥向的长度如4.1节所述.讨论UHPC层内钢筋直径为14~28 mm的7种情况.除钢筋直径外,其余布筋参数均与表2中一致,保护层厚度不变.钢筋直径的变化对负弯矩区受拉顶面名义开裂应力的影响见表9(离墩顶0.25 m的UHPC-NC组合截面)和表10(UHPC和NC交界面).
由表9和表10可知,当钢筋直径从14 mm变化到28 mm时,距离墩顶0.25 m的UHPC-NC组合截面(控制截面1)和UHPC与NC交界面(控制截面2)的计算开裂强度均满足设计要求.随着钢筋直径的增大,UHPC-NC组合截面在初裂裂缝宽度为0.05 mm和0.10 mm两种情况下,开裂应力分别提升了24.1%和30.9%,UHPC与NC竖向交界面的开裂应力分别提升了28.9%和37.8%.可见钢筋直径的增大可显著提高负弯矩区截面的抗裂强度.当UHPC内钢筋直径为20 mm时,安全系数均大于1.25,满足抗裂工程安全储备要求.因此全桥负弯矩区统一钢筋直径为20 mm,钢筋的布置形式与表2中一致.

表8 不同UHPC层厚下交界面顶面拉应力值Tab.8 Tensile stress at the top of the interface under different UHPC layer thicknesses
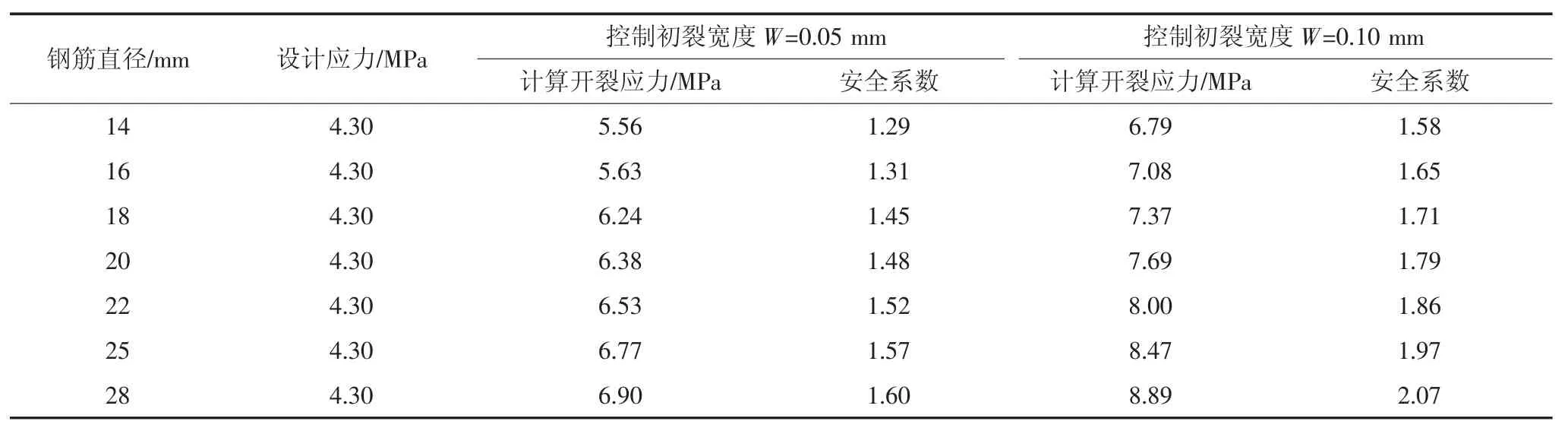
表9 不同钢筋直径对应的UHPC-NC组合截面的名义开裂应力Tab.9 Nominal cracking stress of UHPC-NC composite section corresponding to different steel bar diameters
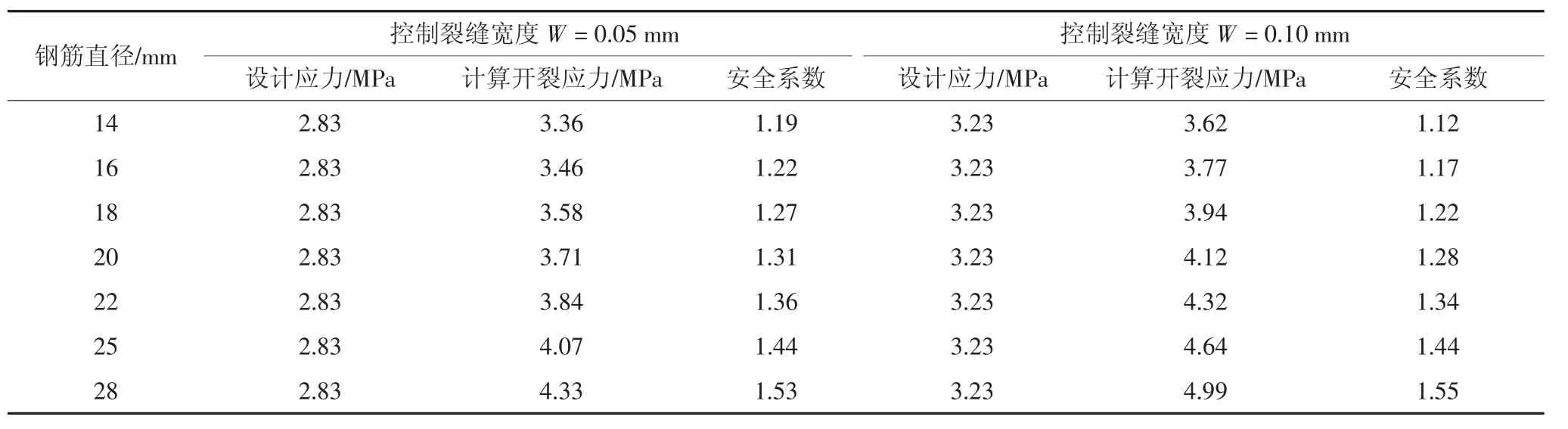
表10 不同钢筋直径对应的UHPC和NC交界面的名义开裂应力Tab.10 Nominal cracking stress at the interface between UHPC and NC for different steel bar diameters
5 结论
本文提出了一种新型的普通混凝土先简支后连续梁的负弯矩区UHPC接缝构造,采用MATLAB数值模拟的方法对其进行配筋试设计,采用1 ∶2的缩尺模型试验对其受力性能进行研究,并对影响负弯矩区湿接缝抗裂性能的因素进行参数分析,得到以下结论:
1)新型UHPC湿接缝构造由于UHPC的引入,取消了负弯矩预应力束的张拉以及钢筋的焊接,消除了传统湿接缝构造因张拉负弯矩预应力束和焊接钢筋带来的施工周期长、质量差的问题.试验证明,新型接缝结构满足抗裂性能和承载能力的工程要求.
2)加载过程中,试验梁的中性轴不断向NC受压底缘移动,最终钢筋基本屈服,UHPC和NC竖向交界面处出现最宽主裂缝.在负弯矩作用下,各截面沿梁高方向的应变均能满足平截面假定,论证了数值模拟条带法计算的前提.UHPC与NC间滑移较小,各部分能较好地协同工作.
3)试验表明UHPC的引入能有效限制NC的裂缝宽度,显著提高NC截面的刚度.与不考虑负弯矩预应力束的传统湿接缝构造相比,本文提出的UHPC新型湿接缝构造能降低混凝土连续梁内力及跨中挠度的重分布系数,均降为传统湿接缝构造的30%~50%.
4)缩尺模型裂缝宽度试验值与计算值拟合良好,表明通过数值模拟抗裂计算来进行负弯矩区的抗裂参数分析是合理的.参数分析表明,UHPC沿纵桥向的长度宜偏安全地取0.27倍单跨跨径.增大UHPC层内受拉主筋直径可提高负弯矩区的抗裂强度,钢筋直径可统一取20 mm,UHPC层的厚度取60 mm即可.
