曲线钢-混凝土组合箱梁桥的爬移行为

2021-04-02王光明季鑫霖季文玉杨顺达

北京交通大学学报 2021年1期

王光明,季鑫霖, 朱力, 季文玉,杨顺达

(北京交通大学土木建筑工程学院，北京 100044)

曲线桥梁的受力特点较直线桥梁复杂，具有典型的弯扭耦合效应，曲线桥梁梁体在竖向荷载的作用下同时承受弯矩和扭矩，在两类作用的相互促进下，梁体的变形较直线桥梁有一定程度的增大[1].曲线钢-混凝土组合梁在实际运营阶段，不仅承受复杂的车辆荷载，而且在车辆荷载和环境温度的耦合作用下，曲线桥梁沿径向外移，导致梁底部与支座接触面的部分滑移无法恢复，这种现象称为曲线桥梁的“爬移”.

近年来，一些学者对曲线桥梁的“爬移”行为及其影响因素进行了相应研究.豆文彬[2]指出曲线桥梁的“爬移”行为会不断积累，只有及时防治曲线梁的爬移病害，才能避免支座脱空、梁体外倾、墩台破坏等二次病害的发生.Wang等[3]针对影响梁体爬移的因素进行分析，指出影响因素主要包括车辆离心力作用、温度荷载作用，混凝土收缩徐变效应等.Tu等[4]对一座两跨混凝土连续箱梁桥开展了数值分析，对温度荷载和边界条件对梁体爬移行为的影响进行分析.刘柱国[5]基于理论分析了温度荷载、预应力、混凝土收缩徐变、汽车荷载等对结构爬移行为的影响，并利用有限元模型对其分析结果进行验证.孙宁[6]指出梁体爬移行为对结构会产生相应的附加内力，从而引起结构自身受力状态的变化，进而产生侧向位移.李根旺[7]对受汽车荷载作用的箱型曲梁桥的动力响应开展了分析，结果表明箱型曲梁桥的动力行为受梁体半径、车辆速度、离心力等影响较大.温度荷载对曲线桥梁的爬移行为有着重要影响.由温度升高导致梁体的横向变形，会使梁体产生径向位移，由于摩擦力的影响，降温后主梁横桥向的侧移变形并不能完全恢复，当该爬移过程循环往复若干次后，爬移位移不断积累.王欣欣[8]指出温度的长期作用会使梁体的侧移不可忽略，应采取措施防止长期爬移行为对曲线桥结构造成的破坏.

钢-混凝土组合桥梁是目前桥梁工程中广泛采用的结构形式，通过剪力连接件将混凝土板和钢梁联结成为统一整体，充分发挥了混凝土抗压性能强、钢材抗拉性能强的优点，显著提高了主梁结构的整体性能和承受能力[9].将钢-混凝土组合梁应用于曲线线形的桥梁结构中可形成曲线钢-混凝土组合梁，其目前广泛应用于市政工程中的高速公路匝道桥.

本文作者重点围绕曲线-钢混凝土组合箱梁桥的“爬移”行为进行研究，充分考虑了各类简化计算方法对梁体爬移行为模拟造成的误差，利用通用有限元软件Abaqus为平台，采用Python语言对梁体进行参数化建模与调参[10]，全过程、全时长地模拟曲线组合箱梁桥的爬移行为.基于有限元模型对曲线组合箱梁桥爬移行为的影响因素展开精细分析，获取不同因素对于曲线组合梁爬移行为的影响特征.基于影响因素分析结果，针对曲线组合箱梁桥的爬移行为特征提出了3种处置措施，利用有限元模型验证了各处置措施的效果.

1 爬移分析的数值模型

1.1 有限元模型

以跨度为50m的两跨连续曲线钢-混组合梁桥为研究对象，其中曲线组合梁的曲率半径为134 m，圆心角为21°，梁体采用单箱双室钢-混凝土组合梁，混凝土顶板厚度为0.2 m，梁体总高1.2 m.梁体两侧及跨中各设置两个板式橡胶支座，支座中心线距离梁体中线1 m.结构的横截面几何尺寸如图1所示.由于梁体纵坡对梁体的切向滑移影响大，对径向“爬移”影响小[2]，梁体不设置纵坡.采用通用有限元软件Abaqus对梁体“爬移”行为开展数值分析，图2为曲线组合箱梁桥的有限元模型.

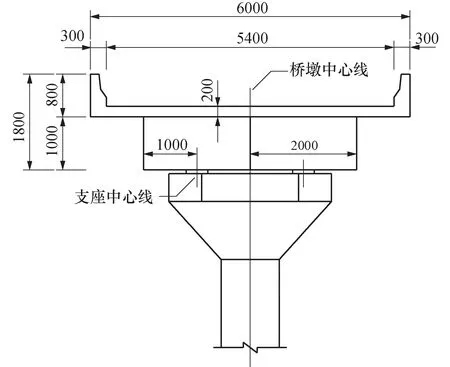
图1 结构的横截面尺寸(单位：mm)Fig.1 Cross-sectional dimensions of the structure(unit: mm)

图2 精细有限元分析模型Fig.2 High-precision finite element analysis model

在曲梁的有限元模型中，混凝土板采用实体单元建立，钢箱采用厚度14 mm的壳单元建立，预应力筋采用桁架单元进行模拟.支座采用Abaqus中的连接器进行定义，不建立实体支座及桥墩，连接器采用Planar类型进行定义，Planar型连接器对支座的平动与转动均能做出约束.规范[11]规定橡胶与钢板之间的摩擦系数为0.2，考虑工程实测值，将支座与梁体间的摩擦系数定义为0.25，梁体在支座上的滑动通过定义连接器的Friction属性实现.

模型中施加的荷载有离心力、温度荷载及预应力.离心力依据规范[11]设置，设计车速为80 km/h，离心力系数为0.376，计算得离心力大小为8.84 kN/m，作用点位于桥面处，作用方向指向梁体外侧.

为了考虑Abaqus数值模型中温度荷载的影响，采用热-应力研究方法对已建立的有限元模型施加温度荷载.热-应力研究方法由温度荷载施加与结构计算分析两个重要阶段构成[12].

为准确模拟有限元模型的温度场及热量传递过程，需要在有限元模型中为混凝土定义换热系数ht、热传导率kc、辐射发射率ec、辐射吸收率ac，为钢材定义换热系数hb、热传导率ks、辐射发射率es、辐射吸收率as.将模型单元属性定义为传热单元.

有限元模型中，表面换热系数用于模拟对流换热作用，通过调整梁体表面热流密度模拟太阳辐射作用，利用热传导率实现结构热传导，通过定义辐射发射率和吸收率实现梁体的对外热辐射作用.数值分析初始环境温度Tamb及梁体初始热沉温度Tf均设置为20 ℃，通过开展热稳态分析，获取模型不同单元节点的温度值，并整理汇总所得温度荷载数据，形成在结构计算分析阶段所需的温度场文件.

在对结构进行受力分析时，需要将有限元模型单元属性重新定义为三维应力分析单元，之后将在温度荷载施加阶段得到的温度场以预定义场的形式输入模型.对于模型所使用的各种材料的温度属性，采用经验值和相关研究的推荐值[13]，表1给出了数值模型中混凝土和钢材的材性参数.

为对结构进行精确热分析，需要对有限元模型的热力学边界条件进行准确定义.为此，在求解温度场的热分析模型中，定义4种热力学边界条件如图3所示，分别为热传导作用、梁体向外热辐射作用、对流换热作用、日辐射作用.

表1 材性参数

图3 梁体热力学边界条件示意图Fig.3 Schematic diagram of thermodynamic boundary conditions of the beam

温度荷载随时间的变化可以通过设置温度荷载的幅值进行模拟，选取2019年7月1日北京市海淀区的气温24 h变化曲线对组合梁受到的环境温度荷载进行模拟，气温变化曲线如图4所示，气温变化数据由清华大学气象站实时监测并记录.

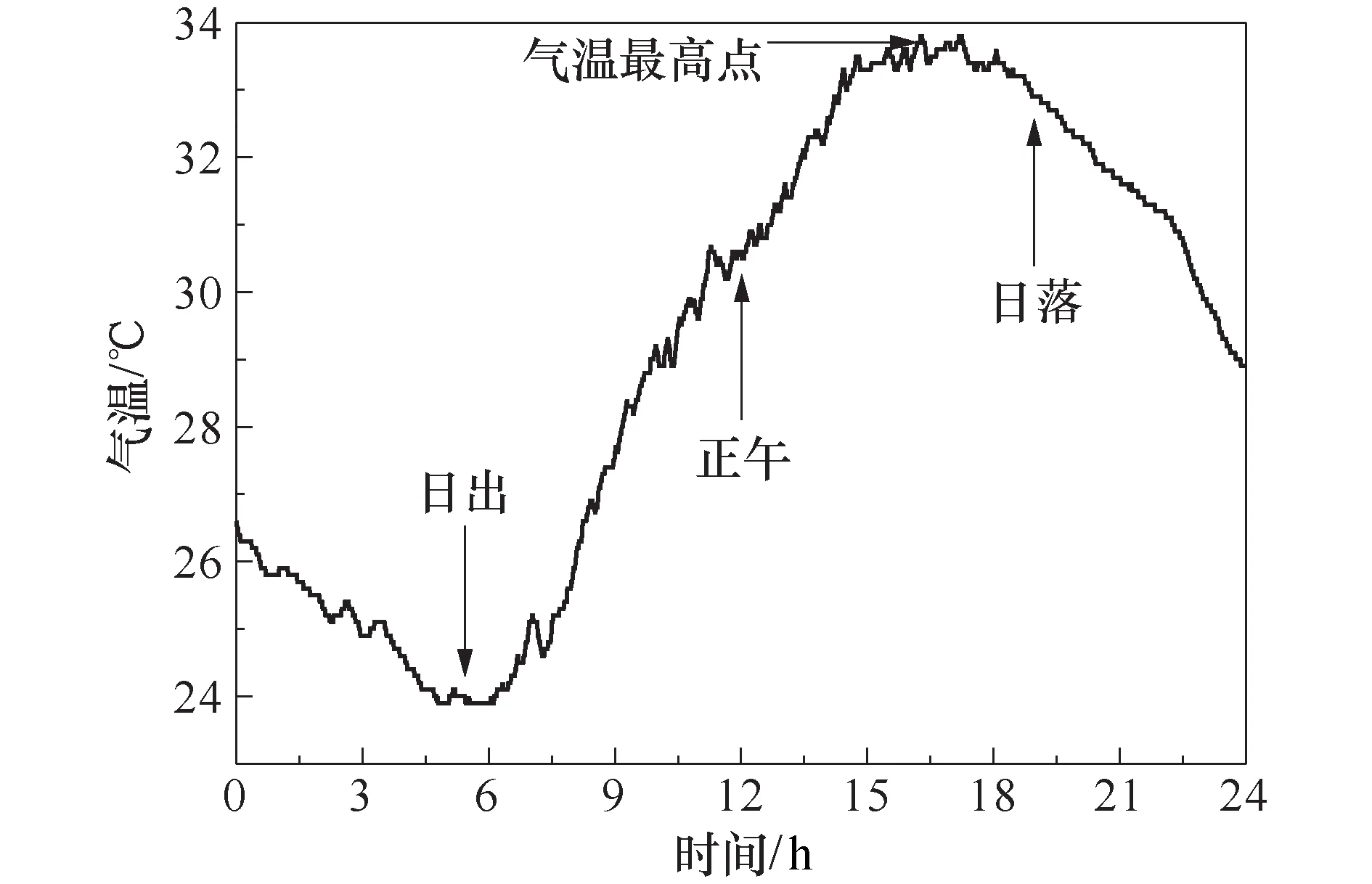
图4 气温模拟曲线图Fig.4 Temperature simulation curve

由于桥梁主要承受太阳光线直接照射，热分析模型仅考虑太阳直接辐射作用，而忽略阳光天空散射和地面反射对梁体所受荷载的影响.太阳直接辐射强度模拟曲线采用Duffie模型[14]进行验证，结果表明，Duffie模型对天气晴朗的北京地区地面的太阳辐射强度有较为准确的预测.综合考虑太阳的高度角、阳光入射角和不同材料的辐射吸收率，可将太阳直接辐射强度转换为钢梁和混凝土板所接受的热流密度，计算得到太阳直接辐射强度和梁体表面热流密度随时间的变化曲线如图5所示.

图5 太阳辐射模型Fig.5 Solar radiation model

热分析模型得到的梁体温度场数据较为复杂，但梁体沿桥跨方向的温度变化不明显，沿梁体横向的温度变化较为显著.为简化分析，便于研究组合梁各部分的温度场分布，在梁端混凝土板顶面(腹板上方与横向跨中)与钢箱底面(腹板下方与横向跨中)各选取两个节点进行监控，测温点位置如图6所示，测温点处温度24 h变化曲线如图7所示.

图6 温度测点示意图Fig.6 Schematic diagram of temperature measuring points

图7 组合梁温度变化对比图Fig.7 Composite beam temperature variation comparison

由图7可知，混凝土板顶面温度明显高于钢箱底面温度，而钢箱底面温度与环境温度相差不大.在Abaqus模型中，为使梁体温度场实时变化，需要将热分析模拟的计算结果实时导入到热应力计算模型中，进行全结构的受力分析.

1.1.2 预应力荷载

数值分析中采用降温法模拟预应力作用.在有限元模型中，采用桁架单元对预应力筋进行模拟，模型中预应力束以曲线布筋方式布置于梁体负弯矩区段的腹板上方，形状与梁体走向一致，每束预应力筋张拉控制应力为1 395 MPa.在有限元模型所处的三维空间中，梁体平面位于O-xz平面内，梁体高度方向为y方向，未施加预应力和施加预应力作用后梁体x方向的Mises应力云图如图8所示.由于模型中预应力作用下的混凝土板受压，压应力可以抵消一部分曲线组合梁负弯矩区混凝土板的拉应力，预应力荷载大大减小了梁体开裂的可能性.

图8 施加预应力前后Mises等效应力对比图Fig.8 Equivalent stress Mises comparison before and after prestressed

梁体有限元模型通过Abaqus自带的Python编程接口实现了参数化建模与求解.Python编程语言在参数化建模分析中,具有独特的优势，通过用少量的代码即可以实现某一建模操作的重复运行，并且可以自主控制分析过程，便于进行参数化的软件操作.在将建模过程分解为多个分析模块时，各模块互不影响，独立可移植，使得程序调试方便快捷，调试脚本周期得到缩短[10].其中，Python语言包特定的模块包括Material和Section模块，Constraint和Interaction模块，Boundary condition和Load模块等，可通过这些模块中规定的函数来实现模型的几何参数、材料属性、边界条件以及荷载的定义.

1.2 “爬移”模拟流程

采用Python语言对Abaqus模型进行二次开发，并分析曲线钢-混凝土组合梁爬移效应的流程图如图9所示，对应的具体操作流程为：

1)依据Abaqus的建模流程编写曲线组合梁模型的Python程序，其中分析步时长定为1 d，并将计算结果写入输出文件.

2)用Python程序提取步骤1)输出文件中各个支座的位移，以确定当前分析步的支座位置，并对模型支座位置参数进行覆盖，其他参数保持不变，最后将该分析步计算结果写入输出文件.

3) 重复步骤2)，迭代计算至循环次数达到预定计算天数为止.

通过如此迭代循环操作，不仅能够计算出每个时间增量步下支座位移的大小，而且能通过后处理模块得到支座位移的整体变化趋势.

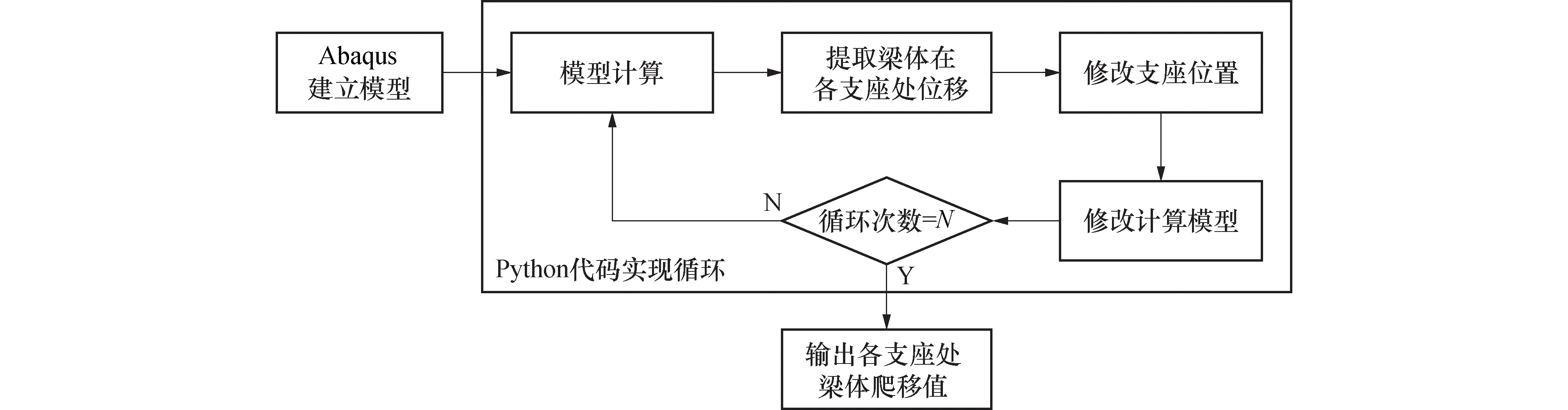
图9 爬移行为数值分析的流程图Fig.9 Flow chart of numerical analysis for lateral deviation behavior

1.3 数值结果分析

1.3.1 横向爬移

在模拟曲线钢-混凝土组合连续梁桥的爬移行为时，将模型中各分析步总时长设置为1 d(即86 400 s)，循环计算365次.依据计算结果输出各个支座的时变位移，并以30 d为时间增量提取各支座相应的位移值，支座位置及编号如图10所示，绘制各支座位移随时间变化曲线如图11所示.

图10 梁体支座布置示意图Fig.10 Layout diagram of beam bearings

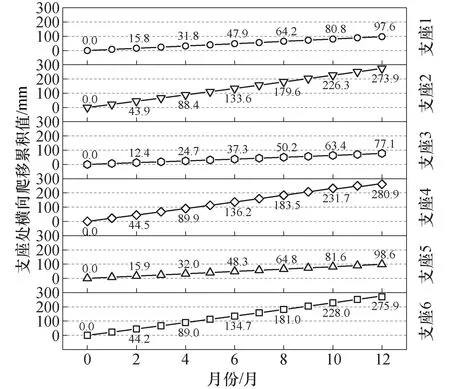
图11 第1 a内支点的横向爬移积累Fig.11 Lateral deviation accumulation on supporting points in the first year

由图10曲线的线形走向可知，6个支座的横向爬移位移均与时间成线性关系.其中，布置在组合梁内侧的1号、3号、5号三个支座由于靠近约束点而位移增长缓慢，但布置在组合梁外侧的2号、4号、6号三个支座由于远离约束点而位移增长迅速.

在一年的分析时间里(365次循环)，各支座的横向总位移在90～290 mm之间.4号支座是跨中外侧支座，由于支座约束，梁体在4号位置处只能产生径向变形，而其横向总位移达到了最大的280.9 mm；2号和6号支座虽然位于组合梁外侧，但也位于梁端，导致其支座位移被分解为径向和切向两部分，故而其横向位移相较4号支座较小.整体看来，分析时间越长，支座残余位移积累越多，爬移行为越显著.

一年内各特征天数的单日支座位移量如表2所示.从中可知，第360 d支座的单日横向位移最大，内侧支座的单日爬移位移介于0.2～0.3 mm之间，明显小于外侧支座的0.72～0.83 mm之间.同时，单日支座位移随时间不断增大，但增长幅度特别小，变化并不明显.综上所述，曲线梁的横向爬移位移随着时间不断增大，一年内，爬移距离最大值接近300 mm，梁体爬移趋势如图12所示.

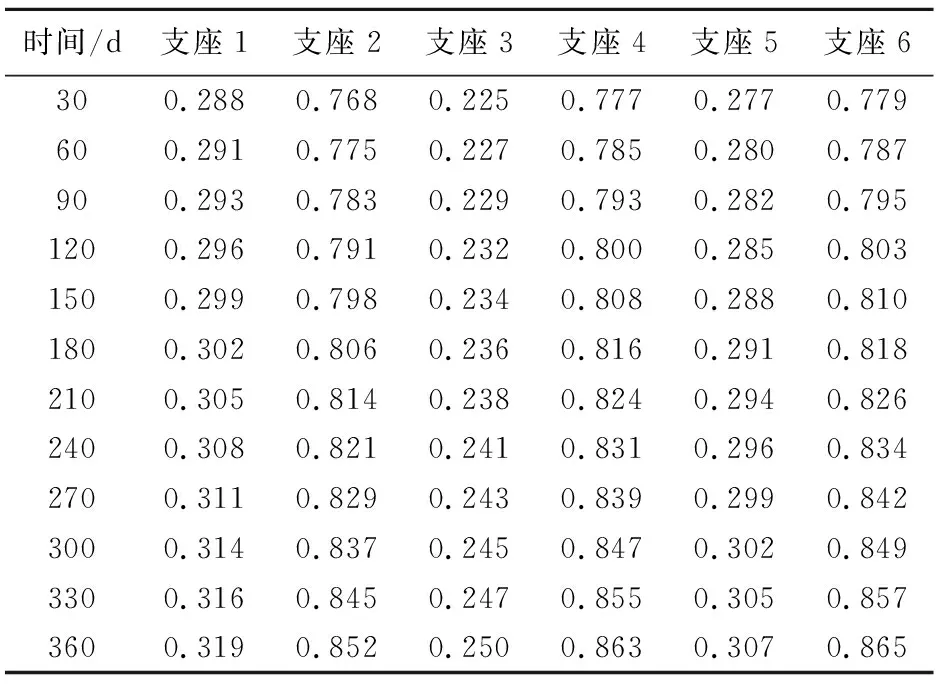
表2 第1年内某时刻的横向爬移

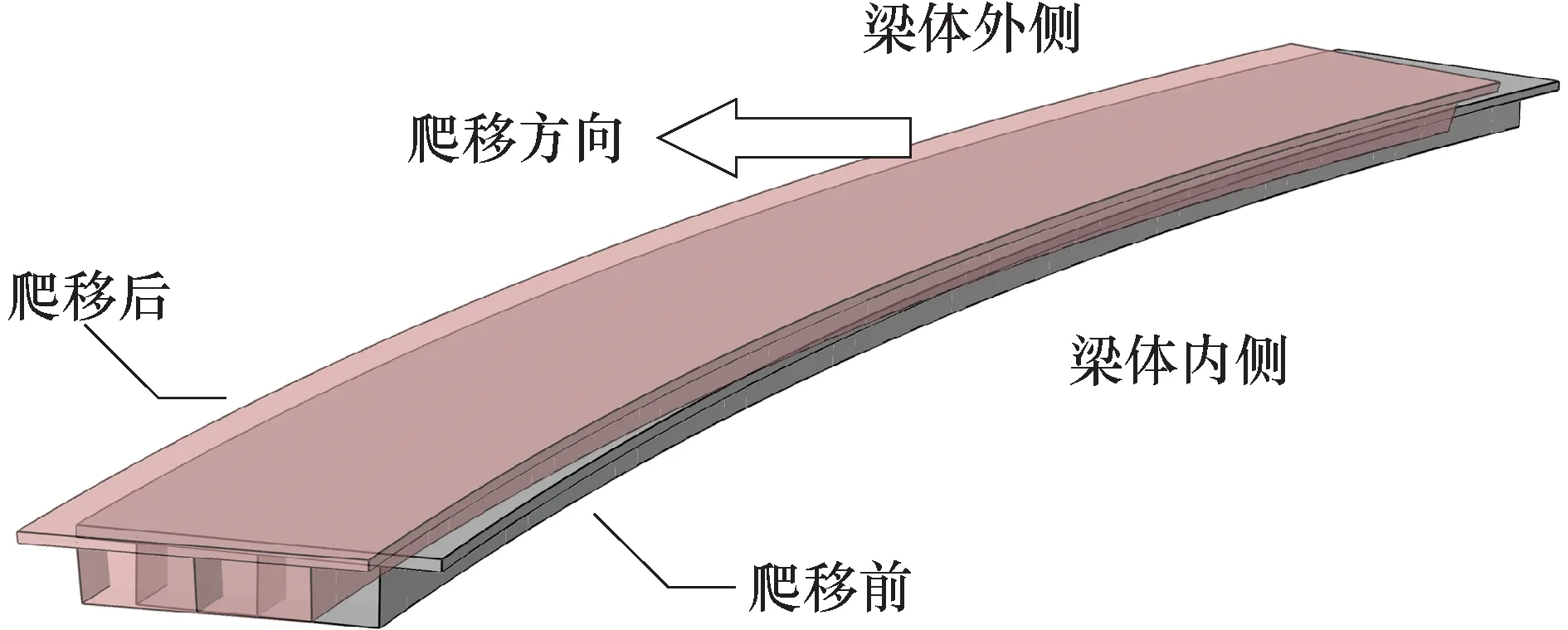
图12 梁体位置状态变化示意图Fig.12 Schematic diagram of position status change of beam

1.3.2 支座受力

与直线桥梁不同，曲线桥梁由于独特的结构，重心向外侧偏离支座连线，其特有的扭转变形与畸变的受力特点，导致曲线梁的内外侧支座有明显的反力差.由于支座的横向位移，曲线梁的重心不断地向外移动，这使得内外侧支座的反力差进一步增大，内侧支座甚至会出现受拉的现象，这对桥梁的安全运营有着极为不利的影响，需要重点分析.

曲线梁模型在梁体爬移前后支反力的变化如图13所示.由图13可知，在未发生爬移时，曲线桥支座受力不均，外侧支座与跨中支座的支反力较大，最大支反力出现在4号支座，支反力大小为604 kN；最小支反力出现在1号和5号支座，大小均为159 kN.发生爬移后，各支座支反力分布趋势基本一致，外侧支座与跨中支座的支反力仍较大，最大支反力出现在4号支座，支反力大小为677 kN；最小支反力出现在1号和5号支座，大小为121 kN和120 kN.

图13 梁体支反力统计Fig.13 Statistics on the reaction force for beam

通过分析图13可知，由于梁体始终处于受力平衡状态，在梁体发生爬移后，梁体内侧三个支座的支反力均减小，其中3号支座支反力减小的幅度更大；而外侧支座的支反力均增大，其中4号支座的支反力增长幅度更大，曲梁爬移行为对支反力的影响显著.

2 爬移因素分析

有限元模型通过参数化建模方式建立，并可通过调整Python语句模拟曲线桥模型在各种因素下的梁体变形.通过改变程序中的参数来实现温度荷载、曲率半径、离心力等单个因素影响下曲线桥的变形.

2.1 温度影响

以是否施加温度荷载为变量，提取出与之对应的第1日梁体爬移量、挠度、应力等特征参数[15]，绘制曲线如图14所示.

由图14可对梁体位移及应力变化情况做出分析.对于梁体位移变化，曲线组合梁1/4跨处的挠度最大，温度荷载对其几乎没有影响；施加温度荷载后，梁体径向位移减小，甚至向内侧移动，但变化不明显；是否施加温度荷载对梁体切向位移影响最为显著，变化最大点位于梁端；对于梁体应力变化，施加温度荷载后，1/4跨处梁底拉应力略有增大，跨中负弯矩区的梁底压应力略有减小，梁顶混凝土板的应力几乎不受温度荷载的影响.

2.2 离心力影响

采取与分析温度荷载影响一致的分析方法，以是否施加离心力作用为变量[16]，提取第10 d两种工况下的支座位移，如图15所示.

图15 离心力对支座径向爬移的影响Fig.15 Influence of centrifugal load on radial deviation of beam bearing

由图15可知，无论是否存在离心力作用，梁体均向外侧爬移；施加离心力后，梁体爬移量略微增大，最大差值为0.03 mm，出现在梁体跨中位置.总体看来，离心力相较其他因素对梁体爬移行为影响较小.

2.3 曲率半径影响

基于已建成的曲线梁模型，采用控制变量法，保证除曲率半径外的其他参数设置不变，以分析去曲率半径对梁体爬移的影响.模型曲率半径变化拟定为95，134，200，300，500 m[17]，用Python程序提取出五种曲率半径下的支座位移如图16所示.

图16 曲率半径对梁体切向爬移的影响Fig.16 Influence of curvature radius on beam tangential deviation

由图16可知，当曲率半径较小时，支座的切向位移差别较为明显，但当曲率半径较大时，相较于2 300 mm的计算跨径，该曲线梁可视为直线梁，故而支座切向位移趋于相等.曲率半径对梁体径向爬移的影响见图17.

图17 曲率半径对梁体径向爬移的影响Fig.17 Influence of curvature radius on beam radial deviation

由图17可知，3号和4号支座的径向位移都随着梁体曲率半径的增大而增大，其他支座的径向位移随着曲率半径的增大而减小，最终趋于稳定.2号和6号支座的位移方向随着曲率半径的增大而发生了改变，从而使得梁体滑移减小，这从另一个方面印证了曲梁向直梁的转化趋势；依据图17对不同位置处支座位移情况进行分析可知，曲率半径对梁端支座的位移影响更大，而对跨中支座的影响较小，各支座位移差随着曲率半径的增大而减小.综合上述分析可知，随着曲率半径的增大，曲线梁桥的爬移行为所受影响越小.

3 曲梁防爬移措施

基于对曲梁爬移行为影响因素的参数分析，结合曲线桥梁的结构与受力特点，充分考虑施工条件的限制，提出设置侧向限位装置、设置支座预偏心、增加两侧支座间距等3种防治措施.

3.1 设置侧向限位装置

针对曲线梁的爬移现象，可以在桥墩设置侧向弹性限位装置[18]，如图18所示.在梁体发生变形与爬移时，以水平支反力的形式对梁体进行约束，从而限制其横向位移的发生.

图18 侧向限位装置Fig.18 Lateral restrainer

基于侧向限位装置的原理，分别建立设置与不设置支座限位装置的有限元模型.侧向限位装置采用连接器进行模拟.连接线一端连接至梁体侧面，另一端选择“连接至地面”，连接器平动属性采用“笛卡尔”类型，不赋予连接器的转动属性[8].侧向限位装置的轴向刚度设置为30 kN/mm.计算得到的各支座径向位移如图19所示.由计算结果可知，增设限位装置后，外侧支座径向位移由原来的0.8 mm左右减小到了不到0.2 mm，内侧支座径向位移减小了约0.1 mm，这说明该侧向限位装置有效地减小了梁体的爬移现象.

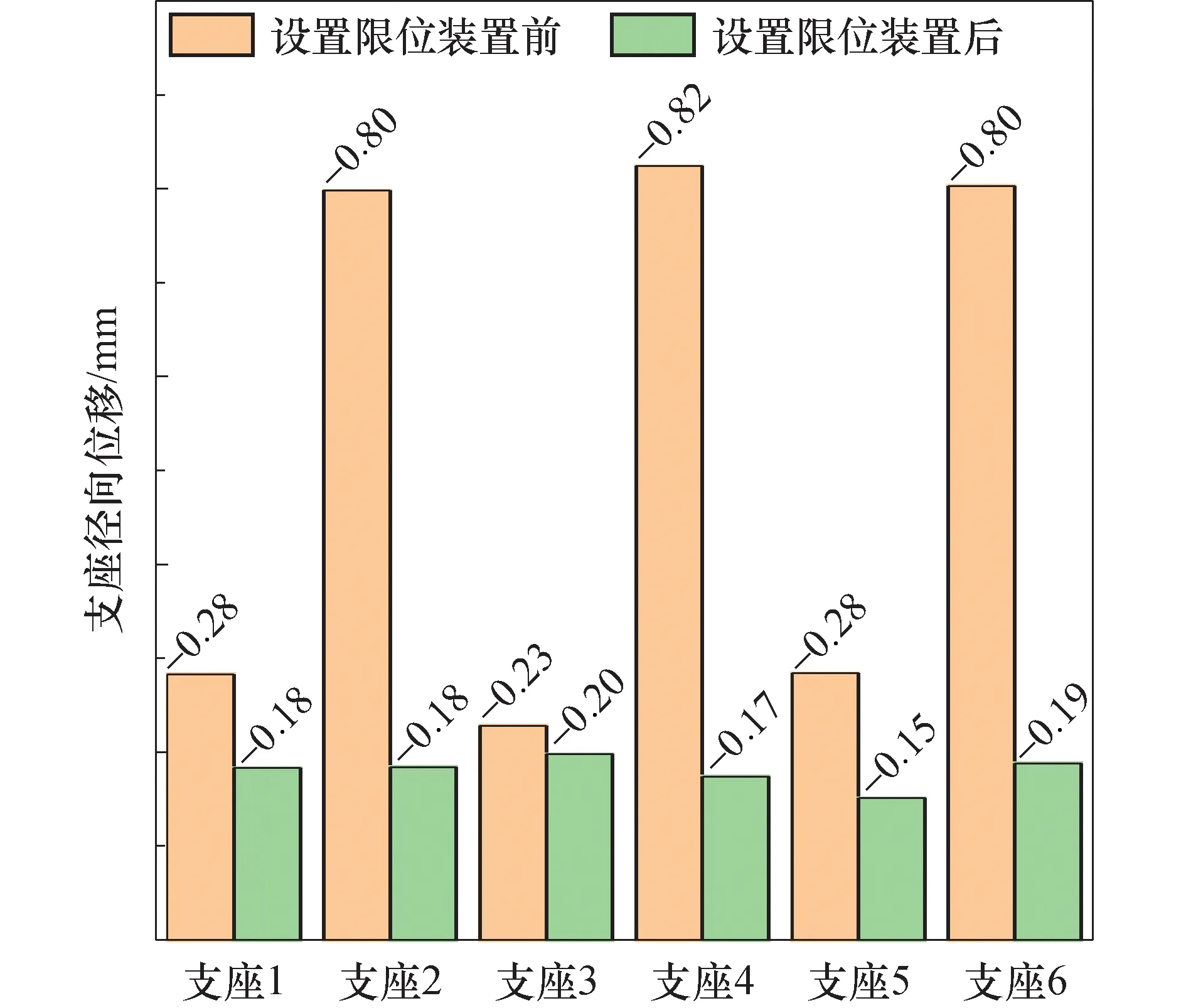
图19 设置限位装置前后支座径向位移对比(单位：mm)Fig.19 Radial deviation of beam bearing before and after setting restrainer(unit: mm)

3.2 设置支座预偏心

连续曲线梁广泛应用的城市公路立交桥和匝道桥中，为了节省桥下空间，中间桥墩通常会设计为独柱墩的形式，跨中支座采用单点铰支座.对于该设计方案，可以在桥梁建设时施加支座预偏心来减小梁体的爬移行为.在有限元模型中,设计50、100、150、200 mm等5个支座偏心距用以研究支座预偏心对爬移行为的影响[17]，计算结果如图20所示.

图20 设置支座预偏心后的支座力学行为Fig. 20 Mechanical behaviors of beam bearing with pre-eccentricity

由图20(a)可知，跨中铰支座偏心距对梁端支座的径向爬移位移几乎没有影响，但跨中铰支座的径向位移随偏心距的增大而不断减小.由图20(b)可知，跨中铰支座的支反力受偏心距的影响不大，外侧端支座支反力随偏心距的增大而增大，内侧端支座支反力随偏心距的增大而减小，但曲线斜率较小，变化较为缓慢.上述规律产生的原因是偏心距的增加使得跨中铰支座对梁体提供的扭矩增大，降低了端支座的内外支座应力差，优化了梁体的受力状态，从而起到抑制梁体爬移的作用.

3.3 合理增加两侧支座之间的距离

由曲线梁的受力特性可知，其支座支反力的大小与外荷载产生的扭矩有关，而支座间距的增大可以在一定程度上增大支反力对梁体产生的扭矩[19]，因此，在同样的外荷载作用下，可以通过适当增加组合梁钢箱整体宽度的方式增加支座间距,以达到有效地减小各支座的支反力大小，改善曲梁受力状态的目的.支座布置示意图如图21所示.

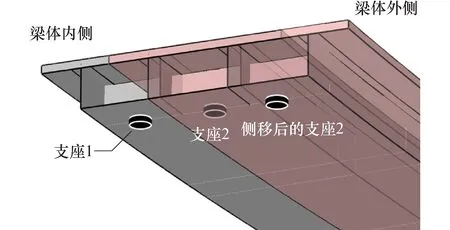
图21 增大支座间距示意图Fig.21 Schematic diagram of widening spacing between bearings

分别计算初始支座间距为2 m、增大后支座间距为3 m的情况下各支座的反力值，计算结果如表3所示.从表中数据可以看出，随支座间距离的变化，支反力呈现重分布现象.数据显示，1号、3号、5号三个内侧支座其支反力呈现增大趋势，2号、4号、6号三个外侧支座则相反，两侧差值减小，可能呈现出跨中外侧支座支反力低于内侧支反力的现象.这说明支座间距增大后主梁的中心靠近内侧支座连线，该方法在一定程度上增大了曲梁爬移的极限距离，可有效降低曲梁爬移造成的病害.