基于概率统计理论的铁路桥梁损伤识别方法

陈一凡，孙利民,2

（1.同济大学土木工程学院桥梁系，上海 200092；2.同济大学土木工程防灾国家重点实验室，上海 200092）

1 引言

基于概率统计的方法已被广泛应用于检测结构损伤。由概率密度函数拟合响应分布，然后比较各种损伤状况下分布函数的变化，可以评估结构状态。然后，建立损伤因子的置信区间来评估损伤程度，可以显著改善运营养护决策。其他的研究利用统计理论来分析监测数据，并从分析结果中提取损伤指标。一些研究直接从监测数据中获取统计指标作为损伤指标，例如峰、均值、均方根、方差、标准差以及偏度等，但是，它们的性能会受到环境因素的影响。因此，一些研究通过消除温度效应和交通效应等的影响，从处理后的监测数据中提取统计损伤指标。此外，直接使用原始数据来重构所需数据也是一个很好地解决方案，可以从新的数据集中提取统计指标，以估计损伤程度。

2 基本理论

本研究进一步利用铁路列车过桥过程中的梁端倾角时程数据进行桥梁结构损伤识别，首先进行车轨桥耦合振动计算以获取桥梁响应。对于车轨桥振动系统，可将车辆视为一个子系统，轨道及桥梁视为另一个子系统，车辆子系统的运动微分方程可表示为：

轨道及桥梁子系统的运动微分方程可表示为：

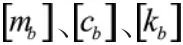
借助于同济大学李奇教授团队编制的控制台程序VBC2.0，利用龙格库塔法可以数值求解桥梁梁端处的倾角时程α(t)，通过改变输入的车速得到不同的时程序列 α(t)：

即不同倾角时程序列间的差异仅由输入车速不同引起。随后提取每段时程序列中的最值指标作为它们的特征θ，即各倾角时程绝对值最大的n个值的平均值：

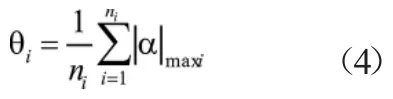
式中n为第i个车速下桥梁发生自由衰减振动之前时程数据点个数的1/300，可通过以下简单计算得到：

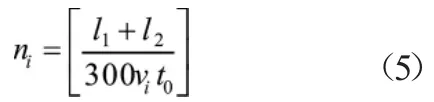
式中l为轨道总长，l为列车总长，v为第i个列车行驶速度，t为时间步长。

此时建立了车速与时程特征的映射关系：

不同铁路列车经过同一点的速度值可以视为在某个区间内随机出现，因此本研究假设经过桥上某点的车速服从某种特定的分布p(v)，根据上述速度—倾角的映射关系可以得到倾角的概率密度：

由于倾角θ的分布p与速度、结构状态间的关系难以直接解析表达，故通过蒙特卡洛方法获取结构参数改变后结构倾角的近似概率密度。用随机抽样的方法获得一系列服从某分布的速度序列{v}，再利用上述映射关系可得倾角的随机序列{θ}。当样本数量足够多时，该倾角的统计结果可近似认为是其概率密度。

最后本研究定义了统计指标：

式中n为核密度估计划分区间数，θ为区间中点对应的倾角指标值，f为拟合曲线上对应于θ的拟合值。

通过对比分析损伤前后的损伤指标差异便可得出结构损伤初步结论。

3 数值模拟

3.1 获取响应数据

本研究主要的研究对象是铁路32m标准跨径简支梁桥。本文使用ANSYS建立该桥的有限元模型，选用beam4单元作为主梁单元，单元数量为32，模型其他参数为：桥长L=32m，弹性模量E=3.5e10Pa，截面惯性矩I=11.2m,密度 ρ=2500kg/m。

轨道模型方面，本文采用单层轨道模型模拟车桥之间的弹性作用，相关参数为：轨道竖向刚度k=0.75e8N/m，粘滞阻尼系数ξ=0.9e5N/(m/s)。

车辆模型方面，本文采用二系悬挂模型模拟列车，并采取一动＋三拖＋一动＋三拖共8节车厢的列车编组方式，以模拟现实情况中客运列车的编组。整个车桥系统的示意图，见图1所示。

图1 车轨桥系统示意图

列车运行速度方面，列车保持匀速行驶，并使计算程序按照{200 km/h，201 km/h，202 km/h，…，300 km/h}共 100个速度进行100次计算。时间步长方面，预设响应输出时间步长为0.001s，时间步长过长会导致计算结果不收敛。

为进行各种工况下的对比分析，本研究设计了以下6种桥梁主梁刚度损伤工况（如表1）。

损伤工况定义 表1

桥梁无损情况下两种车速对应的梁端倾角时程曲线，见图2所示。

图2 倾角时程曲线

此时可以建立列车速度与倾角指标之间的映射关系，利用三次方样条插值法可作出插值曲线，见图3所示。

图3 列车行驶速度v与倾角指标"θ"的映射关系

3.2 随机车速模拟

假设车速遵循某种特定的概率分布，借助于MATLAB产生10000个服从该分布的随机数。结合上文中提到的列车速度与倾角指标之间的映射关系，可以获取桥梁的倾角响应数据。在本项研究中，选择β分布作为列车速度的概率分布。

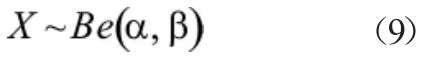
β分布的概率密度函数的形状由参数α和β决定，合理取值可以使随机数覆盖可能的车速范围。本研究选取四组分布参数，其中x服从(0,1)上的均匀分布：

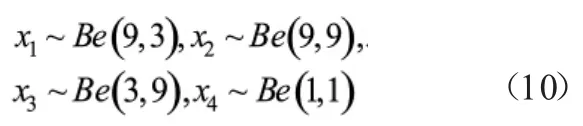
考虑到车速变化范围的广泛性，将β分布与均匀分布的和作为目标分布。

那么车速服从的分布，见图4所示。

图4 车速的目标分布

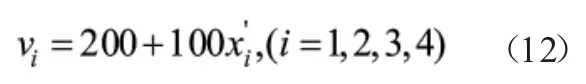
3.3 抽样结果统计分析

得到速度随机抽样数据后，即可根据车速—倾角映射关系获得关于倾角的随机分布数据。为了更好对比各分布之间的差别，本文利用核密度估计对两种情况下的倾角数据进行非参数估计。

其中 x，x，…，x是独立同分布F的不同采样点，f为概率密度函数，K为kernel函数，本文选用高斯核函数，h为带宽，采用MATLAB中的默认值。

拟合曲线如图5所示。

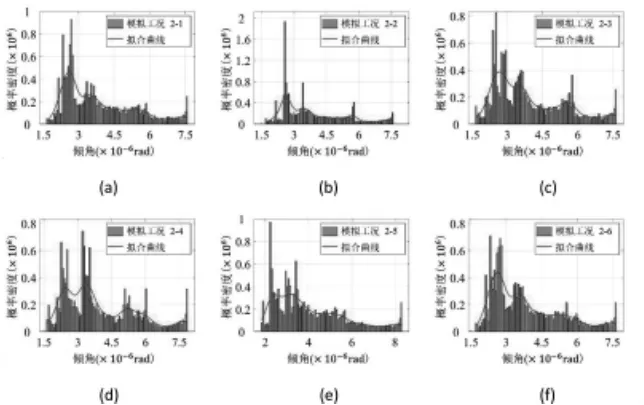
图5 倾角指标θ的分布

图5中图例(a)代表车速服从Beta分布2及桥梁损伤情况为损伤工况1。为量化该拟合的优度，引入指标R-square：

各分布及各工况下的拟合效果如表2所示。

不同状况下的R-square 表2

表2数据显示，各工况下的拟合优度均超过0.9，即拟合效果良好，所以可以通过分析拟合曲线获取感兴趣的信息。图5中的拟合曲线已经直观地展现出损伤前后倾角分布的差异：倾角概率分布密度左侧两个峰值的高低关系发生了置换，同时受损状况下第三个峰值相对于无损状况要高。这些变化均表明了在其他条件不变的情况下桥梁已经发生了损伤。

为了量化损伤前后分布曲线的变化，分别计算各分布及各工况下损伤指标Φ的数值，见表3所示。

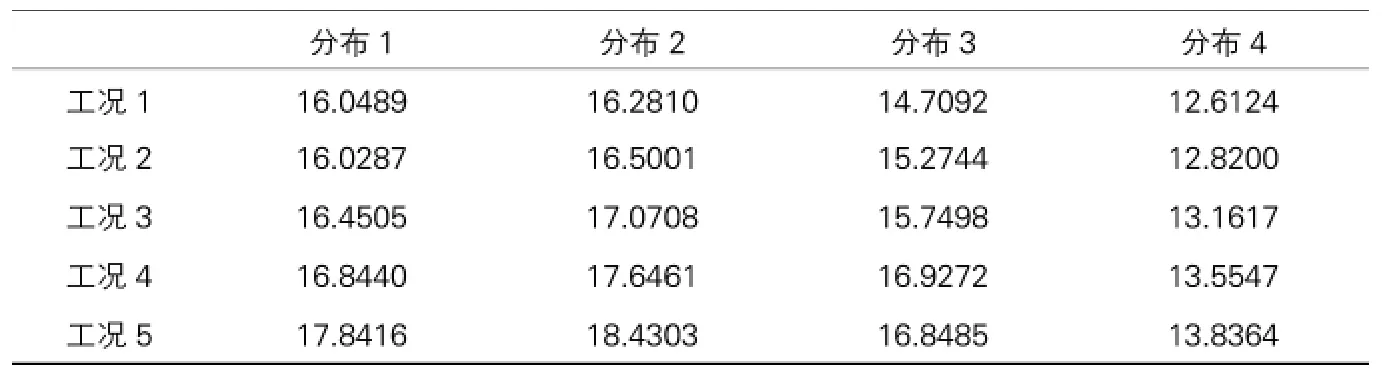
不同状况下的损伤指标值 表3

通过上表的数据可知，无论原始车速服从的是四种分布中的哪一种，损伤指标的数值均随着损伤程度的增大而增大。这是因为随着损伤程度增大，桥梁产生更大倾角的可能性提高，又结合该损伤指标的构成特点，其数值会随之变大。为进一步了解该损伤指标的敏感性，本文还计算了各种损伤工况下相对于原始状态的敏感度，即：

上式中i为第i个工况，Φ为无损情况下损伤指标值。计算结果见表4所示。

损伤指标的敏感性分析 表4

分析表4数据可知，该损伤指标对损伤的敏感程度随损伤加剧不断提高，同时与目标分布有关，在服从分布1的情况下对损伤最不敏感，在服从分布3的情况下对损伤最敏感。同时，该指标对1/4跨处产生损伤的敏感性整体上要大于在跨中产生的损伤。

4 总结与展望

本文提出了一种基于概率统计理论的损伤指标，通过数值算例验证了该指标的有效性，该方法可以根据梁端倾角的统计信息推测桥梁的健康状况，具有实施方便、简单易行、结果直观的优点。通过对统计结果的分析，总结如下：

①桥梁某处发生损伤时，结构自身的刚度减小，在相同行车条件下桥梁的响应会随之变大，且随着损伤程度增大，桥梁结构的响应也将进一步变大；

②本文提出的统计指标是对大量桥梁响应数据的统计描述，可以反映铁路桥梁长期运营所产生海量数据统计特性的改变，并以此为初步判断损伤产生的依据，指导大量中小跨径简支梁桥的运营养护工作；

③本文假设车速服从β分布，通过数值模拟的方式获取结构在无损状况下的统计指标，同时设立了多个损伤工况展开对比研究，但缺乏针对实验或实测数据的验证，需要进一步研究该统计指标在处理真实响应数据时的适用性，使结论更具有实际的参考价值。