国产商用密码算法SM2 及其相关标准介绍

谢宗晓　李达　马春旺

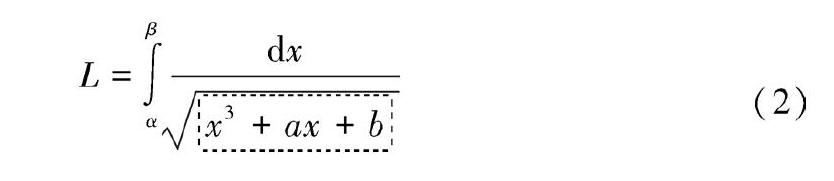
1 概述

公钥密码算法的产生主要是为了解决密钥分发困难的问题1）。1976年，Whitfield Diffie和Martin Hellman提出了公开密钥加密的设计思想，但当时并未能给出实现的算法。之后，有多种算法被提出，但经得住考验得到大面积应用的主要是Ron Rivest、Adi Shamir和Leonard Adleman在1978年提出的RSA算法。直到现在，RSA几乎成了公钥密码领域事实上的标准。关于公钥密码算法的更多基础知识，请参考文献[1]。

RSA算法的安全性，主要是基于大整数质因数分解的困难性，这意味着如果这个整数太小，就很容易受到暴力攻击。所以，RSA算法的密钥，越来越长。NIST2）建议在2010年12月31日前停止使用RSA1024，升级至RSA2048。当然，到目前，也没有明确的证据表明RSA1024已经被破解了，但是从当前计算能力的升级速度推测，RSA1024确实已经不安全了。

密钥长度的不断增加意味着效率在不停地降低，与一味地增加密钥长度相比，寻求更合适的陷门单向函数是解决这个问题更佳途径。Neal Koblitz3）和Victor Miller4）分别独立地在1985年将椭圆曲线引入密码学领域。

2 椭圆曲线密码学

椭圆曲线密码学（Elliptic curve cryptography，ECC）的数学基础远没有RSA算法那么易于理解。首先，椭圆曲线和椭圆是两码事，两者之间联系不大。最常见的椭圆曲线方程，如公式（1）典型的二元三次方程。

但是这个方程的几何表现形式并不是椭圆，或者说，跟椭圆基本没什么关系。其图形如图1中的示例。

之所以被命名为椭圆曲线方程，是因为圆周长有固定的公式，很容易求解，但是椭圆就复杂得多，开始人们想利用微积分计算椭圆的周长，其最终表达式类似于公式（2）。

公式（2）中矩形框标识出来的分母，与公式（1）基本一致，因此形如公式（1）这样的方程，被称为“椭圆曲线”。可见，椭圆曲线密码的基础知识相对RSA而言要抽象得多。因此，GB/T 32918.1—2016《信息安全技术 SM2椭圆曲线公钥密码算法 第1部分：总则》先给出了SM2椭圆曲线公钥密码算法涉及的必要数学基础知识与相关密码技术，在后续的部分中讨论具体的密码机制。

我们不去讨论抽象的阿贝尔群等抽象的概念，直接看图2，椭圆曲线关于X轴是对称的。在椭圆曲线上定义二元运算，即椭圆曲线上的加法。

图2中，曲线上的两个点A和B，连接两点的直线与曲线有且仅有一个交点，该交点关于X轴的对称点，即为A+B。如果A点和B点重合，那么就寻找其切线与曲线的交点，对称点为2A。因此，曲线上的任意点G，我们可以找到，2G，3G，…，nG。G为基点，nG为多倍点。

显然，已知G，求解nG非常简单，但是已知nG，求解n则很困难。这就具备了单向函数的基本特征。已知多倍点与基点，求解倍数的问题称为椭圆曲线离散对数问题，一般椭圆曲线的离散对数问题，求解计算的复杂度是指数级。

椭圆曲线密码学的理论基础就是基于椭圆曲线离散对数的数学难题。GB/T 32918系列标准的引言中指出：与大数分解问题及有限域上离散对数问题相比，椭圆曲线离散对数问题的求解难度要大得多。因此，同等强度的椭圆曲线密码学在安全性和效率上比RSA都有大幅度提升。

3 SM2密码算法标准

国家密码管理局于2010年12月17日5）发布了国产商用密码算法SM2。在算法大类上，SM2属于公钥密码算法（非对称密码算法），就具体实现而言，SM2属于椭圆曲线密码算法。2012年，SM2被采纳为GM/T 0003系列标准，2016年转化为GB/T 32918系列标准。

SM2的发布，主要是为了满足电子认证服务系统等应用需求。表1中给出了SM2密码算法标准的5个部分。

GB/T 32918.1—2016主要介绍了椭圆曲线密码学所用到的必要的数学基础，包括有限域和椭圆曲线等，在第6章中讨论了密钥对的生成，以及公钥的验证，附录C中有椭圆曲线的示例。

GB/T 32918.2—2016描述了用椭圆曲线所实现的数字签名算法和SM2签名算法，关于数字签名的更多资料，请参考文献[2]和[3]。GB/T 32918.2—2016中，第5章介绍了数字签名算法，第6章介绍了数字签名生成算法及其流程，第7章介绍了数字签名验证算法及其流程。

GB/T 32918.3—2016规定了SM2椭圆曲线公钥密码算法的密钥交换协议，并给出了密钥交换与验证示例及其相应的流程。在密钥交换协议中，要用到辅助函数，包括密码杂凑函数、密钥派生函数和随机数发生器。其中密码杂凑函数用到了SM3。

GB/T 32918.4—2016描述了用椭圆曲线所实现的公钥加密算法，SM2加密算法。在签名算法中，签名者用自己私钥加密，验证者用签名者的公钥解密，这就保证了消息发送者是唯一持有密钥的人。在SM2加密算法中，用接收者的公钥加密，接收者用自己的私钥解密，这解决了最基本的密钥传输难题。

GB/T 32918.2—2016和GB/T 32918.4—2016实际给出了SM2最典型的两种用法。

GB/T 32918.5—2016给出了SM2椭圆曲线公钥密码算法的曲线参数。

4 SM2相关标准

密码行业标准化技术委员会还发布了关于SM2的一系列相关标准，具体如表2所示。

GB/T 35276—2017与GM/T 0009—2012，

GB/ T 35275—2017与GM/ T 0010—2012保持了一致。但是，GB/T 20518—2018与GB/T 25056—2018则是根据GM/T 0015—2012或GM/T 0034—2014进行了修订。

GB/T 35276—2017定义了SM2密码算法的使用方法，以及密钥、加密和签名等的数据格式。GB/T 35275—2017则是规定了SM2密码算法的加密签名的消息语法。

GB/T 20518之前有2006年版本，2018年为修订版本，GB/T 25056—2018明确地指出应该优先使用国产密码算法，例如，SM2和SM3等。标准中要求，在证书或CertificateList中的SignatureAlgorithm字段，来标识使用的算法。GB/T 25056—2018之前有2010年版本，该标准则是针对数字认证系统。

5 小结

SM2密码算法，尤其是基于SM2的数字签名技术，在国内金融等行业已经得到广泛的应用，逐步替代了基于RSA算法的数字签名。与大整数质因数分解为数学基础的RSA算法相比，以椭圓曲线离散对数为数学基础的SM2，所需要的密钥长度比较短，也就是说，同样的密钥长度，椭圆曲线密码可以提供更高等级的安全。

（注：本文仅做学术探讨，与作者所在单位观点无关）

参考文献

[1] 谢宗晓，董坤祥，甄杰.公钥基础设施（PKI）的发展过程及其架构[J].中国质量与标准导报， 2020（5）：17-20.

[2] 谢宗晓，甄杰.公钥基础设施（PKI）国家标准解析[J].中国质量与标准导报， 2018（12）：18-21.

[3] 谢宗晓，刘琦.公钥基础设施（PKI）国际标准进展[J].金融电子化，2018（10）：56-58.

[4] 霍炜，郭启全，马原.商用密码应用与安全性评估[M]. 北京：中国工信出版社/电子工业出版社，2020.

[5] 郑昉昱，林璟锵，魏荣，等.密码应用安全技术研究及软件密码模块检测的讨论[J].密码学报， 2020，7（3）：290-310.