基于CFX的内啮合齿轮泵流场瞬态仿真分析

任京芹

(西安工商学院,西安 710020)

0 引言

内啮合齿轮泵是将机械能转化成液压能的一种能量转换装置，为液压系统提供有压力的油液，是液压传动系统中常用的动力元件[1]。内啮合齿轮泵作为一个回转泵，它主要是依靠泵缸与啮合齿轮间所形成的工作容积变化和移动来输送液体或使之增压。它是由两个齿轮、泵体与前后盖组成两个封闭空间，当齿轮转动时，齿轮脱开侧的空间体积由小变大形成真空，将液体吸入；当齿轮啮合侧的空间体积从大变小时，从而将液体挤入管路中去。吸入腔和排出腔主要是靠两个齿轮的啮合线来隔开的，齿轮泵的排出口压力完全取决于泵出处阻力的大小[2]。

泵内流场涉及到流体的扩展吸入、挤压排出等不同状态，流动情况由吸入腔和排出腔的内部流动决定，随着计算机技术和数值模拟技术的不断发展，利用CFX对复杂流场进行分析已经成为普遍应用的工程技术，通过该分析可以有效地仿真出流场在齿轮泵内部的流量、压力等参数的变化情况，可以为齿轮泵设计提供依据。

1 齿轮泵模型

考虑到内啮合齿轮泵的主体是两个齿轮、泵体与前后盖，利用CFX进行流场仿真分析时只需要对齿轮、吸入腔和排出腔进行分析即可，因此，这里对内啮合齿轮泵进行了简化，只保留了齿轮、吸入腔和排出腔以及输入和输出管道，外齿轮的最大内直径7.3 cm。其结构如图1所示。

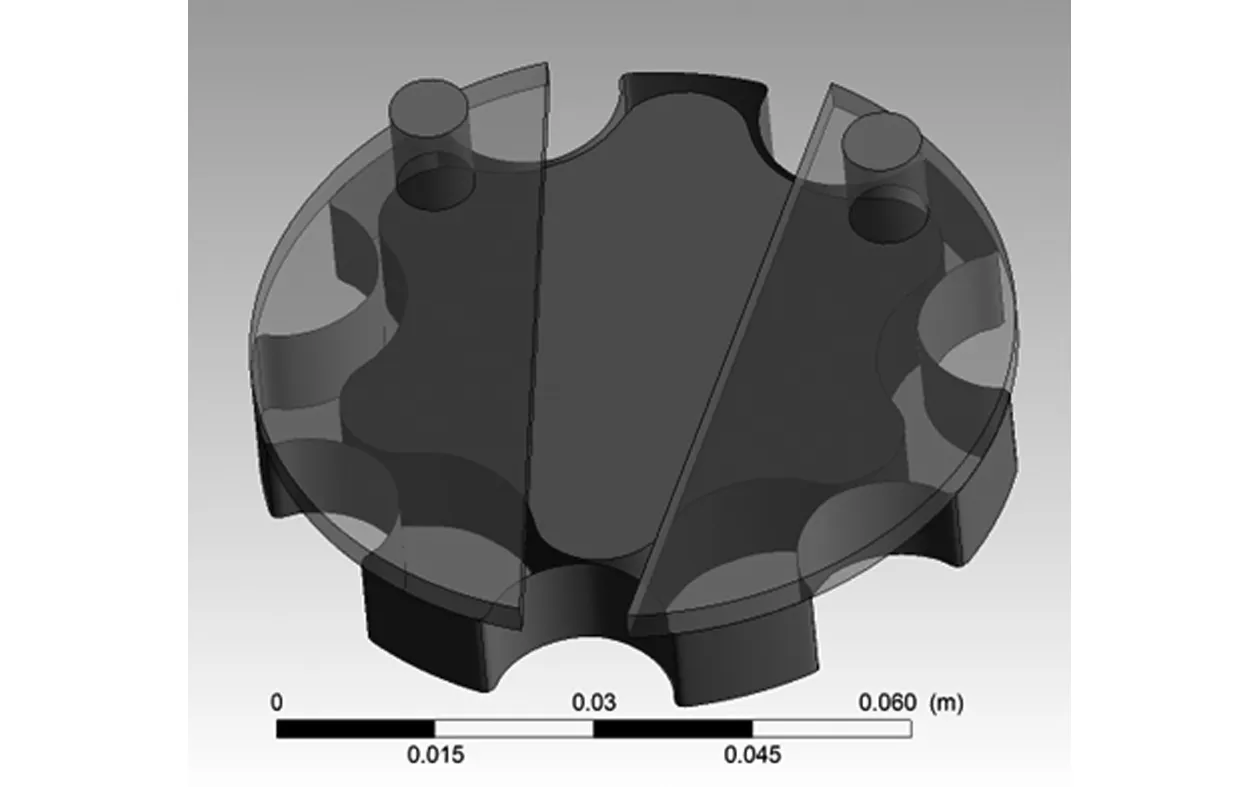
图1 内啮合齿轮泵结构图

2 数学模型

2.1 连续性方程[3]

连续性方程为式(1)

(1)

式中ρ—流体的密度，kg·m-3；

u—流体速度在x方向的速度，m·s-1；

v—流体速度在y方向的速度，m·s-1；

w—流体速度在z方向的速度，m·s-1。

2.2 动量守恒方程(N-S方程)

动量守恒方程为式(2)、(3)、(4)

(2)

(3)

(4)

式中p—流体微元体上的压力，N；

τxx、τyx、τzx—因分子黏性作用而产生的作用在微元体表面上的黏性应力τ的分量，Pa；

Fx、Fy、Fz—微元体上的体积力，N。

2.3 标准k-ε模型

标准k-ε模型中，紊流动能k方程和耗散ε方程[4]分别为式(5)、(6)

(5)

(6)

式中Gk—平均速度梯度引起的湍动能产生项；

C1ε、C2ε—经验常数。

3 数值分析计算

3.1 计算区域

由内啮合齿轮泵的组成可知主要的计算区域为内啮合齿轮泵啮合部分和吸入、排出腔体部分的流体，通过三维建模工具UG完成模型设计后，利用TurboGrid对内外齿轮及腔体进行网格划分，并将划分好的网格存成 .gtm格式供CFX调用，划分网格后模型如图2所示。

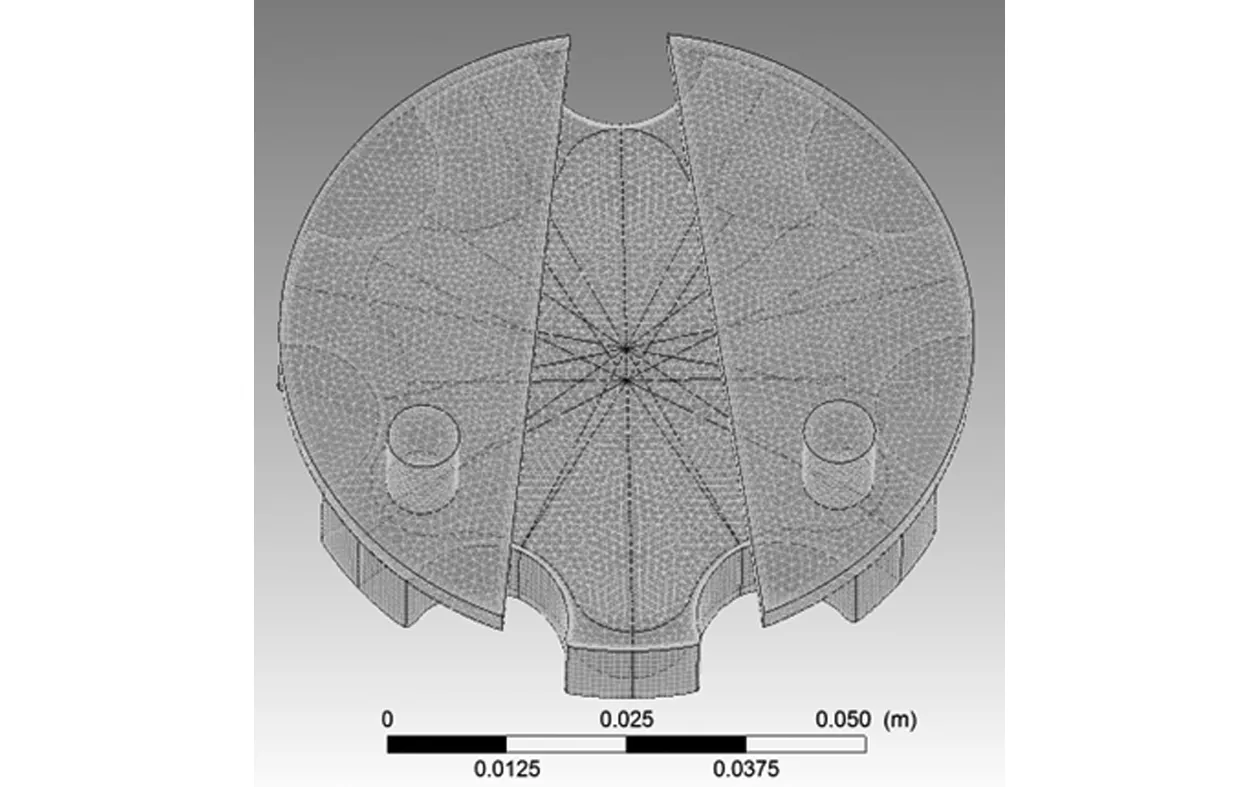
图2 划分网格模型图

3.2 运动分析

考虑到流场瞬态计算的计算量较大，这里取每个齿轮的单步运动作为研究对象，内齿轮齿数为6，外齿轮齿数为7，为了保持齿轮之间的啮合，内齿轮转速设定为7 r·s-1，外齿轮转速设定为6 r·s-1，因此内外齿轮的单步运动时间均为1/42 s，将单步运动时间的1/30作为瞬态步长，取3个单步运动作为仿真的时间总长进行仿真分析。

3.3 边界条件设置及计算模型选择

内啮合齿轮泵的流场域可分为齿轮间的流动域和两个腔体的静止域，选择标准k-ε模型作为计算模型，将内外齿轮分别作为绕两点和Z轴的旋转固体域进行计算，建立流动域与腔体域之间的网格连接，采用GGI连接方式。设置出口和入口的边界条件，入口采用总压模式，相对压力为零，出口采用平均静态压力，相对压力为1 Pa不考虑热传递、重力、浮力等因素的影响，初始条件设为静止流体。

4 仿真分析

设置压力、流量、流速等作为输出，进行了瞬态仿真分析，为了观察齿轮内流场的运动变化情况、吸入和排出腔体的流场运动情况，内部压力、流量的变化情况，这里对仿真结果进行分析。

(1)通过图3流场的速度矢量可以看出，液体从入口进入出口流出，验证仿真正确性。

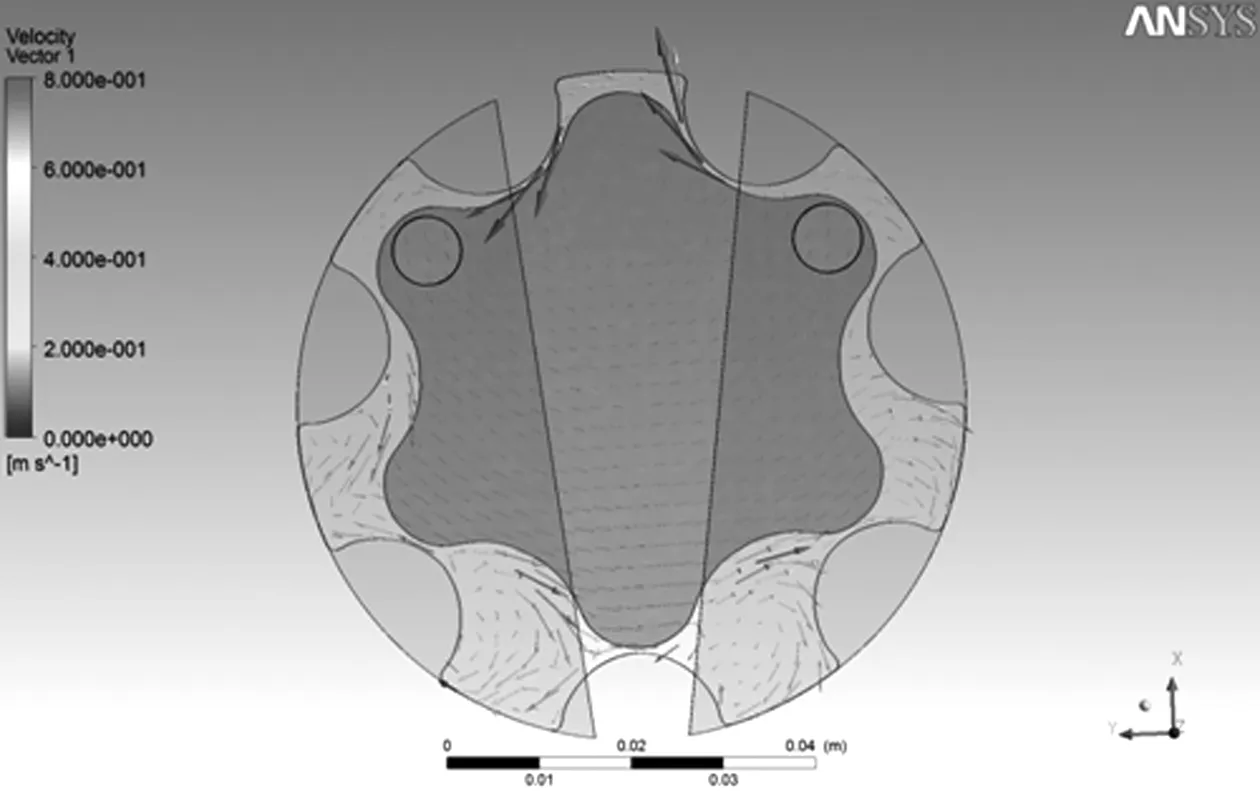
图3 内啮合齿轮泵流场的速度矢量图

(2)通过图4内啮合齿轮泵进出口流量的变化可以看出，流量变化随三个齿轮的运动呈周期性变化，并且进出口流量大小相等方向相反，验证了仿真结果正确，为内啮合齿轮泵排量评估提供依据。

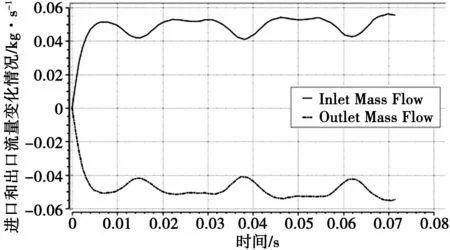
图4 内啮合齿轮泵进出口流量变化

(3)通过图5、图6内啮合齿轮泵内外齿轮的受力情况进行分析，其受力呈周期性变化，并且在初始起转过程受力最大，这与我们日常认识的情况一致，说明在进行齿轮结构动力学分析时只需验证第一个齿运动过程的变化情况即可。

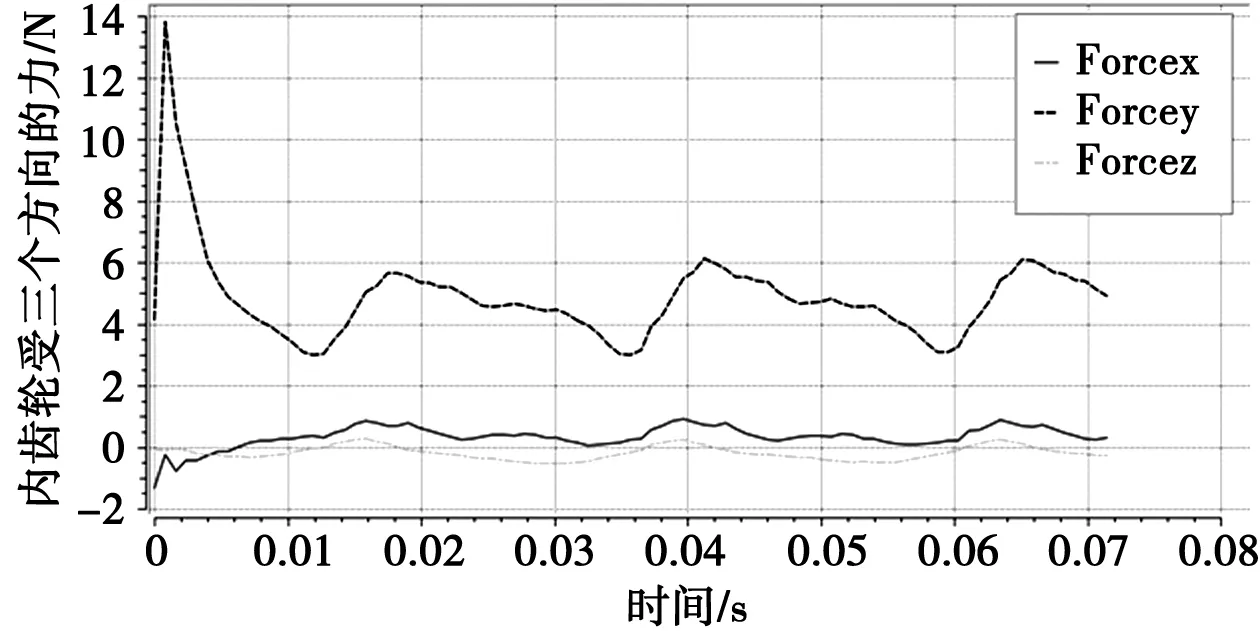
图5 内齿轮的受力变化情况

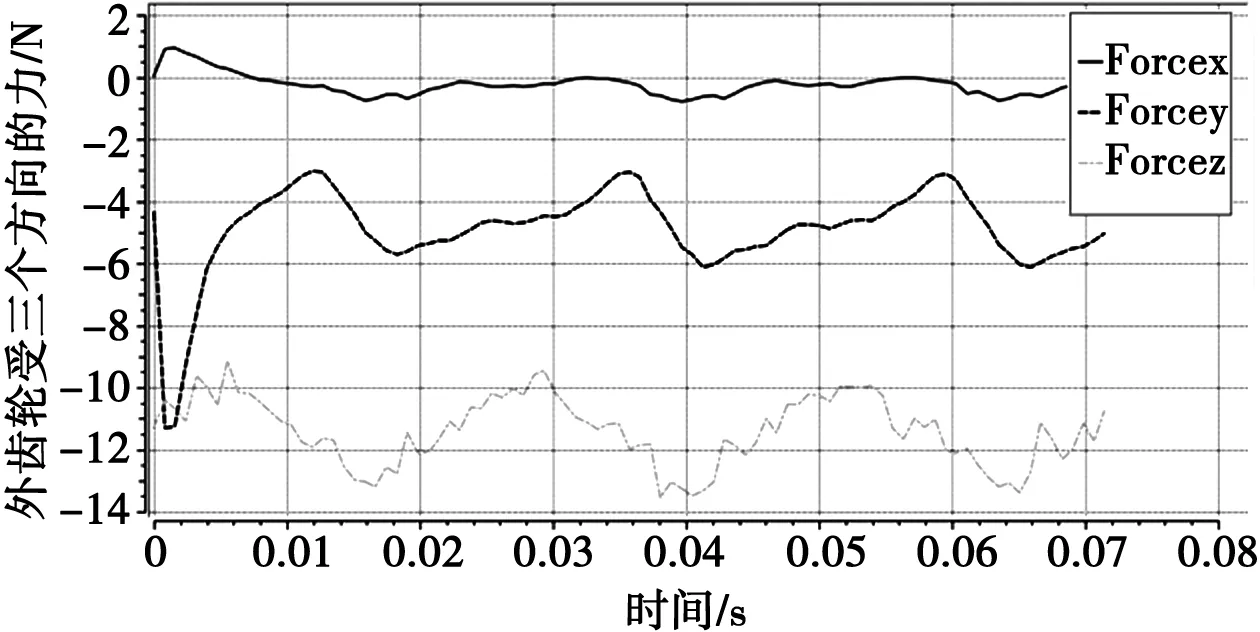
图6 外齿轮的受力变化情况

5 结论

本文通过对内啮合齿轮泵的内外齿轮、吸入和排出腔流场域的瞬态仿真分析，对容腔内部流动情况进行了分析，对流量变化、内外齿轮的受力情况进行了仿真分析，为内啮合齿轮泵的应用设计提供了相应的参考依据。