应急物资调度方案的优化问题研究
2021-04-01董玉玲刘小芳
董玉玲,刘小芳
(1.人工智能四川省重点实验室,自贡643000;2.四川轻化工大学自动化与信息工程学院,自贡643000;3.四川轻化工大学计算机科学与工程学院,自贡643000)
0 引言
广泛的应急物资的调度问题研究选取以地震灾害为例展开说明,原因为地震是危害力极大、发生率极高的自然灾害之一,同时,地震的发生也会影响着人类自身的生存与社会经济的持续发展[1],具有一定的可行性与相似性。自二十一世纪以来,里氏6.0级以上地震发生了1584次,平均113次。如青海玉树的7.1级地震,云南盈江的5.8级地震,新疆于田的7.3级地震,四川雅安的7.0级地震等。从科学技术层面而言,地震是不可阻止与避免的,为一定程度上减少高频地震灾害产生的损失,采取合理的应急资源调度方案已然成为应对突发地震灾害的必要措施,因此以震灾为例,对应急物资调度方案的优化问题研究具有较大意义。
在震灾物资调度决策问题上,关键在于物资运输的时效性、安全性和经济性三个分量函数之间的衡量抉择。针对车辆运输的特殊性,目前车辆运输问题(VRP)受到广泛关注与重视,若以运输成本最小化作为目标,Knott[2]提出的一个关于应急食品调度的线性规划数学模型,用作散装食品运输以及配送车辆队伍的效率提升,目标是使运输成本最低或者配送食品的数量最多;若以延迟时间最小化作为目标,何建敏[3]提出的在发生大规模震灾时,多出救点车辆调度的组合优化问题以满足受灾点的应急物资需求量;若以运输路径最小化作为目标,Fu[4]提出在旅行时间还没有确定的情况下,交通网络中的最短路径问题可以描述为动态随机最短路径问题(Dynamic and Stochastic Shortest Problem,DSSP),在网络中有部分或全部弧的旅行时间未固定而是无规律变化的,其概率分布在于抵达此弧的不同时刻,把随机过程作为描述交通网络中路径选择的参数。
因应急物资车辆路线选择问题相对复杂,所以使用指派问题中的旅行商理论方法,依据三个分量属性分别构造目标函数,随后通过无量纲处理和权重聚合赋权处理(组合赋权处理)转化为单目标函数,最后使用树算法求得理想目标函数值,以此获得最佳物资协调方案。
1 系统建模
应急物资的运输调度方案中选择运输路线问题实质上属于多目标决策问题,其主要决策问题是使多目标决策函数的三个分决策函数:时效性函数、经济性函数和安全性函数都达到最佳值(或理想值)然后确定其优先排列顺序。首先,通过每个方案的时效性函数、经济性函数和安全性函数使用无量纲处理的方法,随后通过组合赋权法使各个目标子函数融合在一个函数式子即得到决策效用函数。最后,为了选取最优路线调度决策方案,利用数算法求解目标决策函数的数学模型。
1.1 多目标函数的构造
在地震灾害发生时,对详细情况进行分析,若各物资存储点(或出救点)的应急物资能够满足各受灾点的需求,解决在满足需求的情况下,如何将各类应急物资从多个出救点运送至多个受灾点(或灾害点)。假定各受灾点需要的应急物资数量未知或因道路、天气等外界因素导致的运输时间不确定性。因此,将震灾爆发后的应急物资运输方案的选择问题可描述为:假设现在考虑某一种应急物资“棉被”需要调配,已知可供应“棉被”有D1,D2,…,Dm的m个库存点(如地震应急物资储备库所在地),需要“棉被”有S1,S2,…,Sn的n个受灾点。假设在时刻t,需要将应急物资“棉被”从库存点i运送至受灾点j,其中受灾区j的人员受伤死亡密度为Rj,所对应的运输成本为Pij,运输时间为Tij,选择的应急物资调度优化方案应当满足以下要求:每个存储点应提供应急物资的数量为多少,分别运送至哪些灾害点,当Di=0则说明第i个存储点不参与此次应急物资的运输,应急物资运输目标应该在满足各受灾点的应急物资需求作为前提,使得时间最短或伤亡密度最大或成本最低。即多目标函数的表示为:

1.2 决策效用函数数学模型的构造
假设在地震灾害的应急物资运送问题中,时效性、安全性和经济性三者互相独立,利用其独立且互相不影响的特性,将多目标决策效用函数转换为单目标效用函数的加法函数[5]。即可将决策效用函数表示为目标分量得无量纲指标加法函数。因此,对时效性分函数、经济性分函数和安全性分函数三个子目标函数通过无量纲处理的方法,得到各分量函数的理想数值(最大值或最小值),完成求解多目标决策函数的第一步。
针对时效性函数中的时间分量,使用Dijkstra算法在道路网络图上求出理想值即最短时间和最长时间。假定在地震发生后,应急物资从存储点i运送至受灾点j,所需要的时间表示为Tij,因此,最短时间为Tmin,最长时间为Tmax,g(i1j)为运输时间Tij的无量纲指标,表达式如下:

因为Tmin≤Tij≤Tmax,则时间的无量纲指标g(i1j)∈(0,1),而Tmax-Tmin的值是固定不变,Tij的值越小,则分子Tmax-Tij的值越大,即g(i1j)的值越大,代表运输时间越短或时效性函数越佳的运输路径,对应的无量指标g(i1j)越大[6]。
同理可得,设应急物资从存储点i运送至受灾点j,运输成本表示为Pij,g(i2j)为运输费用的无量纲指标。因此,最低运输费用为Pmin和最高运输费用为Pmax,表达式如下:

由于Pmin≤Pij≤Pmax,由上式可得,运费的无量纲指标g(i2j)∈(0,1),而Pmax-Pmin的值固定不变,Pij的值越小,则分子Pmax-Pij的值越大,即g(i2j)的值越大,表明g(i2j)的值越大就选运输费用越低的条件相契合。
针对安全性函数中的人员伤亡分量,利用数据融合技术统计应急物资从受灾点i运送至受灾点j的人员伤亡密度,设g(i3j)为受灾点j的伤亡密度无量纲指标,最大伤亡密度表示为Rmax,最小伤亡密度表示为Rmin,与此同时,为保持与其他两个分量无量纲指标的一致,g(i3j)的值越大越好,换句话说,随着人员伤亡分量或伤亡密度R的值越大,g(i3j)的值越大,即安全性函数越好。则表达式如下:

假设α1、α2、α3表示应急物资调度管理的时间性决策函数、经济性决策函数、安全性决策函数这三个分量决策函数的权重,其权重向量为α=(α1,α2,α3)T,满足0≤α1≤1,0≤α2≤1,0≤α3≤1,α1+α2+α3=1,设Gij为运输线路的决策效用指标,则相应路径选择的决策效用函数数学模型如下所示:

由上所得,若Gij的数值越大,物资运输路线的综合评价性指标越高即效果越佳,所以选取Gij值最大的应急物资运输路径(从存储点i运送至受灾点j)为最终决策。
2 加权处理
目前,确定权重主要有三类方法:组合赋权法(主客观综合赋权法)、主观赋权法以及客观赋权法。主观赋权法是依据决策者(或专家)对每类属性的主观关注度来确定权重。如专家调查法(Delphi法)、二项系数法及层次分析法(AHP法)等[7]。客观赋权法是依照各目标函数的原始数据间的关系,不依靠人的主观偏好来确定权重。如主成分分析法、均方差法及熵法等。
结合主、客观赋权法各自的优缺点,以及决策者(或专家)对赋权法的偏好度和赋权法原始数据的一致性程度是相对合情合理的,使对权重的确定达到主观方面与客观方面的互相统一,得到的最终决策结果更加真实有说服力,提出了一类综合主、客观赋权优点的方法,即组合赋权法。
2.1 数据预处理
假设有n个决策方案,其方案集合表示为B={B1,B2,…,Bn},决策目标有m个,其指标集表示为U={U1,U2,…,Um},方案Bj=(j=1,2,3,…n)在决策目标Ui=(i=1,2,3,…m)下的属性值为λij,决策矩阵(或属性矩阵)为B=(λij)m*n。通常,目标类型有效益型与成本型。效益性目标表示正比型指标(即效益值越大越好的指标),成本性目标表示反比型指标(即成本值越小越好的指标)。由于各目标属性具有不同的量纲与量纲单位,由此具有的不可公度性将会对决策结果有一定影响,此前,应将目标属性指标做预处理,即通过无量纲处理将决策矩阵(或属性矩阵)化为规范化矩阵。(λmjax、λmjin分别表示决策目标j的最大和最小值。)设效益型目标为:

可以看出,rij∈[0,1],1≤i≤m,1≤j≤n,所以规范化矩阵为:R=(rij)m*n
结合主、客观权重赋权法的利弊,可以考虑组合的赋权方法ω=(ω1,ω2,ωm)T,称ω为集成后的权重向量,ωˉ"、ωˉ*分别称为主、客观综合权重,其表达式如下:

首先是主观权重赋权法,由于各个决策者(或专家)在根据对每个目标属性的重视程度进行赋值时,难以兼顾每一个目标属性之间的互相影响与制约[8],所以在决策者(或专家)在给出一般情况下的决策权重为ω=(ω1,ω2,ω3,…,ωm)T后,引 入 目 标 影 响 权 重[9]为ω(2)=(ω1(2),ω2(2),…,ωm(2))T。设xij是表示目标Ui对目标Uj的影响程度,则有目标相互影响矩阵为:X=(xij)m*n,而表示目标Ui对其余目标的影响度,而表示目标Uj对其余目标的影响度。
因此,由目标之间相互影响度所得到的权重为:

若不考虑目标间的影响程度只考虑目标本身的价值权重为:

比较以上两式可得,式(9)综合考虑到了目标的价值权重,这表明在一个目标对价值权重的重要程度上相对较高或称为有较大影响力,则其影响的权重也会随之相对较高。综上两种权重的表达式,能够全方位的反映出一个目标的相对重要程度属性,假设λ为目标价值权重与目标影响权重的比例因子,且0<λ<1则有主观综合权重为:

同时,对目标之间相互影响所得到的权重、目标本身的价值权重及主观权重为:


2.2 主客观权重的集成与评价
假设θ1、θ2分别为主、客观权重的重要程度指标系数(或组合权系数向量的线性表出系数)且θ1+θ2=1,θ1>0,θ2>0,将主观权重ωˉ"与客观权重ωˉ*集和组成即代入式(8)有:

从上式可以看出,集成后的权重向量包括主观权重即反映决策者(或专家)的偏好的权重和目标间相互影响的权重,以及客观权重即反映原始数据属性的权重,从而使权重的确定更加精准。
2.3 构建单目标函数数学模型
(1)树算法
分配问题又可以看做为指派问题,即将m项任务分给n个人的指派问题,每人只能完成一项任务,且每个任务只能由本人独立完成,第i个人单独完成第j项任务的效益为cij,如何才能使总效益值达到最小?[12]由文献[13]可以清楚知道树算法的基本思想,即在完整指派树中每片树叶有相对应一个指派方案,共有n!个树叶,最优指派方案就是从所有树叶中找出数值最小的树叶,逆向追踪得到的指派方案。
(2)数学模型的构建
分配问题或指派问题的求解通常是匈牙利算法,但是其解法步骤复杂、不实用,所以选择优化改进或找寻其他简易方法,树算法是简易中的其中一种。由上述介绍可以推出,树算法也可运用于运筹学[14]中的最优匹配问题或最优指派问题,所以,利用此特性能将决策效用函数矩阵类比于树算法中的效益矩阵,得到最佳应急物资调度方案,则有数学模型如下所示:

在指派问题中,xij=1/0,1表示指定第i个人完成第j项任务,0表示不指定第i个人完成第j项任务,在本文来讲,xij=0是表示运输路线不经过路段(i,j),xij=1是表示物资运输路线经过路段(i,j),在运算求解最大效益值fmax(xˉ)的过程中就能得到最佳调度路线方案。
3 案例分析
假设某城市发生突发性强烈地震灾害,现在需要将应急物资从存储点运送至受灾点,设现有四个存储点D1、D2、D3、D4和四个受灾点S1、S2、S3、S4,从存储点Di到受灾点Sj,对应的运输成本为Pij,配送时间为Tij,其中在发生地震的第5小时后,受灾区j的人员受伤死亡密度为Rj,如表1-表3。

表1 运输成本表(千元)

表2 配送时间表(小时)
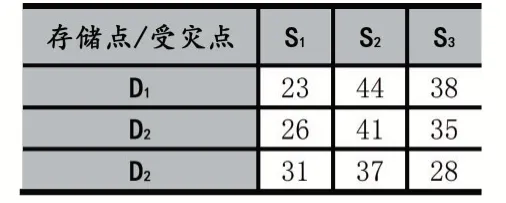
表3 人员受伤死亡密度(个/1万平方米)
3.1 无量纲处理
由式(2)、(3)、(4)可得无量纲处理后的数值,如表4-表6所示。

表4 运输成本表(千元)

表5 配送时间表(小时)

表6 人员受伤死亡密度(个/1万平方米)
3.2 加权处理
针对三个存储点D1、D2、D3和三个受灾点S1、S2、S3其方案集有6个,分别表示为F1(D1→S1,D2→S2,D3→S3),F2(D1→S1,D2→S3,D3→S2),F3(D1→S2,D2→S1,D3→S3),F4(D1→S2,D2→S3,D3→S1),F5(D1→S3,D2→S2,D3→S1,F6(D1→S3,D2→S2,D3→S1),评估目标有三项:时效性是U1、安全性是U2及经济性是U3,同时,专家给出的权重表示为:ω=(0.45,0.28,0.27);其中0代表无影响、2代表较小影响、4代表一般影响及8代表较大影响,则有目标相互影响矩阵为:

而且U1、U3为成本型目标,U2为效益性目标,则经无量纲处理后的规范化矩阵如下所示:(说明:属性值取无量纲处理后每一个方案Bj(j=1,2,3,…,n)在决策目标Ui(i=1,2,3,…,n)下的属性值λij的平均值作为规范化矩阵)。

然后,由式(10)和式(11)可得主观权向量ωˉ",取λ=0.5,其表达式如下:
ωˉ"=(0.4199,0.3242,0.2558)T
由式(18)可得客观权向量ωˉ*,则有表达式为:
ωˉ*=(0.3964,0.3559,0.2477)T
假设主、客观权重的重要程度相同,即θ1=θ2=0.5,由式(19)可得集成后的权重为:
ω=(0.4082,0.3401,0.2518)T
所以三个分量决策函数的权重分别为α1=0.4082,α2=0.3401,α3=0.2518,由式(5)可得决策效用指标函数Gij,则如表7所示。

表7 决策效用指标函数Gij

利用树算法求解[]计算其他分枝,根据简化指派树得最大效益值,可得最优方案为方案F2(D1→S1,D2→S3,D3→S2)。
4 结语
本文依据震灾发生后的应急物资运输的时效性、伤亡性和经济性三大特性解决多目标决策问题,利用无量纲处理和将决策者(或专家)的偏好因素、决策目标间互相影响因素与客观因素最大程度集成在一起的主客观赋权法确定目标权重,再经构造决策效用指标函数使多目标决策转化为单目标,最后,通过树算法转化为极小值问题求解最值的过程中找到最佳路线匹配,求得最佳的震灾应急物资调度方案。以此震灾的应急物资调度方案研究可推论至广泛的应急物资调度问题研究,具有相对可行性与有效性,但优越性还需再深入研讨。
