基于互补原理确定黄土高原Budyko方程的流域特性参数
2021-03-31韩松俊邵薇薇
韩松俊,邵薇薇
(中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038)
1 研究背景
蒸散发是流域水循环的重要过程,对水文模拟、灌溉用水管理和效率评估等都具有重要意义[1-2]。Budyko[3]在进行全球水量和能量平衡分析时发现,陆面长期蒸散发量主要由陆面水分供给(降水量)和大气蒸发能力(潜在蒸散发量)之间的平衡决定,由此提出的Budyko(水热耦合平衡)方程被广泛应用于流域年或多年尺度实际蒸散发量的估算[4-5]。Budyko方程中的唯一参数应与流域下垫面地形、土壤和植被等条件有关[5-7],被称为“流域特性参数”。分析流域特性参数的变化特征和获取方法是基于Budyko方程进行流域实际蒸散发估算的关键,对分析土地利用变化的径流响应也具有重要意义[7-8]。傅抱璞[6]推导出了利用降水强度和径流系数确定流域特性参数的经验公式以考虑地形、土壤、植被等因素,张橹等[5]分析了不同植被类型的影响。杨大文等[4,9-10]利用我国非湿润地区108个小流域的长期气候和流量资料,将流域特性参数与相对入渗能力、相对土壤蓄水量、平均坡度以及植被覆盖度建立联系。人类活动也是流域特性参数的一个重要影响因素,韩松俊等[11]分析了灌溉面积比例对塔里木河流域绿洲灌区Budyko方程参数的影响,王卫光等[12]分析了人口状况、生产总值和有效灌溉面积对黄河流域Budyko方程参数的影响。但受数据限制,长序列的土地利用和植被变化数据不易获取[13],成为开展相关研究的一个主要障碍。
由于陆面与大气之间的相互作用,陆面的水分状态和植被覆盖等变化会对区域气候产生影响,互补原理据此利用常规气象数据间接表征下垫面特征,成为区域蒸散发研究的一种思路[14-15]。互补原理假定,在一定的辐射能量输入下,当充分供水时实际蒸散发量与潜在蒸发量相等,为陆面充分湿润状态下的蒸散量,当陆面供水量减少时,实际蒸散发量减少并释放出更多的能量,使近地面气温、湿度等气候特性发生改变,并导致潜在蒸发量增加。所谓“互补关系”指潜在蒸发量的增加量与实际蒸散量的减少量大小相等,后来假设其为一定线性比例。韩松俊等[16-17]突破实际蒸散发量与潜在蒸散发量之间的线性互补关系,但保留其核心思想,即通过大气状态的变化间接确定干湿状态和植被状况等下垫面特征的变化,并确定了Penman潜在蒸发中辐射项所占比例这一关键指标,提出了基于非线性函数的广义互补原理。既然基于互补原理可以利用常规气象数据间接表征下垫面特征,那么有没有可能利用其确定Budyko方程中的流域特性参数,以解决研究中长序列土地利用和植被变化数据不易获取的难题?
本文针对黄土高原地区29个小流域,分析互补原理中Penman潜在蒸发中辐射项所占比例这一指标与Budyko方程流域特性参数的关联,建立利用常规气象数据确定流域特性参数的方法,并应用于对流域实际蒸散发量的估算。
2 黄土高原Budyko方程的流域特性参数研究数据和方法
2.1 研究区域与数据 本研究采用的黄土高原地区29个小流域主要分布在黄河干流以及窟野河、无定河等支流(图1),受大坝水库和外流域调水等人类活动影响较小。流域面积介于283~29 662 km2之间,流域边界由1 km的DEM提取。
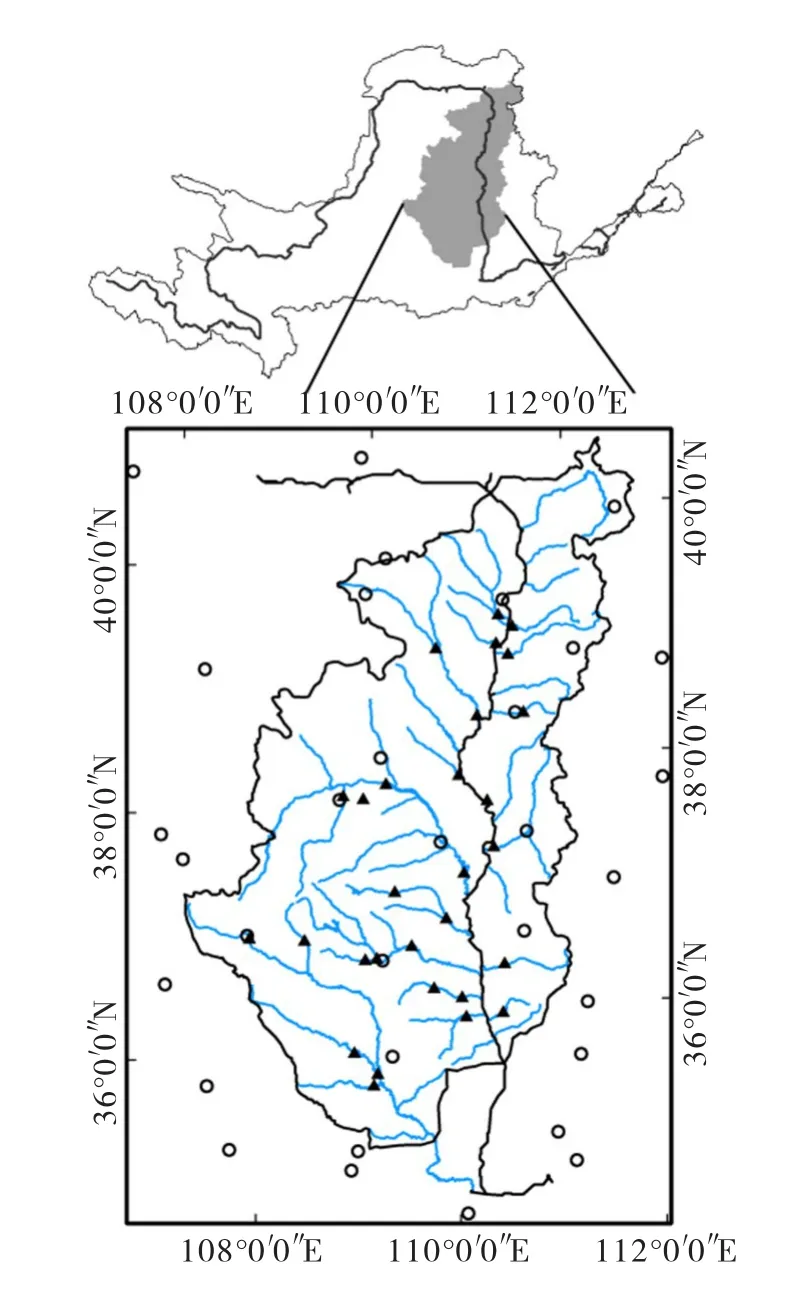
图1 研究中采用的黄土高原地区29个小流域分布(▲为流域出口位置,○为气象站位置)
研究中用到的1956—2000年间的流域出口的月径流数据来源于水利部水文局,29个流域径流数据时间序列长度介于6~46年,平均为25.6年。研究所用到的气象站点数据来源于国家气象信息中心,包含从1956到2000年的每日降水,气温,日照时间,风速和相对湿度等。研究中用到的植被覆盖度由1982—2000年NOAA-AVHRR全球数据库的1 km精度月归一化植被指数计算得到。通过假设流域蓄水量变化值为零,根据水量平衡计算获得各小流域多年平均和年实际蒸散发量[4,10]。通过将站点气象数据采用距离方向加权平均法(气温采用高程修正的距离方向加权平均法)插值到10 km网格,然后利用Penman公式计算每个网格的日潜在蒸散发量,最后计算流域平均降水和潜在蒸散发量。
2.2 研究方法 研究中采用的Budyko方程[18]为
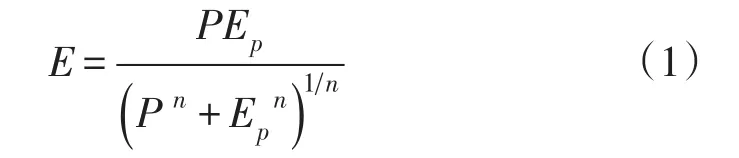
式中:n为流域特性参数,前期研究主要利用土壤相对入渗能力、流域平均坡度以及植被覆盖度确定其大小;P为降水量;Ep为潜在蒸发量,本研究中由Penman公式计算,由辐射项与空气动力学项两部分组成:

式中:Erad和Eaero分别为Penman潜在蒸发量EPen的辐射项和空气动力学项;Δ为饱和水汽压梯度;γ为湿度计常数;Rn为净辐射量,通过太阳辐射确定;G为土壤热通量,当计算尺度为天时取值为0;e*(Ta)为气温Ta下的饱和水汽压;RH为相对湿度; f(u)为风速的函数,采用1979年联合国粮农组织推荐的改进函数形式。
在太阳辐射输入一定的情况下,Penman潜在蒸发量(式(2))中的辐射项相对稳定,而空气动力学项随下垫面变化较为显著。韩松俊等[19]在非线性广义互补原理中,利用Penman潜在蒸发中辐射项所占比例间接表征下垫面特征,将蒸散发比表示为的非线性函数:

Erad/EPen被称为“大气湿润指数”,是互补原理研究中的关键指标,本研究分析其与植被覆盖度等流域下垫面特征之间的联系,尝试建立通过其确定流域特性参数的方法。
研究中利用绝对偏差MAE、均方误RMSE和NSE为效率系数评价Budyko方程对实际蒸散发量的模拟效果,其中NSE为效率系数可表示为:
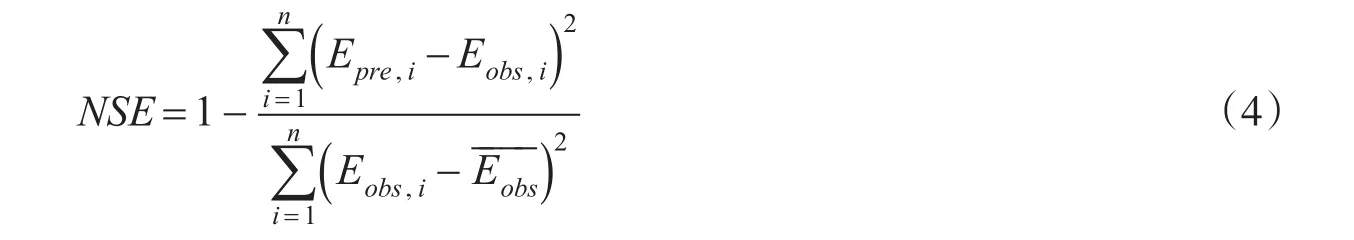
式中:i为时间序列,n为时序长度;Epre,i和Eobs,i分别为实际蒸散发量的估算值和实测值。
3 结果与讨论
3.1 Budyko曲线与下垫面特征 研究区属于干旱半干旱地区,29个小流域多年平均降水量P在345~600 mm之间,实际蒸散发量在303~570 mm之间,而潜在蒸发量EPen在943~1157 mm之间。按照Budyko曲线的两种等价形式,将29个小流域多年平均蒸发量(E)、潜在蒸发量(EPen)与降水量(P)点绘于图2。流域多年平均随着显著增大,拟合得到的Budyko方程(1)的参数n=2.31。在相对湿润的流域(P/ EPen较大),植被覆盖度(M)较高,而蒸散发比E/ EPen也较大,显示出研究区植被覆盖度对Budyko曲线的显著影响[10]。
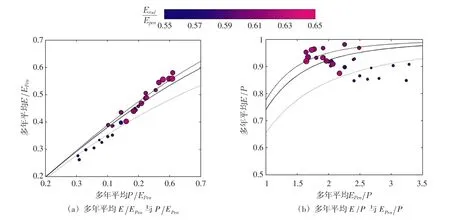
图2 黄土高原29个小流域的Budyko曲线
研究区29个小流域的植被覆盖度M在0.08~0.50之间,图3显示出流域植被覆盖度与气候变量之间具有一定的相关性,降水量大、潜在蒸发量EPen小的流域具有较大的植被覆盖度。为了分析植被覆盖度M与水量平衡和气候特征之间的联系,将29个小流域分成2组:14个小流域M<20%(均值为11.9%)而15个小流域M≥20%(均值为35.1%)。M<20%的小流域多年平均降水量(428 mm)和实际蒸散发量(382 mm)明显低于M≥20%的小流域(分别为523和490 mm),而M<20%的小流域多年平均潜在蒸发量(1066 mm)高于M≥20%的小流域(1007 mm)。对两组小流域分别拟合Budyko方程的参数,M<20%的小流域的流域特性参数(n=1.64)明显小于M≥20%的小流域(n=2.74)的参数。
3.2 植被覆盖度与大气湿润指数的关联 表1中的两组小流域辐射项均值相同,说明其多年平均潜在蒸发量差异来自于空气动力学项,受此影响,M<20%的小流域的大气湿润指数Erad/EPen(均值为0.58)小于M≥20%的小流域(均值为0.62)。从图3中也可以看出29个小流域的植被覆盖度M与大气湿润指数Erad/EPen具有较好的相关性。图3(a)中进一步给出了29个小流域M与Erad/EPen关系,M随着Erad/EPen的增大而增大。

表1 黄土高原29个小流域不同分组的气候特征以及拟合的流域特性参数n
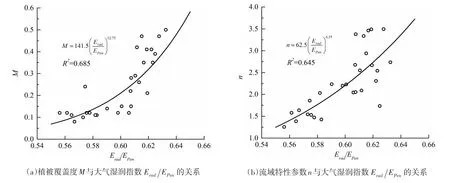
图3 黄土高原29个小流域植被覆盖度M和流域特性参数n与大气湿润指数Erad/EPen的关系
3.3 流域特性参数与大气湿润指数的关系 考虑到植被覆盖度M是确定流域特性参数n的重要指标,而植被覆盖度M与大气湿润指数Erad/EPen具有很好的相关性。因此,在P/EPen一定的情况下,流域植被覆盖度M越高,E/EPen和大气湿润指数Erad/EPen都越大。图2中也可以看出,Erad/EPen越大,Budyko曲线越往上移,表明流域特性参数n值越大。从图3(b)中可以看出,n值随着Erad/EPen的增大而增大,具有较为显著的相关关系,可以采用幂函数公式进行拟合:

通过式(5)建立流域特性参数n值和大气湿润指数Erad/EPen之间的关系,能够在不采用植被覆盖度等下垫面数据的情况下,利用常规气象数据间接确定流域特性参数n值的大小。
3.4 流域实际蒸散发量模拟 根据式(5)利用多年平均大气湿润指数Erad/EPen确定流域特性参数,然后代入Budyko方程(1),模拟得到的流域多年平均实际蒸散发量与水量平衡结果的对比见图4。相比固定流域特性参数,通过式(5)确定流域特性参数提高了对流域多年平均实际蒸散发量的模拟效果,其中绝对偏差MAE和均方根误差RMSE分别由21.51和25.74 mm降低到12.64和15.29 mm,而纳什效率系数NSE由0.87提高到了0.95。

图4 多年平均实际蒸散发量与水量平衡结果对比
进一步针对两个典型流域评价利用大气湿润指数Erad/EPen确定流域特性参数,对流域实际蒸散发量年际变化的模拟效果。采用两种方法来进行比较:(1)使用优化得到的固定n;(2)根据逐年变化的大气湿润指数Erad/EPen计算逐年的n。模拟结果显示(图5),采用Erad/EPen计算的逐年变化的参数n的结果优于采用固定参数n的结果,与水量平衡得到的实际蒸散发数据拟合得更好,在年际变化上,在高值和低值的模拟上比采用多年平均的结果略有改善,能相对较好地反映出实际蒸散发量在年际的波动。
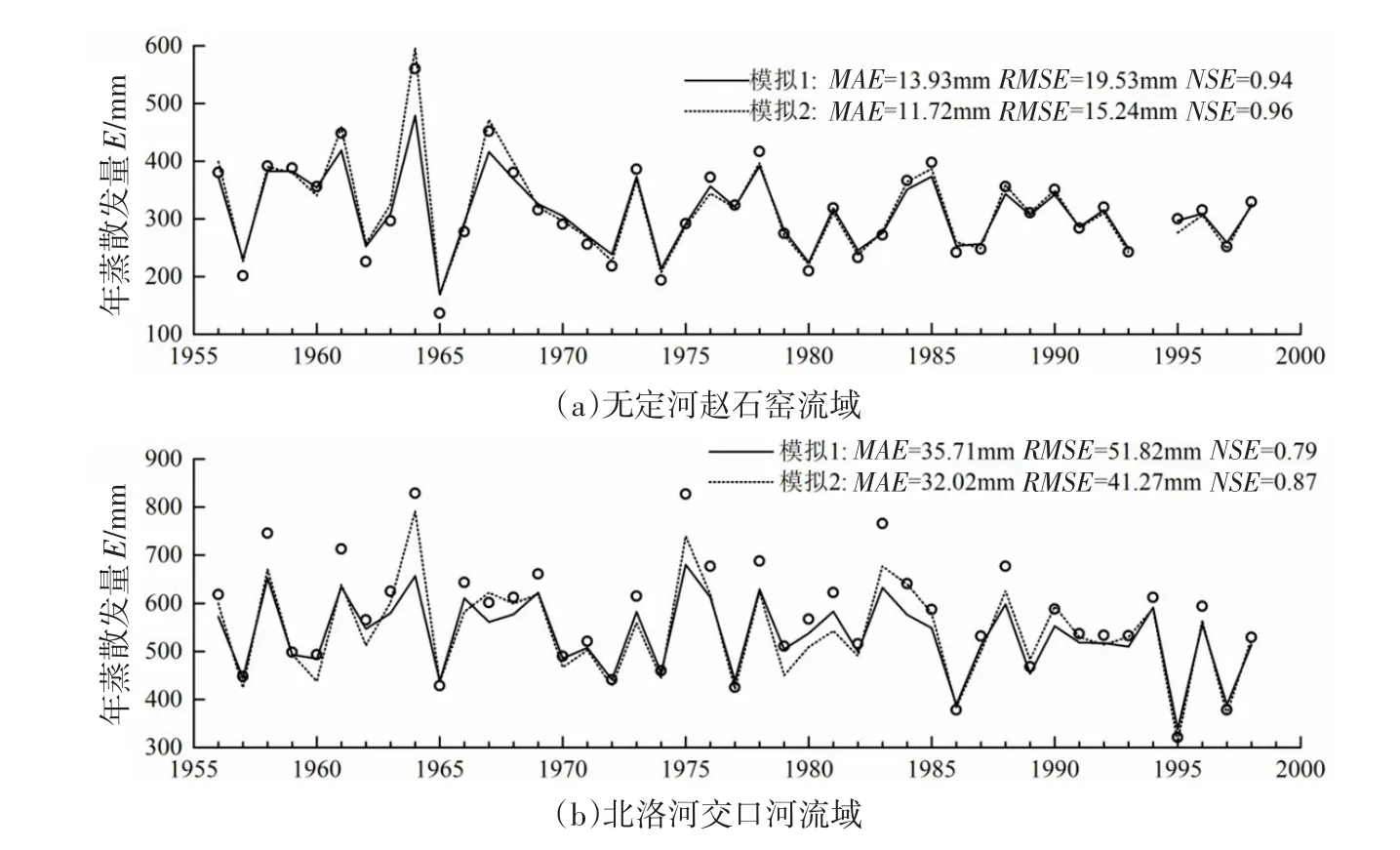
图5 用两种方法模拟的流域实际蒸散发量
采用式(5)能够利用常规气象数据计算流域特性参数n自1956年开始的变化,而由于数据限制利用植被覆盖度只能计算1982年之后n的变化,因此相比利用植被覆盖度等下垫面数据的方法,这种方法具有数据容易获取且时间序列比较长的优点。另一方面这种方法在某种程度上实现了互补原理与Budyko方程的耦合,能够考虑潜在蒸发中的辐射项和空气动力项对流域实际蒸散发的不同影响,有利于准确认识气候与下垫面的协同变化规律,更准确揭示研究区蒸散发变化机制。
4 结论
本文以黄土高原地区29个小流域为研究对象,分析了流域植被覆盖度与互补关系中大气湿润指数之间的关联,发现大气湿润指数可以间接表征研究区流域植被覆盖度的变化,进而可以间接反映Budyko方程中流域特性参数的变化,提出了基于互补原理利用常规气象数据确定Budyko方程的流域特性参数的方法。主要得到了以下一些结论:
(1)通过分析植被覆盖度和大气湿润指数在Budyko曲线上的分布,发现由于陆面和大气之间的相互作用,黄土高原地区的植被覆盖度与大气湿润指数之间存在关联,在相对湿润的环境中,植被覆盖度更大,大气湿润指数Erad/EPen更大,蒸散发效率更高。
(2)利用植被覆盖度与大气湿润指数Erad/EPen之间的关联能够建立流域特性参数与大气湿润指数之间的关系,研究中采用幂函数公式进行了拟合,取得了较好的效果。
(3)基于互补关系利用大气湿润指数Erad/EPen确定Budyko方程的流域特性参数n,能够间接反映植被覆盖度等下垫面因素对流域水热耦合平衡的影响,且具有时间序列更长、数据更易获取的优点,引入大气湿润指数逐年变化后,改善了对流域蒸散发长序列年际变化的模拟效果。
