基于BP神经网络的活性粉末混凝土（RPC）强度预测研究

胡顺新 殷 琪

（广西理工职业技术学院，广西 崇左 532200 ）

0 引言

超高性能混凝土—活性粉末混凝土（Reactive Powder Concrete，简称RPC），因其强度高、韧性好、耐久性能好等优点[1-2]，它的应用可有效解决存在于普通混凝土结构中的难题。而RPC的强度指标对于其实际工程应用有着非常重要的影响，而目前仍处于试验研究阶段，缺乏相应的强度计算分析模型。

BP神经网络模型是一种在工程应用广泛且具有优质泛化能力的前馈型神经网络[2][3]，本文拟借助 BP 神经网络方法，在进行配合比试验的基础上建立 RPC 强度的预测模型。并利用该模型系统研究水胶比、钢纤维掺量以及硅灰掺量比等影响因素对于 RPC强度的影响，进而为RPC的强度预测及配比设计提供参考。

1 试验及试验现象

1.1 原材料

水泥：为了推广RPC的应用，本试验选用水泥为市场上常见的42.5级普通硅酸盐水泥；硅灰技术指标如下：堆积密度235kg/m3，比表面积20000m2/kg，平均粒径0.1～0.2μm，SiO2含量94.7%；石英砂：为了保证RPC的密实度，选取以下三个等级的石英砂：粗粒径砂（1.25～0.63mm）、中粒径砂（0.63～0.315mm）和细粒径砂（0.315～0.16mm），使用时按一定的1:4:1的比例掺配；减水剂：RPC水胶比低，本试验选用聚羧酸系高效减水剂，减水率为30%；钢纤维：根据国内外对掺钢纤维的活性粉末混凝土的研究，长径比宜选取50 ～ 80mm。

1.2 试件设计

本次试验共设计了16组配合比编号如表1所示，用以研究水胶比、砂胶比、钢纤维体积掺量以及硅灰掺量比例4个主要影响因素对RPC抗压、折强度的影响，试验结果见表1。

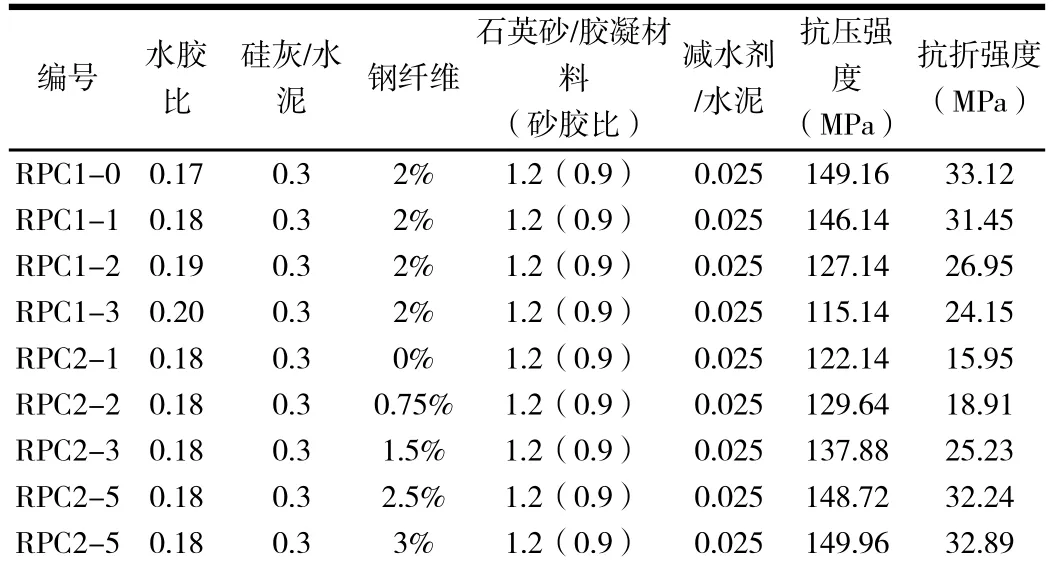
表1 RPC 试验配合比及其对应强度结果表

注：钢纤维为体积比，其余材料均为质量比

2 强度影响因素分析

（1）水胶比：对表1 中RPC1-1～RPC1-3 结果对比分析 可得，当水胶比由0.17 上升至0.18、0.19、0.20 时，抗压强度降幅分别为2.0%、14.8%、22.8%，抗折强度降幅分别为5.0%、18.6%、27.1%；可见水胶比上升会使得RPC 的抗压、折强度均有所降低。可见水胶比是影响RPC 强度的重要参数。

（2）钢纤维体积率：对比RPC1-3 及RPC2-1～RPC2-4 的结果可知钢纤维掺入RPC 可使抗压、折强度均有所增强。RPC1-3 及RPC2-2、RPC2-3、RPC2-4 的钢纤维体积分别为0.75%、1.5%、2.0%、3.0%相较于钢纤维掺量为0%的RPC2-1。相应的抗压强度增长率为6.14%、12.88%、21.78%、22.78%，抗折强度增长率为18.56%、58.18%、102.13%、106.21%。故钢纤维掺入对RPC 抗压、折强度的增强有正向的提升作用。

（3）硅灰掺量：本试验的硅灰掺量与水泥的比例范围为10%～40%。硅灰的掺入首先充分填充水泥颗粒之间的孔隙和起到润滑的作用，并且硅灰中的SiO2可以充分消耗对RPC 强度不利的Ca（OH）2晶体，其次硅灰的加入有利于钢纤维与基体之间的粘结，使钢纤维和基体界面粘结力达到最大[4]。

（4）砂胶比：RPC 基于最大密实堆积理论进行配制，无粗大颗粒的卵石，石英砂则成为RPC 最主要的骨料。虽然石英砂不具备活性不参与水泥浆体的水化反应、但其与胶凝材料的比例会影响RPC 内部的均匀性及骨料相及浆体相的强度进而对RPC 的抗压、折强度能产生影响[5]。

3 RPC 神经网络建立及预测

RPC 是在最大密实堆积理论的前提下配制而成的，并且有活性成分硅灰及钢纤维的加入进一步优化了RPC 的微观结构。基于RPC 的强度机理若仍旧采用传统的包米尔公式对RPC 的强度进行预测将会超生较大的误差，这将不利于RPC 在实际工程中的应用。本文拟建立两个BP 神经网络模型分别对RPC 的抗压强度及抗折强度进行预测

3.1 神经网络设计

在采用BP 神经网络解决实际问题时需要对模型结构及相关参数进行选择和确定。对于本次建立的RPC 强度预测模型，输入层节点数为4，即钢纤维体积率、水胶比、砂胶比、硅灰掺量4 个影响因素节点；输出节点数则为1，即RPC 立方体抗压强度（或抗折强度）。4.2 BP 神经网络的样本选取及数据处理

（1）样本选取：根据表1 的试验结果，选取RPC1-2、RPC1-2 及RPC1-2为测试样本，其余数据为训练样本。

（2）数据处理：为提高模型的泛化能力及训练效果在进行训练样本前对所有数据进行“归一化”处理将数据均转化成无量纲数。

3.2 网络模型训练

根据本文4.1～4.2 节相关分析，采用Matlab 神经网络工具箱对网络进行建立。网络最终的拓扑结构为[4-13-1]；选用tansig-logsig 函数组合作为本模型的传输函数；训练函数为trainlm；学习速率设定为0.01；误差限值设定为0.0001；最大训练次数为1000[6][7]。由于本模型的训练函数为trainlm，数据收敛速度较快，在进行13 次后既到达误差所需的目标限值，完成网络建立。

3.3 BP 神经网络预测结果分析

将未参与训练的三组测试样本（RPC1-2、RPC1-2 及RPC1-2）输入已建立完成的神经网络中即可得到预测结构，将预测结构与试验结果进行误差分析见表2。

表2 RPC 抗压、折强度预测结果表

由表2 可知，采用本文建立的BP 神经网络模型分别对RPC 的抗压、折强度进行预测，其最大、最下小相对误差分别为4.78%和1.14%，最大相对误差仅为4.78%满足工程精度要求。

4 RPC 强度参数分析

由上述的误差分析结果可知，本文建立的BP 神经网络模型是切实有效的，因此可将其运用到各主要因素对RPC 强度影响的分析当中去。只需将所要预测的样本数据转化为矩阵输入到训练完成的BP 网络中，待网络完成运算后即可得到预测结果。图1～图4 为利用本文建立的BP 网络分析得到的钢纤维体积率、水胶比、沙胶比及硅灰掺量对RPC 强度的影响结果。

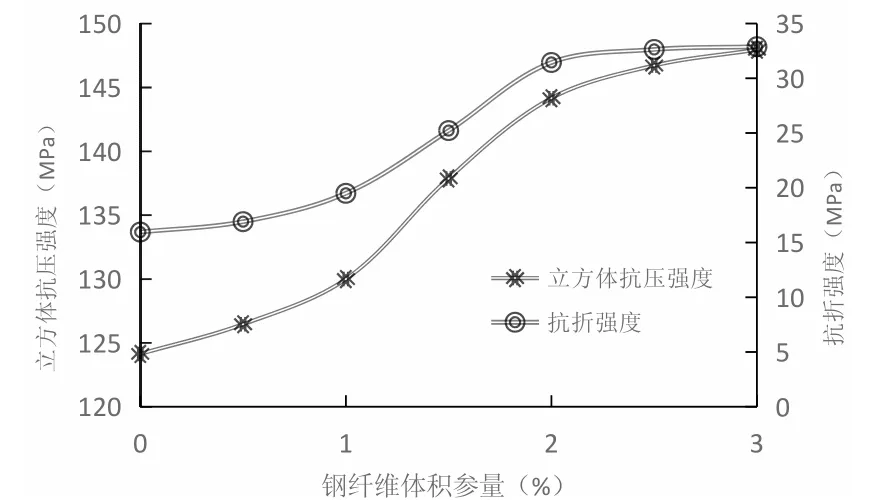
图1 钢纤维体积掺量对RPC 抗压、折强度的影响

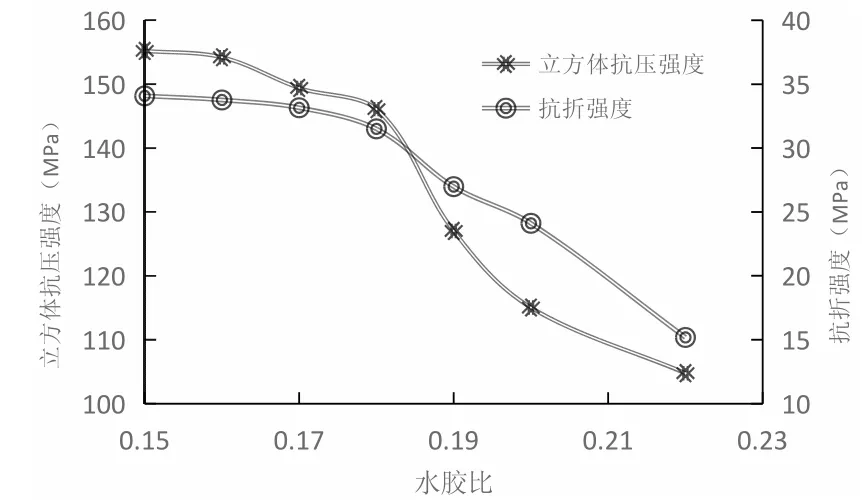
图2 水胶比对RPC 抗压、折强度的影响

图3 硅灰掺量对RPC 抗压、折强度的影响

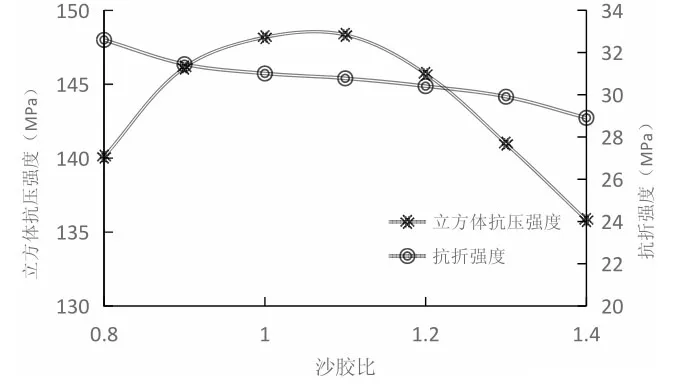
图4 沙胶比对RPC 抗压、折强度的影响

不同钢纤维掺量对RPC 抗压、折影响曲线见图1。由图中曲线可知，当钢纤维含量<1%时，其对RPC 的抗压、折强度影响甚微，纤维含量>3%时效率不高。钢纤维含量为1.5～2.5%，当纤维含量增加时，RPC 的抗压、折性能显着提高；钢纤维掺量由1%增至2%，RPC 抗压强度提升了10.8%，抗折强度则有大幅提升，提升幅度为61%。显然钢纤维对抗折强度的提升作用明显优于其对抗压强度的影响。

图2 为水胶比对RPC 强度的影响曲线，当水胶比介于0.15-0.18 时水胶比对RPC 的抗压、折强度均影响不大；但当水胶比>0.18 时，RPC 的强度开始出现急剧降低。

图3 反应的是沙胶比与RPC 抗压、折预测强度的关系曲线，由图中曲线可以看出砂胶由0.8 上升至1.4，RPC 的抗压强度呈现出先上升后下降的趋势，抗折强度则随着沙胶比的上升而不断降低。

图4 表明，当硅灰掺量介于0.1～0.4 时，RPC 的抗折强度值介于29～32之间，强度值变化不大。当掺量数值介于0.25～0.35 时，其对RPC 的抗压强度有较大幅度的提升，最大提升幅度可达21%，故此范围可作为硅灰掺量的参考取值范围。

5 结论

（1）采用BP 神经网络对RPC 的抗压、折强度进行预测是行之有效的。利用该网络得到的钢纤维掺量、水胶比、硅灰掺量等因素对RPC 强度的影响规律，可为RPC 在工程中的实际配合比提供有效参考。

（2）当钢纤维含量<1%时，其对RPC 强度影响甚微，当大于3%时效率不高，RPC 中钢纤维的合理体积掺量可取为1.5～2.5%。

（3）硅灰对RPC 的抗折强度无显著影响，但其对RPC 立方体抗压强度存在一定程度的提升作用，其参考取值范围可取为0.25～0.35。

（4）水胶比对RPC 的强度有较大影响，当水胶比>0.18 时，RPC 强度出现急剧降低；砂胶比对RPC 强度影响不大。