装配式地下粮仓钢板-混凝土组合仓壁轴压受力性能分析

王振清，侯支龙，张庆章，揣 君

装配式地下粮仓钢板-混凝土组合仓壁轴压受力性能分析

王振清，侯支龙，张庆章※，揣 君

（河南工业大学土木工程学院，郑州 450001）

为了研究装配式地下粮仓钢板-混凝土组合仓壁的轴压力学性能，该研究在仓壁试件轴压试验的基础上，对仓壁试件进行非线性有限元分析，模拟试件加载的全过程，进一步分析试件及其组件在加载过程中的受力性能及工作机理，并对钢板强度、混凝土强度、距厚比等不同的参数影响规律进行了分析。结果表明：有限元模拟结果与试验结果吻合较好，在最大试验载荷5 000 kN时模拟轴向压缩总变形与试验平均轴向压缩总变形相对差值为4.2%，建立的有限元模型适用；在弹性阶段仓壁预制块部位混凝土和接头部位止水钢板分别承担了79.7%和50.9%的荷载，峰值荷载主要由混凝土和传力钢板决定，达到峰值荷载后接头部位止水钢板承担更大的荷载，增强止水钢板可以改善试件的延性；相较钢板强度、距厚比和止水钢板厚度，混凝土强度对仓壁试件的初始刚度和峰值荷载影响最大，混凝土强度、钢板强度、距厚比和止水钢板厚度对峰值荷载回归得到的回归系数值分别为0.910、0.154、−0.005和0.301；止水钢板的强度和厚度较小时，试件易发生脆性破坏；结合设计参数分析中得到的荷载-变形曲线，提出2种荷载-变形模型曲线，进一步提出装配式钢板-混凝土组合仓壁轴压峰值荷载简化计算式，得到的计算峰值荷载与有限元峰值荷载相对差值均不超过9%，计算结果具有较高的精度。研究结果可为装配式地下粮仓仓壁的工程设计提供指导和参考。

仓壁；受力性能；有限元分析；接头；地下粮仓；简化计算

0 引 言

现代地下粮仓（以下简称地下仓）是构建中国绿色生态储粮体系的重要技术支撑[1]。与地上粮仓相比，地下粮仓具有低温减损、绿色环保、节地节能等显著优势，是粮食行业的重要课题之一[2]。近年来，大直径钢筋混凝土地下仓成为现代地下粮仓的典型代表，取得了不少研究成果[3-7]。然而，随着研究工作的不断深入，大直径钢筋混凝土地下仓面临的成本、工期、防水、抗浮等问题逐渐凸显出来。钢筋混凝土地下仓仓壁为现浇成形[8]，现浇钢筋混凝土结构需要有足够的工作面用于支模和搭脚手架，基坑开挖、回填的工程量加大，工期延长。现浇仓壁无法作为基坑支护结构，基坑支护需要另外采取措施。此外，随着基坑开挖深度加大，基坑需要持续降水[9]。基坑开挖、回填、支护、降水费用占地下仓建造成本的比重相当大。同时，地下仓具有高标准的防水要求，钢筋混凝土结构一般采用的卷材防水施工工艺复杂，沿仓壁施工不方便，且卷材易老化，防水性能差。为此，张昊等[10-14]提出了一种在混凝土仓壁内衬聚丙烯塑料板的塑料-混凝土防水体系，并对这种体系的闭水性能、工程承压能力和节点抗拔性能进行了试验研究。但该防水体系尚处于研究阶段，缺乏相应的规范和标准作为支撑，且内衬塑料板仅作为防水层，对混凝土仓壁的结构强度没有增强。当地下仓向高水位等复杂地质条件地区推广，仓体将受到较大的地下水的作用[15]。对于地下仓的抗浮问题，张会军等[15-16]通过建立模型仓，对考虑仓体周围回填二八灰土和砂土等实际工况下的抗浮问题进行了试验研究，但研究成果仅对地下仓的浮力计算提供了建议，并不能解决地下仓面临的抗浮难题。针对以上问题，王振清等[17]提出了一种装配式钢板-混凝土地下粮仓（简称装配式地下仓），该装配式地下仓同时将装配式技术和钢板-混凝土组合结构技术应用其中。采用逆作施工法，避免大开挖，解决了基坑支护难题；钢桩与钢板-混凝土仓壁预制块之间采用干式连接接头，形成整体，缩短施工周期，钢桩可作为抗拔桩，解决了地下湿作业施工周期长和抗浮难题；组合结构内衬单面钢板不仅是结构层，还兼做防水层，解决防水难题。该方案较好地解决了基坑支护、抗浮、防水三大难题，亦可降低建设成本。

这种全新技术体系在地下仓中的直接成果相对较少。国内外学者对隧道衬砌类似工程和钢板-混凝土组合结构进行了大量的研究[18-22]。但装配式地下仓是一种新型结构，其结构形式、受力状态、节点连接方式与现有的钢板-混凝土组合结构或类似工程均不相同。因此，在装配式地下仓结构方案的基础上，结合工程实际，王振清等[23]通过有限元对设计的有、无接头仓壁弹性刚度进行了对比分析，表明设计的接头是安全可靠的，但并未对仓壁及接头进行塑性及承载力分析。在结构设计中，塑性设计可以使结构更加合理且节约材料[24]。该研究在装配式地下仓仓壁试件轴压足尺试验的基础上，采用ABAQUS有限元软件对其进行非线性有限元模拟。分析试件及其组件在加载过程中的受力性能及工作机理，并对影响仓壁设计的参数进行分析，提出的峰值荷载简化计算式，拟为装配式地下仓仓壁的设计提供指导与参考。

1 试验试件及方法

1.1 试件制作

本文装配式地下仓是由仓顶板、仓底板（漏斗状）、仓内筒、组合仓壁和钢桩等组成的地下薄壁圆筒结构，结构方案详见文献[17]。地下仓仓容5×106kg（以小麦计），埋置在地表以下，覆土深约1.5 m，仓内有设备隔层；仓内径25 m，仓壁厚0.31 m，仓底板标高约−21～−28 m，仓壁高约20 m，周围均布36根钢桩。组合仓壁是由预制的单钢板混凝土预制块拼装而成，该预制块内层为钢板，外层为混凝土，两者通过圆柱头栓钉连接为一体。上下预制块间沿仓壁环向的水平接缝为环向接头，左右预制块间沿仓壁高度方向的竖向接缝为竖向接头。由柱壳理论可知，仓壁在外部水土压力作用下，主要为环向受压，沿仓壁高度方向受力较小。根据无接头钢筋混凝土模型计算，仓壁承受的环向最大轴力设计值为4 895 kN。因此，本文主要对组合仓壁及其竖向接头（以下简称仓壁接头）轴压受力性能进行分析。

受试验条件限制，开展地下筒仓组合仓壁整环足尺试验难度较大。缩尺模型存在较大的近似性，由于弧形试件对加载装置要求较高，在保证试件受力状态与工程实际基本相符的前提下，采用平直试件代替实际的弧形试件。进行了2块装配式钢板-混凝土组合仓壁的足尺试验研究，编号分别为SC-N1和SC-N2。试件尺寸及结构如图1所示。各试件尺寸相同，总长度为2 200 mm，宽为1 000 mm，厚310 mm。钢板型号为Q345，混凝土强度等级为C40。仓壁接头细部构造见图1a，仓壁试件采用“喇叭口”空腔形式，由2块U形包边钢板、止水钢板、传力钢板和钢桩翼缘板组成。包边钢板通过栓钉和仓壁混凝土预制在一起，钢桩翼缘板、传力钢板、止水钢板分别与包边钢板采用焊缝连接。

按照设计要求，全部钢构件在钢结构加工厂规范批量加工制作，圆柱头栓钉和钢板用螺柱焊机焊接。各试件的钢构件作为底模，再浇筑混凝土，混凝土养护28 d以上，最后模拟现场施工（立焊）将预制块与钢桩焊接成一体，完成试件的制作。

1.2 试验方法

试验加载设施选用河南省粮油仓储建筑与安全重点实验室电液伺服剪压长柱试验加载系统（YAJ-12000），此试验机能够提供的最大压力为12 000 N。采用轴压的加载方式，加载示意图如图2所示。

根据上文所述的仓壁环向最大轴力设计值，试验最大荷载目标值取为5 000 kN，分25级加载，每级加载速度为2 kN/s。试件的测量数据包含位移和应变，钢板侧和混凝土侧均设置测点，测点布置如图3所示。

试验测量的主要内容包括：试件的轴向压缩总变形、试件不同高度处的压缩变形、钢板和混凝土的应变。试件轴向压缩总变形由底端钢板和混凝土两侧共6个测点（YW1～YW3，YW13～YW15）的位移均值减去顶端6个测点（YW10～YW12，YW22～YW24）位移均值得到。不同高度处压缩变形以每排6个测点的位移均值减去顶端6个测点的位移均值得到。

2 有限元计算模型

2.1 材料的本构模型

1）混凝土采用ABAQUS软件中的塑性损伤模型（Plasticity damage）。该模型中的屈服面采用由Lubline[25]等提出并由Lee和Fenves[26]等在1998年进行修正的准则。混凝土单轴受压和受拉应力-应变关系采用《混凝土结构设计规范》（GB50010-2010）中的模型，弹性模量c为

式中cu为混凝土立方体抗压强度，MPa。

混凝土损伤因子采用Sidoroff[27]提出的计算方法：

式中c为混凝土的应力，MPa；c为混凝土应变。

试验中只对与试件同时浇筑的立方体试块进行了抗压试验，与混凝土本构模型中采用的棱柱体抗压强度c换算关系式为[28]

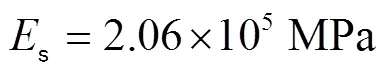
2.2 模型建立

模型中钢板、混凝土和栓钉均采用C3D8R实体单元。栓钉通过Embedded方式嵌入到混凝土中，栓钉与钢板采用刚性连接。通过设置接触单元模拟钢板与混凝土的接触界面，切向方向采用库伦摩擦模型，摩擦系数取0.6，法向方向采用硬接触来模拟。按照试件的实际尺寸建立有限元模型，并采用结构化网格划分技术对每个部件分割成规则的形状。模型的网格密度基本相同，接头处网格加密，根据试算结果，按照此种网格密度进行划分具有较好的计算精度和效率。图4为有限元的几何模型与网格划分。模型中左侧加载端面采用位移的加载方式进行加载，边界条件为左端面所有节点施加向、向位移约束及转动约束，右端面所有节点施加向、向、向位移约束及向、向转动约束。

3 结果与分析

3.1 试验值与有限元计算值对比

由于仓壁试件在试验加载中最大加载值为5 000 kN，取有限元加载到5 000 kN的位移计算结果与试验结果进行对比。图5为荷载与试件的轴向压缩总变形关系曲线。可以看出，试件的试验位移结果与数值模拟位移结果吻合良好，在5 000 kN时尚处于弹性阶段，模拟轴向压缩总变形与试验平均轴向压缩总变形相对差值为4.2%。有限元可以较好的模拟试件的初始刚度。在5 000 kN时试件在不同高度测点的压缩变形如表1所示。可见试件沿试件高度方向没有均匀变形，这是由于实际中试件存在制造误差。但这种影响很小，试验结果与有限元结果相差不大。

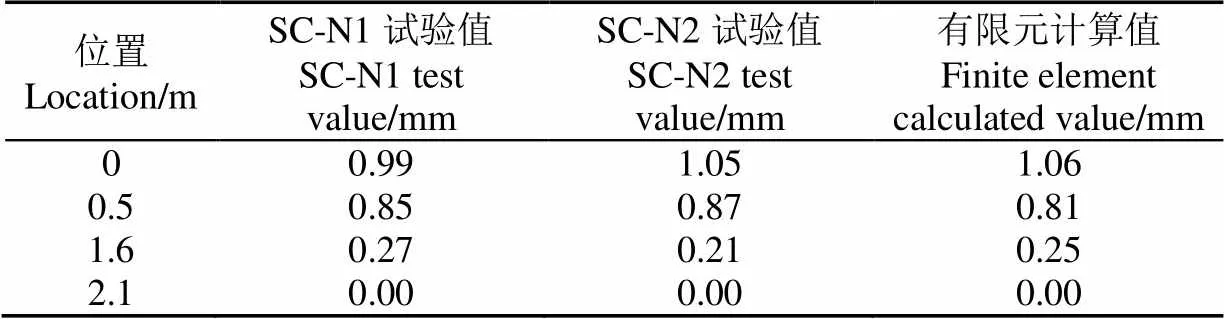
表1 不同高度测点压缩变形

应变对比如图6所示，其中试验值取5 000 kN时2个试件应变平均值。可以看出，模拟值与试验值基本重合，钢板侧和混凝土侧均为压应变，钢板侧的应变分布较为均匀，混凝土侧在靠近接头位置的应变值相对较大。

以上对比分析可知，有限元中采用这种建模方法是有效的，为下文的非线性分析奠定基础。

3.2 仓壁受力机理分析

试件及其组件在加载全过程模拟中的荷载-变形曲线如图7所示。由图7可以看出：1）在弹性阶段（OA段），试件整体及其组件的荷载-变形关系呈线性增长，在A点时各组件与试件整体的荷载比值可以得到各组件承担的相应荷载。预制块内侧钢板和混凝土各自承担20.3%和79.7%的荷载，接头部位钢桩下翼缘、传力钢板和止水钢板承担的荷载分别为19.5%、29.6%和50.9%。可见预制块部位大部分荷载（约80%）由混凝土承担，接头部位大部分荷载（约80%）由传力钢板和止水钢板承担。2）当试件达到峰值荷载时，混凝土和传力钢板承担的荷载也达到峰值，可见试件的峰值荷载主要由混凝土和传力钢板决定。3）当荷载-变形曲线达到B点时，接头位置止水钢板承担着更大的荷载，因此适当增大止水钢板的强度和厚度可在一定程度上增加试件的延性。

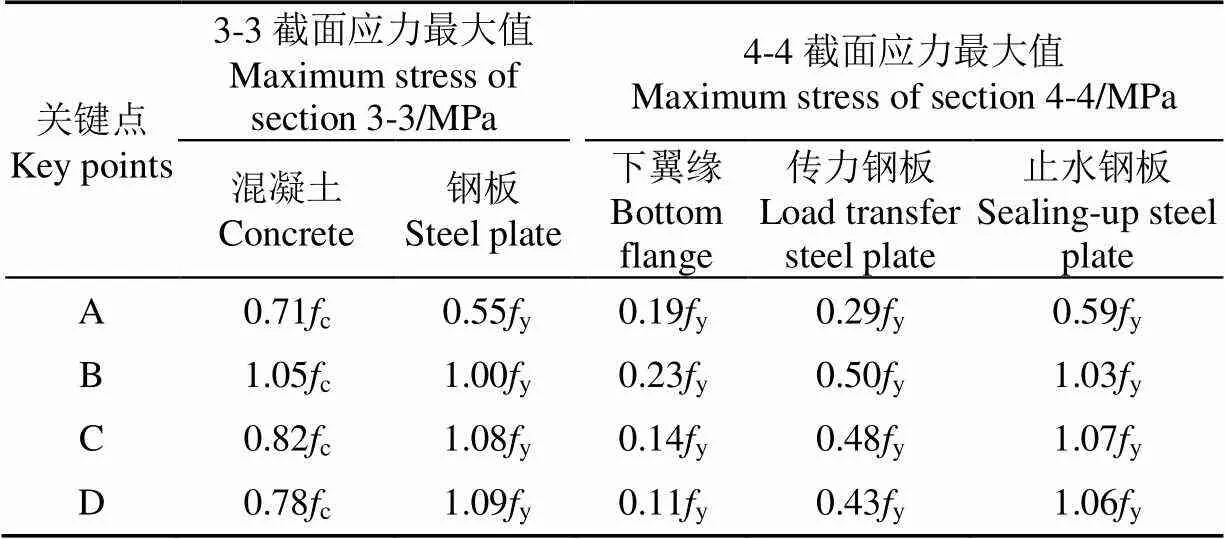
表2 不同截面各组件轴向应力最值

注：c为混凝土棱柱体抗压强度，MPa；y为钢材的屈服应力，MPa。

Note:cis compressive strength of prismatic concrete, MPa;yis yield stress of steel, MPa.

根据钢材的受力发展过程[29]，将试件整体的荷载-变形曲线分成4个阶段：弹性段（OA）、弹塑性段（AB）、塑性段（BC）、硬化段（CD）。表2为试件接头及接头影响范围内不同截面各组件的轴向应力最值。其中，由于钢桩上翼缘和腹板受力较小，跨中截面（4-4截面）只给出了下翼缘、传力钢板和止水钢板的轴向应力在关键点位的应力最值。由图7和表2可知：

1）在OA段，试件各个组件均处于弹性状态，到达A点荷载作用时，3-3截面中混凝土和钢板的最大轴向压应力分别为0.71c和0.55y。4-4截面中钢板的最大轴向压应力为0.59y。由于接头传力钢板和止水钢板的挤压，3-3截面混凝土中相应高度处的轴向应力较大，但这种影响只是局部的。此外，仓壁预制块由单侧钢板组成，中和轴靠近钢板侧，所以4-4截面中3块钢板的轴向应力并不相同，靠近中和轴的钢板所受的应力较大。

2）在AB段，随着荷载的增大，试件及各个组件的轴向应力均有所增大。在峰值荷载（B点）时，3-3截面混凝土中受传力钢板和止水钢板挤压区域轴向应力开始出现不均匀分布，传力钢板挤压区域应力值超过其棱柱体抗压强度，但混凝土大部分截面仍受力较小，处于弹性阶段。接头区域止水钢板开始屈服，跨中止水钢板上表面最大轴向应力达到1.03y。钢桩下翼缘和传力钢板轴向应力增长较小，说明止水钢板为接头的关键受力部位。

3）在BC段，3-3截面混凝土受挤压区域轴向应力进一步不均匀分布，由于发展了较大的轴向应变，受传力钢板挤压的混凝土轴向应力开始下降，传力钢板承担的荷载也不再增加，此时接头位置增加的荷载主要由止水钢板分担。到达C点时，3-3截面钢板和跨中截面止水钢板塑性都进一步发展，最大轴向应力达到了1.08y。

4）随着荷载的继续增大（CD段），荷载-变形曲线进入第二次上升段。这是由于混凝土承担荷载的下降速度(c1)和传力钢板承担荷载的下降速度(sc1)减缓，止水钢板承担荷载的增大速度(sz)和预制块钢板承担荷载的增大速度(s)没有减弱，以BC段相同的速度增大。使试件的承载能力得到了第二次加强。在此阶段，试件下部钢板塑性进一步从中间向两边发展。

3.3 设计参数分析

在试验验证有限元模型参数设置正确性的基础上，建立了13个有限元模型对装配式钢板-混凝土组合仓壁的设计参数进行分析。分析的设计参数包括：混凝土强度、钢板强度、距厚比和止水钢板厚度。表3给出了设计参数的取值及主要结果。以有限元模型PSC-C40为基础模型，各个模型均在基础模型上改变某个参数，其余参数均保持不变。所得各有限元模型的荷载-变形曲线如图8所示。

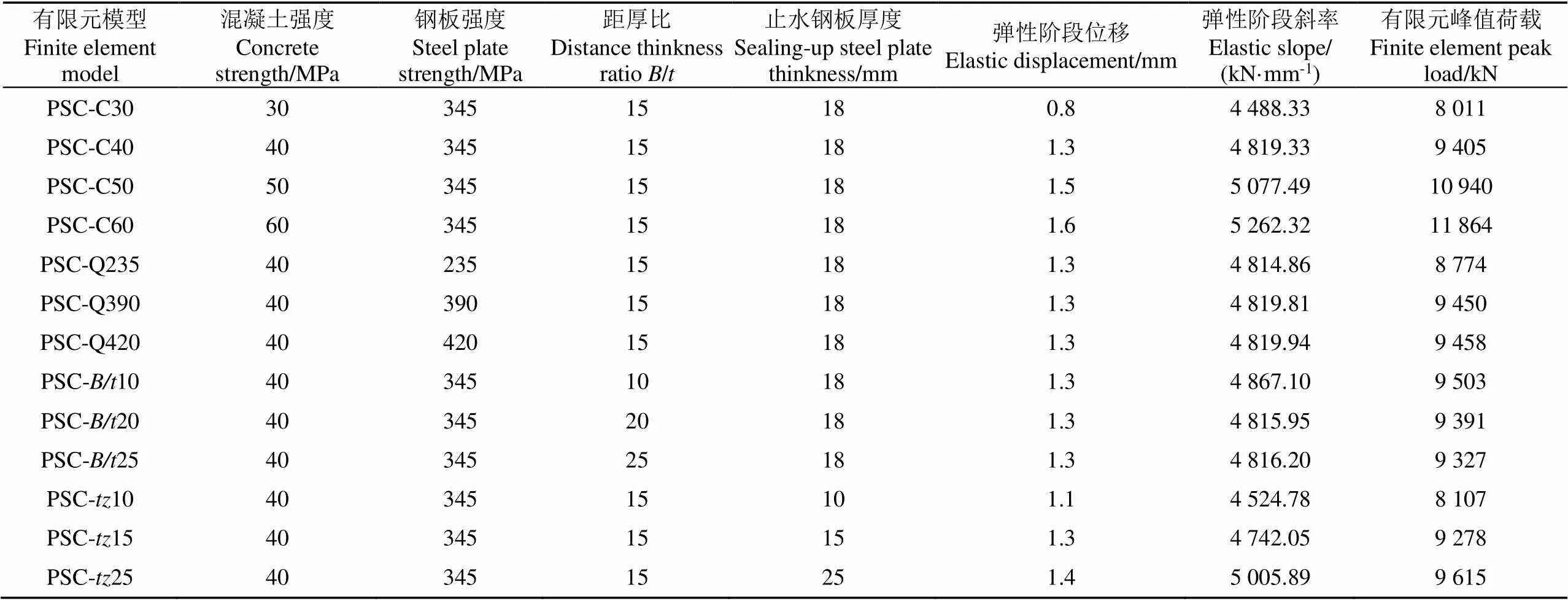
表3 设计参数取值及主要结果

注：表示栓钉轴向（加载方向）间距，表示内侧钢板厚度；PSC-C表示改变混凝土强度的模型；PSC-Q表示改变钢板强度的模型；PSC-表示改变距厚比的模型；PSC-表示改变止水钢板厚度的模型。下同。

Note:/:indicates the axial (loading direction) bolts distance ,indicates the thickness of inner steel plate; PSC-C indicates the model that changes the concrete strength; PSC-Q indicates the model that changes the steel plate strength; PSC-indicates the model that changes the distance thinkness ratio; PSC-indicates the model that changes the sealing-up steel plate thinkness. The same below.

3.3.1 混凝土强度

随着混凝土强度的提高，有限元模型中的弹性阶段位移和刚度依次增大，峰值荷载也明显提高。当混凝土强度从30增大到60 MPa，有限元得到的峰值荷载增幅分别为17.4%、16.3%、8.4%。此外，混凝土强度为30、40和50 MPa时，试件超过峰值荷载后的刚度退化趋势相同。当混凝土强度为60 MPa时，试件超过峰值荷载后的刚度退化较快，承载力下降幅值较大。

3.3.2 钢板强度

随着钢板强度的提高，组合仓壁的弹性阶段刚度和位移变化很小。有限元模型得到的峰值荷载随着钢板强度的提高增幅分别为7.2%、0.5%、0.08%。当钢板强度达到345 MPa，继续增大钢板强度对峰值荷载几乎没有影响。当钢板强度为235 MPa时，试件的承载能力在达到峰值荷载后便逐渐减小，这是由于接头处止水钢板在峰值荷载时几乎完全进入屈服（图8b应力云图），不能继续承担荷载。钢板强度为345、390和420 MPa时，试件的荷载-变形曲线区别很小，只在第二次上升段有微小变化，且承载能力随着钢板强度的提高而提高。可见，当钢板达到一定强度后，提高钢板强度对增强试件的峰值荷载效果较弱，但可以一定程度上增加试件在达到峰值荷载后的承载能力。从受力机理分析中可知，峰值荷载后仓壁组件只有止水钢板和内侧钢板承载能力继续增大，因此增大钢板强度可以提高荷载峰值后的承载能力。

3.3.3 距厚比

距厚比是通过改变栓钉轴向间距来实现。有限元模型中钢板-混凝土组合仓壁的距厚比对其初始刚度、变形能力和峰值荷载影响很小。当试件处于弹性阶段以及弹塑性阶段时，不同距厚比试件的荷载-变形曲线基本重合。当试件进入塑性阶段后，随着距厚比的增大，试件的承载能力逐渐减弱。这是由于当距厚比较大时，内侧钢板和混凝土的约束变弱。内侧钢板因承担的荷载逐渐增大而发生局部屈曲，从而使试件的承载力下降。

3.3.4 止水钢板厚度

随着止水钢板厚度的增大，试件的峰值荷载增幅分别为4.8%、1.6%和3.8%，增幅相对较弱。当钢板厚度为10 mm时，荷载-变形曲线没有硬化段，原因同PSC-Q235。此时止水钢板在达到峰值荷载时已完全进入屈服阶段（图8d应力云图），丧失了承载能力。因为硬化阶段止水钢板对试件的承载能力起主要作用，钢板厚度为15、18、25 mm时，其硬化程度依次增强。

3.4 参数敏感性分析

以峰值荷载作为因变量，将混凝土强度、钢板强度、距厚比和止水钢板厚度作为自变量进行多元线性回归分析，得到的回归参数如表4所示。

从表4可以看出，参数混凝土强度、钢板强度、距厚比和止水钢板厚度的Beta值分别为0.910、0.154、−0.005和0.301，说明混凝土强度对组合仓壁峰值荷载的影响最大，止水钢板厚度对峰值荷载的影响次之，钢板强度和距厚比对峰值荷载的影响较弱。由显著性可知混凝土强度和止水钢板厚度显著，钢板强度和距厚比不显著，在荷载设计值的基础上，应主要提高混凝土强度和止水钢板厚度以提高组合仓壁的承载能力。

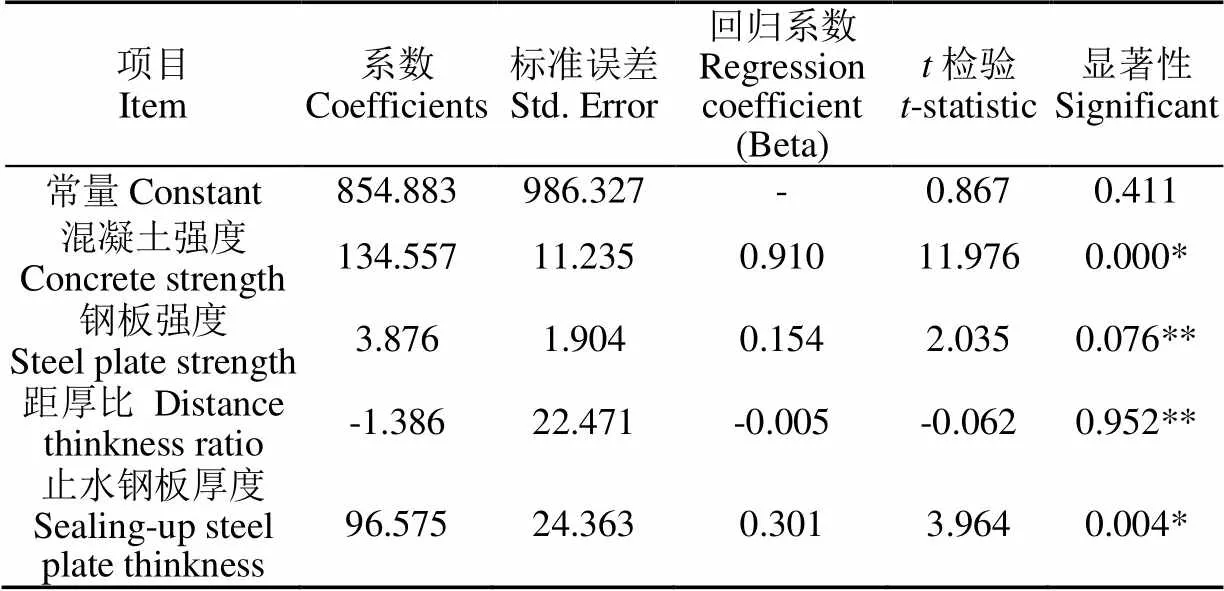
表4 回归参数

注：在0.05的显著性水平下，*表示显著，**表示不显著

Note: At the significance level of 0.05, * indicates significant, and ** indicates not significant.

4 承载力分析

由设计参数分析可知，除有限元模型PSC-Q235和PSC-10的荷载-变形曲线只经历了弹性段、弹塑性段和塑性段，其余有限元模型的荷载-变形曲线均经历了弹性段、弹塑性段、塑性段和硬化段。将以上2种荷载-变形曲线模型化，如图9所示。其中，有限元模型PSC-Q235和PSC-10的荷载-变形曲线可简化为ML-2，其余有限元模型的荷载-变形曲线可简化为ML-1。

在模型化荷载-变形曲线ML-1中，仓壁试件达到峰值荷载时，混凝土和传力钢板承担的荷载均达到峰值，仓壁其余组件仍可继续承担荷载（见图7）。此时受挤压混凝土最大轴向应力为1.05c，传力钢板最大轴向应力为0.50y。可见，um由受挤压混凝土决定，根据混凝土受压承载力计算公式[30]，um可按下式计算：

式中c表示传力钢板对轴力的贡献系数；um表示ML-1峰值荷载，N；c表示传力钢板受到的轴力，N；c表示受传力钢板挤压的混凝土截面面积，mm2。

对于模型化荷载-变形曲线ML-2，由于接头截面中止水钢板承担的荷载较大，当止水钢板的强度和厚度较弱时，止水钢板会先于受挤压混凝土达到极限抗压强度而屈服。此时，u由止水钢板决定，计算公式如下：

式中z表示止水钢板对轴力的贡献系数；u表示ML-2峰值荷载，N；z表示止水钢板受到的轴力，N；z表示止水钢板的截面面积，mm2。

采用以上模型化方法对装配式钢板-混凝土组合仓壁试件的峰值荷载计算结果如表5，与有限元结果对比分析可知，两者相对差值不超过9%，本文提出的方法可以较为合理的估算装配式钢板-混凝土组合仓壁试件的峰值承载力，为装配式地下仓仓壁的工程设计提供指导与参考。

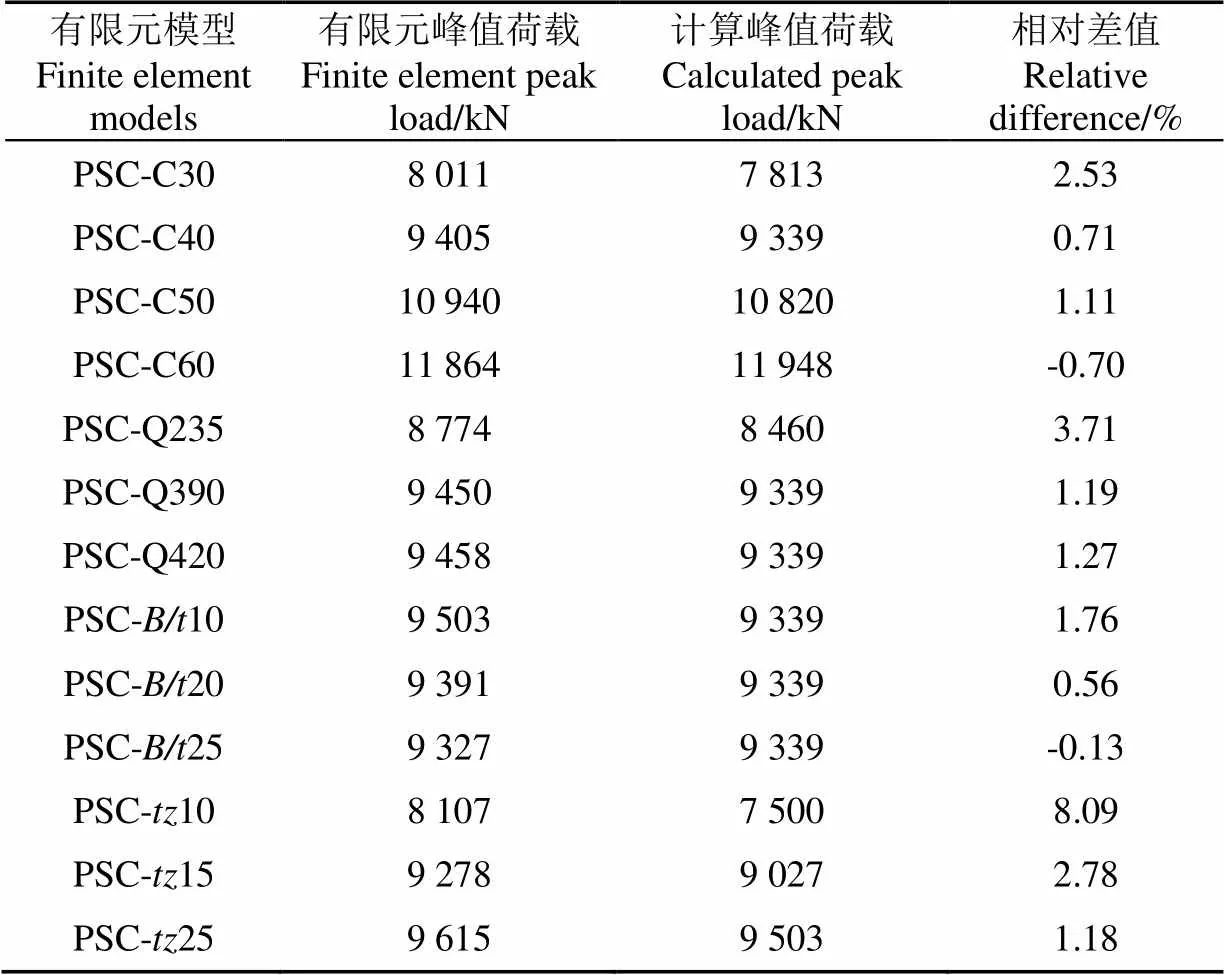
表5 计算峰值荷载

5 结 论

本文根据试验结果，对装配式钢板-混凝土组合仓壁进行了有限元分析。分析结果与试验结果吻合较好，最大试验载荷5 000 kN时模拟轴向压缩总变形与试验平均轴向压缩总变形相对差值为4.2%，表明有限元模型设置合理。进而基于有限元模型开展了机理分析和参数分析，主要得到以下结论：

1）在弹性阶段预制块混凝土和接头止水钢板承担了大部分荷载，混凝土承担的荷载为79.7%，止水钢板承担的荷载为50.9%。止水钢板在试件进入塑性阶段后发挥主要作用，增强止水钢板可以改善试件的延性。

2）相较钢板强度、距厚比和止水钢板厚度，混凝土强度对试件初始刚度和峰值荷载的影响更为显著。混凝土对峰值荷载的回归系数为0.910，钢板强度、距厚比和止水钢板厚度对峰值荷载的回归系数分别为0.154、−0.005和0.301。

3）试件设计时应保证止水钢板的强度和厚度，若止水钢板较弱，峰值荷载较低且易发生脆性破坏。

4）建议了装配式钢板-混凝土组合仓壁峰值荷载简化计算式，得到的计算峰值荷载与有限元峰值荷载相对差值不超过9%，简化计算式具有较高的精度。

[1]王振清. 粮仓建筑基本理论与设计[M]. 郑州：河南科学技术出版社，2015.

[2]郑培，王振清，余汉华. 我国地下仓的简史及特点[J]. 粮油加工，2009(1)：90-94. Zheng Pei, Wang Zhenqing, Yu Hanhua. Brief history and characteristic of underground warehouse in china[J]. Cereals and Oils Processing. 2009(1): 90-94. (in Chinese with English abstract)

[3]熊晓莉，金立兵，王振清. 钢筋混凝土地下粮仓仓壁土压力取值方法及仓壁结构受力分析[J]. 应用基础与工程科学学报，2016(1)：103-114. Xiong Xiaoli, Jin Libing, Wang Zhenqing. Earth pressure and bearing capacity analysis on the wall of reinforced concrete underground granary[J]. Journal of Basic Science and Engineering. 2016(1): 103-114. (in Chinese with English abstract)

[4]金立兵，刘斐骁，田栋杰. 地下钢筋砼筒仓施工与闭水试验过程的抗浮试验研究[J]. 河南工业大学学报：自然科学版，2017，38(2)：105-108，128. Jin Libing, Liu Feixiao, Tian Dongjie. Anti-floating test in construction and closed-water test process of underground reinforced concrete silos[J]. Journal of Henan University of Technology: Natural Science Edition, 2017, 38(2): 105-108, 128. (in Chinese with English abstract)

[5]金立兵，梁新亚，霍承鼎，等. 地下混凝土筒仓仓壁力学性能工程试验与数值分析[J]. 土木与环境工程学报（中英文），2020，42(3)：40-45. Jin Libing, Liang Xinya, Huo Chengding, et al. Engineering test and numerical analysis of underground concrete silo[J]. Journal of Civil and Environmental Engineering (Chinese and English), 2020, 42(3): 40-45. (in Chinese with English abstract)

[6]陈桂香，崔晨星，付志永，等. 钢筋混凝土地下粮食筒仓受力监测分析[J]. 河南工业大学学报：自然科学版，2016，37(6)：90-95. Chen Guixiang, Cui Chenxing, Fu Zhiyong, et al. Monitoring analysis on the stress of reinforced concrete underground grain silo[J]. Journal of Henan University of Technology: Natural Science Edition, 2016, 37(6): 90-95. (in Chinese with English abstract)

[7]熊晓莉，金立兵，史笑珂，等. 钢筋混凝土圆形地下粮仓仓壁承载力计算方法研究[J]. 河南工业大学学报：自然科学版，2015，36(1)：95-99. Xiong Xiaoli, Jin Libing, Shi Xiaoke, et al. Study on wall bearing capacity calculation method of reinforced concrete underground granary[J]. Journal of Henan University of Technology: Natural Science Edition, 2015, 36(1): 95-99. (in Chinese with English abstract)

[8]周春雷. 地下大直径钢筋砼圆形粮仓倒锥形仓底板受力性能研究[D]. 郑州：河南工业大学，2013. Zhou Chunlei. Study on Mechanical Behavior of invert tapered Shell bottom board structure for Large-Diameter Reinforced Concrete Underground Silo[D]. Zhengzhou: Henan University of Technology, 2003. (in Chinese with English abstract)

[9]贾腾南. 基于空间受力的地下钢筋混凝土粮食筒仓仓壁受力分析[D]. 郑州：河南工业大学，2014. Jia Tengnan. Wall Stress Analysis of Reinforced Concrete Underground Granary Based on the Space Stress[D]. Zhengzhou: Henan University of Technology, 2014. (in Chinese with English abstract)

[10]张昊，席晗，陶元庆. 内衬塑料防水板水压力作用下的受力性能分析[J]. 新型建筑材料，2020，47(4)：157-160. Zhang Hao, Xi Han, Tao Yuanqing. Analysis of mechanical properties under water pressure of lined plastic waterproof board[J]. New Building Materials, 2020, 47(4): 157-160. (in Chinese with English abstract)

[11]席晗，韩露，曹瑞峰，等. 塑料防水板节点连接强度的水压试验研究[J]. 新型建筑料，2020，47(12)：122-125，139. Xi Han, Han Lu, Cao Ruifeng, et al. Hydrostatic test of plastic waterproof board based on joint strength[J]. New Building Materials, 2020, 47(12): 122-125, 139. (in Chinese with English abstract)

[12]尹淑君，王振清，张昊. 聚丙烯塑料棒在混凝土中的抗拔性能有限元分析[J]. 四川建筑科学研究，2019，45(2)：75-77.Yin Shujun, Wang Zhenqing, Zhang Hao. FEA on pullout performance of PP bar in concrete structure[J]. Sichuan Building Science, 2019, 45(2): 75-77. (in Chinese with English abstract)

[13]王振清，常哲，张昊，等. 聚丙烯棒在混凝土中的黏结性能试验研究[J]. 科学技术与工程，2020，20(22)：9170-9175. Wang Zhenqing, Chang Zhe, Zhang Hao, et al. Experimental study on bonding property of polypropylene bar in concrete[J]. Science Technology and Engineering, 2020, 20(22): 9170-9175. (in Chinese with English abstract)

[14]张昊，席晗，李凯，等. 聚丙烯塑料螺纹焊接节点轴心拉力试验研究[J]. 河南科技，2019(23)：112-113. Zhang Hao, Xi Han, Li Kai, et al. Research on axial tension test of polypropylene plastic thread welded joints[J]. Journal of Henan Science and Technology, 2019(23): 112-113. (in Chinese with English abstract)

[15]张会军，刘海燕，张庆章. 砂土中地下粮食圆形筒仓抗浮模拟实验研究[J]. 粮油食品科技，2017，25(2)：99-104. Zhang Huijun, Liu Haiyan , Zhang Qingzhang. Simulation experiment of anti-floating of underground grain silos in sandy soil[J]. Science and Technology of Cereals, Oils and Foods, 2017, 25(2): 99-104. (in Chinese with English abstract)

[16]刘海燕，孟伟新，王振清，等. “二八灰土”回填地下粮仓浮力预警试验研究[J]. 农业工程学报，2019，35(11)：299-305. Liu Haiyan, Meng Weixin, Wang Zhenqing, et al. Buoyancy early warning of underground granary with “2:8 lime soil” backfilling[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(11): 299-305. (in Chinese with English abstract)

[17]王振清，揣君，刘永超，等. 地下粮仓的结构设计研究现状与新进展[J]. 河南工业大学学报：自然科学版，2019，40(5)：132-138. Wang Zhenqing, Chuai Jun, Liu Yongchao, et al. Current situation and new progress of structural design of underground silos[J]. Journal of Henan University of Technology: Natural Science Edition, 2019, 40(5): 132-138. (in Chinese with English abstract)

[18]Lu L, Lu X, Fan P. Full-ring experimental study of the lining structure of shanghai changjiang tunnel[J]. Journal of Civil Engineering and Architecture, 2011, 5(8): 732-739.

[19]闫治国，丁文其，沈碧伟，等. 输水盾构隧道管片接头力学与变形模型研究[J]. 岩土工程学报，2011，33(8)：1185-1191. Yan Zhiguo, Ding Wenqi, Shen Biwei, et al. Structural model for radial joints of water-conveyance shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(8): 1185-1191. (in Chinese with English abstract)

[20]张有佳，李小军. 钢板混凝土组合墙轴压受力性能有限元分析[J]. 工程力学，2016，33(8)：84-92. Zhang Youjia, Li Xiaojun. Finite element analysis of axial compreesive stress performance for steel plate reinforced concrete compound walls[J]. Engineering Mechanics, 2015, 23(6): 1198-1209. (in Chinese with English abstract)

[21]Liang Q Q, Brian U, Howard D W, et al. Local buckling of steel plates in double skin composite panels under biaxial compression and shear[J]. Journal of Structural Engineering, 2004, 130(3): 443-451.

[22]赵洁，聂建国. 钢板-混凝土组合梁的非线性有限元分析[J]. 工程力学，2009，26(4)：105-112. Zhao Jie, Nie Jianguo. Nonlinear finite element analysis of steel plate-concrete composite beams[J]. Engineering Mechanics, 2009, 26(4): 105-112. (in Chinese with English abstract)

[23]王振清，揣君，王录民，等. 装配式地下粮仓钢-混组合仓壁节点力学性能有限元分析[J]. 农业工程学报，2019，35(24)：298-306，327. Wang Zhenqing, Chuai Jun, Wang Lumin, et al. Finite element analysis on mechanical properties of joint in precast steel plate-concrete composite wall of underground granary[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(24): 298-306, 327. (in Chinese with English abstract)

[24]GB/T 50017-2003钢结构设计规范[S]. 北京：中国计划出版社，2013.

[25]Lubliner J, Olive J, Oller S, et al. A plastic-damage model for concrete[J]. International Journal of Solids and Structures, 1989, 25(3): 299-326.

[26]Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900.

[27]Sidoroff F. Description of anisotropic damage application to elasticity[J]. Physical Non-Linearities in Structural Analysis, 1981, 237-244.

[28]赵洁，聂建国. 钢板-混凝土组合加固钢筋混凝土梁的非线性有限元分析[J]. 计算力学学报，2009，26(6)：906-912. Zhao Jie, Nie Jianguo. Nonlinear finite element analysis of RC beams strengthened using steel plate-concrete composite technique[J]. Chinese Journal of Computational Mechanics, 2009, 26(6): 906-912. (in Chinese with English abstract)

[29]陈绍蕃，顾强. 钢结构基础[M]. 北京：中国建筑工业出版社，2014.

[30]陈宗平，薛建阳，刘义，等. 混凝土结构设计原理[M]. 北京：中国电力出版社，2010.

Performance analysis of axial compressive behavior for precast steel plate-concrete composite silo wall of underground silo

Wang Zhenqing, Hou Zhilong, Zhang Qingzhang※, Chuai Jun

(,,450001,)

An underground silo is essential to green grain storage, due to its low temperature, low land consumption, energy conservation, and environmental protection. A new underground silo was proposed in combination with the prefabricated technology and combined structure technology in the engineering practice. In this study, a finite element model of steel plate-concrete composite silo wall containing stud was established on the ABAQUS software, in order to explore the compressive properties of assembled underground silo using the full-scale axial compression test. A nonlinear finite element model of silo wall specimen was also established, concurrently considering the plastic damage of concrete and the elastoplasticity of steel plate. A simulation was performed on the whole loading process of specimens, thereby to analyze the mechanical properties and working mechanism. Various parameters were determined, such as the steel plate strength, concrete strength, and distance thickness ratio. The results showed that: The finite element simulation was in good agreement with the test. Moreover, the relative difference of axial deformation between the simulated and experimental value was 4.2% at 5 000 kN, indicating an applicable finite element model. The precast block concrete and the joint sealing-up steel plate could bear the load of 79.7%, and 50.9%, respectively, during the elastic stage. The peak load depended mainly on the precast concrete of silo wall and the load transfer of steel plates. There was more load in the sealing-up steel plate at the joint position after reaching the peak load. As such, strengthening the sealing-up steel plate can be used to improve the ductility of the specimen. There was the greatest influence of concrete strength on the initial stiffness and the ultimate bearing capacity of specimens, compared with the strength of steel plate, the distance thickness ratio, and sealing-up steel plate thickness. The regression coefficient of concrete strength, steel plate strength, distance thickness ratio, and sealing-up steel plate thickness to peak load were 0.910, 0.154, -0.005, and 0.301, respectively. The specimens were prone to brittle failure, due to the small strength and thickness of sealing-up steel plate. Two curves of load-deformation model were proposed in combination with the load-deformation curves for the silo wall specimens with the assembled steel plate-concrete composite under the various parameters. Furthermore, the simplified formula was also proposed for the axial peak load of the assembled steel plate-concrete composite silo wall. The relative difference of peak loads obtained by the calculation formula and the finite element method was not more than 9%, indicating high accuracy of calculation. The research findings can provide potential guidance for the engineering design of prefabricated underground silo wall.

silo wall; mechanical performance; finite element analysis; joint; underground silo; simplified calculation

王振清，侯支龙，张庆章，等. 装配式地下粮仓钢板-混凝土组合仓壁轴压受力性能分析[J]. 农业工程学报，2021，37(1)：59-67.doi：10.11975/j.issn.1002-6819.2021.01.008 http://www.tcsae.org

Wang Zhenqing, Hou Zhilong, Zhang Qingzhang, et al. Performance analysis of axial compressive behavior for precast steel plate-concrete composite silo wall of underground silo[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(1): 59-67. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.01.008 http://www.tcsae.org

2020-10-20

2020-12-10

国家自然科学基金项目（51509084）；河南省重点研发与推广专项（科技攻关）项目（192102310278）；河南省高等学校青年骨干教师培养计划（2019GGJS086）；河南工业大学青年骨干教师培养计划

王振清，教授，博士生导师，主要研究方向为储仓结构和绿色储粮体系。Email：hnzzwzhq@163.com

张庆章，副教授，主要研究方向为地下粮仓设计。Email：zqz313@163.com

10.11975/j.issn.1002-6819.2021.01.008

TU267+.1

A

1002-6819(2021)-01-0059-09