不同掌子面间距下浅埋偏压小净距隧道稳定性研究

赵阳 徐东强

摘要 浅埋偏压小净距隧道结构特殊，两主洞同时施工时掌子面间距的合理选择对隧道稳定性尤为重要。以延崇高速公路头炮隧道为背景，通过ANSYS及FLAC3D软件建立隧道模型并进行数值模拟，采用了双侧壁导坑法先开挖深埋侧隧道的基础上，将规范中建议的小净距隧道施工时掌子面间距为1～2倍洞径的范围细化为4种不同工况，从隧道上部边坡位移、围岩位移及应力、初衬变形及应力、塑性区体积及锚杆受力等方面进行隧道稳定性的分析，最终得到两主洞掌子面保持2倍洞径时施工隧道稳定性最好，可为本工程及相似工程提供参考。

关 键 词 浅埋偏压小净距隧道;数值模拟;掌子面间距;稳定性

中图分类号 U451     文献标志码 A

Abstract Due to the special structure of shallow buried bias tunnel with small span， it is particularly important for the stability of the tunnel to choose reasonable distance of tunnel faces when two main tunnels constructing at the same time. Based on TouPao tunnel on YanQing-ChongLi highway， use ANSYS and FLAC3D to establish the model and take numerical simulation after make sure the tunnel uses both side heading method and deep buried side excavates first， put the distance that 1～2 times of hole diameter range between two tunnel faces of excavation of shallow buried bias tunnel with small span which the standard suggested into 4 situations， analyze the stability of tunnel from displacement of upper slope， displacement and stress of surrounding rock and tunnel lining， volume of plastic zone and stress of bolts， finally it is best for the stability of tunnel to choose 2 times of hole diameter.

Key words shallow buried bias tunnel with small span; numerical simulation; distance of tunnel faces; stability

0 引言

我国经济不断发展，城市建设不断推进，公路、铁路里程数与日俱增，地下工程项目也越来越多。随着交通线路的不断外延扩展，山区地质情况也越来越复杂。因地形、地质或施工等因素的影响，使得隧道线路无法与等高线垂直时，需在靠近边坡且埋深较浅的位置修建隧道，顶部由于地形原因会产生偏壓，此时若隧道两主洞距离小于一定范围，便形成了浅埋偏压小净距隧道。

许多学者对这一形式隧道的相关稳定性进行了研究：张运良等[1]运用ANSYS有限元程序，研究了浅埋偏压小净距隧道在不同偏压角度、间距、埋深条件下，先开挖深埋侧和先开挖浅埋侧2种不同的开挖顺序下的受力和变形特性，得到了不同间距对应不同开挖顺序的合理开挖方案;苗天[2]对非对称结构偏压小净距隧道采用三台阶法、CRD法和双侧壁导坑法，左右洞分别先行共6种工法进行数值模拟，得到不同施工方法及不同开挖顺序下隧道稳定性变化的相关结论，并对隧道开挖施工提出了建议;腾俊洋等[3]根据浅埋偏压小净距隧道受力特点，分析了考虑不同地形坡度及埋深2种工况下围岩破裂范围、水平侧应力、拱顶压力的影响规律，推导得出了考虑施工工序及地形坡度的浅埋偏压小净距隧道围岩压力计算公式;Chapman等 [4]对伦敦地层中的小净距隧道施工过程进行了二维模拟，重点研究了开挖步骤对地表沉降的影响规律;Do等[5]采用FLAC3D对隧道所受影响进行了预测，在此基础上模拟了隧道施工过程的大部分要素。研究了掌子面间距对隧道结构受力及上部地表位移的影响;Tiwani等[6]利用三维非线性有限元法对并行隧道爆破相互影响进行了研究，认为隧道开挖爆破时的装药量和施工时双洞掌子面间距是隧道支护结构以及围岩的变形和破坏的主要影响因素。Paternest等[7]依托某浅埋小净距隧道实际工程优化了隧道施工中支护结构的支护参数。

本文以延崇高速公路头炮隧道为背景，该隧道为浅埋偏压小净距形式，运用ANSYS及FLAC3D软件建立了隧道采用双侧壁导坑法先开挖深埋侧，且两主洞掌子面间距分别为12 m、16 m、20 m和24 m下的4种工况模型，对隧道在上部边坡位移、围岩位移及应力、初衬变形及应力、塑性区体积及锚杆受力等方面进行稳定性分析，得到掌子面间距为24 m（2倍洞径）时隧道施工稳定性最好，可以为相似工程提供参考。

1 隧道浅埋偏压及小净距判定

1.1 隧道浅埋的判定

深埋隧道可利用围岩自身承载特性形成稳定压力拱，同时结合新奥法下的支护体系共同承载围岩压力，而浅埋隧道无法形成稳定的压力拱，又容易受到不同地表情况的影响，要根据具体情况对设置支护措施。《公路隧道设计规范》（JTG D70—2004）[8]中提供了依据荷载等效高度、地质条件、施工方法等因素判定隧道浅埋与深埋的方法。见式（1），当埋深大于下值时为深埋隧道，否则为浅埋隧道：

1.2 隧道偏压的判定

隧道偏压主要分为地形引起的偏压、地质因素引起的偏压、施工原因引起的偏压3种情况。隧道上部覆土厚度较薄时，地表存在明显倾斜并且岩体较破碎松散，即为地形产生的偏压，常见于边坡浅埋和洞口地段;当岩层存在倾斜的层状结构，层理间的粘结力差并伴随裂隙发育或围岩存在软弱结构面且倾角较大，即产生地质构造引起的偏压;若隧道在施工期间因施工方式不合理便会产生由施工引起的偏压。

图1中a）为地形引起的偏压，其中1∶n为地表边坡与水平面夹角的正切值，t表示偏压侧隧道外侧拱肩到偏压地表的垂直距离，如果t小于表1中的对应值，则将隧道视为地形偏压下的隧道。

1.3 小净距隧道

小净距是指隧道两主洞之间的中夹岩柱厚度小于隧道洞径一定倍数值，倍数的取值对应着不同的隧道围岩级别，整体在1. 0到4. 0之间[8]，表2为《公路隧道设计规范》（JTG D70—2004）中给出的分离式隧道与小净距隧道在不同围岩级别下的区分界限。

2 工程概况及数值模型建立

重庆交通科研设计院等单位编制了《小净距隧道设计施工细则》，其中对Ⅴ、Ⅵ级围岩建议选用单或双侧壁导坑施工方法;施工时两主洞掌子面建议保持在1～2倍洞径的距离，依据规范建议的数值将头炮隧道掌子面间距分为12 m、16 m、20 m及24 m这4种工况进行模拟分析。

2.1 工程概況

延庆至崇礼高速公路头炮隧道位于赤城县大海陀乡头炮村南，洞径12. 098 m，两主洞间距26. 64 m，属小净距隧道，隧道左幅ZK33+550～ZK33+922，长372 m，隧道右幅K33+524～K33+910，长386 m，属短隧道，隧道最大埋深约为79 m，灯光照明，自然通风。

隧道浅埋侧上部地表边坡与水平面夹角正切值为1∶1.2，偏压侧外拱肩到偏压地表垂直距离3.5 m，洞口段为Ⅴ级围岩且进洞口处岩体较破碎，地形偏压作用明显。左幅为浅埋侧隧道，埋深5 m左右，右幅为深埋侧隧道，埋深15 m左右;左幅隧道上部边坡倾角25°左右，右幅隧道上部边坡倾角10°左右，隧道上部偏压边坡倾角在两隧道中部发生改变，沿深埋侧隧道倾角变缓，具体情况见图2。

2.2 数值模型建立

隧道的内轮廓采用五心圆形式，如图3所示。

利用前处理功能较好的ANSYS建立隧道洞身模型，划分网格后导入到FLAC3D中完成完整模型的建立，为使隧道开挖引起的边界位移可忽略不计，左右边界围岩范围取为5倍洞跨，隧道断面的下边缘到围岩下边界的距离取为隧道开挖高度的5倍[9-13]，具体见图4。

2.3 本构模型及参数选取

依据实际工程中的资料，结合文献中常用的经验参数，本次数值模拟模型的本构模型及参数选取情况见表3，模型纵向长度为30 m，开挖进尺定为2 m，同时每开挖2 m进深立即施作初期支护，使初期支护紧跟工作面，相关测点布置如图5～图7所示。

隧道开挖模拟示意图见图8。

2.4 模拟结果与实际量测对比

隧道实际施工采取双侧壁导坑法深埋侧隧道先开挖的方式，两洞掌子面间隔1倍洞径，选取同样的施工方案进行模拟，监控点位选取深埋侧隧道开挖面拱顶处，记录沉降量随开挖面推进的变化，与实际开挖中开挖面拱顶沉降量测曲线对比如图9。

由图9可以看出，实际施工时隧道拱顶的沉降值整体均大于模拟值，因在模拟过程中对隧道外部环境构造和施工过程进行了一定程度的简化，且未考虑岩体中的节理裂隙、渗流作用、构造应力等，这些因素均会对开挖时隧道的变形产生影响;从沉降值变化趋势来看，前期随开挖面的推进，沉降量增大，到达接近所设距离一半的时候，拱顶沉降值的增加速度变小，在开挖进尺达到22 m左右的时候，沉降量基本不变，变化情况基本符合工程情况。

3 隧道稳定性分析

3.1 上部边坡位移分析

4种工况对应隧道模型开挖完成后，上部边坡竖向及水平位移曲线图见图10及图11。

由图10可知，4种不同工况下的模型竖向位移差别不大，上部边坡坡脚处的跟踪点1和跟踪点2由于边坡偏压的关系产生了向上的拱起，但其沉降的发展趋势随着点位的移动变化明显，跟踪点位向右移动时，竖向位移很快进入了沉降阶段;从跟踪点3即浅埋侧隧道的拱顶位置开始，竖向沉降值增加但增加的速率变小，到达深埋侧隧道附近时，因其埋深较深，在拱顶位置出现了竖向沉降最大值，远离了拱顶位置后，沉降值变小，模型4的整体竖向沉降值最小。

由图11可知，隧道上部边坡水平位移值在隧道跨度范围内，随边坡高度的增加而增加;中夹岩柱上方地表远离了隧道开挖范围并且偏压边坡角度变缓，水平位移值开始显著减小;跟踪点4～6与跟踪点7～9相比可以看出，坡度的变缓导致了水平位移减小程度也变缓;4组模型水平位移值相差不大，模型4对于水平位移的控制效果最好。综上所述，模型4对上部地表的竖向沉降和水平位移的控制效果最好。

3.2 隧道围岩位移及受力分析

4种工况开挖完成后，隧道围岩竖向及水平位移云图如图12及图13，开挖结束后隧道竖向及水平最大位移值见表4。

由图12及图13可见，4个模型的竖向位移云图和水平位移云图大体一致。

竖向位移方面，都表现为深埋侧隧道竖向沉降与拱底拱起最大，又因为上部边坡偏压关系，顺偏压方向有所倾斜，使得沉降最大值出现部位向右拱肩方向移动;浅埋侧隧道边坡坡脚处左侧都出现了明显的向上拱起现象，是由于上部偏压边坡的存在且坡脚处覆土厚度较薄，拱底拱起影响到左侧部分，施工中要注意此处的监控，必要时进行反压回填、边坡卸载、设置挡土墙等措施，保证隧道稳定。

水平位移方面，由于浅埋侧隧道位于偏压边坡坡脚，偏压影响最严重，水平位移产生了最大值，位于拱肩处，也符合偏压的方向分布，施工中要注意此处的水平位移变化，及时进行防护;水平位移对深埋侧隧道的影响范围较大，包含了上部地表、右拱脚及其下侧还有浅埋侧隧道部分，施工监控量测中要将两主洞位移情况互相联系。4种工况下隧道竖向与水平位移统计见表4。

从表4中可以看出，隧道开挖完成后拱顶沉降值和拱底拱起值随掌子面间距的增大而减小，增加的趋势逐渐变缓，趋于稳定，模型1～3的水平位移随掌子面间距增大而增大，而模型4的水平位移又减小到和模型1相似。

综上所述，两主洞开挖掌子面间距选取24 m（2倍洞径）对隧道竖向及水平位移稳定最有利。

对图14与图15进行分析可知，两侧隧道的竖向应力最大值均出现在拱腰、拱脚部位，4组模型左、右幅隧道拱顶与拱底竖向应力值相差不大;浅埋侧隧道受偏压严重，竖向应力最大值出现在其右拱腰和右拱脚处，明显大于对称侧的左拱腰和左拱脚，深埋侧隧道拱腰与拱脚左右应力值相差不大。综合来看，选取模型4对于隧道开挖时竖向应力的控制效果最好。

3.3 初期衬砌位移及受力分析

表5为初期衬砌位移及受力统计表。由表5可以看出，模型1应力值与位移值均最大，对初衬稳定性不利，模型4的拱顶沉降与水平位移最小，竖向应力最大，水平应力也较大，在提供了较大支护抗力减少二衬受力的同时能够减小支护结构的位移。综合来看，施工时掌子面间距采取24 m（2倍洞径）进行施工，初衬的稳定性效果最好，对隧道整体的稳定性也最好。

3.4 隧道塑性区分析

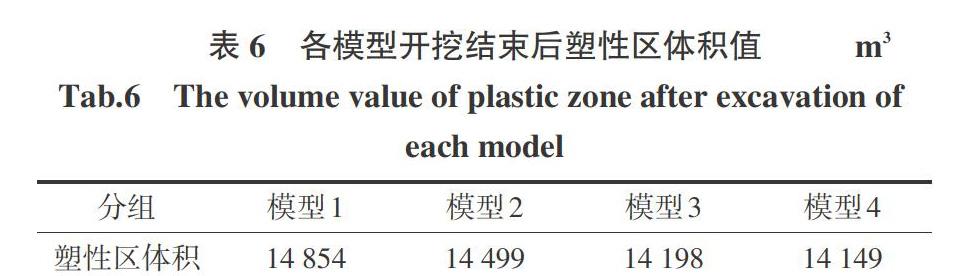
图16为隧道开挖完成后塑性区分布，表6为相应的塑性区体积值统计表。由图16所示，为隧道開挖结束后塑性区分布情况，图中红色为隧道围岩已经发生塑性变形区域，绿色为隧道围岩正在发生塑性变形区域，紫色为隧道初衬已经发生塑性变形区域，棕色为隧道初衬正在发生塑性变形区域。围岩塑性区主要集中在上部偏压土体及隧道初衬周围，浅埋侧隧道上部偏压坡脚地表大部分已经完成塑性变形，深埋侧隧道上部土体由于偏压角度较小，大部分还处在塑性变形过程中;隧道初衬塑性区主要分布在两拱肩及两拱脚之间的上下弧形部分，且顺偏压方向;浅埋侧隧道左拱肩部分与地表塑性区贯通，施工中要加强防护。

从表6可知，随着两主洞开挖掌子面距离的增加，隧道开挖完成后的塑性区体积减小，模型4的塑性区体积要小于其他工况下的模型，对于控制隧道塑性区体积效果最好。

3.5 锚杆受力分析

由于深埋侧隧道开挖后受力较浅埋侧隧道大，锚杆受力图17为选取深埋侧隧道开挖结束后Y=1 m断面处锚杆轴力与砂浆应力分布图，表7为深埋侧隧道开挖结束后Y=1 m断面处各跟踪点锚杆轴力值，图18为深埋侧隧道开挖结束后Y = 1 m断面处各跟踪点锚杆轴力关系曲线。

图17中左边为锚杆轴力图，右边为锚杆砂浆应力图;黑色为受拉，红色为受压。所有模型都一致表现出：隧道开挖结束后锚杆处于受拉状态，锚杆砂浆应力从隧道洞壁沿隧道径向由受压转变为受拉，且发生转变的部位大致在锚杆中部。模型1锚杆砂浆最大应力值为1. 134 MPa，模型2为1. 216 MPa，模型3为1. 138 MPa，模型4为1. 440 MPa。模型4的锚杆砂浆应力值最大，可以为锚杆粘结提供较大的凝结力，加强对围岩的加固作用。

由表7与图18所示，4种不同工况的深埋侧隧道开挖结束后断面Y=1 m处各锚杆跟踪点轴力，受偏压作用影响，拱肩到拱脚轴力均较大;模型4锚杆紧邻洞周的跟踪点处轴力相对最小，这种情况表明隧道衬砌受力较为安全，能保障整体的稳定性。综合来看模型4工况下的锚杆轴力最安全。

4 结论与建议

本文依据头炮隧道实际情况，在确定双侧壁导坑法先开挖深埋侧隧道的基础上，结合实际中小净距隧道工程概况及规范中的建议，将施工时两主洞掌子面间距细分为12 m、16 m、20 m和24 m这4种工况进行隧道开挖数值模拟，从隧道上部边坡位移、围岩位移及应力、初期衬砌位移及应力、塑性区体积及锚杆受力角度分析隧道稳定性。得到以下几点结论。

1）由于上部土体存在偏压的关系，隧道在上部边坡位移影响范围、围岩位移及应力、初衬变形及应力、锚杆受力等方面表现出明显的不对称的现象，影响范围顺偏压方向倾斜，深埋侧隧道由于埋深较深，隧道整体竖向位移和应力影响范围及数值较大，浅埋侧隧道由于位于边坡坡脚位置处，水平位移和应力影响范围及数值较大，而且在坡脚位置处出现了拱起现象，施工中应针对出现的非对称现象采取如非对称锚杆支护、设置抗滑桩、挡土墙、反压回填等相关措施，保证施工安全。

2）边坡位移方面，4种工况模型差别不大，整体都表现为从浅埋侧隧道拱顶上方开始，竖向沉降值的增速变缓，到深埋侧隧道附近时，拱顶位置上方竖向沉降值最大，远离后沉降值变小;水平位移值在隧道跨度范围内，沿上部边坡高度的增加而增加;中夹岩柱上方地表远离了隧道开挖范围并且偏压边坡角度变缓，水平位移值开始显著减小。模型4对边坡位移的控制效果最好。

3）围岩与初衬位移及受力方面，右幅隧道埋深相对较深，拱腰和拱脚位置应力集中现象更为明显，对浅埋侧隧道右拱腰到右拱脚的范围内有影响;浅埋侧隧道拱底部分产生的竖向应力范围上呈现出不对称、沿偏压方向倾斜的特点;模型4竖向及水平位移也最小，竖向应力对周边围岩的影响范围最小，对应力的控制较好，且初期衬砌的支护效果也最好。

4）塑性区方面，随两主洞开挖掌子面间距增加，开挖完成后隧道塑性区体积减小，模型4的塑性区体积小于其他3种工况，对于控制隧道塑性区体积的效果最好。

5）锚杆受力方面，模型4锚杆紧邻洞周的跟踪点处轴力最小，这种情况表明隧道衬砌的受力最安全，能保障整体的稳定性;模型4锚杆砂浆应力值最大，可为锚杆粘结提供较大的凝结力，加强对围岩的加固作用。综合来看，模型4对应工况下的锚杆轴力最优。

综上所述，模型4对应的双侧壁导坑法先开挖深埋侧且两主洞掌子面间距保持在24 m（2倍洞径）左右进行隧道开挖对保证浅埋偏压小净距隧道稳定性的效果最好，可为本工程及相似工程提供参考。

参考文献：

[1]    张运良，扶晓康，刘海林，等. 浅埋小净距偏压隧道合理开挖顺序探讨[J]. 铁道科学与工程学报，2013，10（5）：57-63.

[2]    苗天. 非对称结构偏压小净距隧道施工工法数值分析[J]. 黑龙江交通科技，2017，40（3）：161-162，164.

[3]    腾俊洋，唐建新，张闯，等. 浅埋偏压小净距隧道围岩压力分布与围岩控制[J]. 地下空间与工程学报，2018，14（3）：761-769.

[4]    CHAPMAN D N，ROGERS C D F，HUNT D V L. Prediction of settlement above closely spaced multiple tunnel eonstructions in soft ground[C]// BALKEM A A. Proeeedings of the 3rd International Symposium on the Geotechnical Aspects of Underground Construction in Soft Ground，Rotterdam：2002：299-305.

[5]    DO N A，DIAS D，ORESTE P. 3D numerical investigation on the interaction between mechanized twin tunnels in soft ground[J]. Environmental Earth Sciences，2015，73（5）：2101-2113.

[6]    TIWARI R，CHAKRABORTY T，MATSAGAR V. Dynamic analysis of a twin tunnel in soil subjected to internal blast loading[J]. Indian Geotechnical Journal，2016，46（4）：369-380.

[7]    PATERNESI A，SCHWEIGER H F，SCARPELLI G. Parameter calibration and numerical analysis of twin shallow tunnels[J]. Rock Mechanics and Rock Engineering，2017，50（5）：1243-1262.

[8]    中華人民共和国交通部. JTG D70—2004，公路隧道设计规范[S].

[9]    展国伟，夏玉成，杜荣军. Hoek-Brown强度准则在FLAC3D数值模拟中的应用[J]. 采矿与安全工程学报，2007，24（3）：366-369.

[10]  万战胜，朱岱云，夏永旭. 盾构隧道壁后注浆对地表沉降影响数值模拟研究[J]. 河北工业大学学报，2011，40（1）：110-113.

[11]  杨建华，朱彬. 大跨度软岩隧道开挖方法及施工方案数值模拟研究[J]. 西安科技大学学报，2011，31（3）：287-292.

[12]  黄成林，罗学东，吕乔森. 软岩隧道开挖方法对变形影响数值模拟研究[J]. 铁道建筑，2011，51（11）：35-38.

[13]  李元海，杨苏，喻军，等. 大型溶洞对隧道开挖稳定性的影响分析[J]. 现代隧道技术，2016，53（4）：52-60.