摆动油缸端面密封圈不同轴向预压缩量下接触压力分析*
2021-03-30黄海祺谢良喜
黄海祺 谢良喜
(武汉科技大学机械自动化学院 湖北武汉 430081)
本文作者对叶片式液压摆动油缸端面密封圈在不同轴向预压缩量下的接触压力展开研究,分析了其受力情况及对摆动油缸启动压力的影响。
1 摆缸结构
叶片式液压摆动油缸结构如图1所示,其主要由轴承、盖板、端面密封圈定子、转子组成。

图1 叶片式液压摆动油缸截面Fig 1 Section of RVA
2 端面密封圈密封特性分析
假设摆缸旋转轴向为z轴,沿半径方向为x轴,圆周方向为y轴。为了提高摆缸的端面密封性能,往往在端面密封圈z轴方向增加预压缩量δz,来确保摆缸的密封性能。如图2所示。

图2 叶片密封区截面Fig 2 Section of vane seal area
如图3所示,当摆缸启动时,油液注入工作油腔,油压对端面密封圈的挤压所产生的径向接触压力为px2。由于橡胶能够向各个方向均匀传递流体静压力,得po=px2。

图3 油腔部分截面Fig 3 Section of oil chamber
通过分析端面密封二维模型,用螺钉固紧会使得盖板对其z轴方向产生压力pz,从而产生z方向正应力σz。一旦端面密封圈z轴方向受到挤压,就会产生端面密封圈内圈与转子外壁接触压力和端面密封圈外圈与定子内壁接触压力px。由于σx、σz应力是垂直于接触面,故可将其视为接触压力px、pz。
对于各向同性的弹性橡胶材料,当其变形量很小时,线应变只与正应力有关,而与切应力无关;切应变只与切应力有关,而与正应力无关。由广义弹性胡克定律[9-10]可知,其应力应变关系符合弹性力学理论:
(1)
式中:εx、εy、εz为3个方向上的应变;σx、σy、σz为3个方向上的应力;λ为密封材料泊松比;E为密封材料弹性模量。
公式(1)中,εx、εy和εz分别为橡胶密封在x、y和z方向的法向应变,其定义为
εx=δx/bx,εy=δy/by,εz=δz/bz
(2)
式中:δ和b分别是橡胶密封在安装后的压缩变形量(密封过盈)和其压缩前的初始尺寸。
考虑到压缩对密封件的影响,这里设压缩应变为正,而拉伸应变为负。对于端面密封与叶片密封接触部分,其接触面为平面,法向应变为
εz=(ΔL)/L=δz/L
(3)
式中:δz为端面密封圈轴向预压缩量;L为端面密封圈轴向预压量为0时的厚度(端面密封轴向初始尺寸)。
转子、定子和盖板均采用45调质钢,弹性模量为210 GPa。聚氨酯制成的密封材料弹性模量一般在10~30 MPa之间。由于2种材料的刚度相差数万倍,且钢的硬度远远高于聚氨酯材料,所以转子、定子和盖板因端面密封圈受到挤压而产生的形变可以忽略。由于端面密封圈x轴方向没有预压缩量,可设端面密封圈x轴向应变εx=0。
根据以往实验所得数据,在z方向所增加的预压缩量产生的应变均少于20%,并且没使其发生明显变形。当弹性材料处于弹性形变阶段,一般通过橡胶应力应变公式求出端面密封圈与叶片接触所产生的正应力。
求得正应力σz对应产生z轴方向的压力pz为
pz=(δz/L)E
(4)
综上所得径向x轴产生的接触压力px为
(5)
3 端面密封圈有限元分析
对端面密封圈进行有限元分析,工程上一般采用大型非线性有限元软件Abaqus,该软件的计算精度高,能较好模拟真实系统[11]。对于端面密封圈这类环形密封元件,因其具有轴对称的特征,一般可简化为轴对称模型。由上文可知,转子和定子的弹性模量远大于聚氨酯材料,因此可将其看成解析刚体,而端面密封圈简化为可变形体。使用三维有限元方法不仅可以更真实还原实际情况,而且可得到理想的计算结果。为了充分展示Abaqus有限元分析软件的能力,有必要对研究模型进行适当简化与合理划分网格。同时保证模型中各材料、零件结构和尺寸与端面密封圈实物相同,如图4所示。

图4 模型网格划分Fig 4 Mesh division of the model
按照图2和图3,详细的边界条件和分析步骤为:将端面密封圈与盖板的接触面、转子外圈与端面密封圈内圈的接触面和定子与端面密封圈外圈的接触面固定;设定适当的分析步,将刚体和密封橡胶使用面-面接触的方式,模拟端面密封安装的预压缩过程。
对端面密封圈进行有限元分析时,采用非线性的Mooney-Rivlin本构模型进行计算。按Mooney-Rivlin模型所计算的参数设置[12],取C10=1.87 MPa,C01=0.47 MPa, 有限元分析结果如图5、图6所示。

图5 端面密封圈在不同轴向预压缩量下的应变云图Fig 5 Strain cloud diagram of end-face seal under different axial precompression (a)0.5 mm;(b)1.0 mm;(c)1.5 mm;(d)2.0 mm
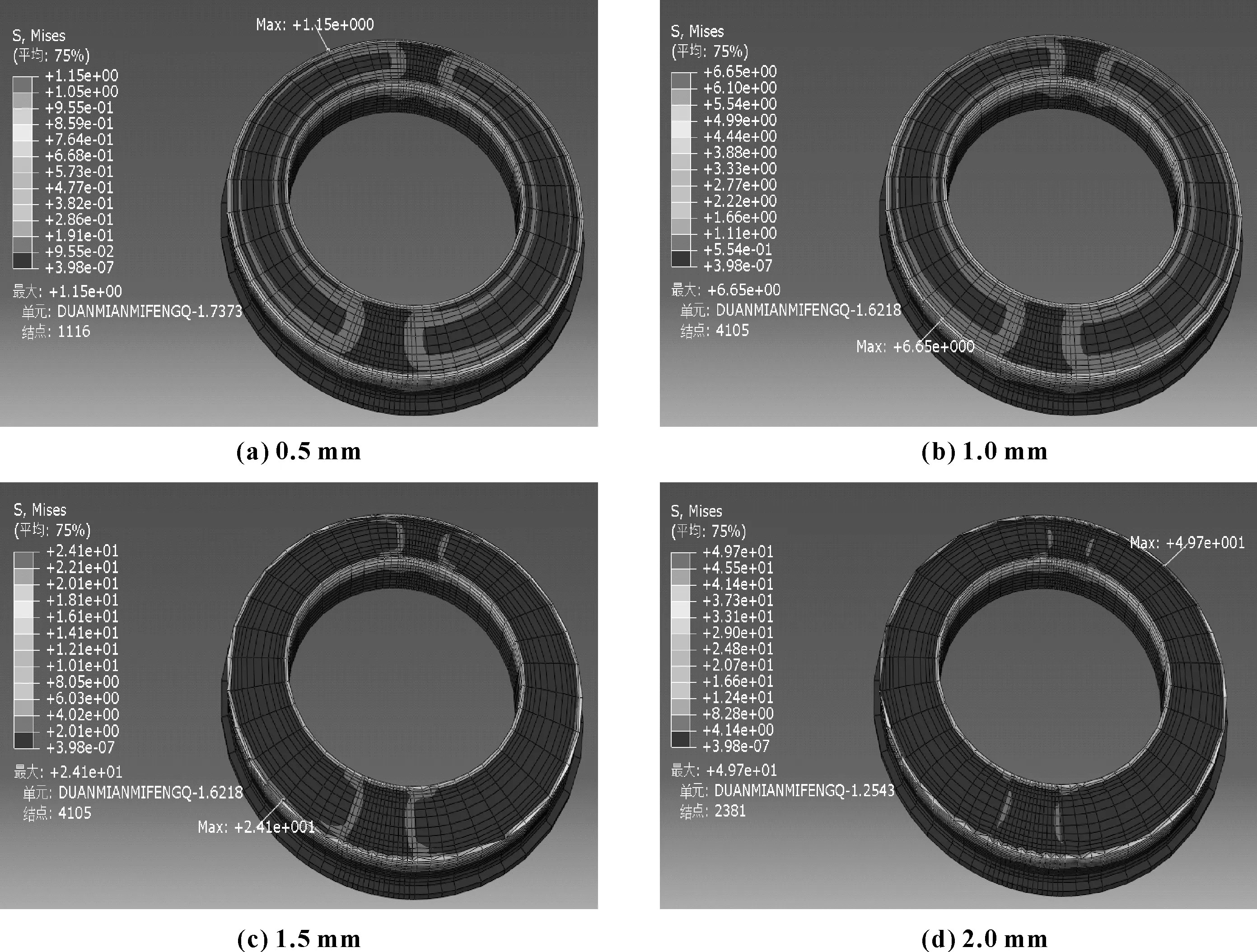
图6 端面密封圈在不同轴向预压缩量下的应力云图Fig 6 Stress cloud diagram of end-face seal under different axial precompression (a)0.5 mm;(b)1.0 mm;(c)1.5 mm;(d)2.0 mm
由图5和图6可知,随着轴向预压缩增加,密封接触面均发生微变形。应变应力集中出现在密封圈外圆环表面密封接触面,其次是内圆环密封接触面,同时可以清晰观察到密封接触面被挤压的轨迹。
4 预压缩量对启动压力的影响
4.1 理论分析
在启动状态下,端面密封圈预压缩量所产生的接触压力难以实验测量,一般通过摆缸启动压力来间接验证。摆缸启动压力的摩擦力主要受密封接触部分的影响,通过绘图软件对相应的接触面积进行测量,结果见表1。表中:So为油压作用于端面密封圈对应的接触面积;θ为叶片夹角;Sn为转子与密封圈内环接触总面积;Sye为油压作用在叶片上的面积。

表1 不同状态下接触压力对应的接触面积Table 1 Contact area corresponding to contact pressure at different states
综上所述,摆缸启动压力与端面密封圈轴向预压缩量的关系公式为
poSye=μpxSx+μpzSz+μpoSo
(6)
式中:μ为钢制材料与聚氨酯材料的摩擦因数,μ=0.18。
将式(4)(5)代入式(6)变形得:
(7)
用作密封的橡胶材料的预压缩量通常用压缩尺寸与原始尺寸的百分比即压缩率表示。一些文献中密封橡胶泊松比取λ=0.485~0.5,文中采用的泊松比为0.496。其弹性模量E通常不是定值,而是与应变相关的变量。英国学者NIKAS博士在文献中为了简化计算,假定弹性模量E=24 MPa,泊松比λ=0.49,其使用前提是应变不应超过10%~15%[13-14]。若考虑到橡胶材料的非线性问题,比较常见的处理方式是采用Mooney-Rivlin超弹性材料模型。应用该模型需设定Mooney-Rivlin常数,通常可通过单轴拉伸或压缩试验得到,也可以查阅相关文献。橡胶的机械性能具有明显的非线性,即在弹性范围内其应力-应变曲线不是简单的直线。一些文献中的橡胶密封Mooney-Rivlin常数取值为C10=1.87 MPa,C01=0.47 MPa,D1=0[15],其在应变不超过50%时的应力-应变关系曲线如图7所示。
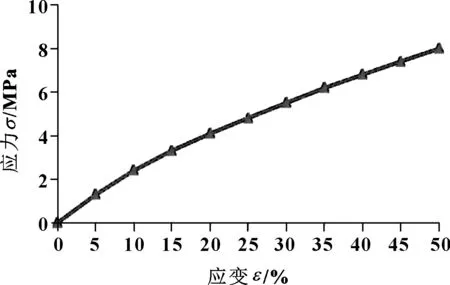
图7 橡胶密封应力-应变曲线Fig 7 Rubber seal stress-strain curve
由图7可见,橡胶密封材料的弹性范围内的应力-应变曲线并不是简单的直线。因此,在求解密封面接触压力时,如果需要考虑材料的非线性特性,可以首先计算橡胶密封的应变值,然后根据应变值查询图7得出对应的应力。
根据实验经验,端面密封圈z向预压缩量所产生的应变一般不超过20%。因而选择端面预压缩量应变在20%内的范围进行研究,分成4个不同应变范围,采用对应弹性模量E。当z方向初始尺寸为10 mm时,端面密封圈密封对应不同压缩量,所得的压缩率和弹性模量值如表2所示。

表2 橡胶密封在不同预压缩量下的压缩率和弹性模量Table 2 Compression rate and elastic modulus of rubber seal under different precompression
综上所述,绘制端面密封圈轴向预压缩量与摆缸启动压力关系图,如图8所示。

图8 端面密封圈轴向预压缩量与摆缸启动压力关系Fig 8 Relationship between axial precompression of end-face seal and starting pressure of RVA
4.2 实验
根据以往实际加工经验,对于该尺寸摆缸的轴向预压缩量经验值取0.2~0.8 mm之间。因为预压缩量过小有可能会导致摆缸发生内泄,且还要考虑加工成本等因素。为了提高摆缸密封性能,同时又需要满足耐压实验,往往选择较大的预压缩量0.6 mm进行实验,对摆缸进行多次测试。
实验在如图9所示的摆缸上进行,结果如表3所示。可见,实际启动压力比理论启动压力略大。因为实际安装过程易产生一定安装误差,故启动压力的实际值与理论值误差在0.5 MPa范围内。该误差为可接受范围,验证了理论分析的准确性。

图9 实验摆缸实物Fig 9 Physical picture of experimental RVA

表3 摆缸启动压力实验结果Table 3 Starting pressure record of RVA
5 结论
(1)对端面密封圈的受力情况进行理论建模,分析了其接触压力,发现最大应变与应力均分布在端面密封圈外圆环与内圆环密封接触处,可为端面密封圈结构优化提供借鉴。
(2)分析了端面密封圈轴向预压缩所产生的接触压力对摆缸启动压力的影响,随着预压缩量的增加,其对应的启动压力也增大;由于不同的弹性模量,两者的关系为非线性相关。
(3)通过实验,可得实际结果数据逼近理论分析预期结果数据,验证了所建立理论模型的可行性。
