耦合KL理论与调度特征的大规模水电站群优化调度降维方法

申建建，张 博，程春田，李秀峰，蒋 燕，赵珍玉

（1.大连理工大学 水信息研究所，辽宁 大连 116024； 2.云南省电力调度控制中心，云南 昆明 650011）

1 研究背景

水电系统调度是一类非凸、非线性、多变量、高维数且具有庞大约束条件集的大规模复杂决策优化问题，也一直是国内外公认的最具挑战性的理论和实践课题之一[1-3]。水电调度优化计算规模与参与的水电站数、时段数、状态变量（初库容）离散数、决策变量（末库容、流量、出力）离散数、水库不确定径流离散数紧密相关[4]，且随着电站装机规模、库容离散数目、水电站数目等参数的增大，计算的时空复杂度呈指数增长，这一特征使得求解几十、上百座电站的大规模水电系统优化问题需要的计算耗时和存储空间均急剧增加，“维数灾”问题突显[5]。对于我国西南特大流域梯级水电站群、省级电网跨流域水电系统、区域电网跨流域跨省水电系统而言，如何有效突破超大规模水电站调度建模求解特别是效率问题已成为水电及电力系统运行面临的重要理论和技术障碍[6]。

国内外很多研究工作聚焦水电系统降维问题，涉及以下几个方面：（1）从减少优化电站数出发，提出了动态规划逐次逼近方法（DPSA）、聚合-分解方法等，前者通过减少单次优化的电站数，将多电站高维优化问题转换为单一电站低维优化问题，后者则将多个电站聚合为虚拟电站，以减少整体的优化电站数。从减少优化阶段数出发，提出了逐步优化方法（POA）[7]、变尺度方法[8]等；（2）从减少离散状态数出发，提出了离散微分动态规划（DDDP）[9]、离散梯度逐步优化方法[10]、正交试验设计方法[11]等。其中，正交试验设计方法是通过“均衡分散”抽样将单阶段各电站不同离散状态之间的组合视为一次多因素多水平试验优选，以减少计算的状态组合数；（3）从简化问题复杂性出发，提出了线性或分段线性规划、非线性规划等方法[12]，前者是对水电系统的各种非线性曲线或函数进行线性或者分段线性处理，或者通过固定发电水头、尾水位等进行问题简化，以减少问题求解的复杂性；后者利用二次或者高次多项式重构目标函数和曲线方程以形成可求解的优化调度模型。

对于超大规模水电系统而言，如何高效求解显得尤为重要。从启发式算法的角度出发，通过随机搜索启发式策略求解多目标问题，以提高问题的求解效率[13]。从计算技术角度出发，通过识别系统的可并行性，利用计算机并行计算资源可以提高计算效率[14]。此外，近年来兴起的机器学习、云计算、智能算法等也为超大规模水电系统高效求解提供了新的思路，例如利用量子理论改进智能群体搜索方法的编码模式和搜索模式，并结合启发式策略动态处理短期水电调度中最小正常运行时间/停机时间约束和旋转备用容量等复杂约束，以提高求解效率和结果精度[15]。

总体而言，不同降维方法提供了不同的视角解决水电系统维数难题。本文考虑水电站长系列调度过程，以文献[16-18]提及的Karhunen-Loève展开方法为基础，提出一种大规模水电站群优化调度降维方法，通过对水电站群长系列调度样本进行主成分分析，识别调度过程中的库水位变化特征值与其对应的特征函数，采用KL方法将库水位序列描述为前述水位变化特征项的线性函数，并通过各项的随机系数组合确定特定来水对应的发电调度过程；针对前述文献中随机系数分布和遗传算法优化随机性可能导致的结果实用性和准确性核心问题，引入Kullback-Leibler 散度以根据问题特点优选适合的特征项随机系数概率分布，并建立了两阶段迭代寻优策略实现特征项系数的高效、稳定求解。该方法的有效性、高效性、以及随机系数分布规律和参数敏感性通过云南电网省调大规模水电系统进行验证。

2 水库群优化调度数学模型

采用经典的发电量最大模型进行水电优化调度降维方法分析，其目标函数为：

约束条件为：

（1）水量平衡方程：

（2）库水位、发电流量与出力限制：

（3）水库调度期始末水位限制：

（4）水位-库容关系：

（5）尾水位-泄量关系：

（6）系统出力带宽约束：

式中：I为参与计算的总电站数；i为电站编号；T为调度期时段数；t为时段序号；Qei，t为t时段电站i的发电流量，m3/s；Hn，t为t时段电站i的发电水头，m；Δh为单一时段小时数，h；Vi，t为时段t水电站i的初始库容，m3；Qui，t为时段t电站i所有直接上游水电站的出库流量之和，m3/s；Qai，t为时段t电站i的区间流量，m3/s；Qoi，t为时段t电站i的出库流量，m3/s；Δt为时段内秒数，s；分别为电站i在时段t的库水位下限与上限，m；分别为电站i在时段t的出库流量下限与上限，m3/s；分别为电站i在时段t的发电流量的下限与上限，m3/s；分别为电站i在时段t的出力下限与上限，MW；Zi，0为调度期水电站i的初始库水位，m；Zi，T为调度期末水电站i的库水位，m；Vi，t为t时刻水电站i的水库水量，万m3；Zi，t为t时刻水电站i的水库水位，m；qi，t为t时刻水电站i的下泄流量，m3/s；hi，t为t时刻水电站i的尾水位，m；分别为电站i在时段t的出力下限和上限，MW。

3 耦合KL理论与调度特征的水电调度方法

3.1 总体思路本文思路是采用谱优化方法中的Karhunen-Loève展开（以下简称KL展开），通过实际调度历史样本分析与特征提取，将待优化调度决策看作一个需要进行模拟的随机过程，利用从样本中提取的特征项构建随机过程表达式，通过特定分布的随机变量确定各个特征项的线性组合，有效减少决策变量的个数，从而达到降维目的。KL展开可以对复杂多变量随机过程进行高效处理，将其描述为若干正交向量与特征值的展开式。其中，特征值和特征向量需要采用主成分分析方法，从水电站群长系列实际调度样本进行识别提取；特征项的随机变量应该采用何种分布进行组合计算，需要结合问题特点优选适合的概率分布。KL方法的整体求解见图1。

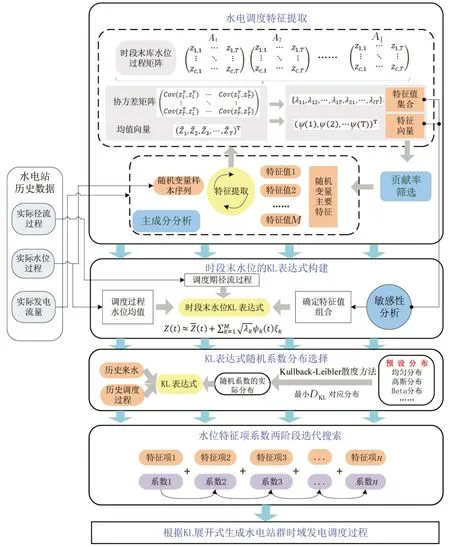
图1 方法原理

3.2 KL理论KL理论又被称为本征正交分解，本质是将一个随机过程按几组正交特征函数分解为多项式和的形式，以此来近似拟合原随机过程，KL分解涉及确定性函数（即特征函数ψk（t））和随机变量（ξk）的级数展开，其中确定性函数由自相关核函数确定，随机系数ξk的概率分布由于随机过程本身信息的缺乏通常难以直接确定。

KL展开的基本表达形式以一个可测度事件集合为基础，用于描述物理随机过程。设构成随机过程事件集的函数为为事件对应的随机过程检索序号系列，θ为该随机事件。则根据KL展开理论，表达式为：

其中随机系数ξk应遵循以下数学定义：

具体来说，通过式（13）仅能证明随机变量的均值为0、方差为1，并且是相互正交的。通过式（13）可知，KL展开式中各事件描述函数对应的随机系数与事件本身有密切联系，因此在针对不同特点的物理过程进行建模时，如何选择符合实际数据特征的连续或离散概率分布赋给随机系数ξ(θ)是非常重要的，这一问题可以通过下文3.5节方法有效处理。

按照上述思路，本文采用截断型KL展开式对水电站的时段末水位过程进行表达，具体为：

式中：Z（t）为水电站t时段末的库水位；为实际调度样本集中t时段末的库水位均值；λk与ψk(t)为正交特征值与对应的特征向量；ξk为一系列独立的随机变量，其分布遵从均值为0，方差为1，在求解过程中，该系数为问题的决策变量。在求解过程中，ξk的概率分布形式直接影响到计算模型的收敛速度以及结果精度。该分布可以选取符合均值为0、方差为1 的均匀分布、高斯分布或者Beta分布等。

利用式（14）解决离散型随机过程问题时可以进行离散近似处理，一般选择有限个数的离散特征项进行KL展开，所以库水位变量的KL展开式可表述为：

式中，M为样本选取特征项的个数，其大小取决于结果精度要求以及样本中各随机过程之间的相关性。精度要求越高，则需采用的特征项个数越多。M的取值存在一定范围，这取决于主成分分析的计算结果。实际调度样本集数据的相关性越强，则特征项数目越少，M的上限取值越小。反之，则得到的特征项数目偏多，M的上限数值变大，这种情况下需要在求解过程中对M值以及采用的特征项进行优化计算以便于权衡选择。

可以看出，在采用KL展开方法过程中，水电站的调度决策变量从原先的时段末水位转变为针对调度期若干特征项的系数，以此来确定调度期的库水位过程。进一步分析该方法的时间复杂度，一般而言，水电调度问题始、末都只有一个状态变量，假定其余T-1个时段的状态变量离散为S份，则对于经典DP算法，单个水库的计算次数为S T-1，I个水电站的时间复杂度为O（TSI(T-1)）；对于POA算法，计算次数与其迭代收敛条件有关，若算法收敛终止前整体需进行n次迭代，则算法的时间复杂度为O（nSI(T-1)）；对于KL 展开方法，假定水电站的特征值个数为ki，特征值可选离散权重值为n，单个水电站收敛需计算次数为si，则KL 展开方法的时间复杂度为O（Isi ki n）。可以看出，KL 展开方法的复杂度显著低于经典的DP及改进方法。

3.3 建立发电调度过程样本集在采用主成分分析法提取水电站调度过程特征值与特征向量前，需要建立各水电站的发电调度过程样本集。对于具有长系列实际调度数据的电站，直接采用历史的库水位过程作为样本，见公式（16）；对于缺少实际调度数据的电站，以长系列径流为输入，以式（1）为目标函数，采用经典的DP进行优化计算获得发电调度过程，其样本表达式与下式相同：

式中：Ai，sample为电站i的调度过程样本集集合；zc，j为第c种来水情况下第j个时段的时段末库水位；T为电站i调度过程中包含的时段数。

在后续章节计算具体算例过程中，由于无足够长系列的水库实际生产过程，因此对单库采用DP计算其历史各年份来水情况下的调度过程作为调度样本以模拟单库的多年实际调度过程，对多库则采用POA计算其历史各年份来水情况下的调度过程作为调度样本以模拟多库梯级的多年实际调度过程。

3.4 主成分分析方法计算样本特征项主成分分析（PCA）是一种经典的数据分析方法，原理是将数据的n维特征映像到k维上，在这一过程中将得到一组新的正交向量（映射基底），其对应的特征值与向量本身即为构建KL展开式所需的特征函数。本文主要应用此方法于从水电站的长系列调度过程样本集中提取水位特征值和特征向量。

根据PCA方法原理，需要分别求解矩阵各电站的协方差矩阵Cov(Ai，sample)，见下式：

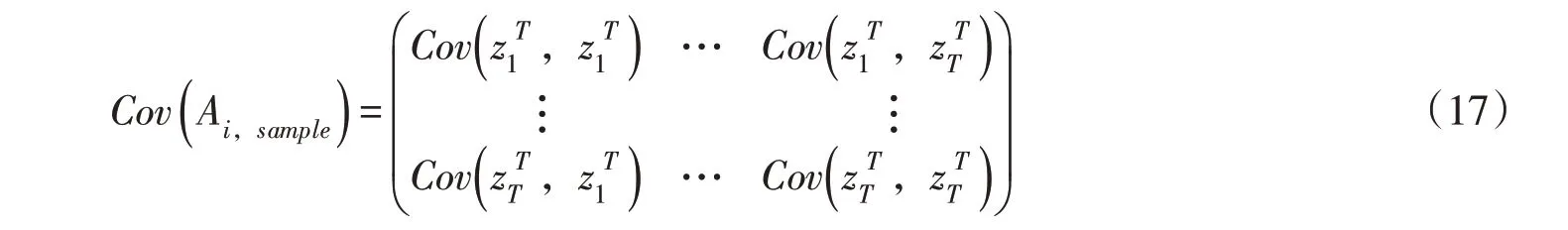
按照式（17），可以得到I个协方差矩阵Cov(A1，sample)，……，Cov(AI，sample)。对每个矩阵分别计算特征值与特征向量，得到特征值系列{λ11，λ12，…，λ1T，λ21，…，λIT}，每个特征值对应的特征向量ψkT应满足下式：

由此计算出各特征值对应的特征向量。

考虑到每个协方差矩阵均会计算得到T个特征值与其对应的特征向量，所以需要优选能够代表水电站调度过程的主要特征值。本文引入累积贡献率指标，将同一矩阵求出的特征值按从大到小排序{λ1，λ2，…，λn}，累积贡献率求解公式如下：

式中：Kd为λd的累积贡献率；N为特征值总数；d为计算累积贡献率的特征值序号。

在PCA方法中，累计贡献率又称累计方差贡献率。在实际计算中，特征值从大到小排序，然后从前到后求和即可得到累积方差。所以Kd的大小表示了λ1，λ2，…，λd携带原数据信息的比例。实例计算分析中，根据保留不同主成分所建立模型的精度，综合考虑保留主成分的累计贡献率的阈值。

3.5 利用样本特征项建立各水电站KL展开式 利用3.2节给出的KL 展开描述方法，可以确定任一水电站i在t时段末的库水位，见下式：

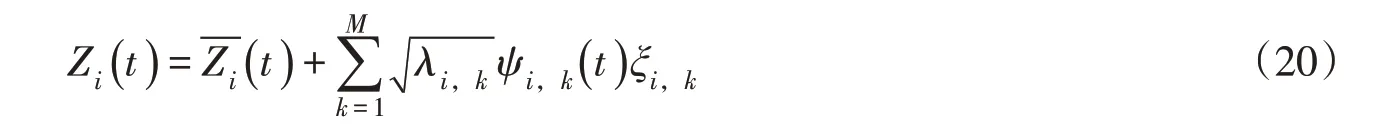
按照上式建立任一水电站i的时段末库水位描述方程，并对每个特征项对应的系数ξi，k进行优化求解，主要包括以下两部分。

（1）确定特征项系数的概率分布与初始值。在式（20）中，M个特征值对应系数为ξi，k，1 ≤k≤M。由于各ξi，k服从的概率分布均符合均值为0、方差为1，所以如何从各类可选连续分布中优选适合的分布形式并确定随机系数的可行域和初始值是非常重要的。通过分析电站历史调度过程样本集，可以有效预判KL展开式随机系数的概率分布，使后续建模更符合工程实际。

本文引入Kullback-Leibler散度这一概念来衡量KL特征项对应随机系数的实际概率分布与优化计算时假定的概率分布之间的信息误差。这一概念起源于概率论与信息论。Kullback-Leibler 散度与相对熵、信息散度和分辨信息密切相关，表示两个概率分布p(x)和q(x)之间差异的非对称度量。具体来说，p(x)与q(x)的Kullback-Leibler 散度，即DKL(p(x)，q(x))，是对q(x)用于估计p(x)时所丢失的信息的度量。设p(x)和q(x)是离散随机变量x的两个概率分布，对总体X中的任意点，p(x)＞0，q(x)＞0。则DKL(p(x)，q(x))可按照下式进行计算：

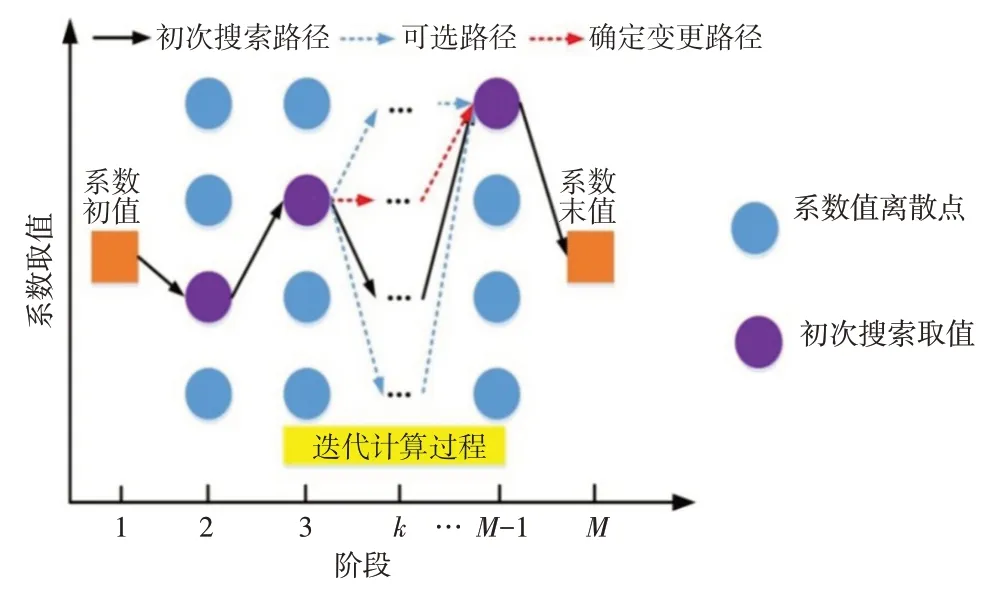
图2 特征项系数迭代计算原理

对任一参与计算电站而言，在确定特征值与特征向量后，可按照下述方法确定KL建模随机系数的概率分布：①步骤1。按照KL展开式（20）以及历年实际调度过程，通过求解线性方程组确定不同年份来水情况下的{ξi，1，ξi，2，…，ξi，T}，其中M=T，即按照式（18）得到的特征项构建式（20）；②步骤2。按照电站的主要特征项，选择对应的随机系数值集合Sy={ξi，1，ξi，2，…，ξi，M}，其中y为历史调度过程样本中包含的年份序号；③步骤3。假定电站共有Y个年份样本，则主要特征项随机系数样本集为S={S1，S2，…，SY}；④步骤4。根据样本S得到KL 建模中各主要特征项对应随机系数ξi，k的概率分布p(x)；⑤步骤5。利用式（21）计算预先设定可采用分布q(x)与p(x)之间的Kullback-Leibler散度DKL(p(x)，q(x))；⑥步骤6。选定DKL最小值对应的q(x)概率分布描述电站KL建模中的随机系数，确定随机系数的可行域以及初始值。

（2）迭代搜索特征项系数。迭代搜索方式如图2所示。以随机系数初始值为基础，采用两阶段迭代优化其取值。对于任一特征项系数ξi，k，固定其余特征项系数，以步长Δs生成可行域范围内的所有系数状态值，按照式（20）计算Zi(t)，并由式（1）计算目标函数值，选择目标值最大的ξi*，k作为特征项ξi，k面临阶段的最优值；采用同样思路逐次对其余阶段的特征项系数进行迭代寻优，直至满足给定的收敛条件。

3.6 耦合KL理论和调度特征的水电调度求解方法流程流程如下：（1）基于水电站实际运行数据，采用3.3节方法构建发电调度过程样本集；（2）提取每个电站的调度特征值与特征向量。对得到的样本集进行主成分分析，获得特征值λk与对应的特征向量(ψ(1)，ψ(2)，…，ψ(T))T，具体方法见3.4节；（3）优选各电站的关键特征值。按照式（19）计算各特征值的贡献率，并按照选定的Kd阈值确定关键特征值系列{λ1，λ2，…，λD，D}为满足阈值的最后一个特征值序号；（4）通过计算3个代表年情况下实际随机系数分布与各预设分布的DKL值，确定电站KL表达式中随机系数的概率分布；（5）构建各电站的KL展开式。以步骤（3）得到的关键特征值为输入，采用式（20）建立每个电站时段末库水位的KL展开式；（6）优化特征项系数ξk。采用迭代方法，初设迭代次数为l=0，单次迭代的计算过程见3.5节；（7）设l=l+1，采用相对误差法判定是否收敛。若则判定算法收敛，计算结束。其中Gl为第l次迭代梯级总年发电量值。在迭代过程中Gl的值单调增加至趋于平稳，变化值符合收敛条件则为目标最大年发电量。若未收敛，调用3.5 节方法进行计算；否则，转至步骤（7）；（8）按照式（20）确定各水电站的调度过程，计算终止。

4 计算实例

4.1 工程背景云南水能资源可开发量近1亿kW，居全国第二位，主要分布在金沙江、澜沧江、怒江、红河和珠江等水系。现阶段，云南省调水电系统包括大中型水电站170 多座，水电装机容量约6667万kW，是我国水电装机规模最大的省级电网之一，占全网发电总装机比重超过70%。对于如此庞大规模的水电系统，在日常发电调度计划编制和调度方案分析中，如何同时保证较高的计算效率和结果的实用性，是极其重要的。本文以云南省调超百座电站的水电系统为对象进行方法验证，设计了3个实例，分别验证方法的有效性、高效性、KL特征项选择对计算方法的参数敏感性以及系数分布形式的选择。实例1、实例2分别以单一大型水电站水库、小湾-糯扎渡双库为对象，对比不同来水场景下KL-两阶段迭代搜索方法与经典DP方法的结果精度和时间；实例3以云南省调所有水电站为对象。整体的计算程序采用JAVA 语言编制，并在处理器为Intel Core i5-2400 3.10GHz，内存4GB的DELL商用台式计算机上完成计算。

4.2 方法有效性检验为验证KL方法求解水电站（群）优化调度问题的有效性，采用丰、平、枯三个典型年对小湾电站、小湾-糯扎渡梯级两种情况进行长期优化调度计算。由于传统DP算法具有全局最优性，通过KL方法与经典DP算法结果进行对比，分析方法的有效性。计算结果如表1、表2所示。

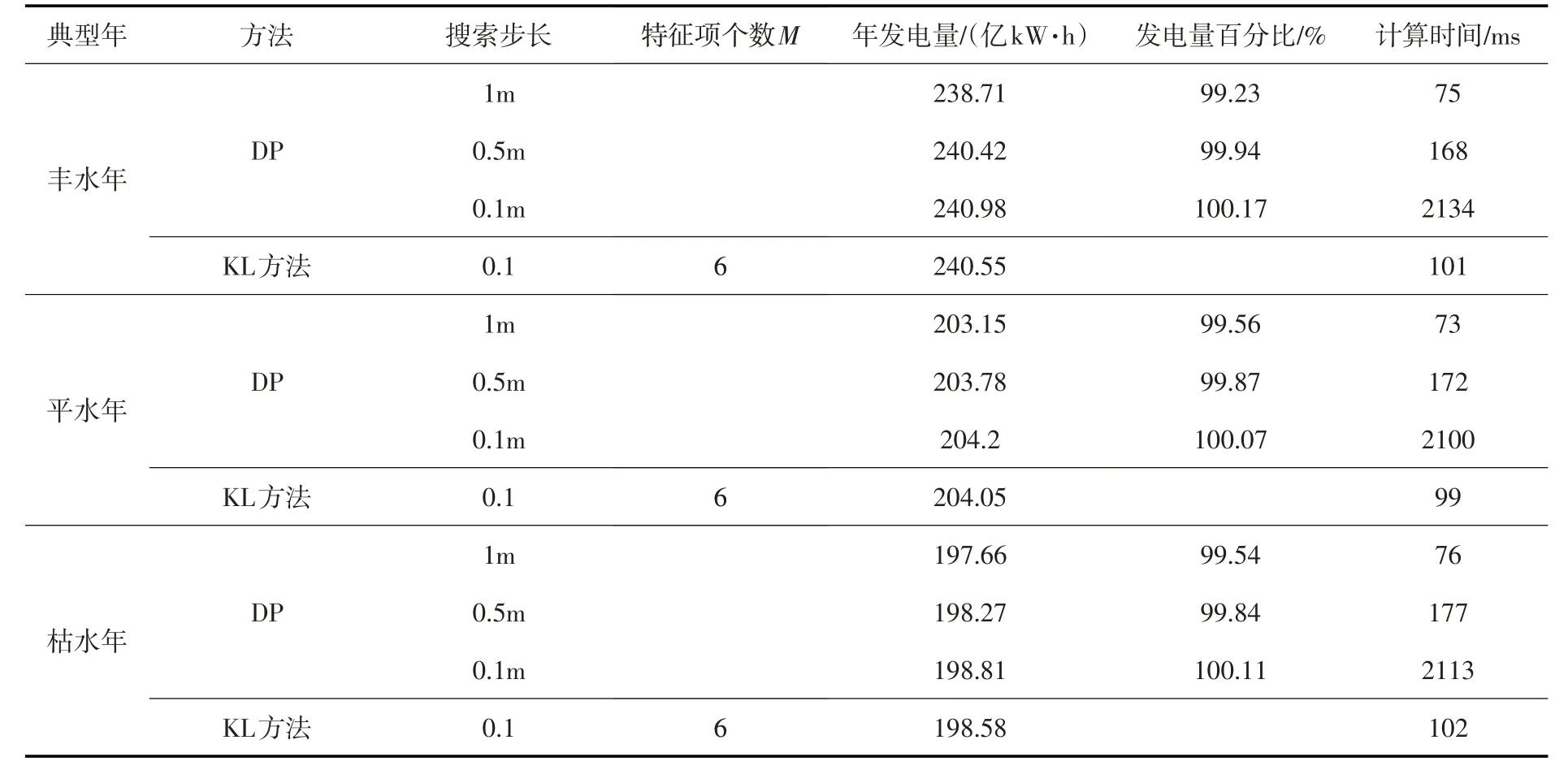
表1 小湾电站两种不同方法的计算结果

实例1中，在小湾单站情况下，KL方法得到的年发电量高于DP在1 m、0.5 m离散步长时的最优结果，增幅范围在0.06%～0.77%；当DP的步长减小至0.1 m时，两种方法的计算结果基本一致，但DP的计算耗时是KL方法的21倍左右。与DP方法的离散全局最优特性相比，KL方法主要对DP方法优化得到的样本进行特征提取，并按照实际入库流量过程与目标函数拟合最优调度过程，所以在DP离散精度较高情况下，总电量可能略小于DP算法。

为进一步验证两种方法在计算效率及结果精度上的差异，在实例2中选取小湾、糯扎渡梯级水电站进行优化调度计算，结果如表2所示。

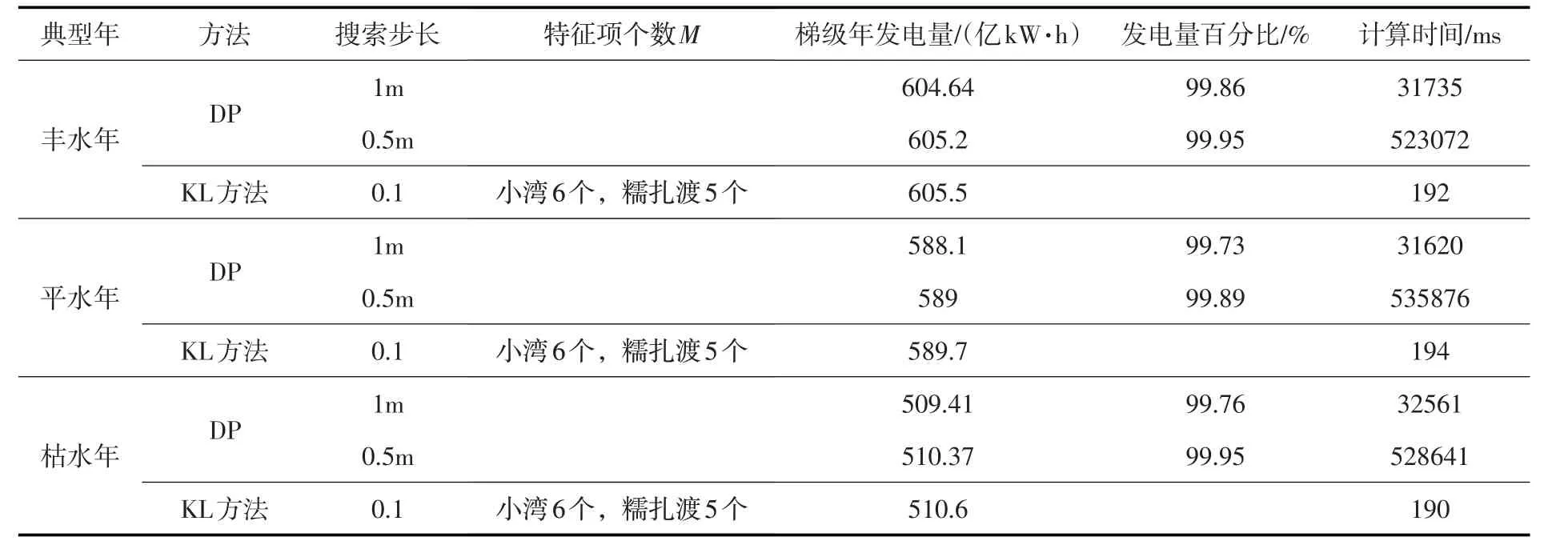
表2 小湾-糯扎渡梯级水电站计算结果

从表2可以看出，对于小湾-糯扎渡梯级水电站，DP方法由于单一阶段状态数增加较多，计算效率明显下降。在同一步长条件下，增加一个电站使计算耗时增加超400余倍，呈指数增长，“维数灾”问题突出。相比较而言，KL 方法在两个电站情况下，计算耗时仅比单站计算耗时增加1.86～1.95倍，与上文3.2节的复杂度理论分析结果一致，体现了较高的计算效率。

从结果中看到，在0.1 m 离散步长下的小湾DP 计算结果好于KL算法。此处KL算法为依据历史调度过程样本对最优调度过程的一种模拟，并不是一种严格的全局最优解，而DP的解在离散范围内为全局最优，所以当DP离散搜索步长减小到一定程度时得出的优化结果确实要好于KL方法，但同时其需要付出足够的时间代价，这对于超百座大规模水电系统而言，就会面临严峻的“维数灾”问题。

4.3 方法的高效性检验为验证方法的高效性，实例3以参与云南省调平衡的所有水电站为对象进行验证，其中部分中小流域梯级在实际运行中一般简化为虚拟电站，所以实际计算电站数为103座。在计算过程中，季调节及以上水电站水库参与优化调度，其他调节性能较差的水电站按照定水位方式进行水能计算。由于来水过程对梯级水电站群的调度计算有较大影响，所以文中采用澜沧江、金沙江、怒江、珠江、红河等主要流域约50年径流资料进行频率分析，确定多个不同频率的典型年径流场景。

考虑到参与优化的电站规模较大，采用DP方法很难在有效时间收敛到合理结果，所以本例采用POA方法进行对比分析，以此评价KL方法的计算效率。各主要流域计算结果见表3，云南水电系统整体计算耗时及总年发电量见表4，计算过程中各流域主要电站的装机容量与提取的特征值个数见表5。

从整体计算结果来看，不同来水场景下KL方法的发电量均略高于POA；从计算耗时角度分析，KL方法的总计算时间平均为10 s左右，POA方法为42 s左右，其计算效率约为后者的4.2倍。另一方面，KL方法考虑了电站的历史调度样本，对各种径流情况的适应性更强，尤其随着实际调度资料的不断延长，提取到的特征变量代表性会更好，算法的整体收敛效率和收敛结果会不断得到改善。计算表明，在采用30、40、50年不同长度历史径流系列对应的调度样本进行KL建模优化计算时，流域中主要电站小湾和糯扎渡可提取的主要KL特征项均减少2个，其最终梯级年发电量也仅为当前优化结果的97.2%，侧面反映出了KL方法优化调度对历史调度经验性的耦合。

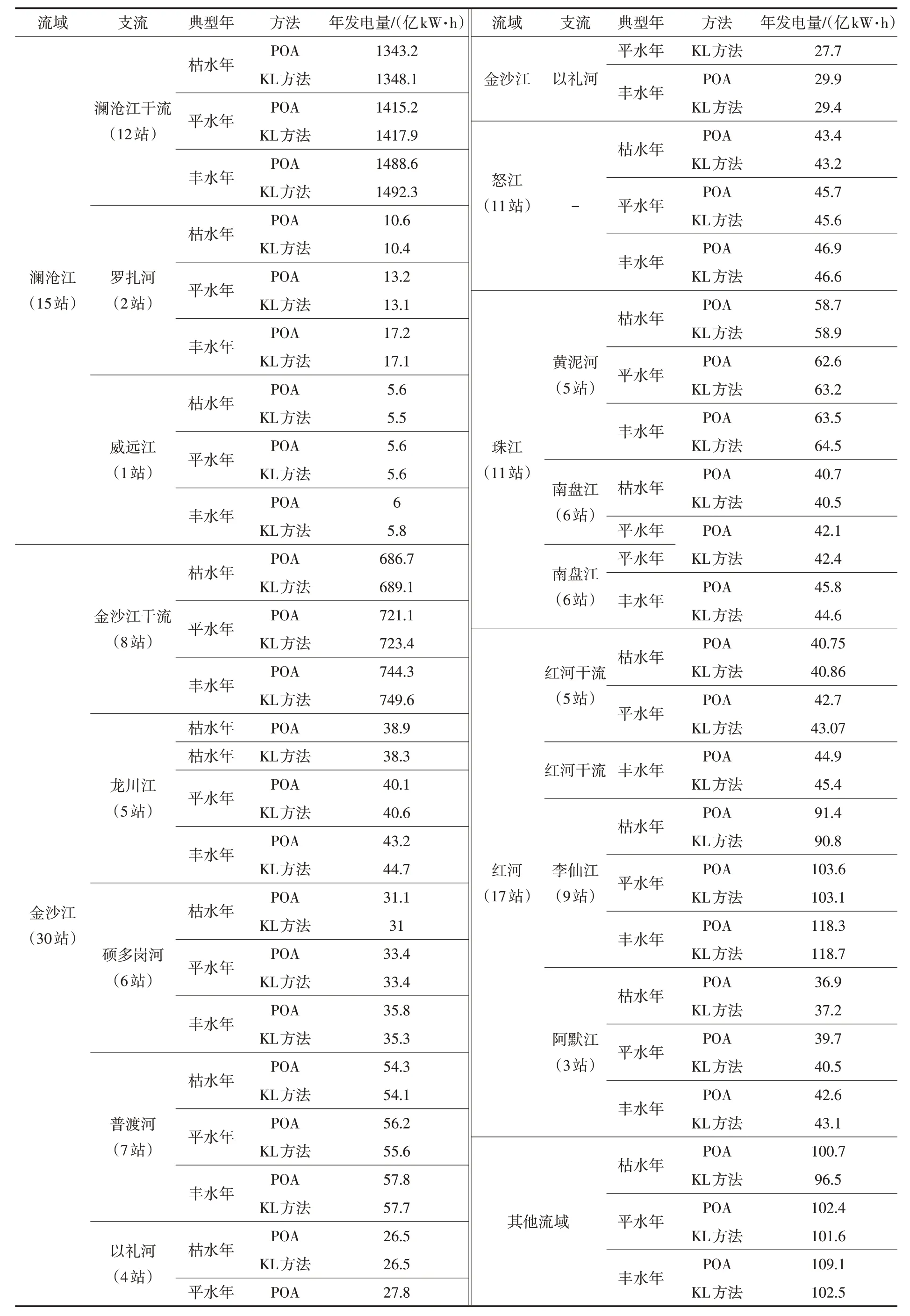
表3 云南主要流域梯级水电站优化计算结果

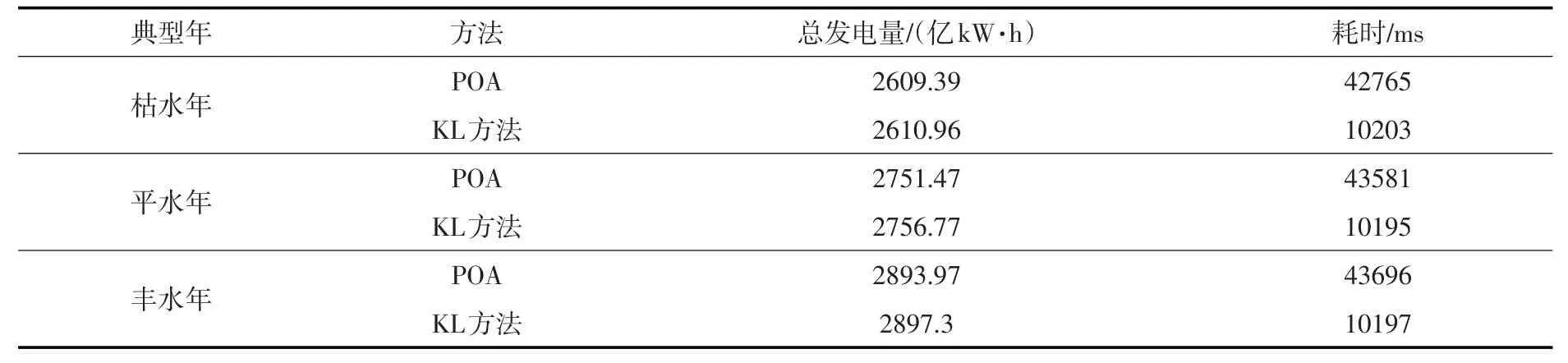
表4 云南水电系统总年发电量及计算耗时

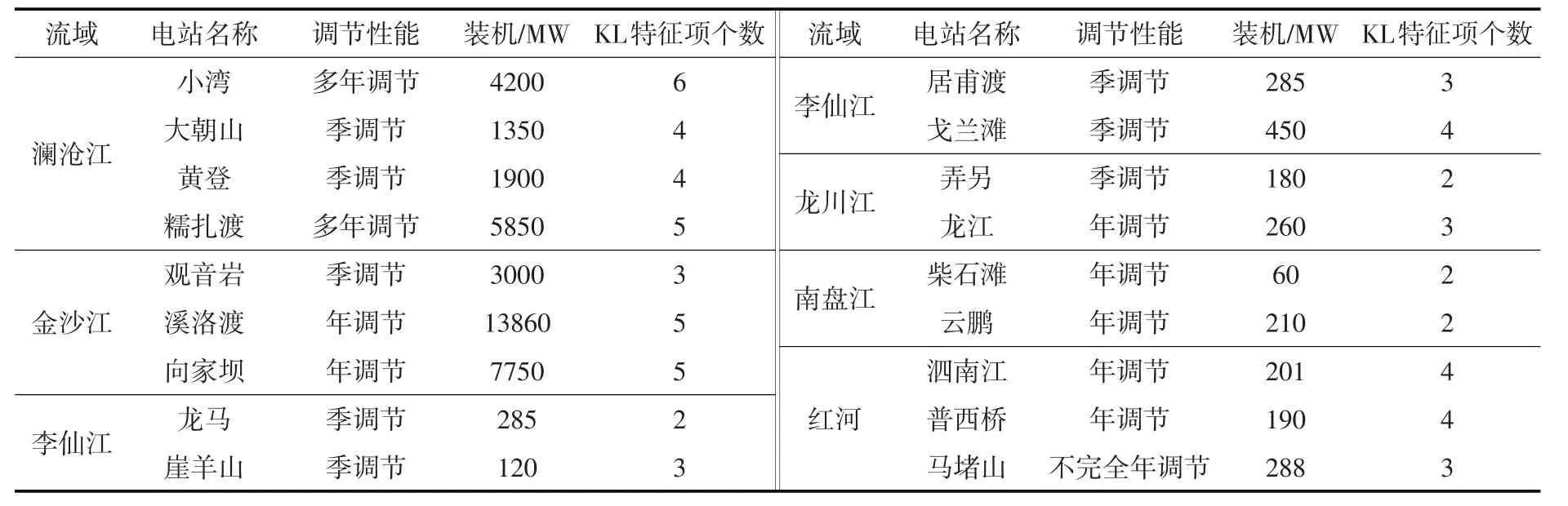
表5 各流域主要调节电站KL特征项个数统计

从表3和表4可以分析，KL 方法在澜沧江、金沙江等大型流域梯级的电量结果优于POA 方法，但在龙川江、南盘江、李仙江等无大型年调节以上电站的主要河流支流，部分来水场景下低于POA方法，主要原因如下。由于澜沧江小湾、糯扎渡水电站具有多年调节性能，调节库容分别达到98.77亿m3与113.35亿m3，因而在不同来水场景下可能存在多种调节调度过程，说明基于调度过程特征的KL方法可以提取到更多有效特征建立KL表达式。以糯扎渡水电站为例，可以提取5个KL特征项，每个特征项对应一种典型调度过程，从而在优化搜索时更精准地给出符合实际来水过程的调度结果。相比而言，龙川江、南盘江等流域电站调节性能较差，可参与优化计算的季调节电站调节库容较小，因此调节调度过程相对偏少，使得KL表达式中包含的有效特征也相对较少（见表4），KL方法优化计算结果的精度相对较低。部分流域历史资料较短，例如李仙江梯级水电站，龙马与居甫渡的资料长度分别为25年与30年，较其余电站50年的历史资料系列偏短，导致调度特征识别的样本集相对偏小，优化得到的电量略少于POA方法。

综上分析，在使用KL方法时，水电站应具有较好的历史调度样本序列和较强的调节性能，这种类型电站进行历史调度特征提取得到的特征项数目通常较多且具有代表性，更易得到较好结果。图3某水电站特征值曲线

4.4 KL方法特征项敏感性分析根据上文分析，KL特征项的选择会直接影响优化计算的结果和效率。为此，本节选择单一水电站和梯级水电站进行特征项的敏感性分析。图3是澜沧江干流某水电站的KL特征值曲线。

根据3.3节中累计贡献率计算方法，该水电站选择了累计贡献率前五的5个特征值及其对应的特征向量用来描述水库调度时段末水位的KL展开式。为了分析特征值选取对于计算结果的影响，分别采用贡献率排序前二的特征值与前三的特征值构建该水电站的KL表达式（简称为KL特征组合1 与KL特征组合2），进行水电站群优化调度计算，结果见图4。

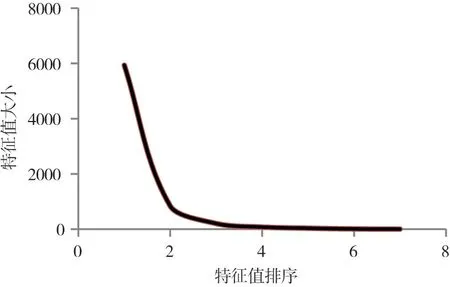
图3 某水电站特征值曲线

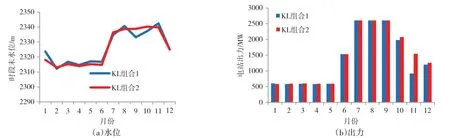
图4 KL特征项组合对比计算结果

从结果可以看出，在采用3个KL特征项构造末水位KL表达式时，电站的调度过程中弃水明显减少，且在汛末及供水期初，电站的发电量有较大增幅，平均每月电量增发幅度达到5%左右。在8—9月中，采用2个KL特征项的调度结果出现了满发情况下仍然放出水量的不合理调度过程，其汛后的发电能力也受到一定影响。而采用3个KL特征项的情况下，电站的调度结果比较合理。因此，按照贡献率排序，特征项个数多的方案，其计算结果更优。该结果从数值实验角度侧面验证了4.3节具有不同特征项的流域梯级调度结果的精度差异。

对于梯级水电站群而言，主要调节电站KL特征项的选择对算法计算效率也存在一定影响。以澜沧江干流梯级4座年调节水电站为例，选择上述4.3节中平水年的来水条件，可以得到不同特征项个数下的计算结果，见表5。

从表6可以看出，主要调节电站的KL特征项选择对梯级总的发电量结果和耗时均有较大影响。随着特征项个数的增加，计算时间随之增加，总发电量也相对增大。以澜沧江干流梯级为例，当小湾、糯扎渡、大朝山、黄登4座电站的特征项均增加1个时，总发电量增加约2.4亿kW·h，计算耗时增加了171 ms。因此，在使用KL方法求解梯级水电站的优化调度问题时，KL特征项的选择是非常重要的，需要结合不同流域梯级的电站特性选择适合的特征项个数，以有效均衡结果精度和计算效率。

表6 不同KL特征项个数下澜沧江梯级电站的计算结果

4.5 随机变量的概率分布分析在使用KL 展开建模时，随机系数概率分布的选取要求满足均值为0、方差为1的条件即可。然而，对于特定物理过程而言，选择不同的概率分布都会直接影响KL方法优化计算的收敛速度和优化结果。上文已经给出了利用Kullback-Leibler 散度选择特定电站随机系数概率分布的方法步骤。本节采用小湾-糯扎渡双库系统进行验证，结果见表7。

表7 电站随机系数适用分布对比计算结果

通过表7可知，对于小湾、糯扎渡两个多年调节水库而言，在多年历史样本情况下，均匀分布对原系数分布拟合最好，损失信息特征最小，故选择均值为0、方差为1的均匀分布作为KL 建模中随机系数的概率分布，以切实反映实际水库调度运行的水位变化规律。为进一步验证其合理性，分别采用3种随机系数分布进行对比分析，通过A、B、C三组分别建立KL展开表达式，对小湾-糯扎渡进行优化调度计算，结果见表8。

表8 不同随机系数分布计算结果对比

可以看出，在可行域内以0.1步长进行搜索计算，A组梯级年发电量最高，说明采用均匀分布进行随机系数组合计算，得到的KL 展开式更符合实际的时段末水位随机过程；B、C 组的收敛时间虽然相对较短，但其随机系数组合相对于均匀分布，对实际随机过程的拟合程度较差，导致优化结果的精度较低。可见，随机系数的概率分布会在很大程度上影响KL方法的收敛速度以及KL展开方程对实际随机调度过程的拟合程度。

5 结论

本文针对超大规模水电系统的高效求解问题，以水电站群长系列实际调度过程数据为基础，耦合KL展开与调度特征提取技术，提出一种大规模水电站群优化调度降维方法，通过云南省调超百座大中型水电站优化调度分析，获得如下结论：（1）在水电优化调度中，采用长系列实际调度过程作为样本，从中提取电站的主要调度特征以实现库水位的准确数学描述，有助于削减模型涉及的变量个数，与经典DP方法相比，在同等计算条件下，其计算复杂度随电站数从指数增长下降至线性增长，能够显著缓解“维数灾”问题；（2）电站调节能力与实际调度过程的数据长短对KL方法的适用性有较大影响。本文实例中，KL方法在实际调度过程资料较长，且年调节及以上电站的优化调度中体现出更好的计算效果；（3）采用KL方法建模时，特征项的随机系数概率分布直接关系到电站水位过程的确定。对于具有长系列调度数据的电站，采用Kullback-Leibler 散度量化评估原始随机过程系数分布与预设分布的信息损失，能够较好地确定随机系数概率分布形式；（4）调度特征项的个数选取对KL方法的结果精度和计算耗时有较大影响，通常情况下，结果精度随特征项个数的增加会得到改善，但计算时间也会随之增加。因此在实际应用中，应结合水电系统的特征选择适合的特征项参数。