谱矩阵试验条件制定方法
2021-03-30吴家驹苏华昌于亮
吴家驹 苏华昌 于亮
谱矩阵试验条件制定方法
吴家驹 苏华昌 于亮
(北京强度环境研究所,北京 100076)
随着多振动台激励系统和多自由度控制系统设备能力的发展,六自由度随机振动试验方法已被纳入美军标。本文专注于研究多自由度试验系统输入条件的确定,指出两个自由度之间振动的相干度是非常重要的参数,相干为零的独立基础激励未必反映最严重工况,提出了一个广义的六自由度振动条件的制定方法。利用滑动平均将实测信号分解成平稳载波和时变调制波,然后多个载波信号被整合成一个时间序列,通过时平均得到归一化的六自由度参考谱矩阵。虚拟仿真试验结果证明了方法的保真度。
谱密度矩阵;多振动台试验;厄米特矩阵;乔列斯基分解;保真度
0 引言
多维振动试验技术广泛地应用于军用设备的研制,多振动台试验方法已被纳入通用的试验室规范。六自由度随机振动试验,在我国已成功应用于惯性测量组合的研制试验,为解决隔振与捷联的矛盾和导航精度的射前评估提供了环境模拟手段[1]。在最近几年,六自由度电磁振动台的出现标志着实现真实多自由度随机振动试验能力的巨大突破[2]。军用设备环境试验方法标准更是从真实再现使用环境的角度,将原来的多振动台试验方法,规范为六自由度随机振动试验方法[3]。
图1说明了实施六自由度随机振动试验需要三个要素:振动台系统、控制系统和环境的规定[4]。前两个要素主要是涉及硬件,由于采用了“冗余结构”的概念,使得六自由度振动环境的物理试验成为可能。第三个要素是短板,主要在于有关外场环境的表征、测量和试验条件制定方法还未规范,因为六自由度试验包含比传统单自由度试验更多的环境信息,尤其是还涉及运动自由度之间的关联程度。
最近发布的美军标规定,用功率谱密度矩阵来表征六自由度随机振动环境,用相干函数来表征运动自由度间信息关联程度,认为低相干度会给出保守的结果[5]。标准建议只对矩阵的下三角部分作统计包络处理,然后共轭复制上三角部分,形成试验条件。方法保证了谱矩阵的正定性,同时自谱的包络也会获得保守的条件。可是对作为复数的互谱实行包络操作的正当性,尤其是独立即保守的论断缺乏理论上的依据。

图1 六自由度振动试验文氏图
本文拟通过数值模拟方法,解释相干函数的物理意义。探索运动激励之间的相干与力激励之间的相干和被试结构动力学特征的关联程度,相干为零的独立激励是否一定产生最严重的响应。在得出与之不同的结论后,提出了如何从实测信号中获得更多相干相位信息的算法,以制定出合理的试验条件。首先将外场试验测量的多路随机时间历程,分解成反映振动烈度的调制波和单位高斯分布平稳载波[6],然后用不同方法分开处理。前者按对数正态分布统计,形成时间窗函数。后者整合成的长程时间序列估计出归一化谱矩阵,与时间窗函数一起成为六自由度参考谱矩阵。为了叙述方便,将标准建议的方法称之为“相平均法”,这里介绍的方法称之为“时平均法”。
为了验证方法的合理性,设计了一个车载导弹运输振动简化模型进行虚拟试验,用蒙特卡洛法模拟多工况外场试验和室内试验,以计算应力估计的累积损伤作为判据,对两种方法的效果做出定性比较。
1 参考谱密度矩阵分解
运载器在运动过程中受外力(风、噪声和路面不平等)激励,通过安装界面传递给设备,使之产生空间随机振动,界面运动(加速度)的大小反映出外界激励(力)的大小。多自由度振动试验条件通常用频域的谱密度矩阵来表征,其对角线项是自谱,反映了各自由度自身振动烈度,非对角线项是互谱,反映各自由度之间的时差(相位)和因果(相干)关系。试验模拟自由度数的选择取决于对振源的了解和室内试验模拟能力,随着数据处理硬件软件的发展和先进控制策略的应用,商品化的振动控制仪已经能够实现基于谱矩阵的高斯随机振动试验控制。
根据运动控制试验原理,模拟了安装界面的运动等同于模拟了界面力[7],这样试验条件制定问题就变成如何表征界面运动。传统的单自由度试验,基于设备的尺度和体积远小于运载器的假设,将安装界面的运动简化成一个质点的运动。而基于多振动台激励的三轴振动试验,虽然模拟外场使用环境能力明显提升,但仍然没有脱离质点运动的假设。经过多年实践摸索,业界目前更倾向于通过六自由度试验来模拟军用设备的使用环境。六自由度试验基于平剖面假设,即安装界面运动可以用刚体沿三正交轴的平移和绕三正交轴的转动来表征。这个假设显然受频率范围的限制,因为在试验频率内安装界面存在弹性模态时,就需要更多自由度来表征。代表多自由度振动试验条件的参考谱密度矩阵,通常有两种生成方法。一种是根据外场试验所测量的多路时间历程通过谱分析统计形成[5]。另一种是从数据库中获得自谱,互谱则通过研究某些临界响应的所谓最小驱动方法得到[8]。两种方法给出的参考谱矩阵都必须与控制仪控制算法匹配。
现代控制仪多用基于周期图的韦尔奇方法进行谱估计,用“逆韦尔奇”方法随机化。试验模拟的关键是要保证参考谱矩阵对每一个频率都能实现乔列斯基分解,即在数学上需要矩阵满足正定条件。以二自由度为例,谱密度矩阵可写成
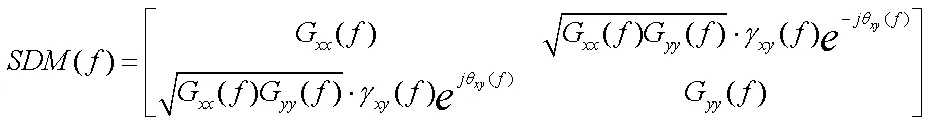

对于用单次测量时域信号变换形成的谱矩阵可以满足正定性,但通常试验条件不能仅凭一次测量确定,还需要通过统计多次测量以预测最恶劣环境。制定试验条件过程中的数据处理操作,包括考虑各种工况量级的统计包络、预计经历时间长短所做的时间压缩等会破坏矩阵的正定性。另外,为了降低界面弹性模态影响,还需要采用冗余测量方法,通过传递矩阵的伪逆,来获得反映安装界面刚体运动的六自由度谱密度矩阵,也会使得某些频率不能满足正定条件。为保证参考谱密度矩阵是厄米特阵,文献[5]建议采用谱密度矩阵的下三角部分或乔列斯基分解后的下三角阵进行加权统计平均(相平均),然后共轭复制上三角部分,并且基于“独立是保守的”论断,将出现小相干函数值的频带视作零相干,以此来简化参考谱型。该方法能维持矩阵正定性,但其结果的保守性值需进一步研究。下面通过数值计算,来论证零相干的独立激励未必产生极值响应,并研究如何处理相干函数,才能使参考谱矩阵正定且结果保守。
2 相干函数影响分析



或者
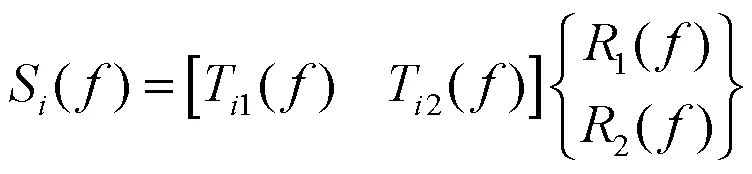

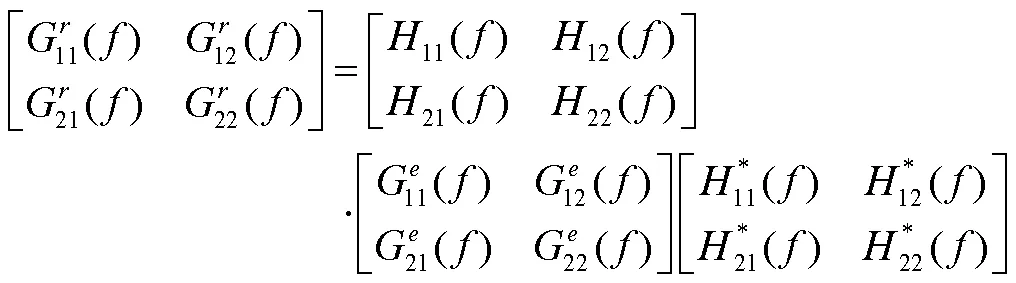
左端项代表外场测量数据估计的响应谱矩阵,其对角线项包含的相干函数与系统的频响特征和激励矩阵关联,其解析形式比较复杂,推导过程繁琐。
本文拟通过数值分析方法,定性地解释相干函数的物理意义。频域乘积可转化为时域的卷积,因此响应的时间历程可表示为

将图2的模型进一步简化,用一根刚性梁两点弹性支撑的二自由度系统表示,以便进行两种简化梁的数值计算仿真。首先设定振源为独立白噪声,激励谱密度矩阵为单位阵,即互谱为零,自谱为1进行仿真。图3给出二自由度系统(刚性梁)响应相干随频率变化(较高位置)曲线,图中还给出了系统的频响交联项(较低位置)。可以看出,在低频相干度接近于1,仅在(跨点)频响的谷值处出现低值(约为0.1)。图4给出弹性梁(多自由度系统)的响应相干随频率变化曲线。可以看出,在(跨点)频响谷值频带内出现低的相干度,具体位置与此频带内的反共振谷深度有关。图3和图4说明响应相干与系统的动力学特征有关。其次设定激励谱密度矩阵为对角阵,但自谱量级不同进行仿真。按相同方法分析结果见图5。可以看出,自谱量级变化会改变出现最小相干函数值的频率。最后,设定两个激励的自谱密度相同但相干不同进行仿真,按相同方法分析结果见图6。可以看出,响应相干函数值与激励相干函数值相应变化趋势相同。不过,响应相干出现最低值的频率也发生变化,而且即使是全相干激励,在某些频率响应的相干函数也不为1。
通过数值仿真分析可以看到,外场测量数据本质上是载体在外力作用下的运动响应。各个测量自由度之间的相干与相位,自然与外力之间的相对烈度和相干有关,也与振动系统固有特征有关。自谱的大小反映振动的烈度,可以通过提高自谱的量级来增加试验的保守性。但是相干函数能否给出一个保守性的指标,还需要深入探讨。

图3 二自由度系统响应相干函数

图4 多自由度系统响应相干函数

图5 相干函数随激励量级比变化
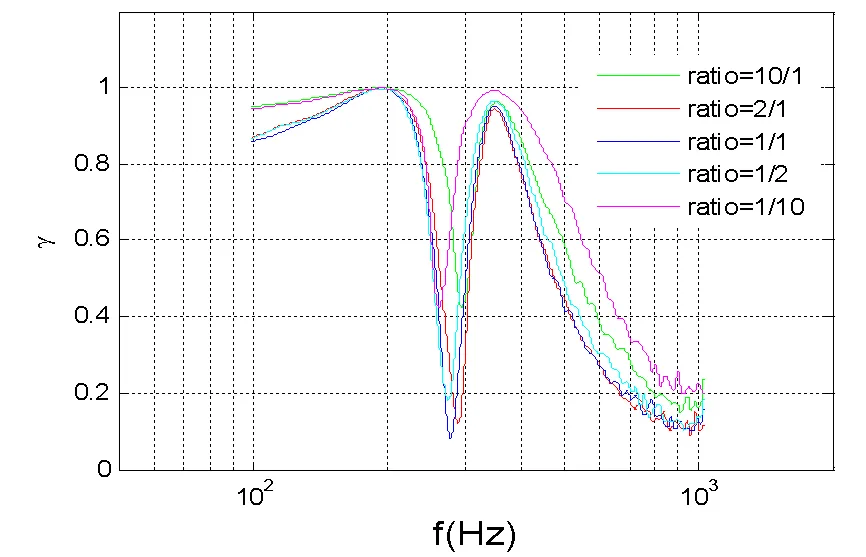
图6 相干函数随激励相干变化
进一步分析输入信号之间相位关系对输出的影响,有助于外场真实环境的模拟。仍以二自由度模型为例,回到(9)式



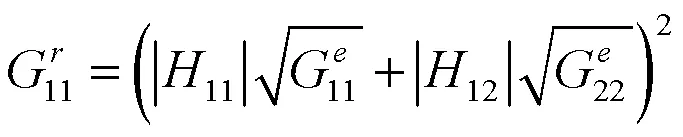

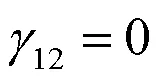
3 谱矩阵估计的相平均法

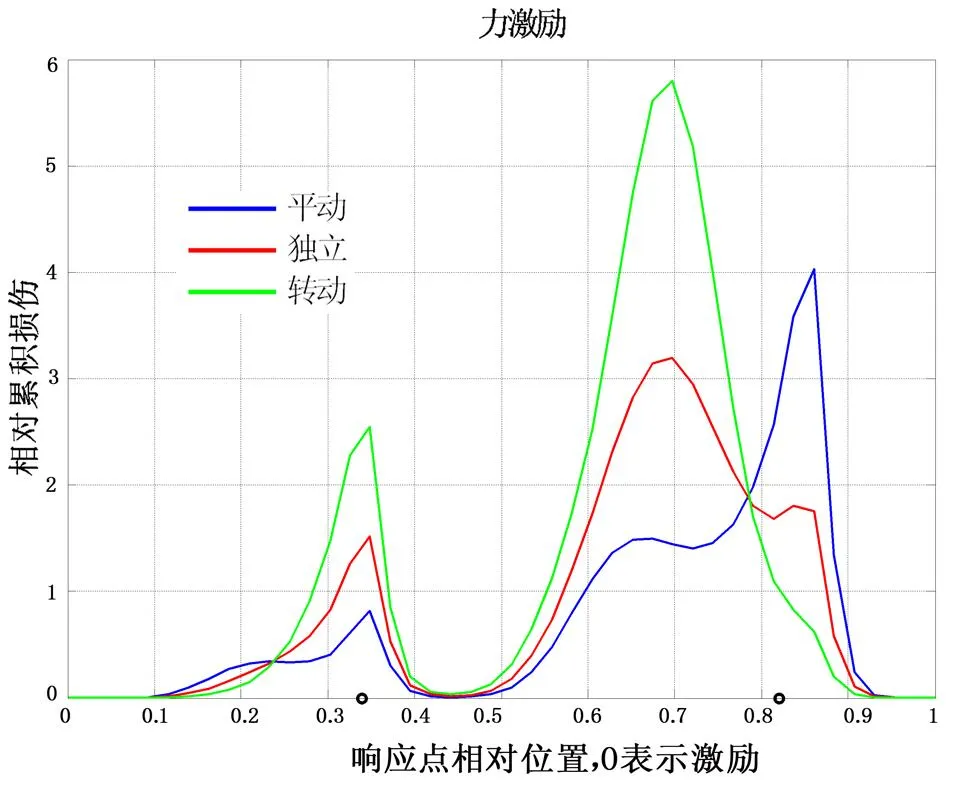
图7 输入相干效果(力激励)
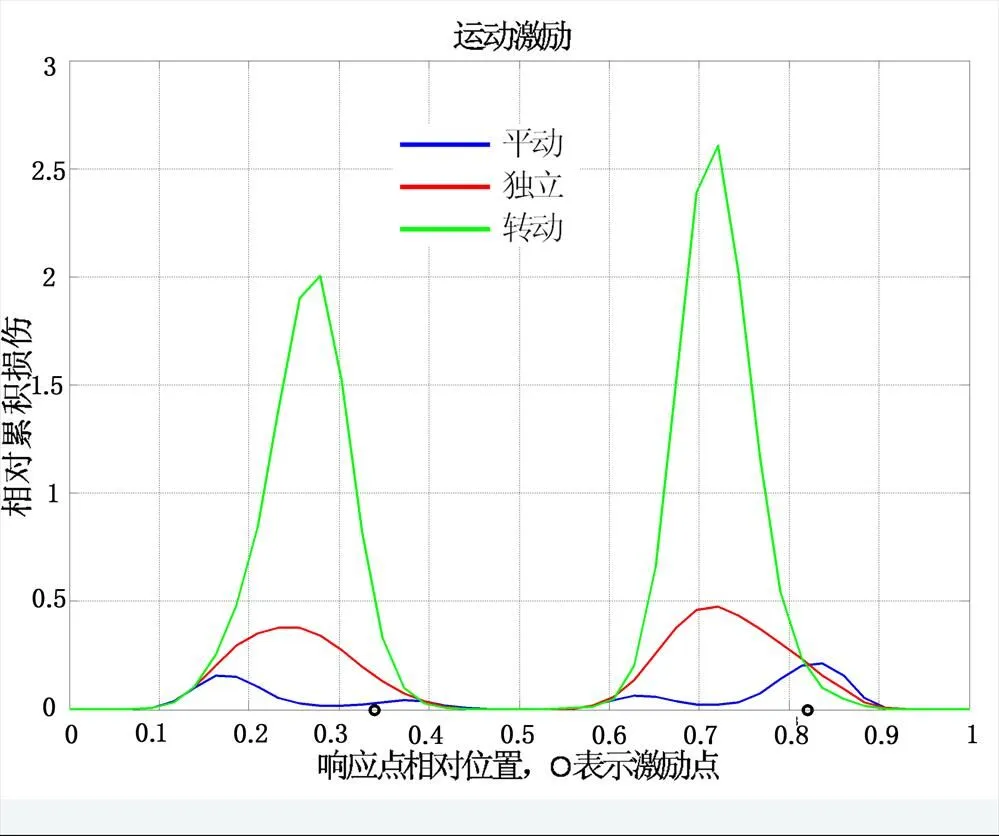
图8 输入相干效果(运动激励)

图9 相平均制定试验条件流程
这里的“上限包络”指的是,多次测量得到的谱矩阵是变化的,对每一个频率计算谱矩阵的每一个元素的均值和方差,并按一定的分布(例如对数正态分布),估计最严重环境,作为试验条件。可是互谱是复数,实部和虚部有正有负,不会与自谱有相同的分布。实践证明互谱的平均结果是趋于降低相干度。虽然互谱还能用极坐标表示(模和相位),但是由于周期性缠绕,对相位进行求均值运算会得出不正确的结果。通过以上分析发现,相平均方法的保真度可能存在问题。既然运动激励的相干和相位对响应有明显影响,那么就有必要在确定参考谱矩阵时,尽量维持原有的互谱属性。为了实现这一目的,本文采用区别对待矩阵对角线项和非对角线项的制定试验条件方法。
4 谱矩阵估计的时平均法
首先将外场测量的多路随机时间序列,逐一分解成一个窗函数(调制波)和单位方差的高斯分布随机序列(载波),然后用不同的方法统计处理[6]。对于一次测量


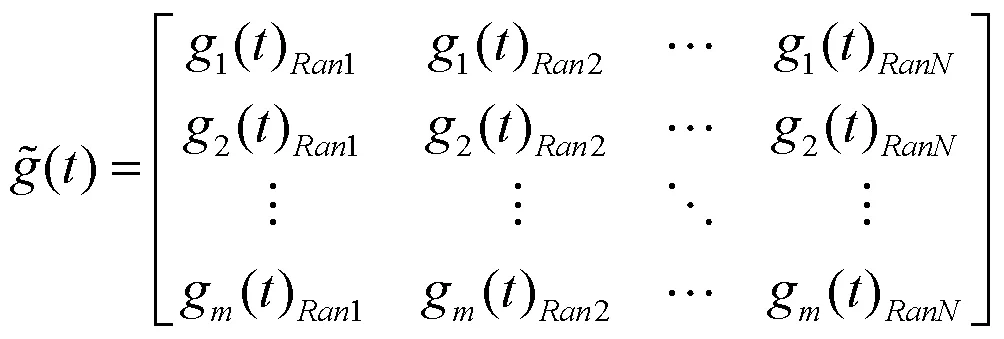




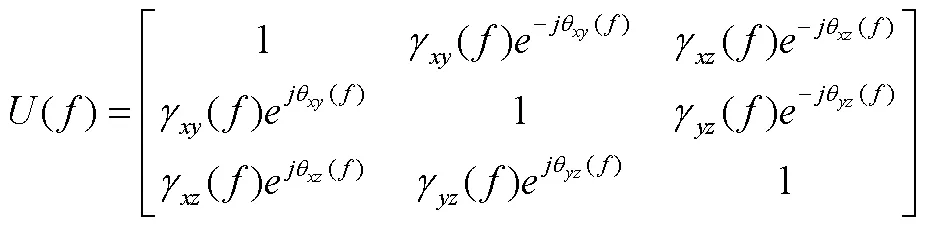

5 虚拟仿真试验
为了研究方法的保真度,继续利用简化版的车载导弹运输振动模型,进行两点激励的均匀梁虚拟试验,用蒙特卡洛法模拟多工况外场试验和室内试验,以计算应力估计的累积损伤作为判据,对不同方法的效果做出定性比较。

一共完成了九次试验,每一次先产生烈度(均方根值)随机设置的相互独立的白噪声,作为梁的外激励力。计算两个激励的加速度响应时间历程,模拟一个工况的外场测量,作为制定参考谱密度矩阵的一个子样;同时计算出梁的应力时间历程,并估计所造成的累积损伤。然后,用九个工况激励点的加速度时间历程,分别按相平均法和时平均法形成参考谱密度矩阵。最后,用两个谱密度矩阵,反演成两路加速度时间历程,作为基础激励,计算梁的应力响应时间历程和所造成的累积损伤。室内试验模拟也进行了九次。

图10 时平均制定试验条件流程

图11 虚拟试验流程
图12展现出虚拟试验的相对累积损伤。最浅颜色曲线表示九次实测振动激励造成的累积损伤的上限极值。最高位置曲线和最低位置曲线分别表示基于九次实测振动,用时平均法和相平均法得到参考谱矩阵激励造成的累积损伤的预测值下限。
可以看到,两种方法相比,时平均法的预测效果更接近外场环境,而且偏于保守。相平均法的预测效果偏离外场环境,特别是会造成“欠”试验,原因可用图13来说明,图13是运动激励的参考谱矩阵。
两者自谱的全频段几乎一样,两者的相干和相位仅在300~500Hz带内一致,其余频带差别较大,且相位基本反相。
时平均法得到的相干很高,相平均法所得到的相干却很低,而低相干趋于独立的运动激励的结果不是保守的。
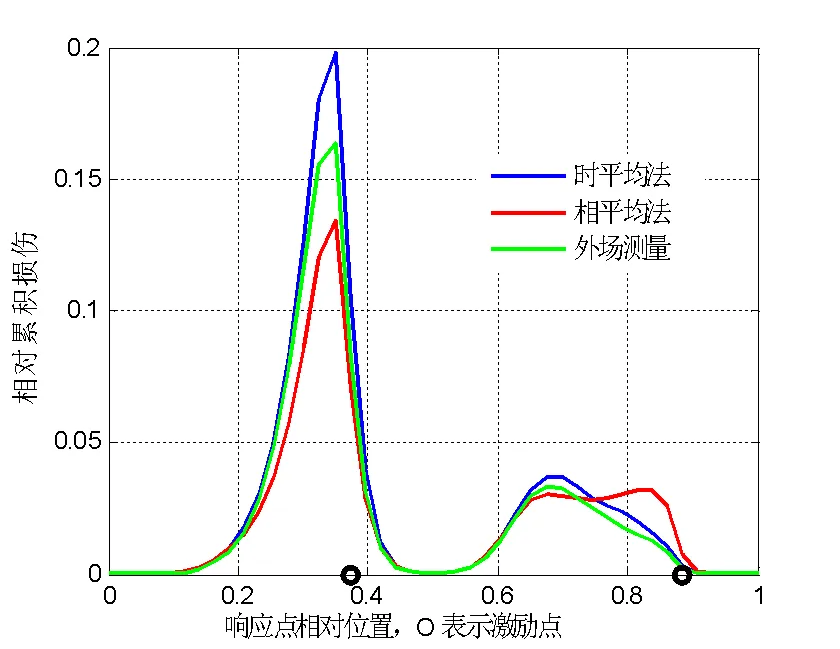
图12 累积损伤结果比较
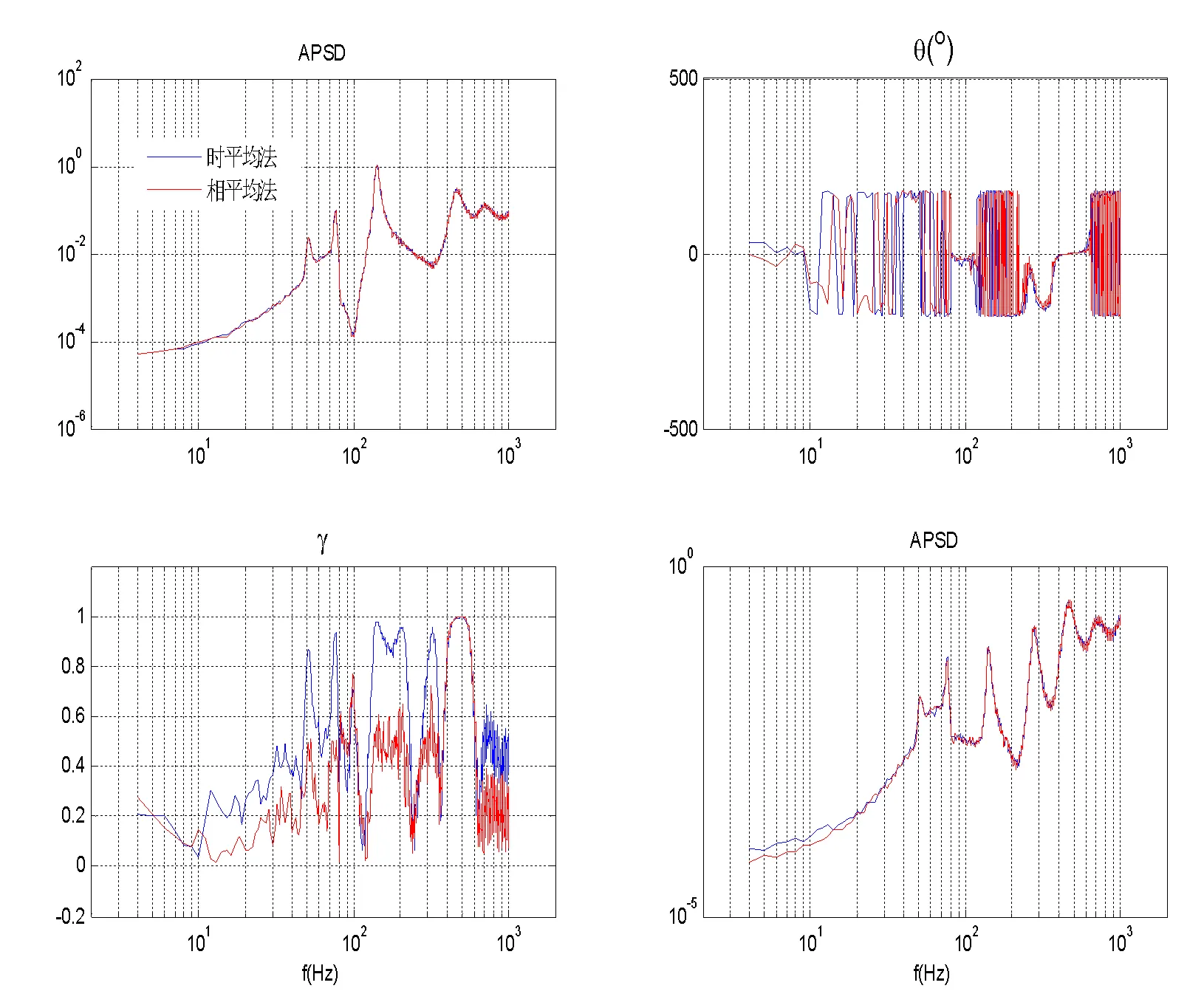
图13 参考谱矩阵比较
6 结论
随着振动台和控制仪的进步,六自由度随机振动试验已经标准化,一个新的参数-谱矩阵被用来表征多维随机振动环境,试验条件的制定迎来了新挑战。传统基于实测外场测量的(自)谱密度统计方法,是否适用相干相位的统计处理,是一个需要讨论的问题。
通过数值分析表明,制定试验条件的外场测量数据本质上是载体在外力作用下的运动响应,各个测量自由度之间的相干相位,与外力之间的相对烈度和相干有关,也与振动系统的固有特征有关。由于相干与试验保守性之间没有烈度那样的相随关系,依据外场测量数据制定谱矩阵规范时,应当尽可能保留特定工况下的相干特征。从这个意义上讲,谱矩阵条件只能是“量身定做”,不能成为“货架产品”。军用规范推荐的相平均方法趋向于产生独立的谱矩阵试验条件,但独立运动激励未必产生保守的响应。本文提出的实测信号分解→整合单位高斯载波→通过时平均得到归一化参考谱矩阵的方法,有效地保留自由度之间相干特征。基于两点激励的车载导弹运输振动简化模型仿真结果表明,该方法既模拟了外场环境又能做到适度保守。虽然该方法通过了虚拟试验演示验证,但仍需要更多的六自由度外场测量和物理试验来证明,尤期需要建议一个有效评价体系,相关问题会在后续的文章中讨论。
[1] 吴家驹, 等.用于惯性测量组合的金属减震器[R].航天报告, 2002(2): 1-5.
[2] Hoksbergen J.Bringing broadband 6-DOF field vibration environments into the lab-tensor 18kN vibration test system [J].Sound & Vibration, Dynamic Testing, March, 2013.
[3] MIL-STD-810H .Multi Exciter Test, Method 527[S].
[4] Maitin L, Schctral S.On the nature of spectral density matrices used to the characterize vibration environments[C].Proceedings of the 87thShock & Vibration Symposium.
[5] Hale M.Spectral density matrix transformation[J].Journal of the IEST, 2017, 60(1):17-26.
[6] 吴家驹, 付玮, 张鹏飞.基于β分布随机数排序的非高斯振动模拟方法[J].强度与环境, 2017, 44(2): 10-16.[Wu Jiaju, Fu Wei, Zhang Pengfei.Simulation method of non-Gaussian vibration base on re-arrangement of β distribution random number [J].Structure & Environment Engineering, 2017, 44(2): 10-16.]
[7] 吴家驹, 荣克林.多维振动环境试验方法[J].导弹与航天运载技术, 2003(4): 27-32.[Wu Jiaju, Rong Kelin.Multi-dimentional vibration environmental test method[J].Missiles and Space Vehicles, 2003(4): 27-32.]
[8] Smallwood D O.Extreme input/outputs for multiple input multiple outputs linear systems[S].SANDE 2005-5307.
[9] Smallwood D O.Multiple shaker random vibration control an update PIES[S].1999.
[10] 吴家驹, 丁镇军, 丁富海.非高斯多维随机振动分析[J].强度与环境, 2018, 45(4): 1-6.[Wu Jiaju, Ding Zhenjun, Ding Fuhai.Analysis of non-Gaussian multi-random vibration [J].Structure & environment engineering,2018, 45(4): 1-6.]
[11] Sandia National Laboratories.Sandia’s new vibration table promises different ways of testing[S].2015.
[12] NASA-HDBK-7005.Dynamic environmental criteria [S].2001.
On the Derivation method of Spectral Density Matrix Specifications
WU Jia-ju SU Hua-chang YU liang
(Beijing Institute of Structure and Environment Engineering, Beijing 100076, China)
With the development of multiple excitation systems and MDOF vibration control systems, the 6-DOF laboratories vibration test method is brought into MIL-STD.This paper concentrates on the determination of an input specification for such MDOF systems.It is pointed out that the coherent value between two degrees of freedom is a very important parameter.The motion excitation of independent foundation with zero coherence does not necessarily reflect the most serious condition.A generalized 6-DOF vibration specification development technique is proposed.The measured signal is decomposed to the stationary carrier and time-varying modulated wave by the moving average.Then, a lot of carrier is integrated into a time series.The normalized 6-DOF spectral density matrix is obtained by time averaging.Virtual simulation results demonstrate the fidelity of this method.
Spectral Density Matrix (SDM);Multiple-Exciter Test(MET); Hermitian Matrix; Chlesky Decompose; Fidelity
V416.2
A
1006-3919(2021)06-0050-09
10.19447/j.cnki.11-1773/v.2021.06.008
2021-06-29;
2021-09-15
吴家驹(1939-),男,研究员,研究方向:随机振动分析与试验;(100076)北京9200信箱72分箱.
