一种基于无线传感器网络的动态环境自适应定位方法

杨文铂,刘彦华,3,崔明月

(1.河南工业职业技术学院 电子信息工程学院,河南 南阳 473000)(2.南阳师范学院 物理与电子工程学院,河南 南阳 473061)(3.河南省工业嵌入式网络控制工程技术研究中心,河南 南阳 473000)

当前在室外开放环境下的基于卫星导航的定位、路径规划、地图建立等技术经过长期的研究已经基本成熟;但用于矿井、室内、隧道等复杂、封闭、不确定环境中的定位技术由于多径效应、非视距传输和温湿度变化等条件的影响,还需要进行更深入的研究[1]. 在各种应用中,位置信息非常重要[2],近年来随着无线传感器网络(WSN)广泛应用,利用其构建定位网络成较好的方案. 基于WSN的定位技术因其不依赖于GPS等外部系统,适于室内外等多种复杂环境,成为当前研究热点. 常用的WSN的静态定位算法有加权质心算法(WCLA)[3]、加权最小二乘估计算法(WLSE)等[4]. 为了提高定精度,WCLA和WLSE等都需要供与参考节点间的距离作为权值,这两者属于距离相关定位算法[5]. 距离的获取可通过TDOA、TOA、AOA以及RSSI等方式取得. 其中TDOA、TOA是基于到达时间测量,AOA是基于到达角度测量[6]. 加州大学洛杉矶分校的Andreas Savvides等人设计了一种称为“Medusa”的无线传感器节点试验平台(配备有射程3m的超声波收发器,可使用TDOA技术以2cm的精度测量距离),并在该平台上开发了AHLos和n-hop multilateration primitive定位算法.AHLos 系统则采用了 TDOA+极大似然估计,并将已定位的节点升级为锚节点来缓解锚节点较少的问题,但会造成误差累积[7]. TDOA、TOA、AOA等定位方法需要添加额外的超声波、天线阵列等硬件,会增加WSN系统的成本、功耗和复杂性.

RSSI是基于信号强度指示,利用无线信号强度随距离衰减的特性进行测距[8]. 在WSN中,RSSI可直接从接收信号中提取,而不需要添加额外传感器,并且简单、低成本,因而成为WSN定位技术的研究热点. 微软的 RADAR 系统是较早使用基于RSSI指纹识别的定位系统,利用信号强度估算距离,采用匹配数据的方法定位,考虑了环境因素,需要大量的离线训练数据,且对于不同的环境需要重新采集数据,成本较高[9]. 苹果公司采用iBeacon技术,通过Measured Power和RSSI值计算接收机和iBeacon中间距离,用户的位置可以被精确定位至几英尺的范围内[10]. 现有的基于RSSI的定位算法大多需要预先获取环境参数,这对于复杂和不确定的定位环境如矿井、室内、隧道等是不现实的. 由于环境的不确定性,此类算法必然会导致较大的定位误差.

本文深入研究了现有的WSN定位技术,针对复杂不确定性定位环境,首先提出了基于RSSI的环境自适应测距算法(EAR),及其衍生的静态自适应定位算法(EAR-WLSE),利用极大似然法拟合自适应辨识出定位模型中的未知环境参数,实现定位算法的环境自适应,大大提高了在复杂不确定环境下的定位精度和适应性. 然后在此基础上利用当前统计模型-扩展卡尔曼滤波算法(CS-EKF)降低信道噪声和动态过程误差,提出了动态环境自适应定位算法(DEAP). 相比于现有的算法,本文算法可适应复杂定位环境并有效提高探测精度. 经定位实验和仿真证明,该方法相比WCLA、WLSE等传统定位方法具备更高的定位精度,具备普遍应用意义.

1 基于RSSI测距的静态环境自适应定位算法(EAR-WLSE)

1.1 RSSI-距离模型特性

基于距离的定位算法,距离获取精度很大程度上决定了定位精度. WSN中采用RSSI测距方法可以直接从网络信号中提取距离信息,最为方便、成本低. RSSI是利用无线信号随距离衰减的特性进行测距. 通常用对数-常态模型(Shadowing)描述RSSI-距离衰减特性[11],有公式给出:

PL(d)=PL(d0)-10Nlgd/d0+Xs.

(1)

式中,d为接收端到信源的距离,d0为参考距离,PL(d)为接收信号强度(单位dBm),PL(d0)为在参考距离的信号强度,N为传播系数,反映信号随距离的衰减速率,Xs为均值为零的信道白噪声,在上述模型中PL(d0)和N参数都要通过实测确定. 通常取参考距离d0为1 m处的信号强度值PL(1),此值记为常数A[12],所以式(1)可变换为如下形式:

PL(d)=A-10Nlgd/d0+Xs.

(2)

在复杂信号环境中,由于多径传播、障碍物、温湿度等环境因素导致局域无线电传播参数变化的情况是普遍存在的,而Shadowing经验公式中使用固定的传播参数,必然会导致较大的定位误差. 为了实现定位算法的环境自适应,则必须根据不同的局域定位环境辨识出对应的RSSI-距离模型,辨识过程必须是动态、实时进行,以尽可能降低测距误差.

1.2 环境自适应测距模型辨识

定位环境设定:待定位平台上安装有定位节点,定位区域设置有若干参考节点,定位节点和参考节点处于同一个WSN中,参考节点坐标已知,并向WSN中定期广播自身坐标信号. 记RN为定位节点接收到第N个参考节点的信号RSSI值,此信号中可提取出参考节点的坐标(XRN,YRN). 首先建立以RN为自变量的m次函数Y(RN),代表定位节点与参考节点的距离.

(3)

将N个当前定位节点位置到参考节点的距离公式联立得:

(4)

为了获得Y(RN)中的系数,可在定位节点处于某个已知位置上时采集相邻参考节点的信号. 此时定位节点与相邻参考节点的真实距离yN是确定的,由式(5)给出.

(5)

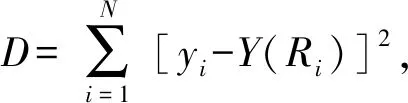
根据Friis模型[16]:

Prcv(d)=Prcv(d0)·(d0/d)λ=C·(1/d)λ,

式中,Prcv为接收能量,d0为标准距离,λ为衰减系数,取环境均值,对距离求导得

得

ΔPrcv≈-C·λ·(d)-λ-1·Δd.

在相同信道噪声下,距离的误差可表示为:

测量方差

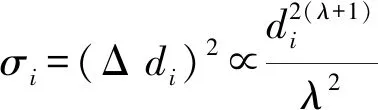
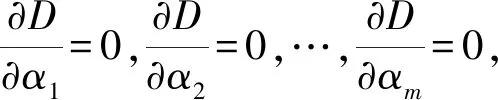
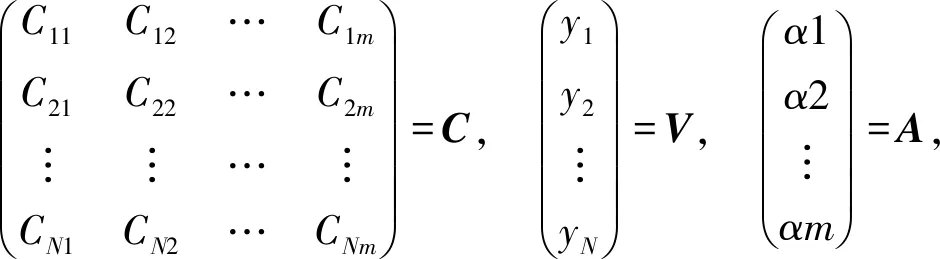
式中,Cij是由Ri计算而得到,则

得

1.3 静态环境自适应定位算法(EAR-WLSE)

前文通过EAR算法对不确定环境下节点间距离进行精确求解,并研究了无线信道特性,对噪声对测距误差的影响进行了深入分析,得到了适用于异方差距离特性下的权值矩阵W. 而在WLSE算法中仅简单使用距离倒数作为权值,不够准确,如果将改进的权值矩阵W引入WLSE中,可以实现近似的无偏估计,将有效提升定位精度,在EAR测距模型的基础上得到静态环境自适应-极大似然估计定位算法(EAR-WLSE). 设有N个参考节点ref1(xb1,yb1),ref2(xb2,yb2),…,refN(xbN,ybN).d1,d2,…,dN分别为定位节点到各参考节点的距离. 根据距离关系有:

解得:X=(ATWA)-1AWB.

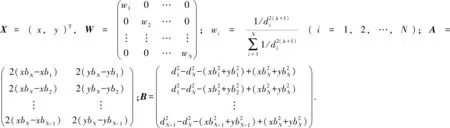
2 改进的动态环境自适应定位算法(DEAP)

受不确定环境下多径传播、随机信道干扰及定位平台移动导致的时延等因素影响,会产生定位过程噪声,导致附加的定位误差. 在EAR-WLSE算法的基础上引入扩展卡尔曼滤波(EKF)方法对目标进行跟踪,可有效抑制过程噪声、提高定位的精度和动态响应特性. 定位平台在移动过程中会有部分匀速运动过程,受外界的影响会有变速运动以及转向运动,因此,定位平台具有一定的变加速特性[17]. 目前,描述机动目标的模型有CV模型、Singer 模型等,当前统计模型(CS Model)采用时变加速度概率密度函数与加速度非零均值-时间相关模型,因而可以更好地描述定位平台的运动特性. 本文采用当前统计模型作为状态方程、坐标估计值为观测量[18]. 首先基于EAR-WLSE静态定位算法计算出坐标估计值,然后使用当前统计模型扩展卡尔曼滤波方法(CS-EKF)修正定位坐标,得到动态自适应定位算法(dynamic environmental adapted positioning algorithm),以下简记为DEAP算法.

2.1 状态方程

目标在二维平面上做变速运动,以目标运动状态Xt=(ZtVtat)T作为状态向量,其中Zt,Vt,at分别是位置、速度和加速度,得到运动目标的离散动态模型[19]:

Xk=AXk-1+ΓWk-1

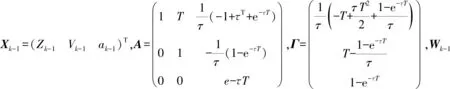
2.2 观测方程

将改进自适应定位算法检测到的目标节点的坐标值作为观测量Z(k)=(X(k),Y(k))T观测方程:

Z(k)=HX+v(k).

H为状态向量X(k)到Z(k)的雅克比矩阵,v(k)为观测噪声.

时间更新方程:

Q为过程噪声协方差矩阵,测量更新方程:

Zk=α0+α1r+α2r2+…+αmrm,

2.3 测量噪声协方差矩阵的确定

根据EKF过程,状态向量的最优估计受到过程噪声和测量噪声的影响,噪声协方差矩阵会影响跟踪定位的精确性[20]. 根据前面的分析,距离误差由RSSI测量噪声造成,RSSI测量噪声可根据高斯滤波方法测量得到[21]. 由于vk(rssi)～N(0,Rrssi),噪声的协方差为COV[vk(rssi)]=Rrssi.可得测量噪声的协方差矩阵为:

Rv=COV[vk]=COV[Wvk(rssi)]=WRrssiWT.

3 DEAP算法流程设计

在DEAP算法工作时,需要进行动态定位参数辨识,得到当前环境下的测距模型参数并置于自适应定位模型中. 在参数标定之后才能进行连续定位,否则会导致较大的测距误差. 参数标定方法是当定位节点位于或靠近已知坐标点时,收集周围参考节点定位信号,运行EAR中的环境自适应测距模型参数辨识程序得到无线电传播参数.

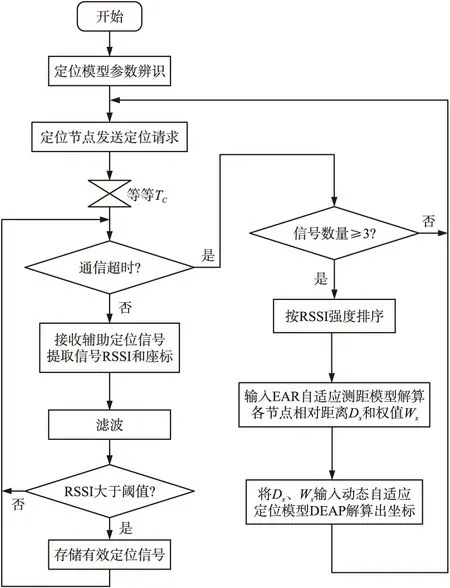
图1 算法流程Fig.1 Algorithm procedure

参数标定完成后,定位节点定期向网络中广播定位请求并等待一个固定的收集周期Tc,在此周期内参考节点会向网络中定期发送辅助定位信号,此信号中带有当前参考节点的位置坐标. 定位节点在Tc内收各集参考节点的信号,首先提取其有效RSSI值和参考点坐标,并存储起来. RSSI值需大于阈值,否则为无效信号. 在Tc内如果收到多于3个有效定位信号即启动定位算法;否则视为通信超时,重发定位请求. 定位节点首先对定位参考信号按RSSI值进行降序排序,然后提取出信号中参考坐标值,在滤波过程中如果某个RSSI值呈现出非距离相关特性,则将其剔除. 将序列的RSSI信号集输入自适应测距模型EAR,解算出其相对于定位节点的距离. 对所有参考节点执行同样的测距计算,得到各点的相对距离Dx,根据Dx解算出距离权值Wx,将各参考点的坐标值Cx,相对距离Dx、和距离权值Wx代入动态自适应定位算法模型DEAP,解算出定位坐标Cb,完整定位算法流程如图1所示.

4 结果与讨论

4.1 静态环境自适应定位算法(EAR-WLSE)验证

为验证自适应测距算法(EAR),选取了最小二乘拟合(LS)和加权最小二乘拟合(WLS)算法作对照,选取5组室内外环境实测数据,按照各自算法分别进行数据拟合得到传播特性曲线. 测试中,参考节点和移动定位节点使用满足IEEE 802.15.4协议的CC2530模块[22],采用10 dBi的2.4 GHz鞭状天线.

移动定位节点采用履带式移动机器人平台,装有夜视功能的云台摄像头,用Android终端遥控,便于在室内复杂环境下控制,定位测试平台如图2所示. 为验证自适应测距算法,参考节点在固定位置连续发送定位信号,移动定位节点接收并提取RSSI值,每隔1 m相对距离采集一组RSSI-距离数据,每组连续采集20次取平均. 图3是在实际室内环境1(23 ℃,40%RH)下,得到的各测距模型的传播特性曲线,ENV为真实环境RSSI-距离传播特性曲线,EAR对真实环境特性的拟合精度最高. 接着选取了5种不同环境条件(EV1-EV5)下的平均测距误差作对比,如图4所示. EAR采用三次拟合,LS 的平均测距误差为1.9 M,WLS 为 1.3 M,EAR 为0.11M. 如图4所示,EAR具有最高的测距精度,而且无需事先标定传播参数,可实现环境自适应. 为了验证静态定位算法EAR-WLSE,选取了最小二乘估计(LSE)、加权最小二乘估计(WLSE)和加权质心算法(WCLA)作对照,采用Monte Carlo-100仿真,设定位区域内参考节点均匀分布,无线电传播参数A在36 dBm上下20%范围内随机浮动,传播参数N取2至6内随机值. 最小二乘估计法、加权最小二乘估计及加权质心算法采用经验模型测距(见式(2)),A参数使用不变值-36,N取平均值4. EAR-WLSE采用EAR算法进行测距. 从图5可以看到,定位精度与参考节点数量呈正相关关系. 首先,WLSE定位精度比LSE有显著提高,显示出距离权值在提高定位精度中的作用,随后引入了环境自适应的EAR-WLSE算法平均定位误差比WCLA降低了35%以上,比WLSE降低了45%以上,表明引入的自适应算法在提高定位精度上的显著作用. 测试结果显示:在不确定性信号传播特性环境中,上述算法中EAR-WLSE具备最优的定位性能.

图2 定位测试平台Fig.2 Positioning test platform

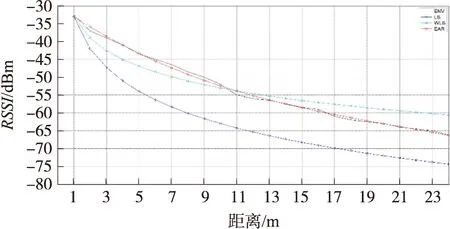
图3 拟合曲线对比Fig.3 Fitting curve comparison

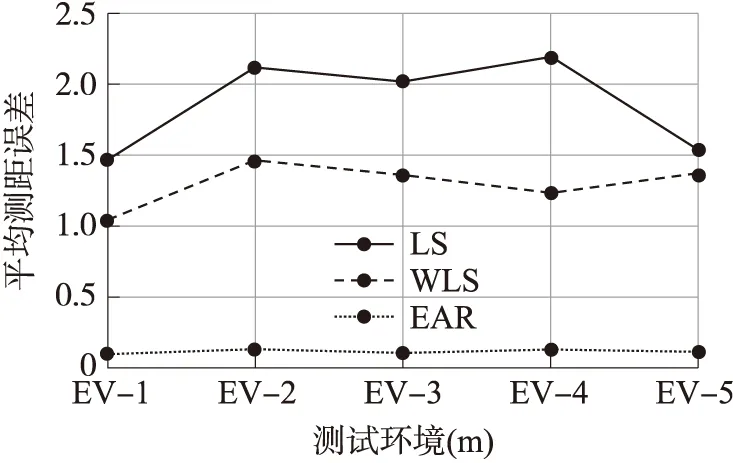
图4 平均测距误差Fig.4 Mean distance error

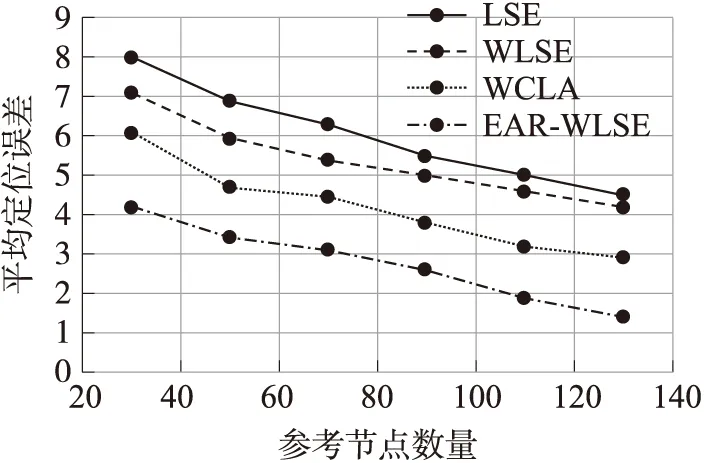
图5 平均定位误差Fig.5 Mean positioning error

4.2 动态环境自适应定位算法(DEAP)验证

在动态自适应定位算法(DEAP)的验证中,选取了WLSE、EAR-WLSE作对比. 为了模拟环境因素导致的无线电传播参数变化对定位精度的影响,定位测试区域为120 m×160 m. 设定目标的初始位置在[0 m,0 m],将定位区域划分为8个子域:A1～A8,每个子域均有不同的无线电传播特性,如图6所示. 设定所有参考节点的发射能量A均为-33 dBm,信号上叠加-4 dB噪声功率. 对于无线传播模型的N系数,假定在实际定位环境中,邻近定位区域有相似的传播特性,设定在A1～A8区域,N系数在2.0～4.0之间连续变化,邻域间差值为0.429. 为了验证参考节点密度对定位结果的影响,参考节点数量在1～100之间,均匀分布于定位区域. 为了研究目标动态特性对定位精度影响,令机动目标在0～80 s进行变加速曲线运动,初始速度为[0.2 m/s,1.2 m/s];在80～120 s做匀加速直线运动,加速度为[0.01 m/s2,0.01 m/s2];在 120～180 s做匀速直线运动. 采样间隔为1 s. WLSE各节点始终使用固定的N和A参数(与起始区域A相同),EAR-WLSE和DEAP使用自适应参数,在DEAP算法仿真时设定的位置量测噪声方差为15 m. 本文对各模型的计算误差统一采用均方根误差进行衡量[23]:

(6)

式中,N为Monte Carlo仿真次数,取100,x(k)和分别为k时刻目标状态的真实值和第i次滤波估计值. 在定位的起始区域A1,3种定位模型的对应的经验传播特性曲线系数都相同,且与真实环境传播规律保持一致. 实际运动轨迹和算法轨迹如图6所示. 图7显示了在一定参考节点数量下的平均定位误差-时间特性(AVG_ERR-T),在A1区域(0～50 s),因WLSE 中环境参数标定与实际相同,WLSE和EAR-WLSE定位误差相差不大,在A2及之后区域(50～180S)两者的相对误差逐渐变大,说明EAR-WLSE算法在变化的无线电传播环境下可自适应并显著提高定位精度. EAR-WLSE引入CS-EKF滤波方法得到的动态自适应定位算法DEAP,利用机动目标当前运动状态和定位观测信息进行最优估计,进一步降低了过程噪声,显著提高了定位精度. 图8的平均定位误差-参考节点数量特性曲线(AVG_ERR-N)显示参考节点数量与定位精度的关系. 上述算法精度都随着参考节点数量的增加而提高,DEAP算法精度最高.

节点数在0～50之内增加时,定位精度的提高比较显著. 在节点密度为6.25×10-3/m2时,DEAP比 EAR-WLSE 平均定位精度提高了48.75%,比WLSE提高了69.16%. 最大定位误差,DEAP比EAR-WLSE降低了39.58%,比WLSE降低了63.09%,如图9所示. 在AVG_ERR-T曲线可以看到,引入CS-EKF方法后,在25个参考节点数量下即可实现1M的定位精度,此时的节点的密度约为1.6×10-3/m2,可实现在稀疏节点密度下的精确定位,采用DEAP算法可大幅减少对参考节点数量的需求.

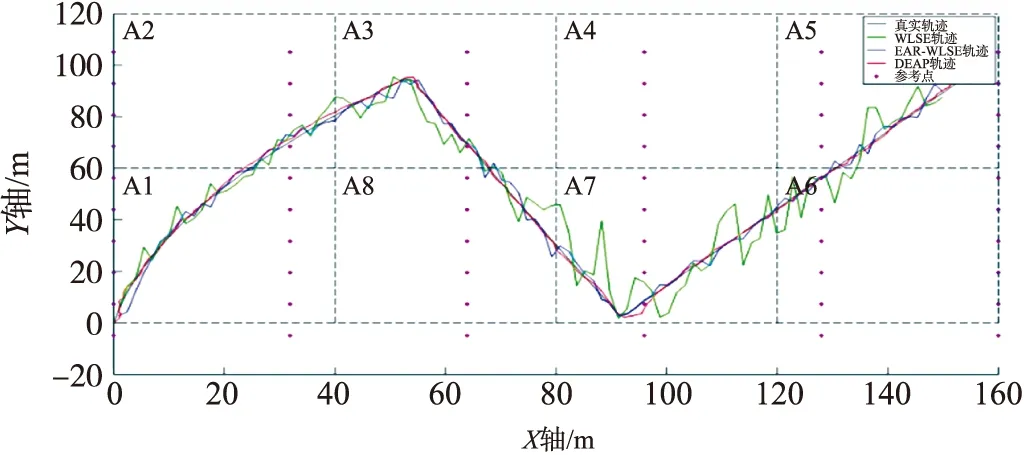
图6 目标定位轨迹Fig.6 Target location trajectory

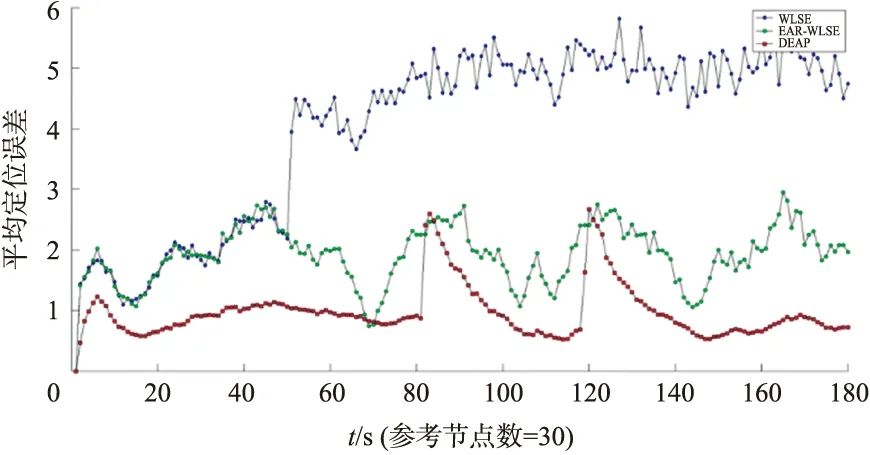
图7 AVG_ERR-T特性曲线Fig.7 AVG_ERR-T Curves

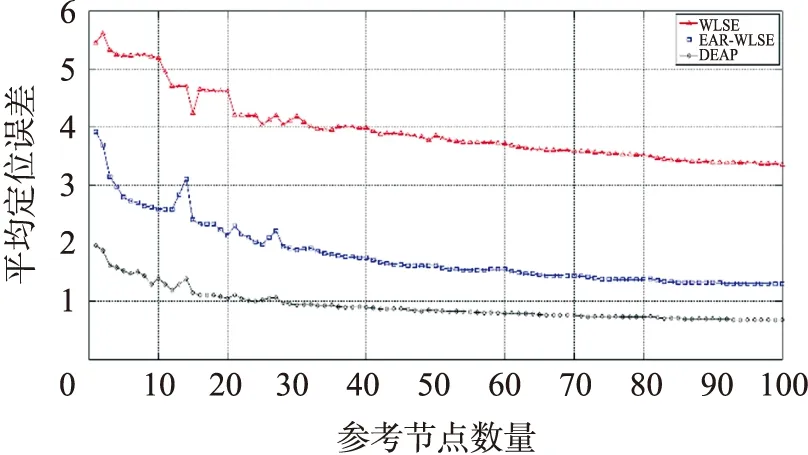
图8 平均定位误差曲线(AVG_ERR-N)Fig.8 Mean positioning error curves compare

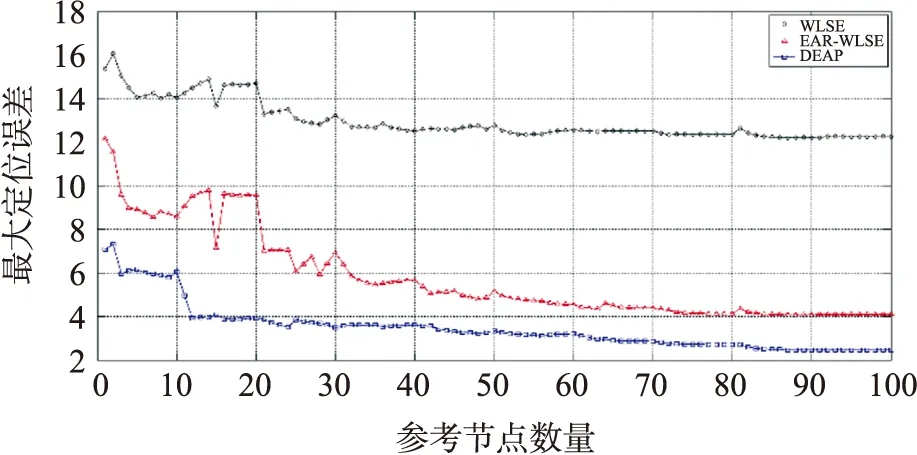
图9 最大定位误差曲线(MAX _ERR-N)Fig.9 Maximum positioning error curve

通过以上实验数据可以看到,DEAP算法具有最高的定位精度,EAR-WLSE次之,接下来是WCLA、WLSE和LSE. 由于无线电测距模型中距离误差的异方差特性,WLSE算法引入了权值矩阵对误差进行修正,得到了近似无偏估计,使其算法精度要优于无修正权值的LSE算法. 现实复杂定位环境中因温湿度、多径传输等因素会无线电传播系数出现局域性变化. 不同于本文提出的自适应定位算法EAR-WLSE算法,LSE、WLSE和WCLA等算法均采用固定的无线电传播系数,因而在传播系数变化的实际定位环境中会出现模型拟合误差,导致相对较大的定位误差. EAR-WLSE算法根据实际环境无线电传播特性辨识出精确的测距模型,根据距离解算出定位节点坐标,因而可自适应实际的无线电传播环境,实现高精度定位. DEAP算法是在EAR-WLSE算法基础上引入基于当前运动模型的扩展卡尔曼滤波方法而得. DEAP算法可有效抑制信号漂移产生的动态噪声,能进一步降低定位误差.

5 结论

为了解决复杂不确定性定位环境下基于RSSI定位算法存在的测距误差导致的定位精度问题,本文研究了在多径反射、非视距传输、温湿度变化等不确定情况下信号的传播特性. 在此基础上采用极大似然估计对实际传输特性进行极大似然拟合得到环境自适应测距方法-EAR,作为本文定位算法中的基础测距方法. 分析了信道噪声与距离衰减的关系,求解出近似无偏的距离权值,引入到加权极大似然估计算法后得到了静态自适应极大似然估计算法EAR-WLSE,大幅提高了静态定位精度. 针对EAR-WLSE算法求解目标动态过程中出现的漂移误差和动态噪声导致的定位误差问题,根据目标的运动特性,引入了 CS-EKF 滤波算法得到了动态自适应定位算法DEAP,进一步提高了动态定位精度. 综合实地测试及计算机仿真的结果表明,本文算法能自适应室内外复杂、不确定性定位环境,并可在稀疏节点密度下达到较高的定位精度,有效降低了对WSN基础设施的需求. 定位精度相比于WLSE算法,提高了69.16%,比WCLA提高了52%. 该方法适于一般性应用环境,为基于无线传感网络的节点定位提供了一种新的可选方案,具备普遍应用意义.