水下穿越管道悬空段受力特性的试验研究
2021-03-29杨庆华张宇倩王子聪
杨庆华,张宇倩,杨 乾,王子聪
(西南交通大学土木工程学院,四川成都610031)
作为国家能源的“命脉”,中国油气长输管道总里程累计已达到13.6×104km[1],在穿越河流、沟谷等水域[2]时,水下穿越管道通常被敷设在具有一定设计埋深的河床下,但由于河床演变、暴雨洪水及人工采砂等因素,极易造成管道裸露、悬空,形成跨度逐渐增大的悬空段,缺少河床保护的悬空管道部分或完全暴露于高速水流中,其受力性能受到严重影响,使得管道更易发生变形、屈曲、共振[3]乃至断裂等一系列破坏,造成巨大的经济损失及环境污染。根据中国近10年水下穿越管道事故统计[4],超过8成管道事故均来自管道悬空后发生的断裂破坏,因此,研究被水流冲出的穿越管道悬空段的受力特性对管道的运营、防护及科学管理具有重要意义。
国内外许多学者针对穿越管道进行了一系列研究,并在管道冲刷深度、局部冲刷扩展等方面取得较为丰富的成果,管道受力方面研究亟待完善。Brocchini[5]、Dogan[6]等针对波浪作用下海底管道的最大冲刷深度模型进行了完善。杨乾[7-8]等对水下穿越管道冲刷机理及悬空管道冲刷扩展规律进行了一系列研究,为研究管道受力奠定了基础。在管道受力方面,Magda[9-11]、Kumar[12]等分别对比分析了沙质、黏性土体中海底管道的受力情况,Sudhan等[13]通过试验完善了埋深、相对波高及散射参数对全埋海底管道受力的影响。雍崎卫[14]、任兴月[15]等最初利用理论分析方法探究了水下穿越管道的受力特性,为管道的设计埋深提供了一定的指导意义。李广雪[16]、李景阳[17]等通过引入物理试验将粉土海床中管道受力与地形变化情况相结合,探讨了不同冲刷阶段管道所受波浪力的情况。程永舟等[18]研究了斜坡角度、相对波高等参数对斜坡沙床上海底管道表面压力及总波浪力的影响,区分了管道局部及整体受力的差别。Xu等[19]讨论了黄河三角洲下海底管道受力与海床液化间的相关关系。在仿真模拟方面,张芝永[20]、姚熊亮[21]、张桦[22]、常留红[23]等基于多种流体力学软件对波流状态下海底管道周围流场、受力特性以及冲刷规律进行了一定研究,得到了管道受力状态与流场变化密切相关的结论。
综上所述,现阶段国内外有关管道受力的研究主要集中在海底管道,与内陆河流域中水下穿越管道不同,海洋流域流场复杂多变,管道受波浪、潮汐等因素共同影响,管道周围流场差异大,二者受力情况也大不相同。此外在有关管道受力的研究中,大多数学者考虑的变量因素较为单一,且均是在水流方向与管道垂直的条件下进行的,未考虑到管道与水流的夹角对管道受力的影响。基于此,作者通过开展缩尺物理模型试验,对多种参数下穿越管道悬空段所受的水流作用力进行试验研究,探究管径管道自身因素及流速、管道与水流夹角不同水动力因素对水下穿越管道悬空段作用力的影响规律。
1 试验模型设计
1.1 试验比尺
研究水下穿越管道悬空段在均匀单向流下的水流作用力,重力和惯性力起主导作用,遵循重力相似原则。则应有:

式中:λv为速度比尺;λg为重力加速度比尺,此处取λg=1;λL为几何比尺。
试验采用正态水力模型,根据《石油天然气工业管道输送系统用钢管》[24]规范,常用输气管道的直径范围为219~3 620 mm,考虑试验场地条件,最终确定几何比尺λL=25,其余参数均应参照该比尺进行换算,且换算结果应在合理范围内,各参数经比尺换算后得到的数值见表1。

表1 试验参数相似比尺表Tab.1 Test parameter scaletable
1.2 试验装置
试验在西南交通大学市政工程流体力学实验室进行,试验用水槽为单向循环水槽,水槽规格:长×宽×高=9.1 m×0.4 m×0.7 m。为便于观测,水槽侧壁均由透明钢化玻璃制成,设置于水槽头部的梯形堰和稳流板可为试验系统提供稳定流量(流量可通过读取堰流水深h1利用梯形堰计算公式求得),水槽末端设置有尾门,便于控制试验水深h2。试验段设置在水槽中下游,试验水槽布置示意图见图1,管道立面布置实图见图2。试验时,通过改变管道长度及摆放位置来控制管道与水流的夹角α(后统称为管流夹角);通过改变管径d及管道下边缘至水槽表面的距离h来控制管道的间隙比e(e=h/d,d为管径,h为管道底部至水槽底部的距离)。

图1 试验水槽布置示意图Fig.1 Schematic diagram of the test water tank layout

图2 试验管道立面布置实图Fig.2 Actual layout of the test pipeline elevation
1.3 试验管道与测量装置
为了探究不同管径管道的受力特性,按照几何比尺λL=25,采用3种不同管径的有机玻璃管,外径分别为3、4、5 cm。在每根管道中间断面上沿圆周均匀开6个孔,间隔为60°,以便安装高精度点式压力传感器,并按照角度逆时针方向分别编号为D1、D3、D5、D7、D9、D11,试验时通过逆时针旋转管道30°测得旋转后管道D2、D4、D6、D8、D10、D12的点压力,详见图3。试验所测12个点压力数值正负取指向管道中心为正,背离管道中心为负。试验所用高精度点式压力传感器量程为0~20 kPa,测量精度为0.1%,取采样频率为50 Hz。

图3 压力传感器布置图Fig.3 Pressure sensor layout
1.4 试验工况和流程
由流体力学实验可知,当均匀流体绕过静止不动的圆柱形管道时,除了受到垂直方向上水流压力外,在管道后方一定距离处,会产生由水流分离出具有一定周期性的漩涡,从而对管道形成周期性上下交替的水流压力,管道在这种压力作用下易产生周期性振动。由于试验流速较小,管道自重较轻,仅考虑管道在均匀流作用下管壁所受水流作用力的情况,可忽略管道振动对管道受力的影响。
为详细研究水下穿越管道悬空段的受力情况,试验变更了多种参数,探讨了在流量一定的情况下,流速、管流夹角、管径及间隙比对管道受力特性的影响。本试验设置3大组,共76小组组别试验。试验水泵可供最大流量为19.49 L/s,故设计流量一定,通过改变水槽水深来控制断面平均流速。根据Lei等[25]的研究,当间隙比处于0.2~0.3时,管后涡旋脱落及管道受力将受到底部边界层的影响,而当间隙比大于1.0时,底部边界层对的受力影响可忽略不计,因此,本次试验间隙比设计为1.0和2.0。详细工况组次见表2,其中每一种流速、间隙比下均要进行4中水流角度试验。

表2 试验因素水平表Tab.2 Test factor level table
试验开始时,先将管道模型按照设计要求依次连接压力传感器,压力传感器序号与图3点布置序号一一对应。随后依据各工况将管道两端按照一定位置固定在水槽壁上(管道可旋转),并将压力传感器连接计算机。待管道布置完毕后,打开水泵,关闭尾门,缓慢调节阀门,待水刚刚淹没管道时,采集零点,将连接计算机的各点压力传感器进行校零处理,接着保持水位不变逆时针旋转管道30°,采集旋转后各点的零点并记录,便于后续数据处理。零点采集完毕后将管道旋转回初始位置,增大流量至设计流量,通过调节尾门大小来调节试验水深h2至设计水深使得流速达到最小断面平均流速0.2 m/s,待水位稳定后,采集数据,该组点压力值采集完毕后,将管道逆时针旋30°,采集旋转后各点压力值,该流速下12个点数据采集完毕后再缓慢调节尾门,减小水深,增大流速至其余设计流速,待水位稳定后采集各点数据,以此类推,直至所有工况下各点数据均被采集完毕,试验结束。
2 管道受力理论分析
穿越管道悬空段在水下的受力主要由两部分组成,分别是静力荷载和水力荷载,静力荷载多与管道自身属性有关,重点探究不同工况下管道所受水力荷载的变化规律。
2.1 静力荷载
根据《石油地面工程设计手册》[26],穿越管道悬空段所受静力荷载主要由管道自重、管道浮力、管内石油(天然气)自重、管内操作压力、支座约束力以及土管耦合所产生的摩擦力等所组成,如图4所示。本试验管道模型为亚克力管,故忽略管道内压等静力荷载。

图4 管道静力荷载示意图Fig.4 Schematic diagram of pipe static load
2.2 水力荷载
水流流经悬空管道时,会产生圆柱绕流现象,如图5所示。当来流以一定流速作用于管道时,管道迎水面中部4点处压强最大,流速最小,水流在高压强的作用下从3、5点分道沿管道上下两侧壁面流动,形成边界层,其厚度与雷诺数及流程有关。在水流从管道迎水面4点处流至管顶1、管底7点的过程中,随着液流积压,流速沿程增大,压强逐渐减小,到达1、7点时流速达到最大,压强减至最小,即在4~1段和4~7段液流处于加速减压阶段,此过程中边界层内压能转化为动能。当水流从管顶1和管底7点处流至管道背水面8~12段时,由于圆管柱面的弯曲,液流发生扩散,流速逐渐减小,压强沿程增大,在9、11点处流速减小至0,压强增至最大,边界层内动能转化为压能,此时无动能的流体在尾部强压强作用下脱离圆管表面形成大小不一周期性交替脱离的涡旋,产生圆柱绕流现象。
综上所述,水流流经管道时,其流速及压强沿管道圆周发生变化,在理想状态下,管道迎水面中部压强最大,流速最小,管顶和管底流速最大,压强最小。将垂直于流速方向管道所受的水流力合力称为上升力Fy,将管道沿水流方向的合力称为水平拖曳力Fx。
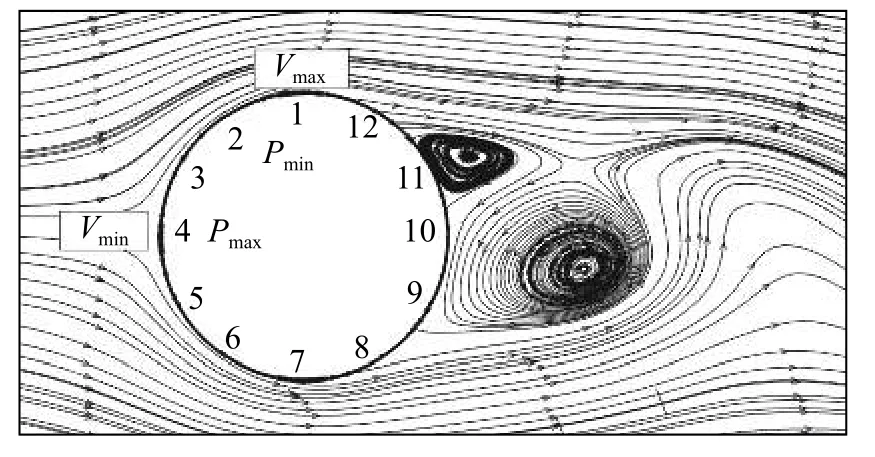
图5 圆柱绕流示意图Fig.5 Schematic diagram of flow around a cylinder
3 试验结果分析
3.1 管道表面点压力结果分析
由于来流流速不稳定,各点压力传感器所监测到的数据均为脉动值,而并非恒定值,其波动频率、幅度大小随工况的不同而改变。通常情况下,对于恒定流条件下管道各点所受压强,可采用时均压强来表示,即选取一段时间内的平均值作为监测值进行分析处理。基于此,取60 s内管道各点压强时均值进行分析。
数据处理完毕后,将各典型工况下点压强均值按照一定比例用曲线绘制成单位长度管道表面压强包络图,见图6~8。
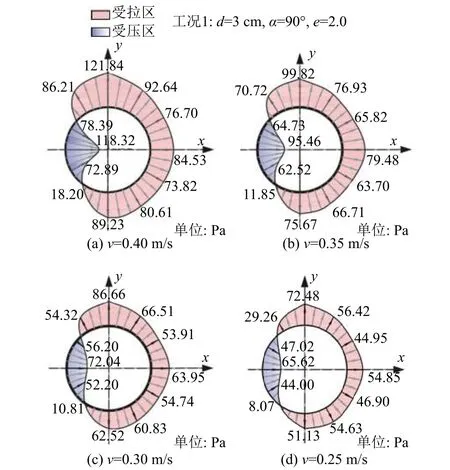
图6 不同流速下管道表面点压强包络图Fig.6 Pipeline point pressure at different flow rates

图7 不同管流夹角下管道表面点压强包络图Fig.7 Pipeline point pressure under different pipe flow angles

图8 不同管径、间隙比下管道表面点压强包络图Fig.8 Pipeline point pressure under different pipe diametersand gap ratios
不难发现,管道整体受力关于x轴趋于对称,除管道迎水面D3、D4、D5点处受力为压力外,其余各点均受拉力,管道整体所受合力方向为斜向右上。管道迎水面D3、D5点与背水面D9、D11点受力大小相近,方向相反,迎水面中点D4压力值最大;管顶D1处拉力值约为管底D7处拉力的1.05~1.25倍。将管道受力由压力转变为拉力的拐点称为分离点,并将管线受压区域称为受压面,受拉区域称为受拉面。从图中可以看出,管道分离点均位于圆管迎水面,且关于x轴趋于对称,受压面面积远远小于受拉面面积。
对比不同工况下单位长度管线表面压强包络图,分析图6可知,管道表面各点压力值均随流速的增大而增大,管道上下压力分离点的位置随流速的减小而有后移的趋势,即流速越小,管道受压面越平滑、范围越大,管道受拉面积减小。在不同管流夹角作用下,管道各点压力值均随管流夹角的减小而降低,如图7工况2所示。在管流夹角为45°、60°时其各点压力值较为接近,在夹角为30°时其值达到最小,且管流夹角越小,包络图越“瘦椭”,分离点位置亦随角度的减小而后移。这是因为当流速与管道不垂直时,流速可分解为沿管道轴线方向的流速和垂直于管道轴线方向的流速,轴向流速分量的存在导致到达管道迎水面的液流流速减小,从而使得管道表面各点压力降低,因此适当的管流夹角有助于减轻管道所受水力荷载。除此之外,综合分析图8(a)~(d),结合图6(b)可得,管道各点压力与管径呈正相关,与间隙比呈负相关,管道上下分离点位置随管径的增大而前移,随间隙比的增大而后移。产生这种现象的原因在于,随着管径的增大,管道受力面积增大,管道整体受力提升。到达管道迎水面的流速随间隙比的增大而降低,从而使得管道各点压力减小。
3.2 管道合力受力分析
根据管道表面点压强包络图(图6~8),图(图6~8)中各点压强与管道围成的面积即为单位长度管道所受的合力,将力分解到x轴、y轴方向,即可求得垂直于管道流速方向的上升力Fy和沿流速方向的水平拖曳力Fx。
3.2.1管道水平拖曳力变化规律
图9给出了不同流速、管流夹角、管径、间隙比下单位长度管道所受的水平拖曳力Fx。从图9中可以看出,单位长度管道所受水平拖曳力在1.5~13.5 N范围内变化,且受力大小随参数的变化呈现出不同的变化规律。从图9(a)中对比同一色系圆柱值可以得出,在管径、间隙比、管流夹角一定时,单位长度管道所受水平拖曳力随流速的增大而增大,且流速越大,其变化越为剧烈,在流速为0.40 m/s时最为明显。对比同一流速下不同管流夹角的柱体值可知,在流速一定时,随着管流夹角的增大,管道所受水平拖曳力亦有明显升高,且其受力大小在30°~60°间变化显著,在60°后变化较为微弱,这是因为在倾斜水流的作用下,管流夹角越小,流速沿管道轴线方向的分量越多,垂直于管轴的分量减小,导致管道受力越小,其变化越为明显。对比分析图9(b)可得,在流速、管流夹角一定时,管道所受水平拖曳力随管径、间隙比的变化较为显著,其大小与管径呈正相关,与间隙比呈负相关,且管径越大,其变化幅度越为剧烈。管道间隙比越大,管道前后的流速差越小,导致管道所受水平拖曳力越小。

图9 不同工况下单位长度管道所受水平拖曳力FxFig.9 Horizontal thrust force Fx of the unit length pipeline under different working conditions
3.2.2管道上升力变化规律
同管道所受水平拖曳力,不同工况下单位长度管道所受的上升力Fy见图10。单位长度管道所受上升力远小于管道所受水平拖曳力,其值约为管道水平拖曳力的1/10~1/20,大小介于0.1~1.6 N之间。管道所受上升力与水平拖曳力有相似的变化规律,但其变化幅度及规律性远不如水平拖曳力。与管道水平拖曳力类似,单位长度管道所受上升力与流速、管流夹角、管径呈正相关,与间隙比呈负相关。
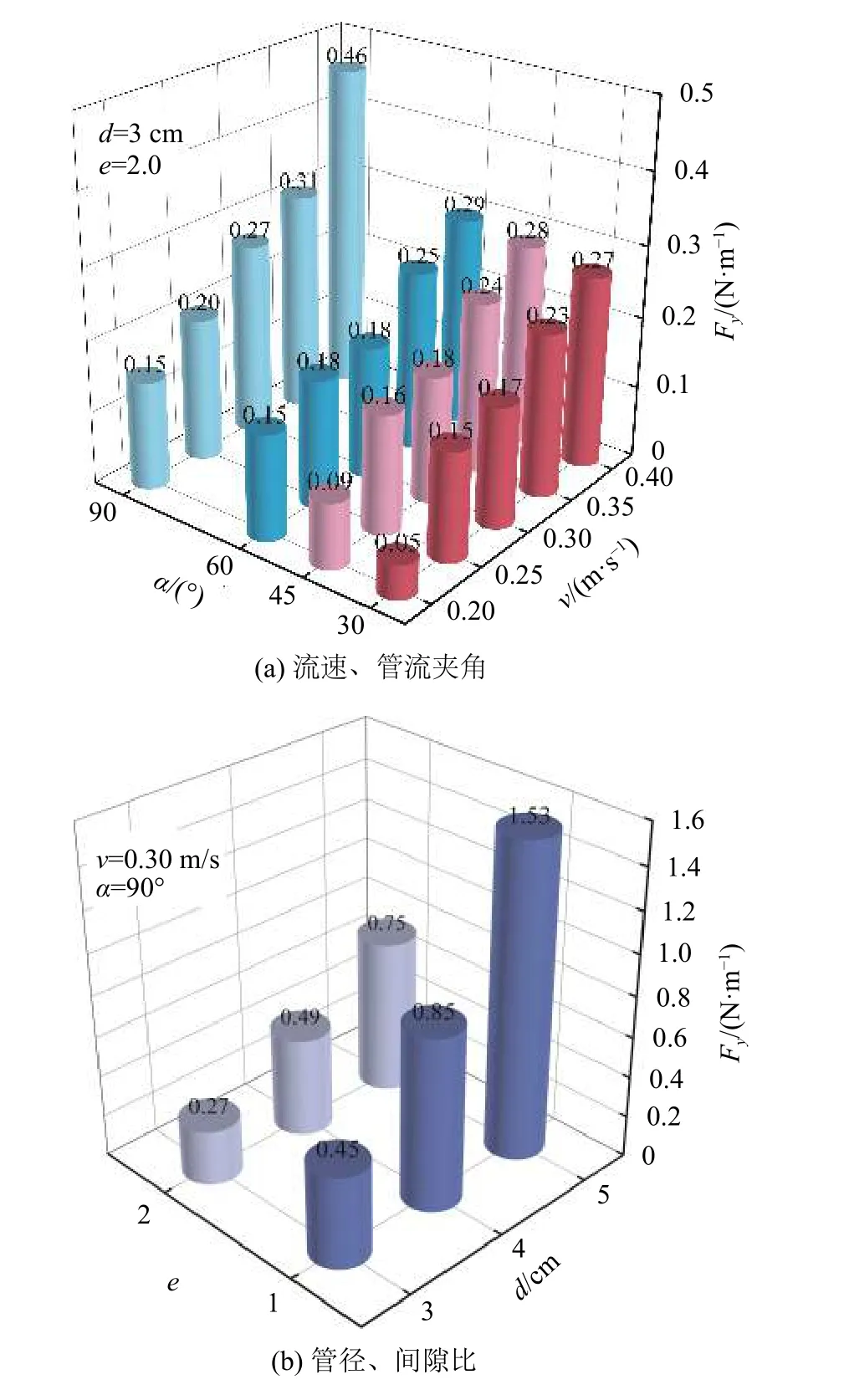
图10 不同工况下单位长度管道所受上升力FyFig.10 Rising force Fy per unit length of pipeline under different working conditions
3.3 管道受力经验公式拟合与验证
通过第2节研究,穿越管道悬空段在水流作用下会产生圆柱绕流现象,其所受水力荷载是管道与水流综合作用的结果。因此穿越管道悬空段所受水力荷载与管道自身因素及水动力条件密切相关。影响管道受力的管道自身因素有:管径d、间隙比e、管道长度l、管道密度ρt等;水动力参数有:流速v、管流夹角α、水流密度ρw、重力加速度g等。用F表示穿越管道悬空段所受水力荷载,则管道受力F的函数表达式为:
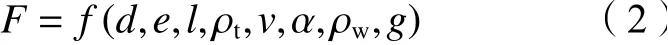
为研究单位长度管道的受力情况,不考虑管道长度l,此外,管道密度ρt、g为常数,不作为变量考虑。将管道受力分解为沿水流方向的水平拖曳力Fx和上升力Fy,则单位长度管道所受水平拖曳力Fx和上升力Fy均可用如下函数式表示:

根据量纲分析法,参考《石油地面工程设计手册》[26]水力荷载计算公式,管道所受水平拖曳力及上升力是关于管径d及流速v的指数函数,故单位长度管道所受水平拖曳力Fx和上升力Fy可表示为:
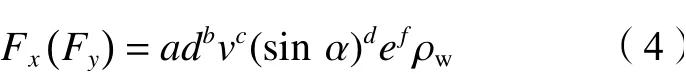
式中,a、b、c、d、f为待求未知参数。
运用多元线性回归模型,结合本文受力试验结果,对单位长度管道受力关系式进行拟合,求解式(3)中未知参数,得到单位长度管道水平拖曳力Fx及上升力Fy的最终表达式如下:

式(5)~(6)中:Fx、Fy为单位长度管道所受的力,N/m;d为管径,m;v为水流流速,m/s;α为管流夹角,(°);e为管道间隙比(e= h/d);ρw为来流水的密度,kg/m3。
为验证经验公式(5)、(6)的准确性和普适性,将试验结果与经验公式计算结果进行对比,见图11,从图11中可以看出,二者计算结果基本吻合,由此证明了上述公式对求解管道受力的准确性与普适性。
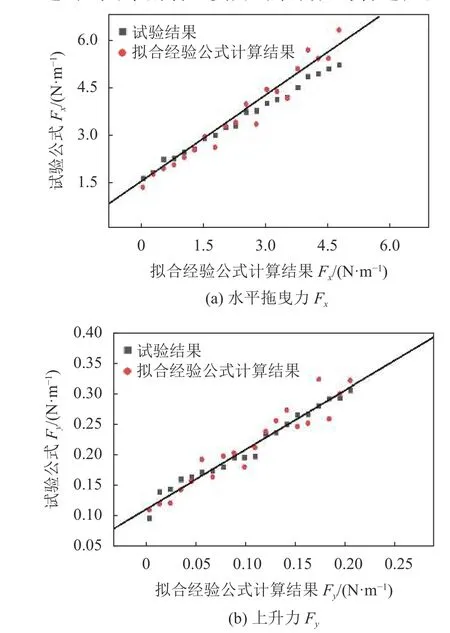
图11 管道受力试验结果与拟合经验公式计算结果对比Fig.11 Comparison of pipeline stress test results and calculation resultsof fitting empirical formula
3.4 工程计算实例
本文取成都地区某天然气穿越管道工程[27]为计算案例进行安全评估。该穿越管道位于成都市金堂县附近,穿越方式为挖沟法沉管穿越。穿越河段的水平直管段总长度为42.33 m,河床水平段管道最低埋深为3.87 m,穿越河段全长16 km,水域面积1.65 km2,平均比降0.15%。多年平均流量51.8 m3/s。枯洪水位悬殊,流量变幅大。该管道于2016年7月的一次暴雨中被冲断,冲断前最大悬空长度为7 m,穿越管道详细信息见表3,悬空管道距河床底距离为0.154 7 m,水流流速为3 m/s,不考虑管内油气自重及管道内压。

表3 水下穿越管道信息表Tab.3 Information sheet of underwater crossing pipeline

单位长度管道所受上升力为:

水下穿越管道虽然受到顺水流和垂直于水流的两个方向上的荷载作用,但是在强度安全评价时,把所有的荷载都看作是均布力作用,并且把两个方向的荷载加在一起,则该算例下水下穿越管道所受均布力之和为:

跨中截面的弯曲正应力为:
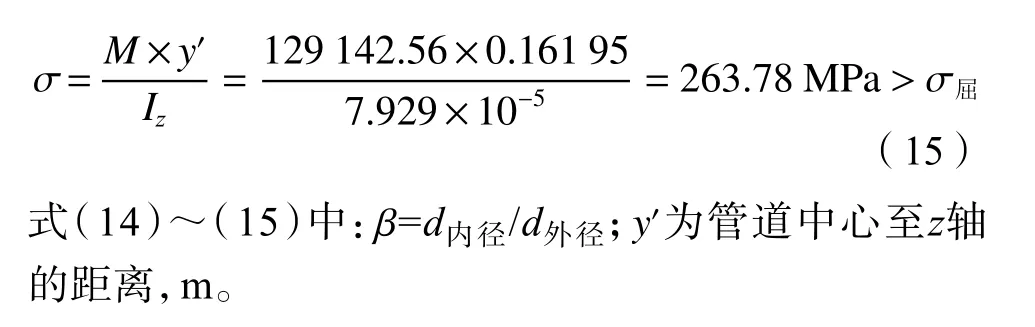
此时管道发生断裂破坏,与实际工程情况相吻合,进一步验证了式(5)、(6)的可靠性。
4 结 论
通过开展物理模型试验,研究了水下穿越管道悬空段的受力特性,分析了流速、管流夹角水动力参数及管径、间隙比管道自身因素对管道所受水流作用力的影响,得到以下几点结论:
1)除管道迎水面部分点受压力外,其余各点均受拉力,管道迎水面中点压力值最大,管顶拉力值约为管底的1.05~1.25倍。在流量一定时,管道表面各点压力值与流速、管流夹角、管径呈正相关,与间隙比呈负相关;分离点位置随流速、管流夹角、管径的增大而前移,随间隙比的增大而后移。
2)通过求解管道压力包络图面积即可求得单位长度管道所受合力。单位长度管道所受水平拖曳力Fx随流速的增大而增大,在斜向水流作用时,其受力有明显减小,管道斜置有利于其在水下的受力。此外,管径越大、间隙比越小,管道所受水平拖曳力也越大。
3)单位长度管道所受上升力Fy远小于管道水平拖曳力Fx,其值约为上升力的1/10~1/20。其大小随各参数的变化规律与管道水平拖曳力相同。
4)运用量纲分析法,结合多元线性回归模型,对单位管道受力公式进行推导与拟合,得到单位长度管道所受水平拖曳力及上升力的公式,试验结果与拟合公式计算结果吻合度较高。通过引入工程实例对该公式进行验证,进一步证明了该公式在实际工程应用中的普适性。
