超高性能轻质混凝土的循环拉伸力学性能

王俊颜，刘菲凡，郭君渊

(先进土木工程材料教育部重点实验室(同济大学)，上海 201804)

超高性能轻质混凝土(ultra-high performance lightweight concrete，UHPLC)[1-2]是利用超高性能混凝土(UHPC)的低水胶比、纤维增强、无粗骨料等原理制备[3]，并添加轻质细骨料制备而成的新型结构材料，其轻质细骨料被低水胶比浆体充分包裹而具备高抗渗性能[4]，通过纤维增强可实现拉伸应变强化和多点分布微裂纹，从而具备优异的裂纹宽度控制能力[5-6]。极限拉伸应变大于2.0×10-3[7-8]的配筋UHPLC结构在正常使用极限状态设计时无需考虑最大裂纹宽度的影响，因此可以充分利用钢筋强度，从而实现充分的优化设计，有望在材料低密度化的基础上进一步制备更轻量化的预制结构，比如大尺寸外挂墙板、轻量化预制楼梯、预制梁、浮岛式平台等。由于UHPLC需要与钢筋在高应力状态下协同工作(譬如钢筋达到200 MPa时，应变约为1.0×10-3)[9]，所以需要对UHPLC与钢筋的协同受拉力学性能进行研究。目前关于配筋UHPC拉伸试验不多[10-11]，关于循环加载的更少。本文针对UHPLC在4种加载条件下(循环应变分别是2.0×10-4、5.0×10-4、1.0×10-3、1.5×10-3)的力学性能开展系统研究，并深入分析其残余应变、加载卸载刚度等力学性能参数随循环加载次数的影响，并分析其刚度退化机理和模型，目标是为轻量化的配筋UHPLC结构设计提供基础理论依据。

1 试验概况

1.1 试验原材料及配合比

本文中采用的UHPLC的设计密度为1 800 kg/m3，水胶比为0.23，纤维掺量为2.25%。配合比见表1，其中水泥采用江南-小野田水泥厂生产的P·Ⅱ 52.5 硅酸盐水泥，28 d抗压强度为60.1 MPa；硅灰采用埃肯公司生产的微硅粉，平均粒径为0.10～0.15 μm，比表面积为22 000 m2/kg，SiO2质量分数为94.48%；轻质填料用粒径范围在0.15～0.3 mm和0.3～1 mm的两种轻质材料进行复配，堆积密度为200 kg/m3；减水剂采用粉末状聚羧酸系高效减水剂，减水率为25%；引气剂为粉状的茶皂素基引气剂；纤维采用平直形镀铜钢纤维，相关性能参数见表2。

表1 UHPLC配合比Tab.1 Mix proportion of UHPLC kg/m3

表2 纤维的力学性能Tab.2 Mechanical properties of fibre

1.2 试件制备及养护方法

UHPLC采用如下搅拌程序：启动搅拌机→投入粉料(含外加剂)→干拌3 min→加水→搅拌3～5 min(物料达到流态)→投入纤维→继续搅拌2 min以上→出料成型试件。将搅拌物浇筑在钢模中，经抹面后加盖塑料膜，以防止水分的快速散失，室温下静置24 h后拆模。脱模后的试件进行标准养护，温度为20±3 ℃，相对湿度90%以上。

试件分为5组，均为相同配合比，包括1组单调拉伸加载试件以及4组不同等幅变形循环拉伸加载试件(循环应变分别是2.0×10-4、5.0×10-4、1.0×10-3、1.5×10-3)。每组试件均包含3个狗骨头拉伸试件(图1)。同时根据GB/T 17671—1999成型40 mm×40 mm×160 mm的棱柱试件测试28 d强度，测试强度前用排水法测试试件的硬化密度。

图1 狗骨头拉伸试件(mm)Fig.1 Dog-bone-shaped tensile specimen (mm)

1.3 加载装置及试验方法

在10 t的电子伺服万能试验机上进行UHPLC的拉伸试验，试验机的试验力和变形的示值准确度均为±0.5%。本文为避免拉伸加载偏心，使用了一套专用夹具，见图2。

图2 拉伸试验装置Fig.2 Tensile test setup

狗骨头拉伸试件由上下夹具固定，中间纯拉段固定有两个矩形金属架，两者之间距离即为试件的测试标距L，本文定为150 mm。两个金属架用来安装精度为0.000 1 mm的两个线性可变位移计， 以测量轴向拉伸变形，并转化为试件的应变值ε(ε=(Δl1+Δl2)/2L×100%， Δl1和Δl2为两个位移计变形值)，最终与电脑采集的拉伸应力值形成拉伸应力-应变曲线。试验加载速度设置为0.3 mm/min(试验机横梁加载速度)。

UHPLC的单调拉伸加载在拉伸应力小于峰值应力的80%时结束试验。UHPLC循环拉伸试验的每次循环由预加载、正式加载和卸载三部分组成，试验全程采用等位移加载控制，预加载的速度为1 mm/min，正式加载及卸载的速度均为0.3 mm/min。当荷载超过0.5 kN时，试验进入正式加载阶段；当加载至目标拉伸应变时，试验进入卸载阶段；当荷载降至0.5 kN时，单次循环加载结束。

2 结果与分析

2.1 UHPLC的拉伸应力-应变曲线

UHPLC的40 mm×40 mm×160 mm棱柱试件抗压强度为63.1 MPa，硬化密度为1 789 kg/m3，相对传统UHPC的密度降低了28%。图3给出了3根UHPLC的拉伸应力-应变曲线，UHPLC的拉伸应力-应变曲线呈现出明显的3个阶段，即弹性段、应变强化段和应变软化段。UHPLC的弹性极限强度较低，约为3～4 MPa，随后迅速转入应变强化段(转折点不明显，大约在应变为1.6×10-4处发生转折)，极限拉伸应变约为2.4×10-3～2.8×10-3，极限抗拉强度约为6.9～7.8 MPa， 与弹性极限强度的比值范围是1.8～2。试验过程中发现，在应变强化阶段，UHPLC展示出很强的裂纹宽度控制能力，裂纹宽度不可见或小于0.05 mm。UHPLC展示出较低的弹性极限强度、较高的应变强化性能和裂纹控制能力，这是由于UHPLC采用了粒径比水泥粗并且强度较低的轻质填料，降低了UHPLC基体的断裂韧性，但纤维仍保持与UHPLC基体较高的黏结强度，从而实现不可见的多点分布微裂纹开展模式。这种特性可让UHPLC与普通钢筋(如HRB400)在钢筋屈服之前保持良好的协同受拉作用，以及配筋UHPLC结构优异的裂纹宽度控制能力。

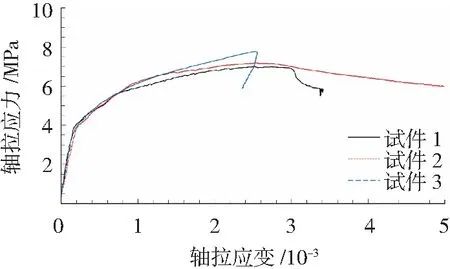
图3 UHPLC的拉伸应力-应变曲线Fig.3 Tensile stress-strain curves of UHPLC

2.2 循环拉伸加载条件下UHPLC的应力-应变曲线

4组拉伸试件的循环加载次数为8～11次不等，并且一般在第四次循环之后，加载卸载曲线会趋于稳定。为方便分析，本文取了8次循环曲线进行深入分析，见图4。

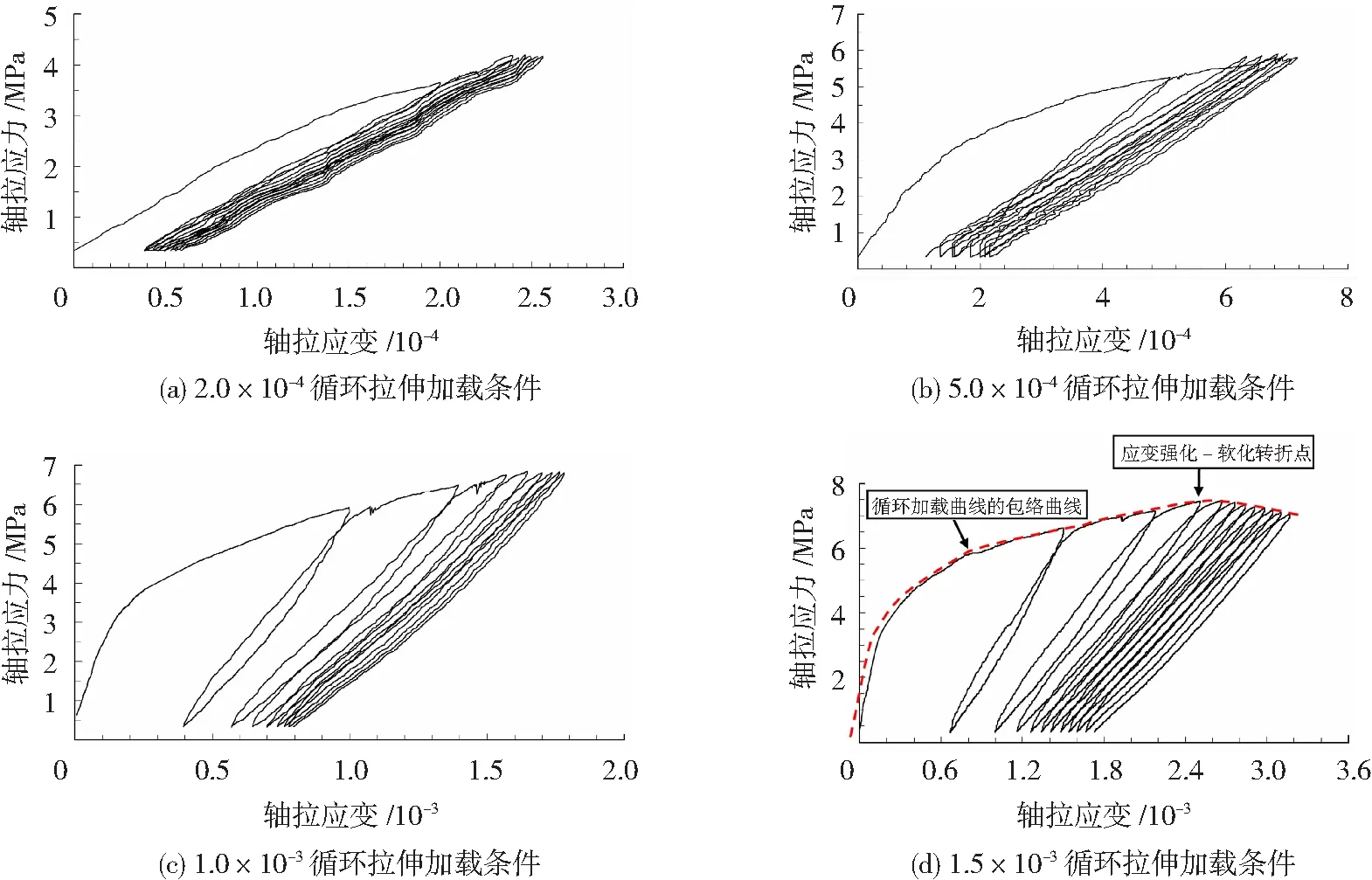
图4 不同循环加载条件下UHPLC的应力-应变曲线Fig.4 Stress-strain curves of UHPLC under different cyclic loading conditions

由图4可见：1)等幅加载变形越小，循环曲线越密集，残余应变也越小，反之，循环曲线越分散，残余应变也越大；2)4组循环加载曲线的外包络线与图3所示的全曲线基本吻合，特别是加载变形为1.5×10-3时，其循环曲线的包络线在应变为2.6×10-3处进入应变软化段，较明显地呈现出UHPLC拉伸曲线的3个阶段；3)由于在塑性段时UHPLC基体已经断裂，主要由纤维桥接贡献承载力，因此循环加载曲线的残余应变、加载刚度、卸载刚度均间接反映了桥接裂纹处纤维的黏结和脱黏状态。可以预见，对于小的等幅变形循环加载条件(如应变分别是2.0×10-4和5.0×10-4)，纤维脱黏长度较短，参与拉伸变形的有效长度较小，拉伸试件在单位变形条件下的纤维变形量高，所以纤维拉伸应力较高，表现出的拉伸试件刚度更高。对于大的等幅变形循环加载条件(如应变分别是1.0×10-3和1.5×10-3)，纤维脱黏长度增大，参与拉伸变形的有效长度较大，拉伸试件在单位变形条件下的纤维变形量低，因此纤维拉伸应力不高，表现出的拉伸试件刚度变低。

4种不同循环加载后的试件见图5，由图5可见，加载变形为1.5×10-3的试件进行11次循环后，由于累积应变大于UHPLC的极限应变，已经进入应变软化段，因此有可见裂纹。其余试件由于累积应变小于UHPLC的极限应变，处于应变强化段，无可见裂纹，试件保持完整。

图5 循环后的轴拉试件Fig.5 Tensile specimen after cyclic loading

2.3 循环拉伸加载条件下UHPLC的力学性能

循环拉伸加载条件下的UHPLC的力学性能参数定义见图6。参考文献[12-13]中曲线刚度的确定方法，本章在每次轴拉循环曲线的加载段和卸载段的0%～40%极限应力段分别拟合直线，其对应斜率即为加载刚度和卸载刚度。图6中El和Eu分别表示加载刚度和卸载刚度(括号里表示循环次数序号)。由于UHPLC进入应变强化段之后纤维发生了局部脱黏，部分变形无法在卸载后恢复，因此存在残余应变，并且残余应变会进行累积。本文定义的残余应变为每次循环的卸载曲线回到荷载初始值(0.5 kN，对应应力为0.33 MPa)的应变与加载曲线起始应变值的差值。

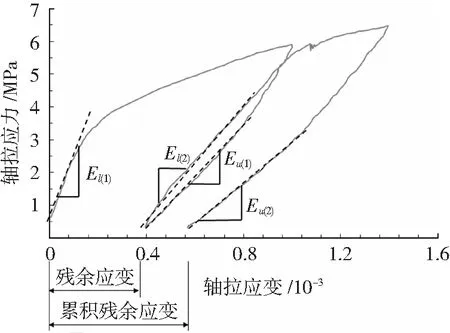
图6 循环拉伸加载下UHPLC的力学性能表征Fig.6 Characterization of mechanical properties of UHPLC under cyclic tensile loading

表3列出了不同循环拉伸加载条件下UHPLC的力学性能，并且在图7～10分别给出了残余应变、峰值应力、 加载刚度、 卸载刚度随循环次数的变化规律。

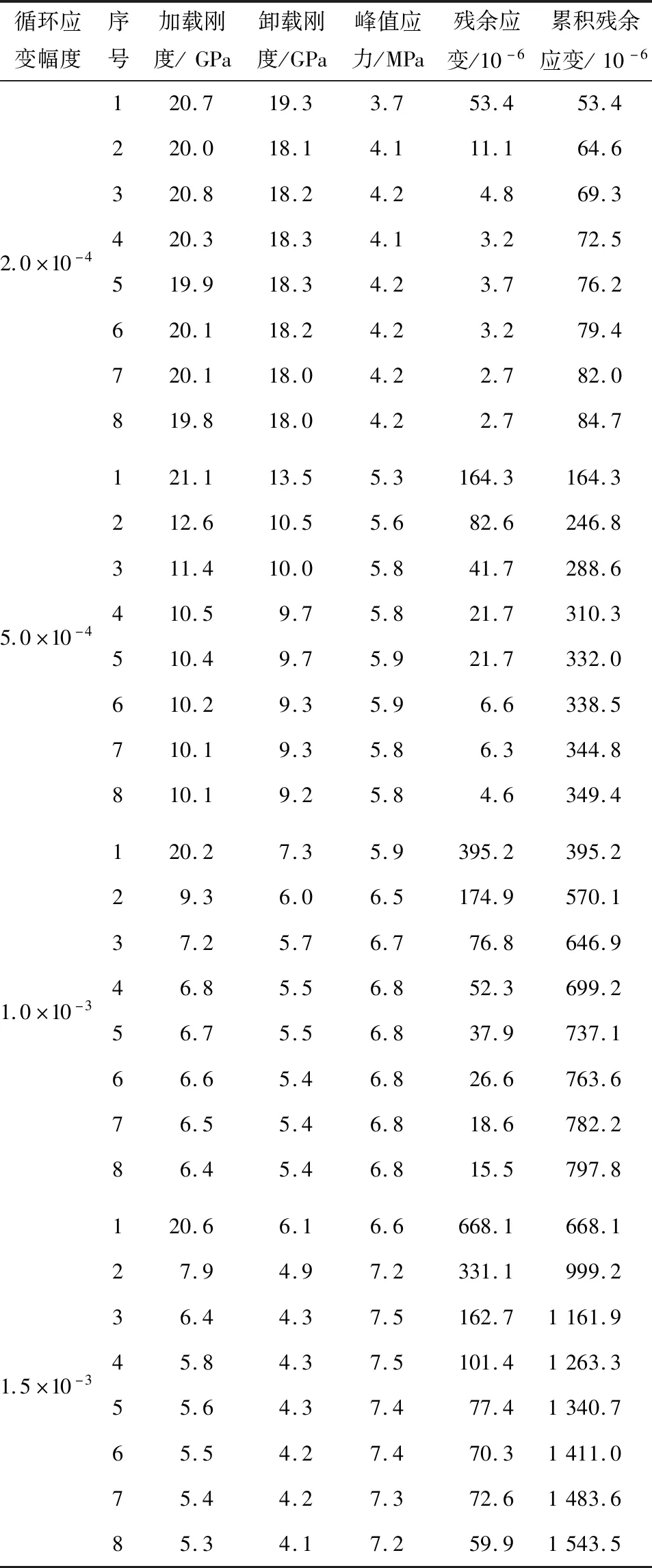
表3 不同循环拉伸加载条件下UHPLC的力学性能Tab.3 Mechanical properties of UHPLC under different cyclic tensile loading conditions

图7 轴拉循环荷载下UHPLC的残余应变随加载次数的变化Fig.7 Effect of the number of tensile cycles on residual strain of UHPLC

2.3.1 残余应变

由图7可见，不同循环拉伸加载条件下UHPLC的残余应变均在第三次循环之后趋于稳定。从微观角度看，这是由于UHPLC在循环拉伸加载条件下的损伤主要表现为基体的开裂、以及纤维与基体的逐步脱黏，因此宏观角度表现为卸载后所产生的不可恢复的残余变形(应变)。对于2.0×10-4、5.0×10-4和1.0×10-3这3种应变加载条件，随着循环次数增多，UHPLC不可恢复的残余变形逐渐降至零，说明此时纤维与基体的继续脱黏现象基本停止，循环加载主要是对已脱黏部分纤维的循环拉伸作用。对于1.5×10-3这种应变加载条件，从第四次循环开始，UHPLC已经进入应变软化段，此时某截面处的纤维已部分处于拔出状态，因此后续的残余应变仍比较高，第八次循环加载后的残余应变仍高达6.0×10-5。

2.3.2 峰值应力

由图8可见，4种循环加载条件下的UHPLC在前3次循环中的峰值应力均有小幅提高，但第四次循环之后，在1.5×10-3的应变加载条件下，UHPLC的峰值应力有所降低，而其他3种加载条件下的UHPLC的峰值应力则基本保持一致。这同样是由于在1.5×10-3的应变加载条件下，UHPLC第四次加载的累积应变已经达到2.6×10-3，UHPLC已进入应变软化段的原因。

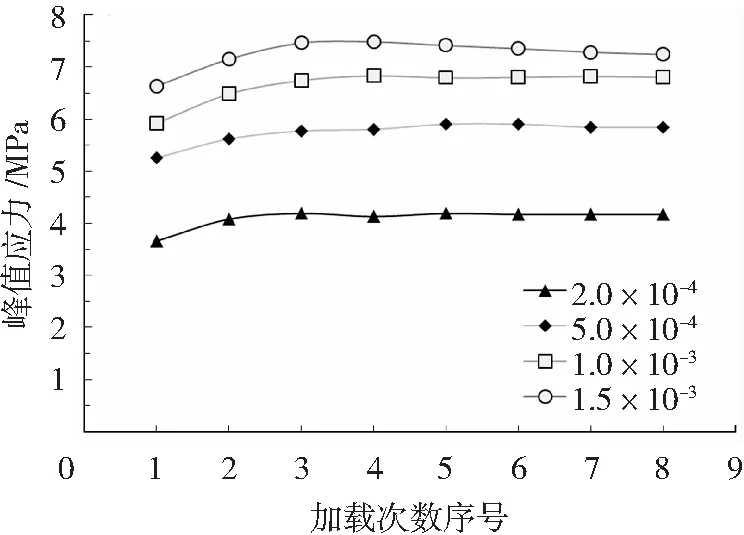
图8 轴拉循环荷载下UHPLC的峰值应力随加载次数的变化Fig.8 Effect of the number of tensile cycles on ultimate tensile stress of UHPLC

2.3.3 加载刚度和卸载刚度

由图9可见，在2.0×10-4的应变加载条件下，UHPLC的加载刚度变化幅度很小，这是由于其加载变形幅度较小，略大于弹性段和应变强化段的转折点(应变为1.6×10-4)。其余3种循环加载条件下UHPLC的加载刚度均有较大的衰减，并且循环加载变形幅度越大，衰减幅度越大。这是由于循环加载变形幅度的增大会导致UHPLC的纤维脱黏长度增大，即参与拉伸变形的有效长度变长，拉伸试件在单位变形条件下的应力水平更低，表现出的拉伸试件刚度变低。

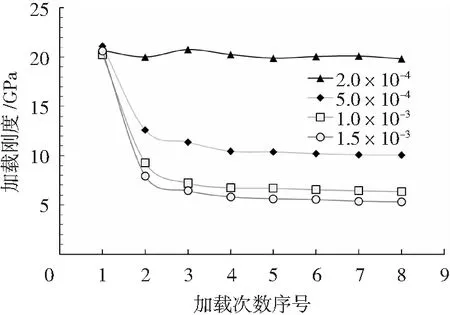
图9 轴拉循环荷载下UHPLC的加载刚度随加载次数的变化Fig.9 Effect of the number of tensile cycles on loading stiffness of UHPLC

由图10可见，UHPLC在不同循环加载条件下的第一次卸载刚度随加载变形幅度的增大而降低，这同样是因为循环加载变形幅度的增大导致UHPLC纤维脱黏长度增大的原因。综合图9、图10可见，UHPLC的加载刚度和卸载刚度在第三次加载-卸载后逐渐趋于稳定。结合图7可发现，UHPLC的加载刚度和卸载刚度随循环加载次数的变化趋势与残余应变的变化趋势基本一致。这说明UHPLC的加载、卸载刚度与材料的残余应变相关。

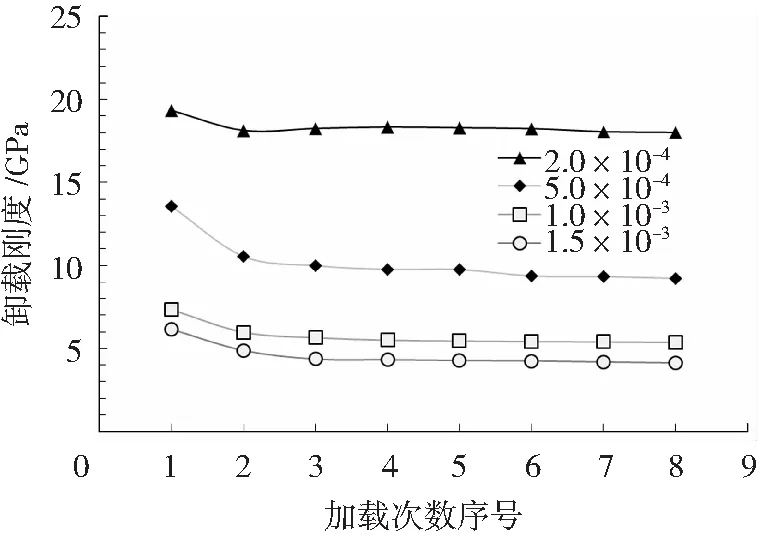
图10 轴拉循环荷载下UHPLC的卸载刚度随加载次数的变化Fig.10 Effect of the number of tensile cycles on unloading stiffness of UHPLC

3 循环拉伸加载条件下UHPLC的刚度退化机理

为进一步了解UHPLC在循环荷载下的加载刚度退化率与材料残余应变之间的关系，图11绘制了UHPLC的加载刚度退化率(El(n)/El(1))与前一次循环达到的累积残余应变的关系，退化率越低说明材料刚度退化现象越严重。由图可见，UHPLC的加载刚度退化率随累积残余应变的增加而降低， 其衰减规律符合式(1)的幂函数，拟合度为0.99。

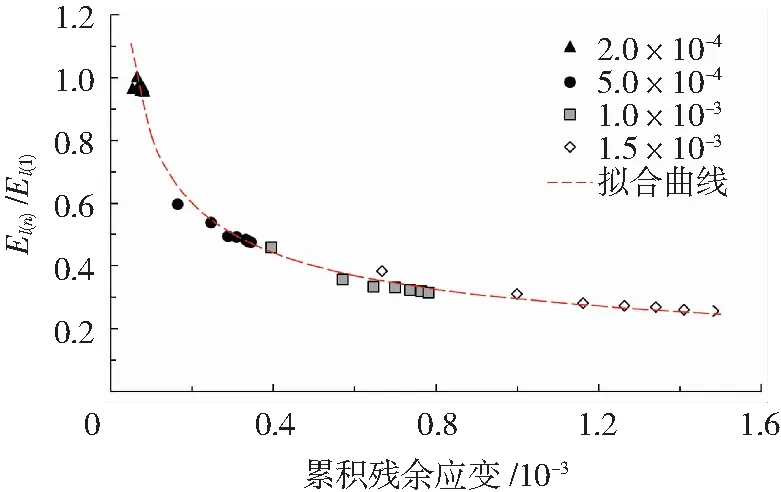
图11 累积残余应变与加载刚度退化率的关系Fig.11 Effect of cumulated residual strain on degradation rate of loading stiffness

y=6.223x-0.441

(1)

式中y为加载刚度的退化率(El(n)/El(1))，x为累积残余应变。

图12描述了应变强化段的纤维-基体相互作用示意图。由图12可见，UHPLC基体开裂后，开裂处的荷载由两端处于锚固状态的纤维承担。随着外荷载的增加，纤维受到的拉应力大于开裂处纤维-基体界面黏结强度，纤维逐渐脱黏，导致参与变形的纤维有效拉伸长度变大，即UHPLC的不可恢复变形增加，其宏观表现为累积残余应变的增加。纤维有效拉伸长度的提高，降低了拉伸试件在单位变形条件下的拉伸应力，表现出UHPLC刚度变低。综上所述，UHPLC在循环拉伸加载条件下的刚度本质上由纤维的有效拉伸长度决定，并且其纤维有效拉伸长度可由累积残余应变来表征。

4 结 论

1)UHPLC极限抗拉强度约为6.9～7.8 MPa，与弹性极限强度的比值范围是1.8～2，具有较强的应变强化特性。同时其极限拉伸应变约为2.4×10-3～2.8×10-3，在应变强化段的裂纹宽度不可见或小于0.05 mm，具有较强的变形能力和微裂纹宽度控制能力。

2)不同加载条件的UHPLC的循环拉伸应力-应变曲线的包络线与单调拉伸应力-应变全曲线具有较高的重合度。

3)循环加载曲线的残余应变、加载刚度、卸载刚度均间接反映了桥接裂纹处纤维的黏结和脱黏状态。残余应变越大，说明纤维的脱黏长度越长，会导致UHPLC的加载、卸载刚度降低。

4)对于2.0×10-4、5.0×10-4、1.0×10-3这3种应变加载条件，随着循环次数增多，UHPLC的纤维与基体的继续脱黏现象基本停止，循环加载主要是对已脱黏部分纤维的循环拉伸作用。对于1.5×10-3这种应变加载条件，从第四次循环开始，UHPLC已经进入应变软化段，此时其纤维已部分处于拔出状态，因此后续循环的残余应变仍比较高。

5)UHPLC在循环荷载下加载刚度的退化率与累积残余应变具有较高的相关性，两者关系符合幂函数关系，拟合度为0.99。UHPLC的循环拉伸加载刚度本质上由纤维脱黏部分参与受拉的有效长度决定，可由累积残余应变来表征。