约束混凝土受压应力-应变曲线统一方程
2021-03-29李柯璇郑文忠侯翀驰
李柯璇,郑文忠,侯翀驰,王 英
(1.结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090;2.土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090)
随着混凝土技术的发展,高强度及超高强度混凝土的应用成为发展趋势。但混凝土强度越高,脆性愈发明显,限制了其在工程中的推广应用。用箍筋约束混凝土是一种改善混凝土脆性的有效方式。随着约束混凝土柱中混凝土强度提高,所配置的箍筋强度也在不断增加。中国《混凝土结构设计规范》[1]推广HRB400、HRB500钢筋的使用,顺应高强度箍筋约束高强度及超高强度混凝土结构的发展趋势。
文献[2]对约束混凝土的应力-应变全曲线进行了研究,该模型的上升段和下降段分别取决于两个独立的试验参数,形式简洁。但研究的混凝土强度在28~40 MPa,对强度较高的混凝土的适应性还需验证[3]。试验仅考虑了矩形箍筋对约束混凝土应力-应变曲线的影响,没有考虑其他箍筋形式对约束混凝土承载能力和变形能力的影响。
文献[4-5]对箍筋屈服强度为300~340 MPa,体积配箍率为1%~2%,纵筋配筋率为1.6%~4.8%的约束普通强度混凝土圆柱受压应力-应变关系进行研究,提出了适用于多种箍筋形式的约束混凝土受压应力-应变关系上升段和下降段统一的方程。Mander模型考虑了箍筋形式、体积配箍率、箍筋间距、箍筋强度及纵筋的影响,但对高强及超高强混凝土的适应性还需进一步研究。
文献[6]提出了适用于高强混凝土的应力-应变模型,该模型考虑了混凝土强度等级、箍筋形式、体积配箍率、箍筋间距、箍筋屈服强度、截面尺寸等因素的影响。曲线下降段形式较简单,便于应用,但模型没有考虑纵筋配筋率对约束效果的影响。
文献[7]对箍筋条件屈服强度分别为411、716、1 120 MPa,混凝土强度等级C70~C80的约束混凝土圆柱进行了试验,给出了约束混凝土峰值应力、峰值应变及本构关系方程。研究过程发现当箍筋屈服强度高于700 MPa时,体积配箍率为1.3%~4.2%的约束混凝土达到峰值应力时箍筋未屈服。
文献[8]对非约束混凝土强度为120~160 MPa,体积配箍率为0.8%~2.1%的约束超高强混凝土圆柱进行轴压试验,提出了受压应力-应变关系的上升和下降分支模型,并且提出了一种残余应力计算方法。该模型对约束超高强混凝土准确性较高,但对普通混凝土及高强混凝土适应性还需验证。
已有的约束混凝土本构关系模型,大多是基于各自试验数据得到的,适用范围不同且有限。本文针对这一问题,收集大量试验数据统一处理,建立了混凝土强度为19~160 MPa,箍筋屈服强度为164~1 386 MPa,体积配箍率为0.15%~16.7%,纵筋配筋率为0%~5.87%的约束混凝土轴压试验数据库。在此基础上,提出了约束混凝土受压应力-应变曲线统一方程和峰值压应力、峰值压应变计算公式。经验证,该方程适用范围广,准确度较高,有较高的理论意义和工程使用价值。
1 约束混凝土本构关系数据库的建立
1.1 本文试验数据
本课题组已完成47个螺旋箍筋约束混凝土圆柱轴压试验[9],作为补充验证性数据,考察本文结论的准确性。测得试件轴压应力-应变曲线及约束混凝土峰值压应力和峰值压应变的值。试验结果见表1。
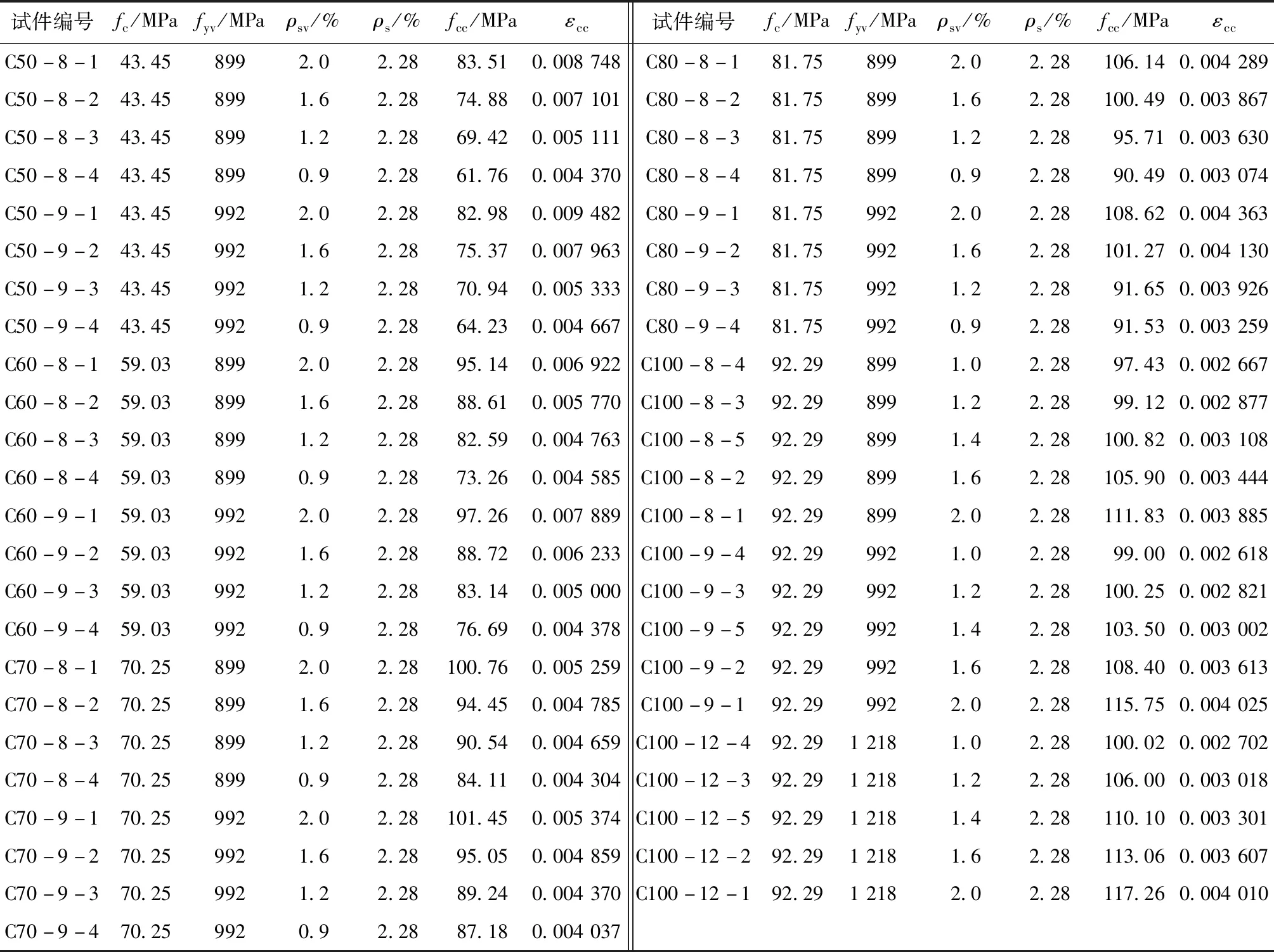
表1 本文试验结果Tab.1 Experimental results of this paper
1.2 数据库试验数据处理方法
为避免由于各文献中对数据处理方法不同带来的误差,对搜集的试验数据按下列方法进行统一处理。
1.2.1 混凝土保护层处理方法
本文在处理试验数据时,假定纵筋应变与混凝土应变相同[10],核心混凝土的承载力计算该公式为
F0(ε)=F(ε)-Acovfcov(ε)-Asfs(ε)
(1)
式中:F0(ε)为轴向应变为ε时试件核心混凝土的轴向力,F(ε)为轴向应变为ε时试件全截面的轴向力,Acov为混凝土保护层截面面积,As为纵筋总截面面积,fcov(ε)为轴向应变为ε时对应的保护层混凝土应力,fs(ε)为竖向应变为ε时的纵筋应力。
纵筋采用的本构模型在第1.2.3中详述。保护层混凝土本构模型采用过镇海模型[2]。图1是试件中保护层混凝土应力-应变关系示意。采用式(1)计算核心混凝土的承载力时,若轴向应变(εp)在混凝土极限压应变(εu)与剥落应变(εsp)之间时,见图1(a),假定保护层混凝土承担的荷载线性下降;若εp>εsp,见图1(b),则Acovfcov(ε)=0。计算时,按下列标准来判断混凝土保护层是否已剥落:fc<50 MPa,取εsp=0.003;50 MPa
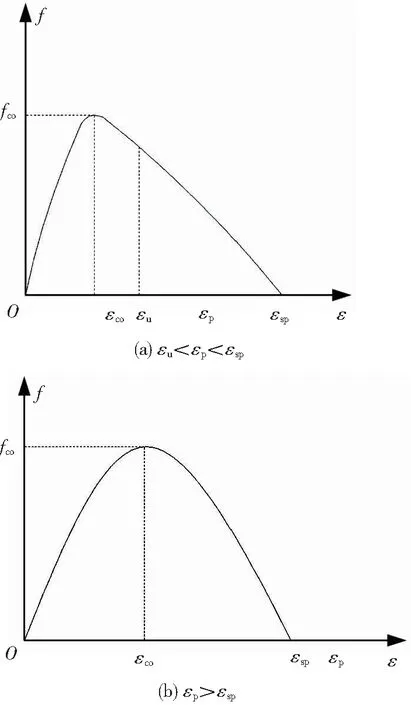
图1 试件保护层混凝土应力-应变关系示意Fig.1 Schematic diagram of the stress-strain relationship of the concrete protective layer of the specimen
1.2.2 箍筋应力的计算方法
箍筋约束混凝土轴压试验中,约束混凝土达到峰值压应力时,箍筋能否达到屈服强度是不可忽视的问题。对搜集的数据进行处理分析,采用本课题组已有研究成果[9],将体积配箍率作为判断箍筋在约束混凝土达到峰值压应力时是否屈服的依据。箍筋屈服时,体积配箍率上限值ρsv,max和箍筋屈服强度、非约束混凝土轴心抗压强度、箍筋和混凝土弹性模量存在关系,计算公式[9]为
(2)
当体积配箍率小于该限制,则假定箍筋达到屈服强度,否则认为箍筋无法达到屈服强度,此时箍筋应力水平计算公式[6]为
(3)
式中:Es为钢筋弹性模量;ρsv为体积配箍率;fco为非约束混凝土峰值压应力;fsy为箍筋屈服强度;k′与柱中配筋分布有关,系数k′由经验表达式(4)计算得到[6]。
(4)
式中:s为箍筋间距,sl为纵筋间距,bc为水平面箍筋净距,箍筋内沿间的距离。
1.2.3 纵筋应力处理方法
搜集到的约束混凝土峰值压应力试验数据,有一部分考虑了部分纵筋应力影响。本文处理时,假定纵筋与核心混凝土无相对滑移,核心混凝土达到峰值压应力时对应的应变,为此时的纵筋应变[11]。再根据纵筋单轴加载时的应力-应变本构关系曲线,得到此时纵筋应变对应的应力,从试验数据中扣除纵筋应力的影响,即可得到真正的约束混凝土峰值压应力。
钢筋单轴加载的本构关系曲线模型,有明显屈服点的钢筋采用三段式模型,无明显屈服点钢筋采用两段式模型,见图2。

图2 钢筋本构关系曲线Fig.2 Constitutive relations of steel bars
有屈服点钢筋,采用三段式模型:线弹性阶段、屈服阶段和硬化阶段。计算公式[1]为
(5)
式中:εs为钢筋应变;εy是钢筋屈服强度fy对应的屈服应变;εuy是钢筋硬化起点的应变;εu是钢筋极限强度fu对应的极限应变;η为钢筋硬化段斜率,η=(fu-fy)/(εu-εy)。
无屈服点钢筋,采用两段式模型:线弹性阶段及硬化阶段。计算公式[1]为
(6)
式中:εe为钢筋在比例极限fe对应的应变;η为钢筋硬化段斜率,η=(fu-fe)/(εu-εe)。
1.2.4 非约束混凝土峰值压应变处理方法
为避免计算方法的差异产生的误差,本文采用文献[12]中模型对非约束混凝土峰值压应变的处理方法,计算公式为
εco=0.000 5(fco)0.4
(7)
1.2.5 体积配箍率计算方法
数据库中试件的箍筋形式符合“同心对称”原则,本文按照文献[13]的方法计算体积配箍率,见表2。

表2 各箍筋形式的体积配箍率计算方法Tab.2 Calculation methods of volumetric ratio for different stirrup configurations
1.3 数据库试验数据处理方法
为了提高研究结果的准确性,本文按照以下原则进行收集数据:约束混凝土柱中,箍筋均只有一层;试件的高宽比范围均在2~6;试验数据均是在试件轴心受压作用下得到的。
为建立约束混凝受压应力-应变曲线数据库,本文搜集326个约束混凝土柱的轴压应力-应变关系曲线数据,376个约束混凝土试件峰值压应力试验数据及376个约束混凝土试件峰值压应变试验数据,数据库中涉及的箍筋形式见图3。对数据库试验数据,按照本章中的计算方法进行处理,数据见表3、4。
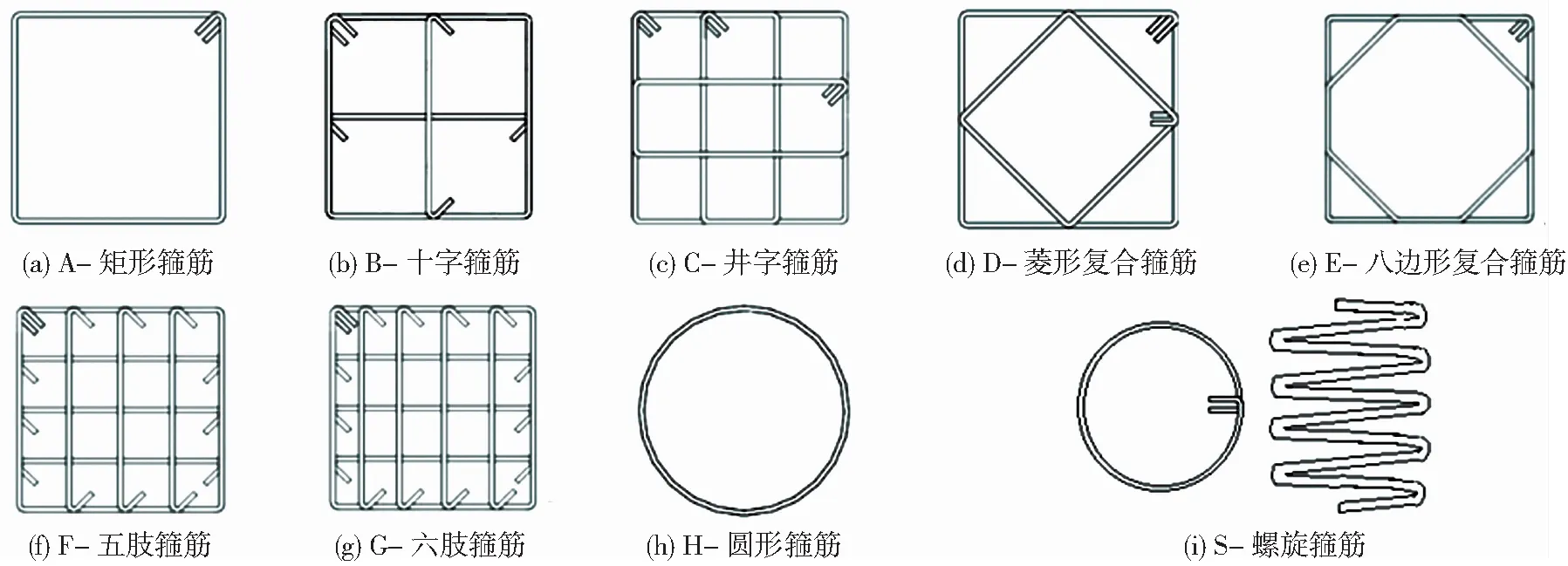
图3 箍筋形式Fig.3 Stirrup configurations
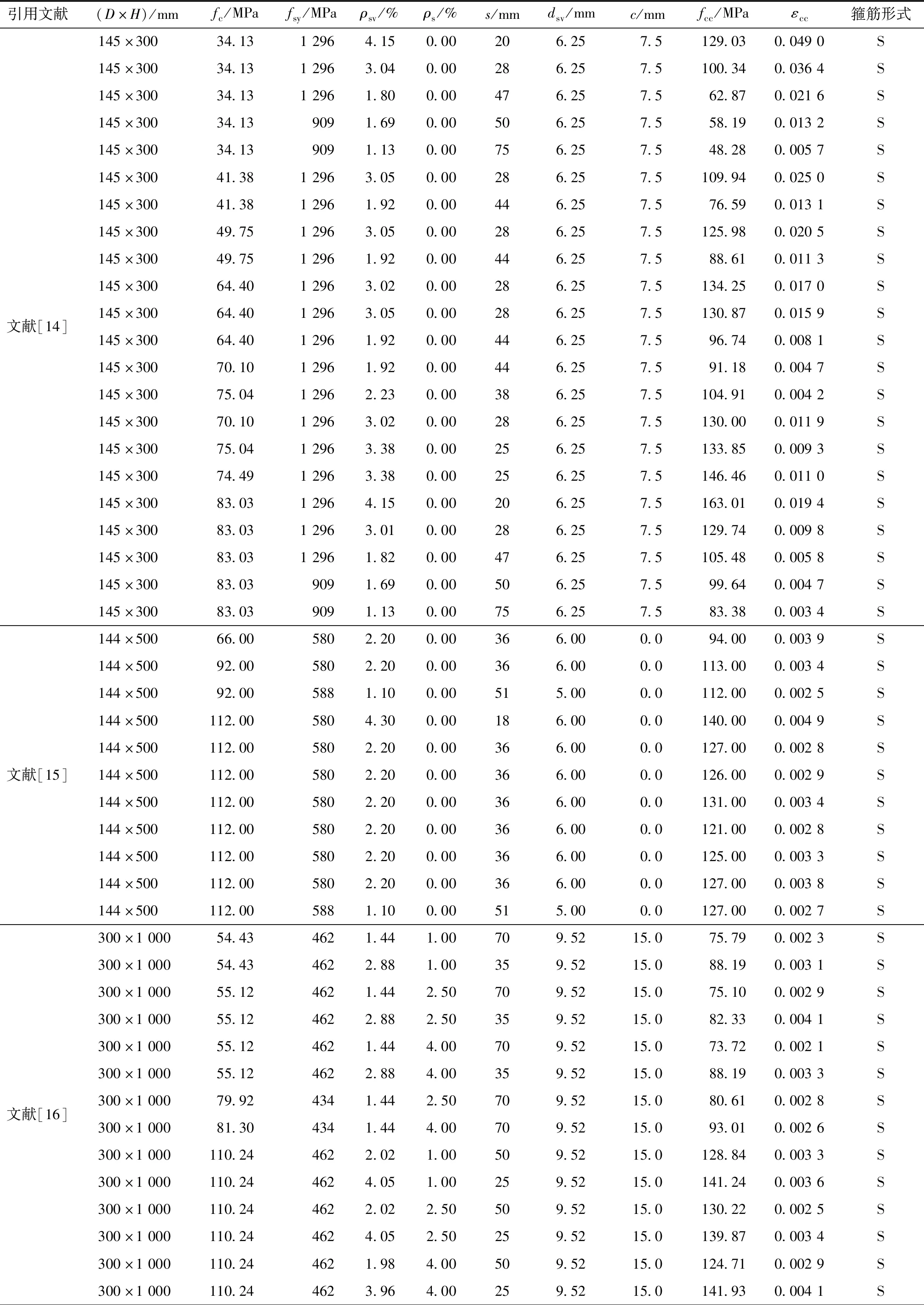
表3 圆形箍筋及螺旋箍筋约束混凝土圆柱试验数据Tab.3 Experimental results of concrete columns confined by circular and spiral stirrups
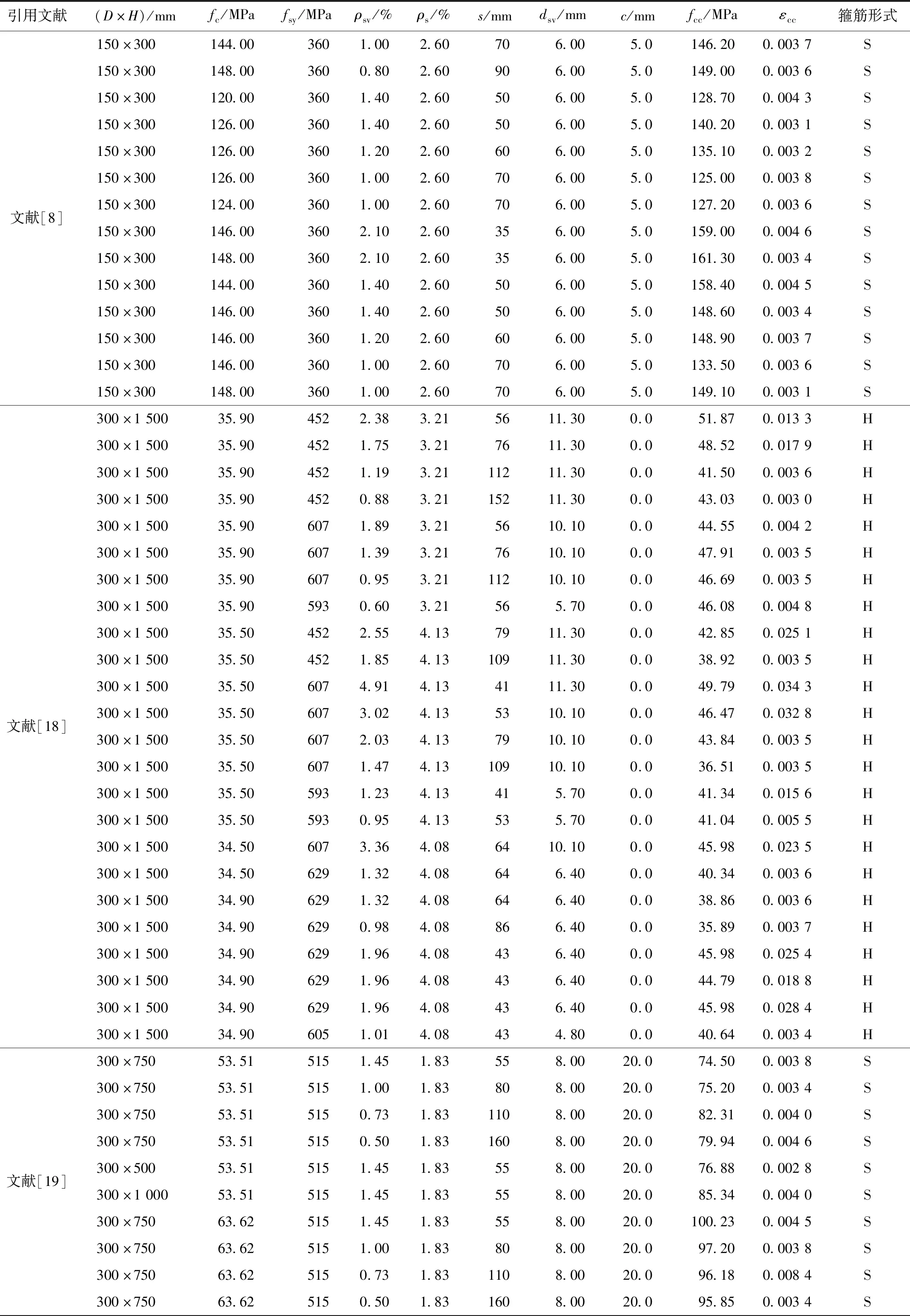
续表3

续表3
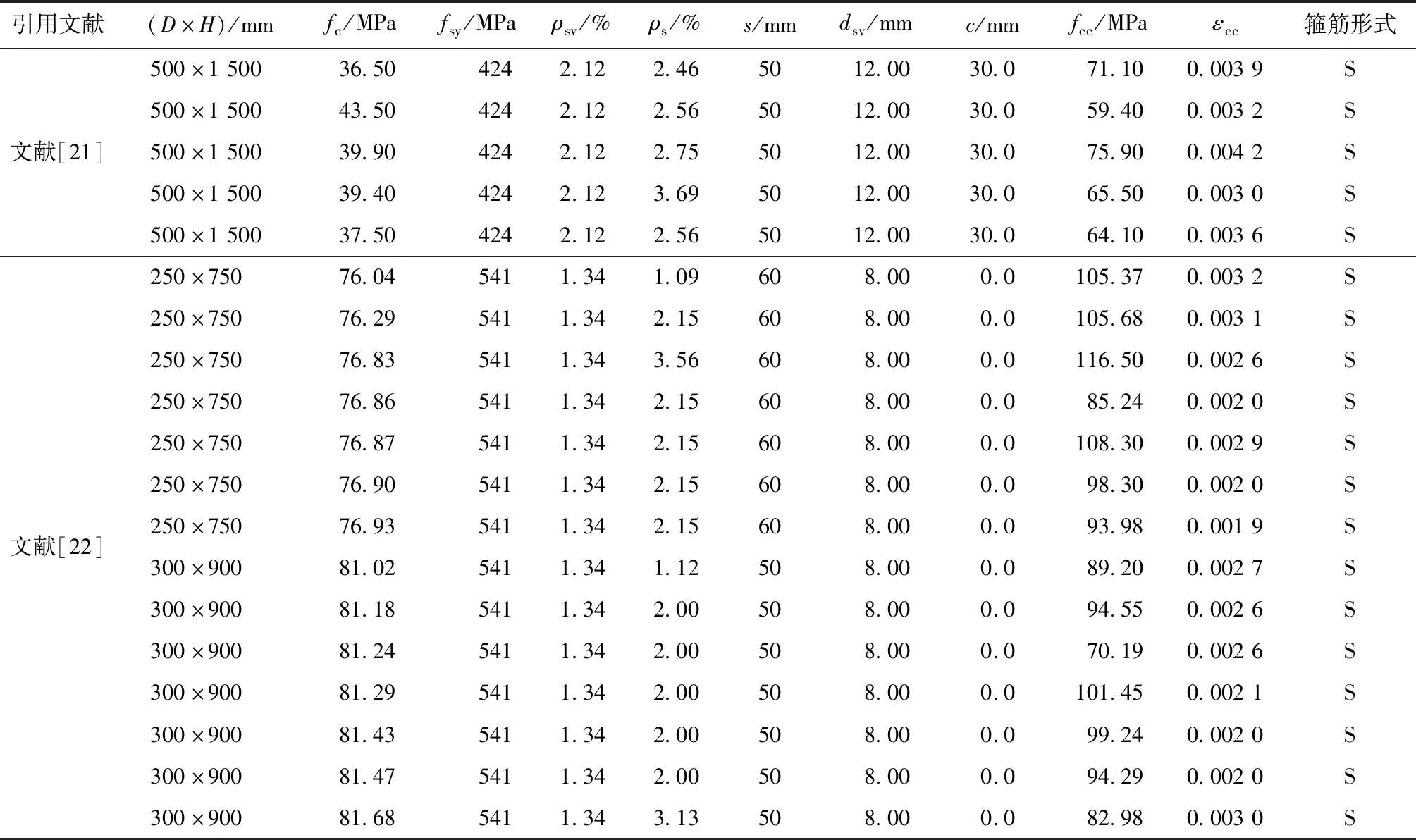
续表3

表4 箍筋约束混凝土矩形柱试验数据Tab.4 Experimental results of square concrete columns confined by stirrups
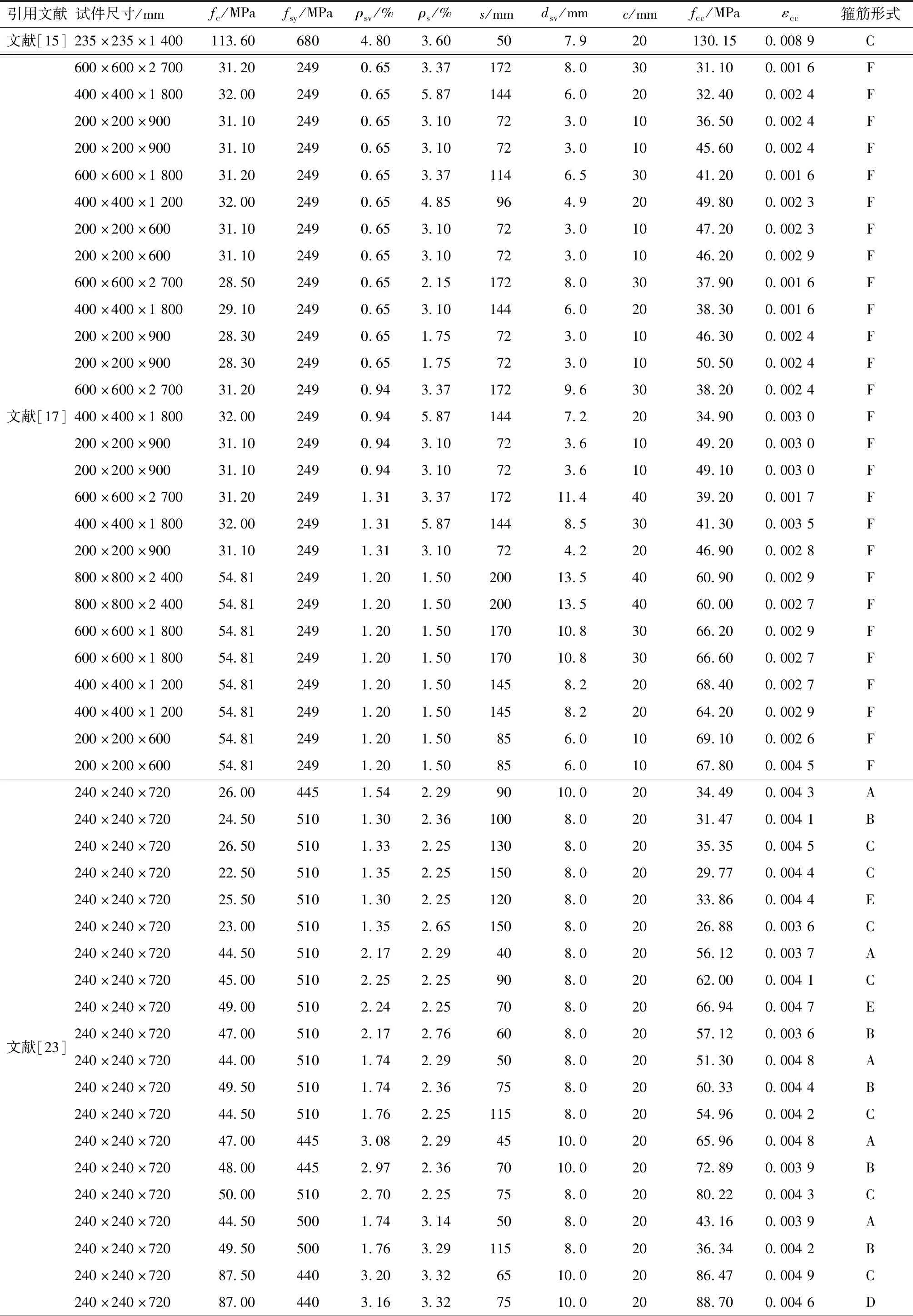
续表4
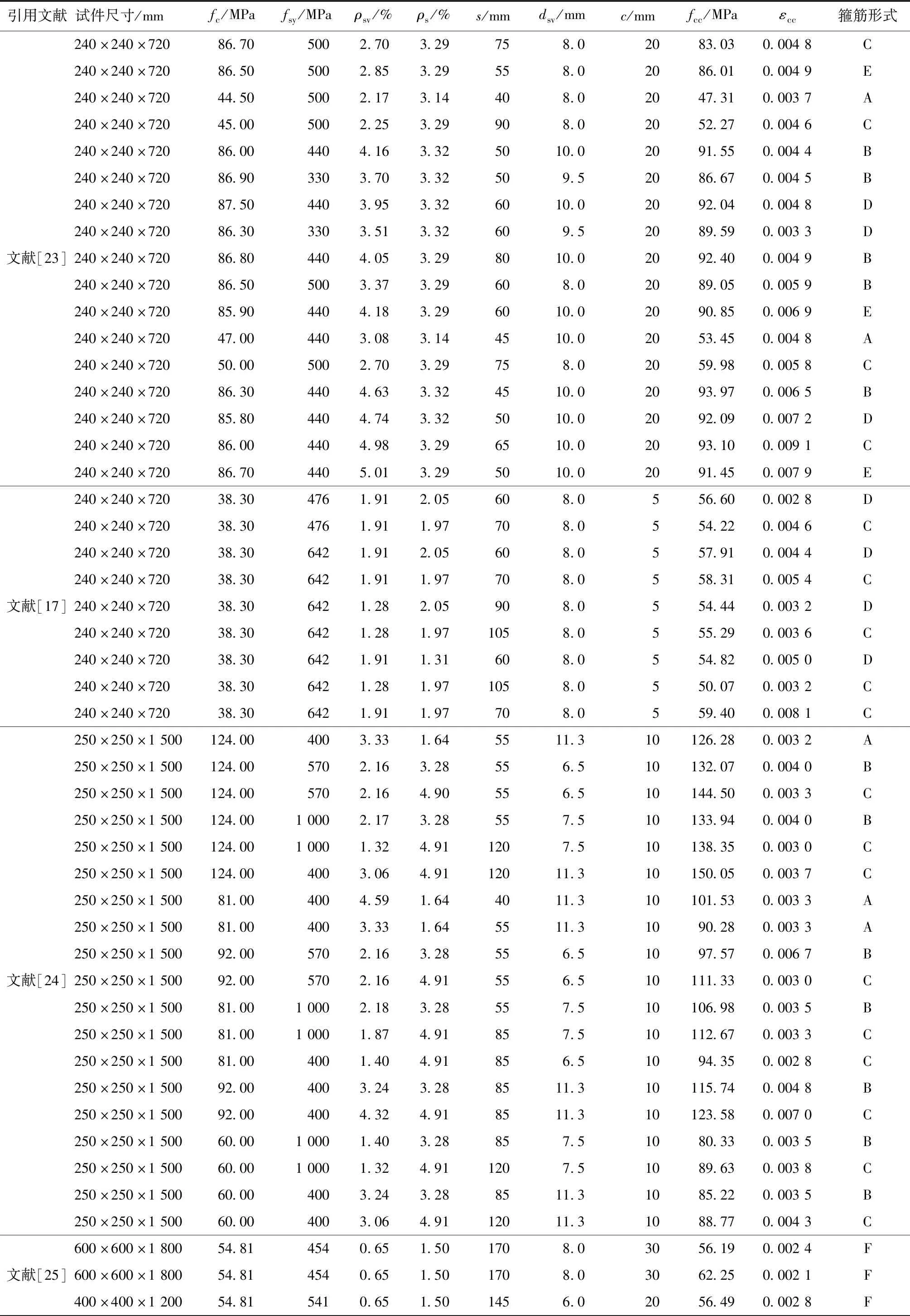
续表4
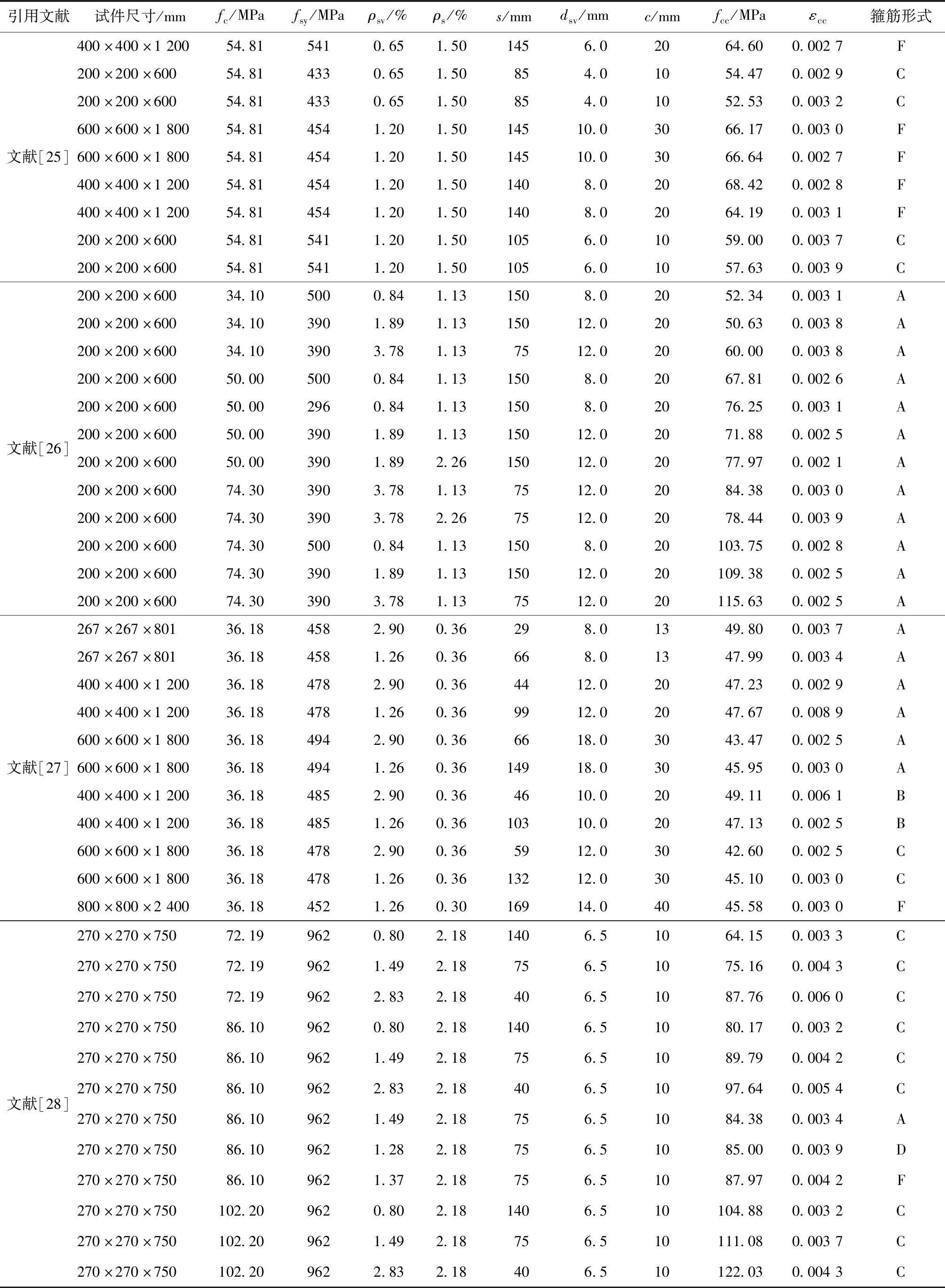
续表4
2 关键参数对约束混凝土柱受力性能影响分析
研究各因素对约束混凝土强度增强系数(Kc=fcc/fc)和变形增强系数(Kε=εcc/εc)的影响,分析原因。
2.1 混凝土强度
图4是强度增强系数和变形增强系数随混凝土强度的变化[5,14-15,17,19,30]。
由图4(a)和图4(b)可知,同一研究中,随着混凝土强度增加,约束混凝土强度增强系数和变形增强系数减小。当混凝土强度较高时(fc>90 MPa),强度增强系数均小于1.5。这主要是由于随着非约束混凝土强度增加,其横向扩展变形能力降低,箍筋对混凝土的约束能力随着混凝土强度的增加而减小。因此,为了提高高强混凝土的强度增强系数和延性增强系数,需要增加约束。
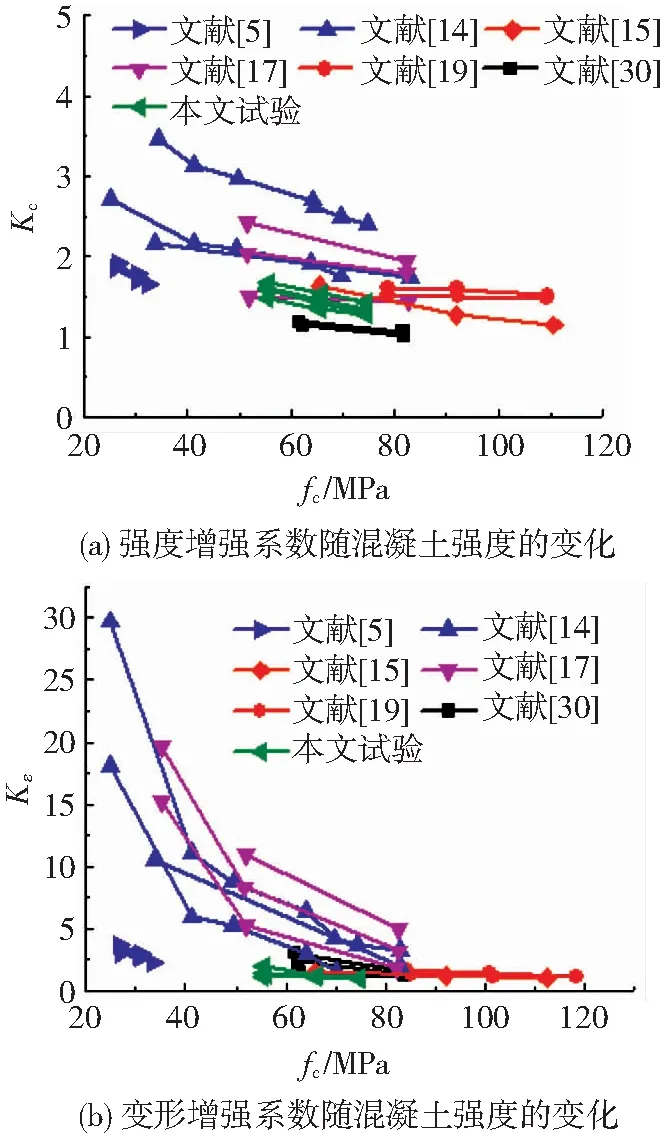
图4 混凝土强度对试件强度和变形的影响Fig.4 Influence of concrete strength on deformation and strength of specimens
2.2 箍筋屈服强度
箍筋屈服强度是影响约束混凝土强度和变形的主要参数之一。图5是强度增强系数和变形增强系数随箍筋屈服强度的变化[5,11,14,16-17,20,30-31]。当箍筋在约束混凝土的峰值应力处达到屈服强度,高强度箍筋可以有效提高约束混凝土的强度和变形能力。若箍筋在约束混凝土的峰值应力处没有达到屈服强度,提高箍筋屈服强度,无法增强约束效果。因此,单纯提高箍筋强度并不能保证箍筋对整体试件的约束效果显著提高,需要综合考虑体积配箍率,混凝土强度等因素。
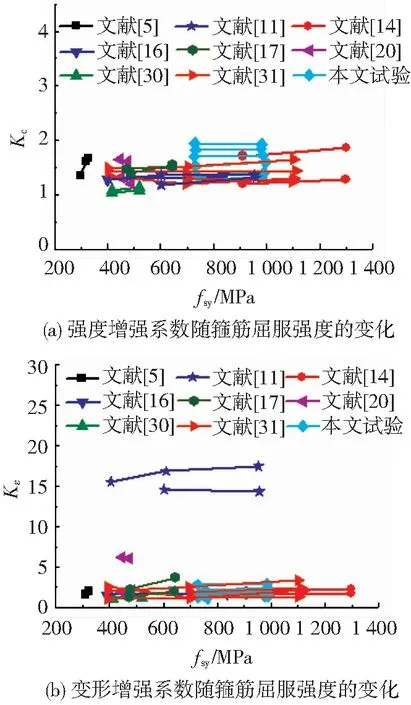
图5 箍筋屈服强度对试件强度和变形的影响Fig.5 Influence of stirrup yield strength on deformation and strength of specimens
2.3 体积配箍率
箍筋的体积配箍率由箍筋间距、箍筋直径和核心混凝土尺寸决定。高体积配箍率能够抵抗较大的应力,为核心混凝土提供较大的有效约束约束,提高约束程度。图6给出了约束混凝土的强度增强系数和延性增强系数随体积配箍率的变化[5,8,14-18,20,32]。当体积配箍率大于1.5%时,约束混凝土的强度增强系数迅速增加。此外,在体积配箍率小于1%时,对约束混凝土试件强度的增强作用较小。在图6(b)中,当体积配箍率为1.0%~4.0%时,约束混凝土变形增强系数增长迅速。由此可见,在设计箍筋的体积配箍率时至少应大于1%。

图6 体积配箍率对试件强度和变形的影响Fig.6 Influence of volumetric ratio on deformation and strength of specimens
2.4 箍筋间距
图7是约束混凝土强度增强系数和变形增强系数随箍筋间距的变化规律[17,26,28,33-36]。由图7可知,箍筋间距越小,试件强度和变形能力越好。在其他条件相同的条件下,箍筋间距过大,对核心混凝土无法提供有效的约束,约束混凝土试件的强度和变形能力都没有明显提高。当箍筋间距大于150 mm,箍筋间距的变化对约束混凝土柱强度和变形能力的影响基本不再发生变化。此时箍筋能提供的约束效果较小,对约束混凝土柱的强度和变形能力作用不大。箍筋间距减小时,相邻两箍筋间被有效约束的混凝土面积增加,这样可以显著提高约束混凝土柱的强度,较好地改善柱子的变形能力。
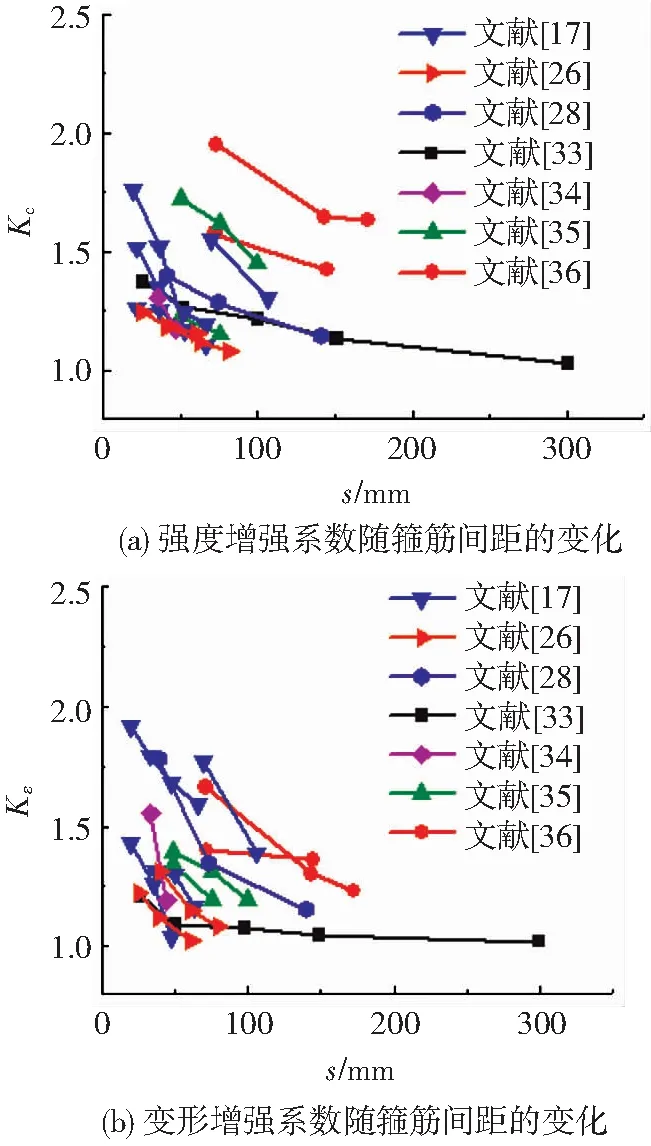
图7 箍筋间距对试件强度和变形的影响Fig.7 Influence of stirrup spacing on deformation and strength of specimens
2.5 纵筋配筋率
纵筋对试件核心区混凝土的峰值压应变产生较大影响,对峰值压应力有一定作用,特别是约束高强度混凝土柱中配置纵筋,有利于提高柱子的变形能力[6,24]。图8是约束混凝土强度增强系数和变形增强系数随纵筋配筋率的变化规律[5,16,21,26,30,37]。由图8(a)可知,约束混凝土的强度增强系数随着纵筋配筋率的增大提高。在图8(b)中,约束混凝土变形增强系数,随着纵筋配筋率增加有所提高。Kim[16]的研究中,由于试件混凝土强度大,体积配箍率小,纵筋与箍筋强度小,能提供的约束作用有限,出现了个别试件变形增强系数仅为1.0左右的情况。纵筋配筋率对约束混凝土柱强度和变形能力的影响不可忽略。
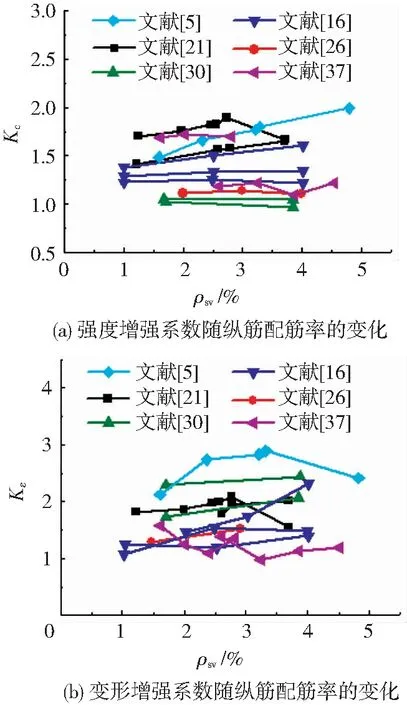
图8 纵筋配筋率对试件强度和变形的影响Fig.8 Influence of longitudinal reinforcement ratio on deformation and strength of specimens
2.6 箍筋形式
圆形柱箍筋形式主要有圆形箍筋和螺旋箍筋。表5中列举了分别采用圆形和螺旋箍筋试件的部分试验结果。其他条件相同或接近的情况下,圆形箍筋为约束混凝土柱提供更好的约束效果,试件有更好的强度和变形能力。这是由于圆形箍筋都是独立的,当其中一个发生破坏时,其余箍筋继续提供约束力。因此,宜使用圆形箍筋来设计试件。
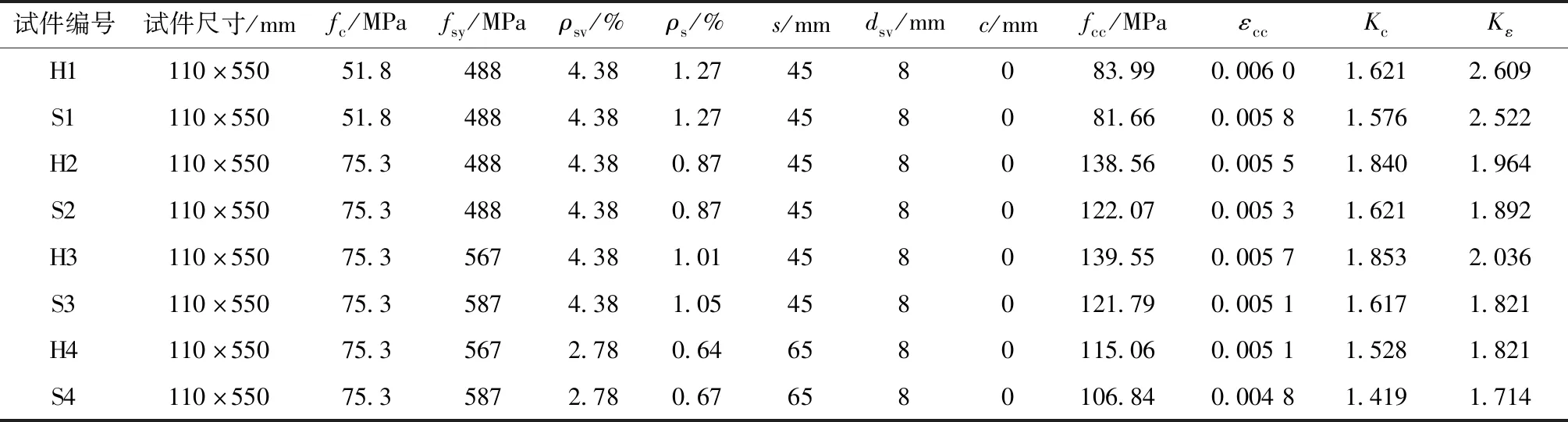
表5 其他条件相同时,圆形箍筋和螺旋箍筋对Kc、Kε的影响Tab.5 Influence of stirrup configuration on Kc and Kε
对于矩形柱,箍筋形式决定了试件水平方向的有效约束面积和纵向钢筋的分布,影响核心混凝土水平方向的有效约束面积。表6是不同箍筋形式对试件强度增强系数和变形能力增强系数的影响规律[10,23,25,27,38]。复杂的箍筋形式约束效果明显好于单个矩形箍。箍筋形式B和D的约束效果相近,网格式箍筋形式C、F、G,能增强约束混凝土柱的强度和变形能力,网格划分越密集,约束效果越好。从箍筋约束效果及施工复杂程度的角度出发,对于矩形柱,避免使用箍筋形式A(矩形箍),建议采用B(十字复合箍)或C(井字箍)两种箍筋形式。
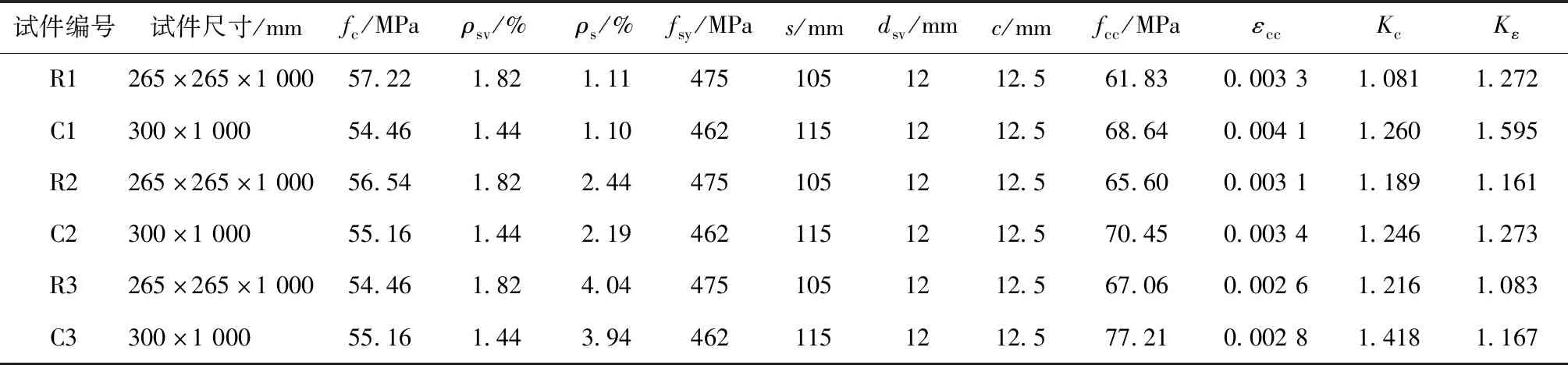
表6 其他条件相同或接近时,圆形截面与矩形截面对Kc、Kε的影响Tab.6 Influence of cross section on Kc and Kε
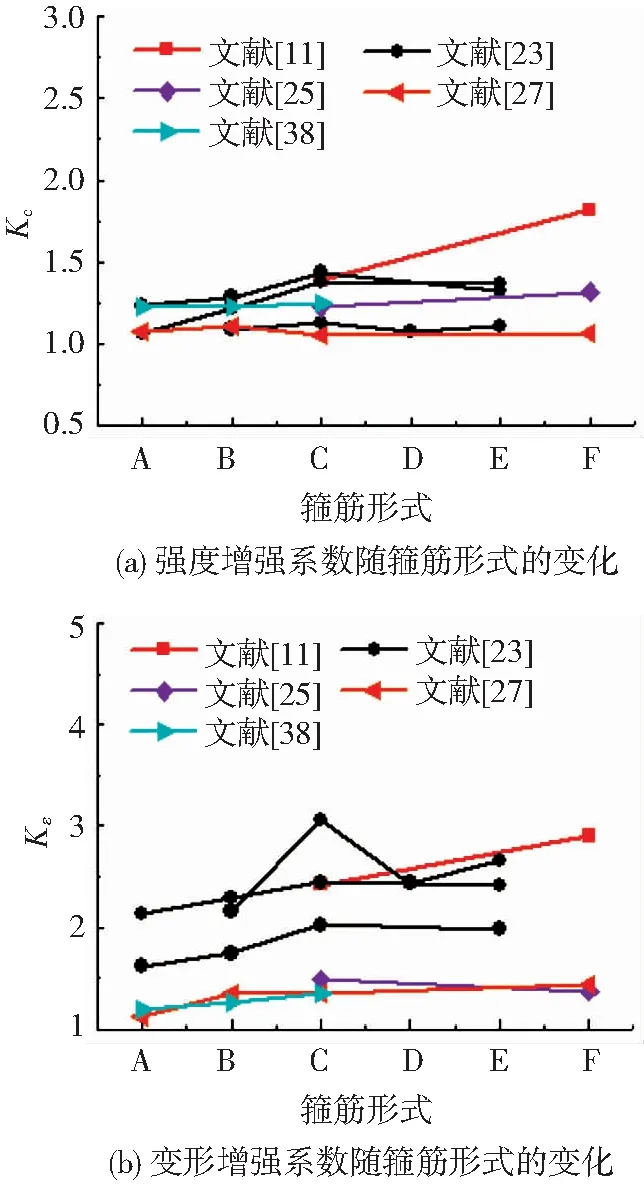
图9 箍筋形式对试件强度和变形的影响Fig.9 Influence of stirrup configuration on deformation and strength of specimens
2.7 试件截面形状与尺寸
在混凝土强度、试件截面面积、纵筋配筋率及体积配箍率相同或接近的条件下,圆形箍筋或螺旋箍筋形式要比矩形箍筋对混凝土的约束效果好。图10中列举的曲线,是在其他条件相同或接近的情况下,约束混凝土圆柱和矩形柱试件受压应力-应变曲线对比。由图可知,在其他条件相同的情况下,圆形截面柱的承载能力及变形能力优于矩形截面柱。
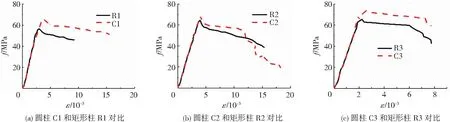
图10 其他条件相同或接近时,约束混凝土圆柱和矩形柱受压应力-应变曲线对比Fig.10 Comparison of compressive stress-strain curves of different confined concrete columns
在研究约束混凝土受压应力-应变曲线时,试件的尺寸效应不能忽略。符佳等[25]引入尺寸效应影响系数。试件高宽比相同时,截面尺寸越大,配箍率越低,受压时试件越容易破坏。通常采取较高体积配箍率和高强箍筋来增强试件的约束效果。在其他条件均相同情况下,由于尺寸效应的存在,大尺寸试件的强度增强系数(Kc)和变形增强系数(Kε)通常小于小尺寸试件,见表7。分析原因认为,一方面是由于箍筋约束作用是通过对核心区受弯和受拉作用来完成的,小尺寸试件箍筋主要是受拉破坏,大尺寸试件主要是受弯破坏[22],其约束应力要小,相应的约束混凝土强度和变形能力都较低;另一方面是由于大尺寸截面的构件在角部产生的应力集中要比小尺寸截面的构件严重,且在其他条件相同的情况下,大截面面积构件体积配箍率要小于小截面面积构件。
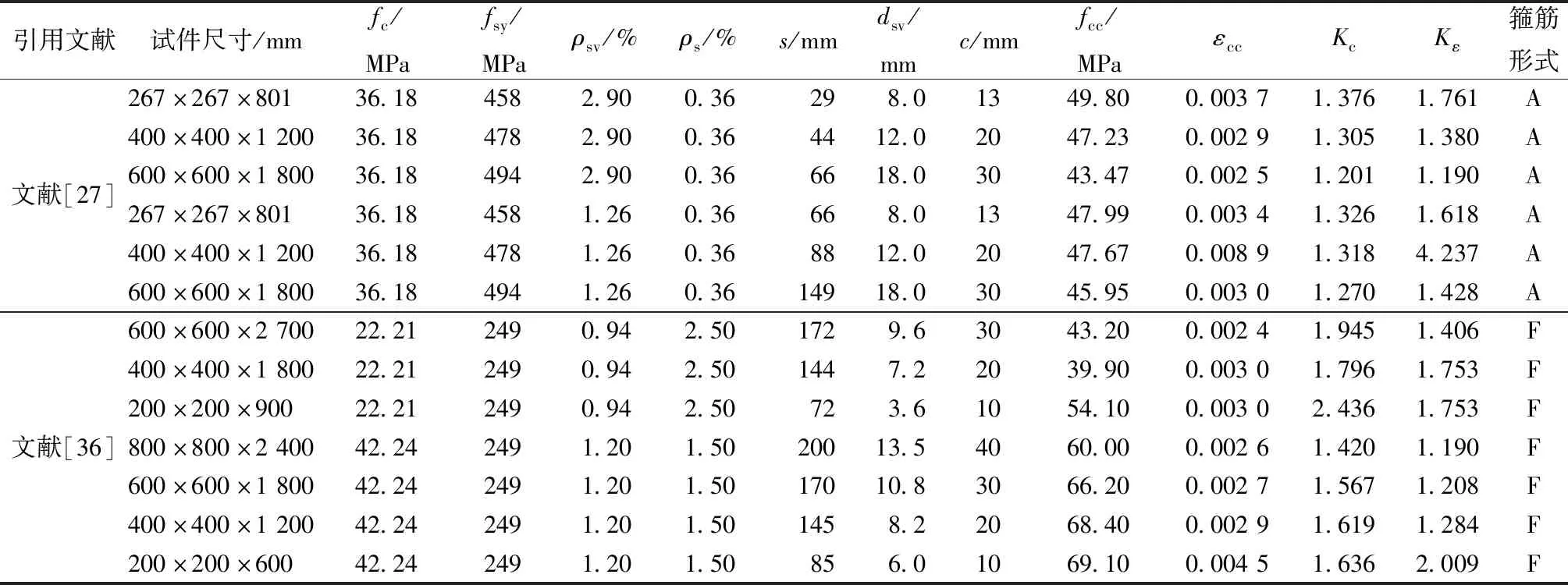
表7 其他条件相同或接近时,试件尺寸对Kc、Kε的影响Tab.7 Influence of size effect on Kc and Kε
3 约束混凝土受压应力-应变曲线统一方程
3.1 约束混凝土受压应力-应变曲线统一方程的建立
为了描述该应力-应变关系曲线统一方程,曲线采用无量纲坐标,x=ε/εcc,y=f/fcc。由于文献[5]中Mander模型对约束混凝土本构关系曲线上升段预测较准确,统一方程上升段直接采用Mander模型来描述。上升段公式为
(8)
式中γ是控制上升段曲线的参数,由式(9)计算
γ=Ec/[Ec-(fcc/εcc)]
(9)
式中Ec为非约束混凝土初始弹性模量
统一方程下降段以文献[2]中过镇海模型下降段为基础,建立统一方程下降段公式。统一方程下降段为
(10)
式中α和β是下降段曲线的重要参数,决定了该公式的预测效果。本文采用回归分析的方法来确定α和β的计算公式。
本文用无量纲坐标描述曲线,x>0,0≤y≤1,采用Mander与过镇海的组合的形式来描述统一方程,能够满足约束混凝土本构关系曲线的特性:1)曲线通过坐标初始点,即x=0时,y=0;2)从坐标初始点开始的切线斜率可以表述为dy/dx=Ec/Eco;3)上升段曲线满足0≤x≤1时,d2y/d2x<0;4)在曲线峰值点(εcc,fcc)处的切线近似为水平直线,即x=1时,y=1且dy/dx=0;5)下降段曲线中存在一个拐点,即x>1时,d2y/d2x=0;6)下降段曲线中存在一个最大曲率点,即x>1时,d3y/d3x=0;7)当应力无穷大时,曲线应力趋近于0,即x→∞,y→0,dy/dx→1。
3.1.1α计算公式
约束混凝土的应力-应变曲线关系的变化,不仅与非约束混凝土强度、体积配箍率、箍筋屈服强度有关,还与箍筋间距、纵筋配筋率以及试件截面尺寸存在一定关系。此处试件截面尺寸为圆柱截面直径或方柱截面边长,用符号D表示。分析各影响因素对α的影响,以此为基础,提出α回归分析模型。
图11中各图为其他条件相同或接近时,α随某一影响因素的变化规律。由图11 (a)可知,随着非约束混凝土强度的提高,α呈下降趋势,但fc<80 MPa时,该现象不明显。这是由于试件体积配箍率和箍筋强度存在较大差异,对核心混凝土的约束效果差异明显,导致α的变化规律不明显。由图11(b)和(c)可知,随着体积配箍率和箍筋屈服强度的提高,α呈增大趋势。根据已有文献的研究,发现核心混凝土的横向扩张程度不仅与体积配箍率、箍筋屈服强度有关,而且受非约束混凝土的强度影响。在一定范围内,被约束混凝土强度较低,体积配箍率和箍筋屈服强度较高时,试件被压碎时,核心混凝土部分横向扩张程度较大,试件延性较好。引入约束效果相关系数η,η=ρsvfsv/fc,其中,fsv是约束混凝土达到峰值压应力时箍筋达到的应力水平。综合反映体积配箍率、箍筋屈服强度和非约束混凝土强度对参数α的影响。分析发现,α0.5随约束效果相关系数η的变化规律较明显,见图11(d)。随着约束效果相关系数η的增大,α0.5先迅速下降之后趋近于0.92,呈幂函数变化规律。由图11(e)中可知,α与纵筋配筋率ρs呈正相关关系,随着纵筋配筋率的增加,α呈明显的线性增加趋势。图11(f)~(g)中是箍筋间距s与试件截面尺寸D对参数α的影响规律,随着箍筋间距的增大,参数α呈下降趋势;试件截面尺寸D越大,参数α越大,但增加程度减小。参数α随箍筋间距与试件截面尺寸变化的规律性并不十分明显,这是因为箍筋间距与试件截面尺寸会影响试件水平面内有效约束面积的大小,且通常与箍筋间距呈负相关,与试件截面尺寸呈正相关。定义箍筋间距s与试件截面尺寸D的比值(s/D)为有效约束面积影响系数,经分析发现,α0.5与有效约束面积影响系数s/D,有较强的规律性,α0.5与s/D线性相关,α0.5随s/D增大而减小。
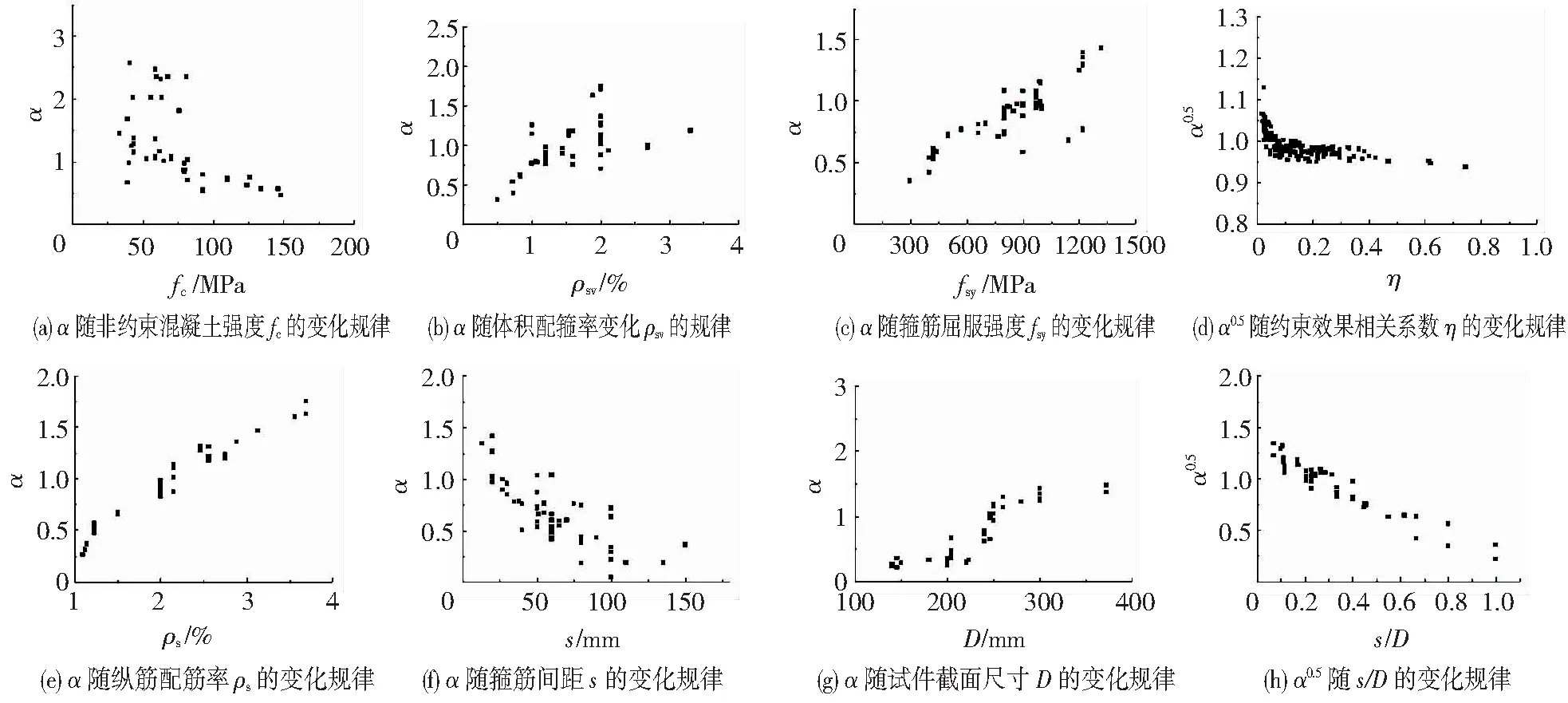
图11 α随各影响因素的变化规律Fig.11 Influence of parameters on α
基于α随各影响因素变化规律的分析,建立α的回归分析模型
(11)
回归分析发现,参数α随非约束混凝土强度的变化产生波动,在fc>80 MPa时,参数α的拟合值偏小,fc<80 MPa时,参数α的拟合值偏大,增加一个混凝土强度影响系数r,r=80 MPa/fc,得到α的计算公式为
(12)
式中fsv为约束混凝土达到峰值压应力时的箍筋应力水平,由式(3)和式(4)计算。
该公式R2=0.916 3,标准差是0.006 5,平均绝对误差是0.005 0,说明拟合效果较好。
3.1.2β计算公式
基于对参数α的研究,分析其他条件相同的情况下,β分别随约束效果相关系数、有效约束面积影响系数和纵筋配筋率的变化规律,见图12。
图12中各图为其他条件相同或接近,β随某一影响因素的变化规律。由图12可知:1)一定范围内,η越大,β越小,且线性变化较明显,见图12(a)。究其原因,约束效果相关系数η较大时,箍筋对核心混凝土的约束效果提高,试件受压应力-应变曲线下降段较平缓,此时参数β较小。2)由图(b)知,一定范围内,有效约束面积影响系数越小,箍筋间距越小试件截面尺寸越大,参数β越小,试件延性发展越好。3)由图(c)知,参数β与纵筋配筋率ρs呈正相关关系,随着纵筋配筋率的增加,β呈明显的线性增加趋势。
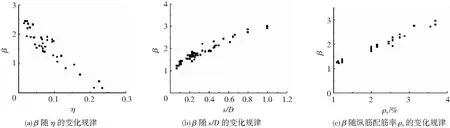
图12 β随各影响因素的变化规律Fig.12 Influence of parameters on β
基于参数β随η、s/D和ρs变化规律的分析,建立β的回归分析模型
(13)
回归分析发现,在fc>80 MPa时,参数β的拟合值偏小,fc<80 MPa时,参数β的拟合值偏大,引入混凝土强度影响系数r,r=80 MPa/fc,能明显增强参数β的拟合效果。本文得到β的计算公式为
(14)
该公式R2=0.920 1,标准差等于0.003 9,平均绝对误差等于0.002 7,R2接近1,标准差与平均绝对误差接近0,说明拟合效果较好。
图13是参数α和参数β的拟合效果图,图中可以看出参数α和参数β计算公式具有较好的拟合效果。
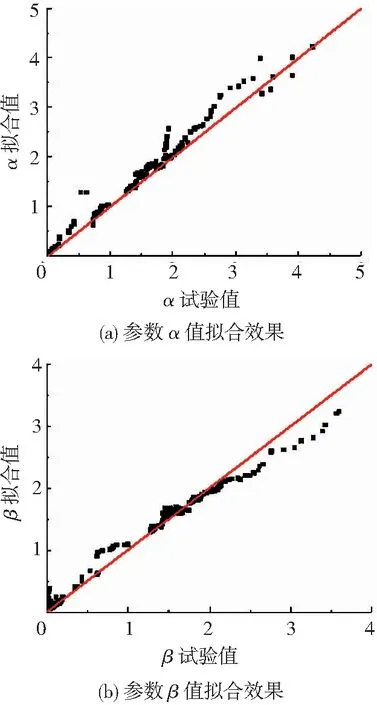
图13 α与β拟合效果Fig.13 Fitting curves of α and β
3.1.3 本文统一方程模型分析验证
为了进一步验证本文统一方程的精确度,用统一方程和已有的受压应力-应变模型,对本课题组试验得到的试验结果,进行了计算。各模型及本文模型对部分试件的计算结果和试验结果的比较,见图14。
由图14可知,由本文统一方程得到的预测曲线和试验曲线的吻合程度均好于已有模型。分析原因认为是:1)每一种模型都是在各自的试验基础上提出的,混凝土材料离散性大,试验方法与测量手段又不统一,模型在计算fcc、εcc、ε80时误差较大。2)模型中所考虑的影响因素是否全面,是下降段延性好坏的关键[31]。Li Bing模型未考虑试件达到峰值压应力时箍筋的应力水平,且每个试验曲线的参数β是用试验法和误差法得来的,对预测试件应力-应变曲线会产生较大误差。3)模型建立的试验基础广泛与否对模型模拟是否准确起着重要作用。本文统一方程考虑的影响因素比较全面,且范围较广,这也是本文模型下降段延性较好的一个主要原因。本文提出的分析模型精确度较高,适用范围更广,计算结果是精确可信的。

图14 各模型及本文模型与本文试验曲线对比Fig.14 Comparison of different models
3.2 峰值压应力
采用Richard公式[39]的形式,引入参数kc,定义kc=pη,kc与约束效果相关系数有关,而且受纵筋配筋率和箍筋体积配箍率的影响。回归分析得到峰值压应力计算公式
(15)
式中:η为约束效果相关系数,η=ρsvfsv/fc;ρsv为体积配箍率;fsv为约束混凝土达到峰值压应力时箍筋的应力水平,由公式(3)计算;p为钢筋影响系数,p=(1+ρsv)/[3(1-ρs)];ρs为纵筋配筋率。
系数mc、nc按混凝土强度和试件截面形状划分,回归分析,得出mc、nc取值表,见表8。

表8 mc、nc取值表Tab.8 Values of mc and nc
由R2及残差平方和可知,该公式拟合效果较好。图15是本文提出的峰值压应力公式,对数据库试件峰值压应力的预测值,与试验值的对比图。本文公式的误差小。以绝对误差积分为指标,该公式的绝对误差积分为12.35%,精确度较高。
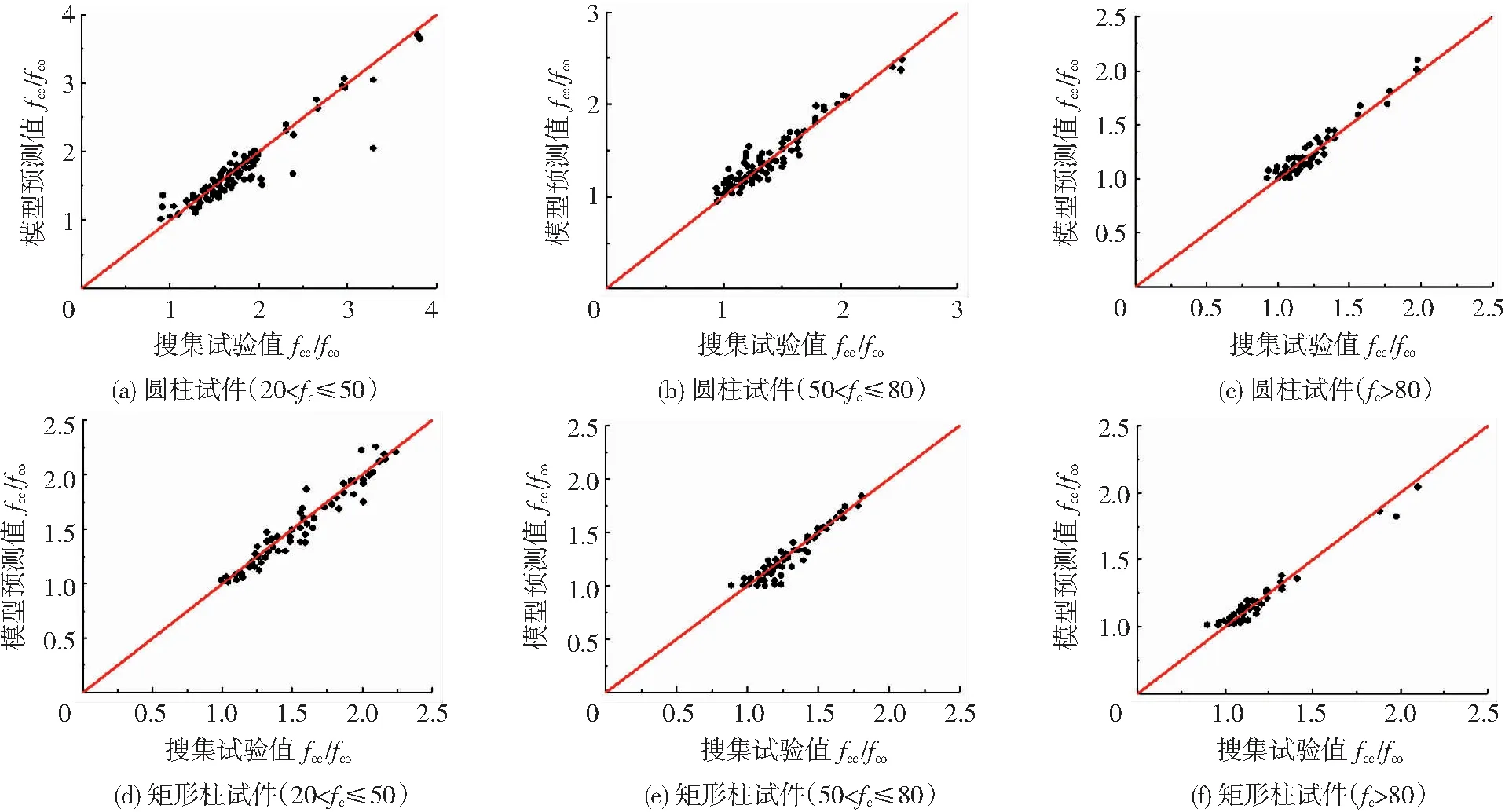
图15 本文公式的峰值压应力预测值与试验值对比Fig.15 Comparison of experimental values and calculated values of peak stress
3.3 峰值压应变
综合考虑约束混凝土影响因素,引入参数kε,定义kε=pη(3-1.1(s/Dcor)),Dcor为核心混凝土长度,回归分析得出峰值压应变计算公式为
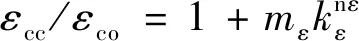
(16)
式中:εco为非约束混凝土的峰值压应变,按式(7)计算;参数mε、nε按混凝土强度和试件截面形式划分,回归分析得出mε、nε的取值表,见表9。

表9 mε、nε取值表Tab.9 Values of mε and nε
R2接近于1,相关关系强,残差平方和接近于0,数据分布较好,图16是本文提出的峰值压应变计算公式,对数据库试件峰值压应变的预测值,与试验值的对比图。从图中可以看出,本文峰值压应变计算公式,预测值与试验值之间误差小,绝对误差积分为13.21%,精确度较高。
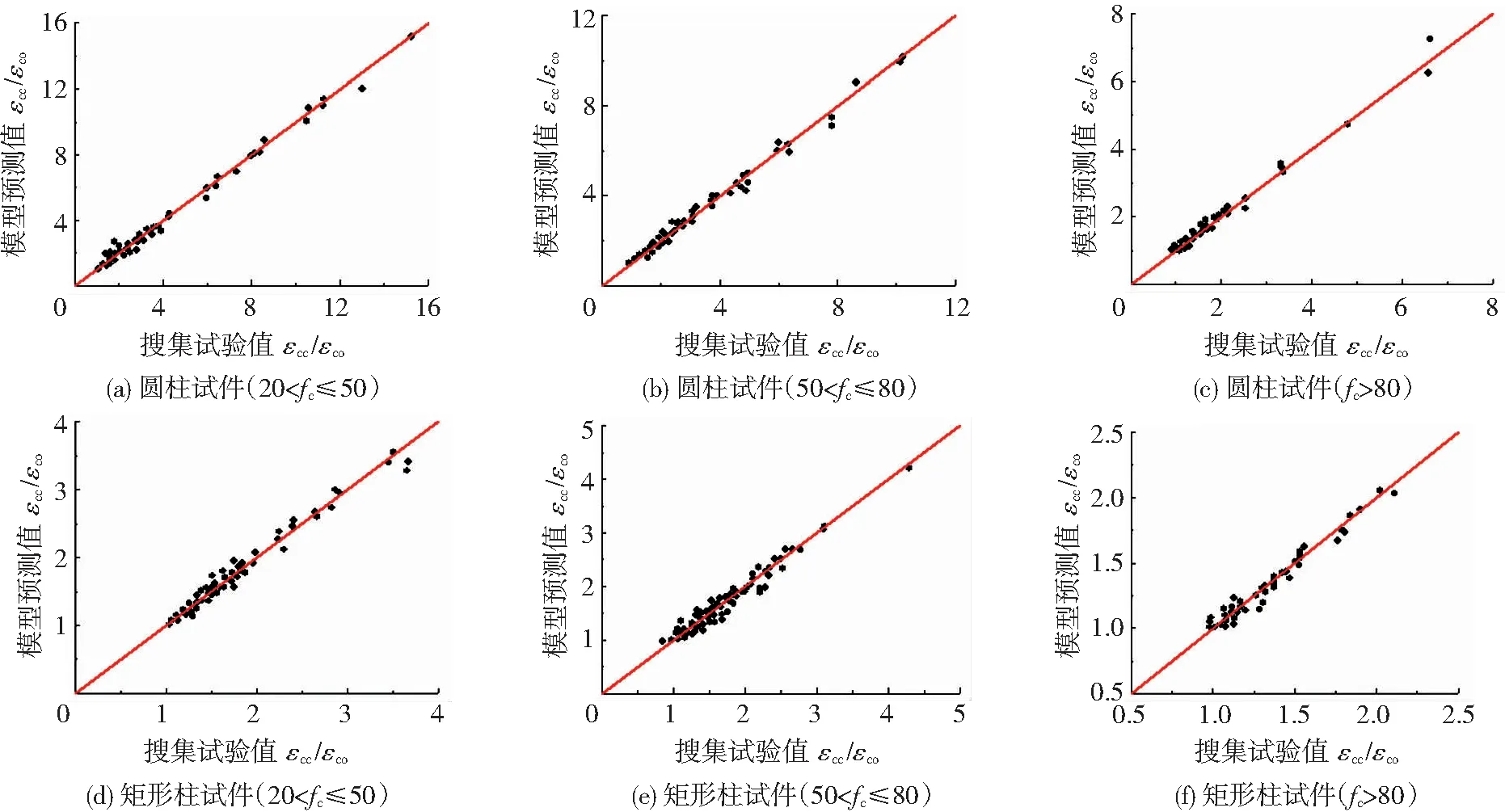
图16 本文公式的峰值压应变预测值与试验值对比Fig.16 Comparison of experimental values and calculated values of peak strain
4 结 论
1)建立数据库试验数据处理方法,包括混凝土保护层处理方法、约束混凝土达到峰值应力时箍筋应力计算方法、纵筋应力处理方法、非约束混凝土的峰值压应变处理方法及体积配箍率计算方法。
2)本文搜集326个约束混凝土柱的轴压应力-应变关系曲线数据,376个约束混凝土试件峰值压应力试验数据及376个约束混凝土试件峰值压应变试验数据,建立了约束混凝土本构关系数据库。
3)基于Mander模型和过镇海模型,建立了约束混凝土受压应力-应变曲线统一方程。对数据库试验数据进行对比分析,结果表明,本文统一方程的预测曲线与试验曲线吻合较好,准确性较高,适用范围更广。
4)本文基于Richard公式的形式,提出了峰值压应力和峰值压应变计算公式,定义了参数kc、kε。利用本文得出的计算公式,对数据库试验数据进行对比分析。结果表明,本文公式预测误差控制在15%以内,预测结果精确度较高,适用范围更广。