灰色GM(1，1)模型在上饶市用水需求预测中的应用研究

孙 璟，詹青宇

(1.上饶市水文局，江西 上饶 334000；2.铅山县水利局，江西 上饶 334500)

水是生命之源，是基础性的自然资源和战略资源，是地球上一切生物赖以生存和发展的物质基础，是生态系统最活跃的控制性要素。随着国民经济的发展和水资源供求状况的变化，人类对水资源的需求不断增加，导致其过度开发造成污染，供需矛盾日益突出，如今水资源短缺已成为我国经济发展的重要制约因素。随着最严格的水资源管理制度的实行，严格水资源管理的“三条红线”的限制，加强对水资源的依法管理，合理开发利用和保护水资源，实现水资源的可持续发展，已成为我国经济和社会发展的战略问题。因此，如何对有限的资源进行合理的开发利用，使之在可持续发展前提下发挥出最大的效用成为人类社会面临重要问题。

对用水结果进行模拟与预测，目前最常用的方法主要有GM(1，1)模型、BP神经网络和偏最小二乘回归与支持向量机藕合等。其中灰色GM模型最早是由邓聚龙教授于1982年提出的预测模型。灰色GM(1，1)模型在预测方法上，因其建模所需信息少，运算简单，易于检验，因此常被运用于解决不确定性的预测问题。经过三十多年的发展，被广泛应用于能源、生产、设计等各个领域[1]。但传统的模型在原理上存在固有缺陷，为模型的改进留下了大量的空间，从而涌现出大量的改进算法及应用[2-3]。

本文在GM(1，1)灰色模型的基础上，对上饶市需水趋势进行研究，分析农业、工业、生活和生态环境用水量组成的用水结构的变化规律，预测其用水需求，为上饶市水资源合理开发利用提供参考依据。

1 研究区用水结构概况

上饶市位于江西省东北部，简称赣东北。东邻浙江省衢州市，北毗安徽省池州市及黄山市，南依武夷山脉与福建省南平市相连。省内与景德镇、九江、南昌、鹰潭、抚州五市接壤。

上饶市水资源公报中用水数据从1997年开始收入，但因为农业用水波动较大，考虑建立模型更贴近实际情况的预测结果，本文采用2003—2018年公报中的用水量数据，将用水量分为农业、工业、生活、生态环境等四个部分，其中农业用水包括农田灌溉和林牧渔畜两部分，生活用水包括城镇居民用水、农村居民用水和城镇公共用水，具体数据见表1。

表1 上饶市各部门历年用水量及占比

由表1可以看出上饶市农业用水为用水大户，农业多年平均用水量占总用水量的77.33%，其次为工业用水，年均占总用水量的10.84%，各部门用水量整体呈上涨趋势。农业在2003—2008年是一个降低趋势，在2008—2013年之间呈现锯齿型上下浮动，随后呈上升趋势。农业用水受降水影响变化较大，其在丰水年份，用水量较小，在枯水年份年份用水量较大，同时随着经济飞速发展，城市发展的需要，农业灌溉模式的改变等一系列因素的共同作用。而工业、生活、生态环境用水量均受城镇化影响呈现不同幅度的增长，其中生活用水量的增长幅度尤为显著，如图1。

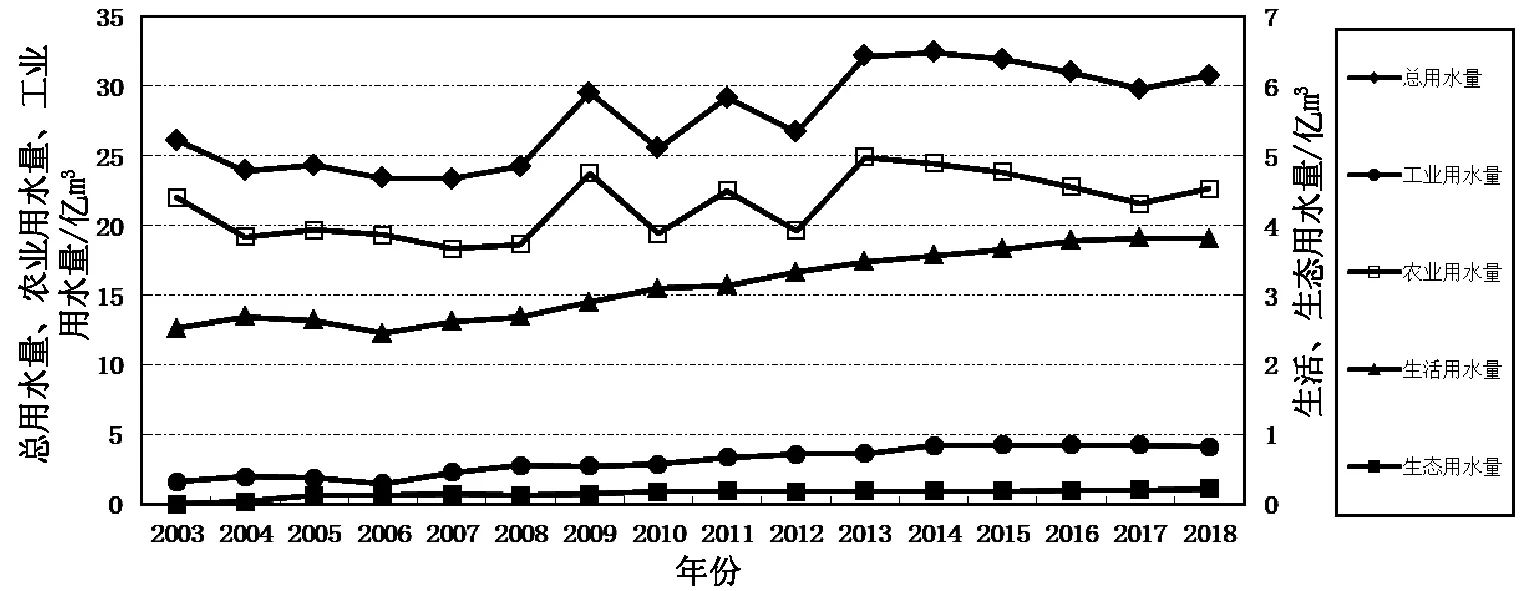
图1 上饶市各部门历年用水结构变化

2 模型建立、检验及预测

2.1 灰色系统微分方程GM(1.1)

灰色GM(1，1)模型在预测方法上[4-5]，因其建模所需信息少，精度高，能较好的反映实际状况，因此常常被应用在城市用水量预测中[6-9]。该模型就是利用已有年份的用水量数据与时间序列建立关系函数，通过关联分析对离散数据建立微分方程动态模型。通过对微分方程进行求解进而获得时间变量的响应函数，即获得用水量数据的预测模型。

将原始等间隔时间序列数据x(0)做一阶累加生成得到新的序，列x(1)，令z(1)为x(1)均值序列，其中

(1)

建立白化型GM(1.1)微分方程：

dx(1)/dt+ax(1)=u，

(2)

其中

(3)

(4)

求解微分方程可得预测模型：

y(1)(t+1)=[x(0)(1)-u/a]e-at+u/a， (t=1，2，3，…，n)，

(5)

式中a为发展系数，u为灰作用量。

递减还原可得预测值

x(0)(t+1)=(1-ea)[x(0)(1)-u/a]e-a， (t=1，2，…，n).

(6)

2.2 各部门用水数据的模型建立

全数据GM(1，1)模型是由已有时间序列来预测未来数据[10]，未来时间序列越远，则预测的灰值区间越大，同样已有序列随时间的变化越大，预测的数据的精度越低。特别是在的农业、工业和生活用水当中，随着经济水平的不断提升，其时间序列发展的变化非常大。因此针对这种情况，采用越近的短时间序列来进行预测，去掉老旧的数据，同时每预测一步，补充新数据修正灰参数以缩小灰色区间，但要注意预测期，要考虑预测数据的有效性。

GM(1，1)模型是一种单序列模型，将其应用到用水结构时间序列的预测当中，为了减弱数据以外的变量影响，削弱相关性，可将各个用水部门进行单独的预测[11]。

同时考虑到水资源公报数据从2008年正式开始分县级统计，数据较以往统计口径不一致，会给预测结果带来影响，因此，本次预测采用上饶市2008—2018年农业、工业、生活、生态环境的用水量数据，并分别建立GM(1，1)模型。

通过对新数列建立微分方程，并求解，根据最小二乘法原则，利用式(3)～(4)得到4个序列的a和u值，如表2所示。

表2 不同用水部门的a，u值

将a和u值带入GM(1，1)模型，根据式(5)，得到时间相应序列：

对y(1)做递减还原，可以得到x(0)的预测公式：

2.3 模型检验

模型建立好之后，为保证其预测精度需要对模型进行检验，本文GM(1，1)灰色模型采用残差检验和后验差检验[12]。

(1)残差检验

(7)

(2)后验差检验

C=S1/S2，

(8)

其中

(3)模型检验结果

对各部门用水序列做残差和后验差检验，得到结果如表3所示。

根据模型检验精度等级[13]如表4，残差检验中建模精度均>90%既相对误差在0.01以内，为1级，后验差检验中，根据模型精度等级，上饶市生活用水模型为1级，工业和环境用水为2级，农业用水为4级。由于农业需水预测模型精度不够，需要对其进行残差修正。

表3 模型检验结果

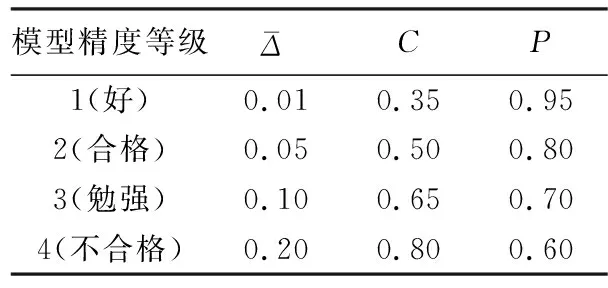
表4 模型精度等级

2.4 GM(1，1)残差模型修正

(9)

2.5 模型预测结果

根据GM(1，1)灰色模型预测各部门的需水情况与真实值对比图显示如图2～3，各个部门的用水量均呈现出逐步增加的趋势。

图2 农业需水预测值、修正后预测值与真实值对比图

图3 工业、生活、生态需水预测值与真实值对比图

农业用水从2018年的22.64亿m3增加到2025年的23.84亿m3；工业用水从2018年的4.10亿m3增加到2025年的5.32亿m3；生活用水从2018年的3.81亿m3增加到2025年的4.78亿m3；生态用水从2018年的0.22亿m3增加到2025年的0.27亿m3。到2019年、2020年、2025年总用水量将分别为32.17，32.65，34.31亿m3。工业用水和生活用水增加比例较为明显，其次是生态用水，增长率最低的是农业用水。

对预测结果进行分析，生活用水和工业用水的增长原因可能是由于经济水平的提高和城市化进程的加快以及工业企业的飞速发展大大的增加了二者的用水消耗，生态环境用水增加主要是由于对绿化环保意识的提高，而农业用水量的缓慢增长一方面是由于许多地方大力发展旅游业，许多农田被改造为景观用地，导致农田灌溉有效面积的减少，二是农业节水措施的不断升级改造和农田高标准建设等使得农田灌溉水系数得到提高，从而减低了农业用水的消耗。

同时根据上饶市水资源管理“三条红线”控制指标，到2020年，2030年用水总量指标的分别为33.7亿m3，34.4亿m3，以及上饶水资源管理中2016—2020年的三条红线各年分解指标，其中2019年的用水总量控制红线为33.5242亿m3。对比预测值可知，2019，2020年的预测值小于三条红线用水总量指标，而2025年的预测值也在2030年的指标值范围内。因此用GM模型来进行预测能较好的反映上饶市未来的用水需求，且年份越近的精度越高，年份越远的就要不断的输入新数据，修正灰色范围，才能使预测值更为合理。

3 结束语

本文基于上饶市2003—2018年的各类用水数据，对上饶市各部门用水进行分析，采用近11 a数据建立了农业、工业、生活及生态需水预测的灰色GM(1，1)模型，通过残差和后验差检验了模型的精度，并对精度较差的农业需水预测模型进行残差修正，得到结论如下：

(1)上饶市的用水结构中以农业用水为主，农业多年平均用水量占总用水量的77.33%，其次为工业用水，年均占总用水量的10.84%，用水量整体呈上涨趋势。

(2)采用残差和后验差检验，根据模型精度等级分级，判定各部门建立的GM(1，1)预测模型中上饶市生活用水模型为1级，工业和环境用水为2级，农业用水为4级。由于农业需水预测模型精度不够，需要对其进行残差修正。

(3)根据GM(1，1)灰色模型预测各部门的需水情况均呈现出逐步增加的趋势。工业用水和生活用水增加比例较为明显，其次是生态用水，农业用水增长率最低。同时预测的总用水量数据均在水资源管理“三条红线”用水总量控制的指标内，预测的数据亦能较好的体现未来近期的一个需水状况，且年份越近的精度越高。