大清河流域气象干旱时空演化和联合概率分析

许怡然 鲁帆 戴雁宇

摘 要：为了评估大清河流域整体气象干旱状况，采用该流域1961—2015年逐日气象数据，基于CI干旱指数和面积阈值法识别区域气象干旱事件，提取历时、干旱面积等指标，分析研究区域气象干旱时空变化特征，并基于Copula函数进行多维干旱特征变量的联合概率分析和重现期计算。结果表明：研究区各地干旱频率相差不大;区域气象干旱程度总体有减轻趋势;冬旱发生的频数最多，春旱多于秋旱，跨季节连旱（尤其是冬春连旱和春夏连旱）较为常见;三维干旱特征变量联合概率能够全面地反映干旱极限特征，在工程设计、水资源决策中安全性更高。

关键词：区域气象干旱;Archimedean Copula函数;联合概率分析;大清河流域

Abstract：In order to study the characteristics of meteorological drought in the Daqing River basin， this study identified regional meteorological drought events based on daily weather data from 1961 to 2015. Copula function was employed to analyze the joint probability of drought duration， area and strength and compute two kinds of return periods. The results indicate that： no significant difference exists in the drought frequency across the study area; the drought strength relieves in the research period; compared with spring and autumn droughts， winter droughts occur most frequently; cross-seasonal droughts， especially winter-to-spring and spring-to-summer droughts are more common. Joint probability analysis of three-dimensional drought characteristic variables can fully reflect the characteristics of extreme drought.

Key words： regional meteorological drought; Archimedean Copula Function; joint probability analysis， Daqing River basin

干旱作為一种频繁发生且极具破坏力的自然灾害之一，发生在全球范围内绝大多数地区，深刻影响当地的生态与社会环境。随着经济社会的高速发展以及人口的快速增长，水资源短缺日益严重，在全球气候变暖的背景下，更突出了干旱问题的严重性。研究干旱的时空分布规律以及干旱风险评价，对于了解、监测干旱发生，提升抗旱减灾能力，保障经济社会、自然生态安全均有重要意义[1-2]。

干旱事件是包括干旱历时、干旱累计缺水量、干旱程度和影响面积等多变量的极值事件，其特征变量之间存在一定的相依关系，仅仅针对单个变量的频率分析方法不足以描述其概率性质，无法全面反映干旱的真实状况。而多变量干旱频率分析则是同时考虑多个干旱指标，通过联合分布来描述干旱的概率，可以更加全面合理地描述干旱随机性。用于多变量水文事件频率的计算方法主要有正态变换法[3-4]、特定边缘分布构成的联合分布[5-6]、非参数方法[7-8]以及工程实践中常用的经验频率法[9]等，上述方法均存在其特定的适用范围和局限性[10]，因此构造相对灵活的Copula函数被广泛应用于多变量水文分析计算领域。1959年Sklar[11]提出Copula理论，将一个联合分布分解为数个边缘分布和用于描述变量之间相关性的一个Copula函数，从而可以构造灵活有效的多元分布，求解相对简单。近些年国内外均有将二维或者三维Copula函数引入干旱频率分析的研究，如Wong等[12]分析了欧洲不同气候区的干旱特征数据并基于二元Copula函数研究了气象和水文干旱之间的关系;肖名忠等[13]采用三变量Plackett Copula函数对干旱历时、严重程度和最小流量3个水文干旱特征变量进行多变量概率分析;马建琴等[14]选取4种对称Archimedean Copula 函数和对应的非对称Archimedean Copula 函数拟合干旱历时、烈度及烈度峰值的三维联合分布并计算联合重现期和同现重现期。但是以往研究很少考虑干旱的区域性，以及干旱事件在持续期中影响范围的动态变化。因此，本文以大清河为例，将区域干旱识别方法和Copula函数结合起来，重点引入影响面积变量，结合干旱历时和干旱强度两个变量，全面评估研究区气象干旱的时空变化，并分析区域气象干旱的3变量联合概率及重现期，以期为大清河流域水利工程规划设计和风险评估提供参考。

1 研究区概况与数据来源

大清河流域地处海河流域中部，西起太行山区，东至渤海湾，北界永定河，南临子牙河，面积为45 131 km2。大清河是海河水系五大河流之一，上游分为南、北两支，均源于太行山，东汇海河入渤海。流域处于温带季风区，多年平均降水量600 mm，降水量年际变化大、年内分配不均，降水多以暴雨形式集中于7—8月，故经常出现连年干旱或先旱后涝、旱涝交替等情况。

本文采用国家气象中心提供的陆面日值气象格点数据，包括降水、相对湿度、气温（距地面2 m处，包括日平均值、最高值、最低值）、风速（距地面10 m处），时间范围为1961年1月1日至2015年12月31日，空间范围为东经113.25°—117.75°、北纬38.25°—39.75°，共36个数据点。日照时间数据来源于中国气象科学数据共享服务网（http：//cdc.nmic.cn），包括全国839个气象站同期观测数据。

2 研究方法

基于大清河流域1961—2015年格点气象数据，采用综合气象干旱指数CI[15]划分单点气象干旱等级，再设定干旱面积阈值，以划分研究区的气象干旱等级，提取区域干旱的频数、起止时间、单日影响面积、累计影响面积、单日干旱强度、累计干旱强度等干旱特征要素，在此基础上统计分析研究区干旱特征，并采用Copula函数分析其联合概率。

2.1 区域气象干旱识别方法

基于前人在区域气象干旱方面的研究成果[16-17]，选择面积阈值法作为区域气象干旱识别方法。统计每天研究区的干旱面积（即干旱的格点数）与研究区总面积的比值A（t），并设定干旱面积阈值At，若A（t）≥At，则认为该天研究区为气象干旱状态。需要说明的是，这种方法可能会识别出多次区域气象干旱过程，其间隔期较短（甚至仅相隔1～2 d），为避免这种情况，需在识别之后再次筛选出间隔期较短的干旱过程（间隔期小于15 d），并将二者合并，合并之后的干旱历时为二者历时之和，累计干旱强度、累计干旱影响面积亦为二者之和。

本文所涉及的干旱特征要素有：干旱历时（干旱开始至干旱结束的总天数）、累计干旱影响面积（干旱期间每天的影响面积之和，本研究区共36个格点，每个格点的面积约为3 025 km2，可简化为采用格点数表示影响面积）、累计干旱强度（干旱期间各天各格点干旱强度之和，即CI值之和，其值越小干旱强度越大）。若某次干旱过程由两个或两个以上短间隔的干旱过程合并而成，则各特征要素为原过程特征要素之和，不包括合并其中的间隔期。干旱面积阈值At不宜过大，否则会遗漏影响面积较小的干旱事件，但也不宜过小，否则起不到“门槛”的作用。为了尽可能真实地反映实际干旱过程，需要进行多次试验比较，并结合当地历史记录来确定干旱面积阈值At。

2.2 多变量干旱特征概率方法

3 结果与分析

3.1 干旱过程识别

在完成所有格点CI值计算的基础上，首先进行干旱面积阈值的试验比对，选定5%、15%、30%、50%、70%和85%等5个试验值，本研究数据实际涉及36个格点，以格点数表示所占面积，分别进行区域气象干旱识别，识别出的区域干旱频数见图1。由图1可知，当干旱面积阈值变化时，四个季度干旱的频数并没有发生明显变化，且大致相等，均在60次左右;而干旱总频数在5%～70%区间内呈上升趋势，在高于70%时呈下降趋势。原因是当干旱阈值较小时，实质上是降低了“门槛”，使得区域干旱的总天数增加，从而使各区域干旱过程合并成具有较长历时的干旱过程，因此区域干旱过程的总频数较少;当“门槛”很高（如85%以上）时，影响面积较小的干旱事件会被排除，从而影响总体的区域干旱过程频数。因此，为真实反映研究区的区域干旱情况，结合当地干旱历史记录[19]，将阈值设定为50%。

当干旱面积阈值设定为50%时，1961—2015年研究区内共发生气象干旱过程126次。提取各干旱过程的干旱历时D、累计干旱影响面积A和累计干旱强度S，将各干旱过程按时间先后顺序编号，绘制成三变量散点图，见图2。可以看出，多数干旱过程集中在D<150 d、A<4 000点、S>-7 000这一范围内（图中左上角部分）;图2右下角的干旱过程则为历时长、范围大、强度高的极端干旱事件，前5位分别为序号87、30、13、7和81的干旱过程，其发生年份分别为2001—2002年、1975—1976年、1967—1968年、1965—1966年和1998—1999年，这与该地区历史上发生重大旱灾的年份大体一致[17]。

3.2 区域气象干旱的时空变化特征

图3为研究期内各站点发生气象干旱的频率，可以看出，研究区各格点在研究期内发生干旱的频率相差不大，均为40%～50%，研究区中部（淀西平原）的干旱频率稍高（50%左右），说明研究区全境均有较大可能发生气象干旱，在空间上的发生频率相差不大。

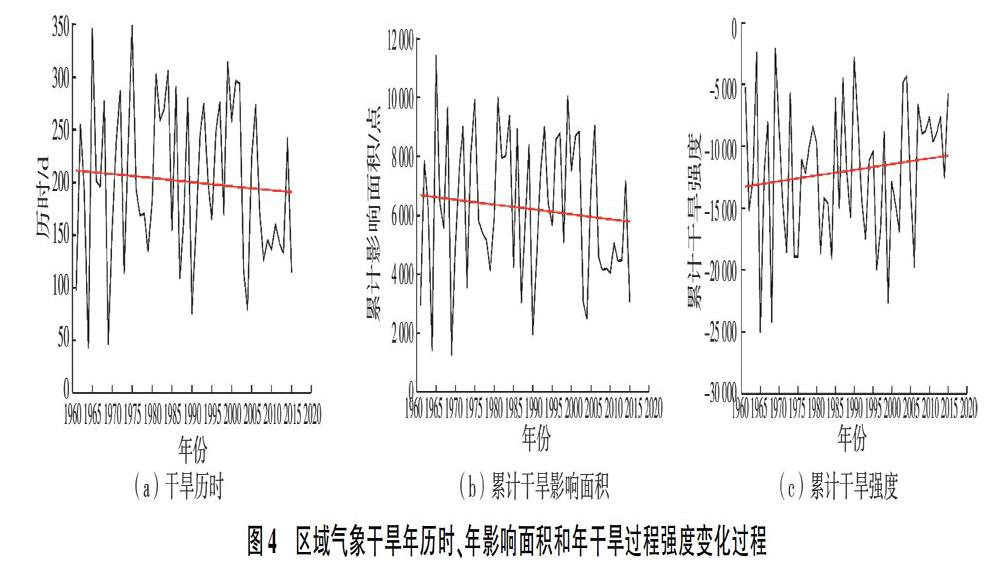
由识别出的126次区域气象干旱过程可知，研究区在研究期内几乎每年都有区域气象干旱。为进一步分析其时间变化特征，统计研究期内每年发生区域气象干旱的历时（每年发生区域气象干旱的天数，值越大即干旱时间越长）、累计影响面积（全年累计的区域气象干旱影响面积，用格点数表示，值越大即干旱的范围越大）以及累计干旱强度（全年累计的区域气象干旱强度，以异常格点的CI值之和表示，值越小即干旱强度越大），见图4（图中红线为趋势线）。由图4可知，1961—2015年研究区气象干旱的历时、累计影响面积均呈下降趋势，而累计干旱强度呈上升趋势。

本文统计了126次区域气象干旱过程的季节干旱情况以及跨季节连旱情况，需要说明的是，若某次干旱过程是连旱，统计季節干旱频数时则会重复统计所涉及的季节，且统计跨季节连旱时，2季连旱事件和3季以上的连旱事件会有重叠，结果见表1。对于各季节的干旱情况，统计结果为：春旱56次、夏旱58次、秋旱47次、冬旱65次。冬旱发生的频数最多，春旱多于秋旱，这与文献[17]结果较为一致。对于跨季节连旱，在126次区域气象干旱事件中，有69次为连旱事件，其中冬春连旱和春夏连旱最为常见，而夏秋连旱出现的频次较低，原因是研究区降水主要集中在7—8两个月，使得盛夏季节成为干旱最轻的季节[17]。研究期内也出现过多次3季及以上的长时间连旱事件，4季连旱出现8次，分别在1962—1963年、1965—1966年、1967—1968年、1980—1981年、1993年、1995—1996年、1998—1999年、2006—2007年，以上年份里研究区均发生较为严重的干旱。

3.3 基于历时-面积-强度的联合干旱频率分析

根据识别的126场区域气象干旱过程的历时（D）、累计干旱强度（S）和累计影响面积（A），拟合干旱特征变量的联合分布并计算相应的重现期。变量之间具有相关性是Copula频率分析的基础，采用Kendall秩相关系数和Spearman秩相关系数，分别对区域气象干旱过程的历时、累计干旱强度和累计影响面积进行两两相关性度量，结果见表2。由表2可知，变量之间均存在很强的相关性，因此运用Copula函数建立变量之间的联合概率分布函数具有可行性。

选取水文频率分析中常用的4种候选边缘分布指数分布（Exponential）、伽马分布（Gamma）、威布尔分布（Weibull）、广义帕累托分布（Generalized Pareto Distribution， GPD），分别拟合历时、影响面积和强度3个干旱特征变量。单变量边缘分布参数估计以及拟合度K-S检验结果见表3。拟合度检验结果表明，干旱历时服从广义帕累托分布、干旱影响面积服从指数分布、干旱强度服从伽马分布，均通过显著性水平为0.05的K-S检验。

选取Clayton Copula、Gumbel Copula、Frank Copula构建二维和三维联合分布函数，采用极大似然法进行Copula函数的参数估计。赤池信息准则（AIC）是衡量统计模型拟合优良性的一种标准，其值越小则模型拟合最优。根据AIC评价Copula函数拟合的优劣性，结果见表4。由表4可知，Frank Copula函数对于D—A、D—S、A—S二维组合以及D—A—S三维组合均具有很好的拟合效果。

根据上文所确定的Frank Copula函数进行二维和三维条件的干旱特征变量联合概率和条件概率分析，并计算相应的重现期，以评估研究区干旱风险。首先统计各干旱特征变量变化范围，发现区域干旱历时、影响面积和干旱强度绝对值的最大值分别为441 d、13 397点、24 769.6，故分别取干旱历时范围为5～500 d，步长5 d;影响面积范围为150～15 000点，步长150点;干旱强度绝对值范围为250～25 000，步长为250。均取100个值，代入各组合对应的Copula函数中，根据式（1）～式（3）确定相应的重现期，见图5～图7。可知，联合重现期的增幅远大于相应的或现重现期，如D=150、A=4 100时，或现重现期略小于5 a，联合重现期则略大于5 a;当D=450、A=12 000时，或现重现期约为100 a，而联合重现期则为500 a。D—|S|和A—|S|组合也有同样的现象。根据重现期曲线可以查阅二维不同组合条件下的重现期。

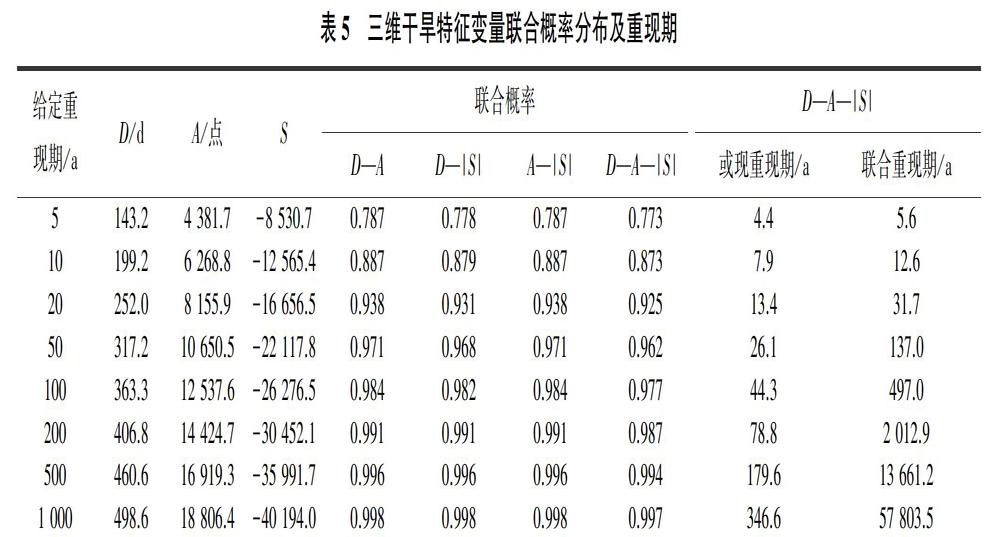
由于用三维干旱变量的Copula联合重现期不易绘制曲面图，因此把一系列给定单变量重现期所对应的边缘分布变量值，代入Copula函数中计算相应的联合概率分布及重现期，结果见表5。与二维联合概率分布情况类似，三维时的或现重现期增长幅度小于联合重现期的，且给定重現期在或现重现期和联合重现期之间，因此在实际工作中可以将或现重现期和联合重现期分别作为单变量重现期的上下限。但是由于联合重现期的条件较为苛刻，当给定单变量重现期为200 a时，对应的联合重现期大于2 000 a，在实际工作中意义不是很大，因此应关注100 a以下的单变量重现期，此时历时、累计影响面积、累计干旱强度分别为363.3 d、12 537.6点、-26 276.5，对应的联合重现期约为500 a，在实际防洪抗旱工作中实用价值更高。

总的来说，二维干旱特征变量联合概率分析关注某两个干旱特征变量组合的影响，虽不够全面，但对于水资源决策者仍有一定的参考价值;三维干旱特征变量联合概率能够更为全面地反映干旱极限特征，其联合重现期比二维重现期大很多，在工程设计、水资源决策中安全性更高，但存在过高重现期不实用的问题，因此在实际工作中可以根据需要选择合适的方法。

4 结 语

（1）大清河流域研究期内共识别出126次气象干旱过程，提取了每一次干旱过程的起止时间以及持续时间内的逐日影响面积和干旱强度，与实际干旱历史记录较为一致。

（2）研究区各地干旱频率相差不大，中部（淀西平原）的干旱频率稍高，为50%左右。区域气象干旱总体来说有减轻的趋势，冬旱发生的频数最多，春旱多于秋旱，跨季节连旱尤其是冬春连旱和春夏连旱较为常见。

本文着眼于研究区的整体干旱情况，相比传统单站研究方法增加了影响面积这一干旱指标，能够全面准确衡量干旱特征，同时采用Archimedean Copula函数族对干旱特征变量进行二维及三维联合频率分析和重现期计算，计算所得的组合重现期可为当地实际抗旱工作提供参考。

参考文献：

[1] 陈玉琼，安顺清，曲建和.近500年京津冀地区最严重的干旱和社会对干旱的响应[J].灾害学，1991（4）：53-57，84.

[2] 李鹏飞， 刘文军， 赵昕奕. 京津冀地区近50年气温、降水与潜在蒸散量变化分析[J]. 干旱区资源与环境， 2015， 29（3）：137-143.

[3] SACKL B， BERGMANN H. ABivariate Flood Model and Its Application[C]//Singh V P. Hydrologic Frequency Modeling. Dordrecht：Springer，1987：571-582.

[4] YUE Sheng. Joint Probability Distribution of Annual Maximum Storm Peaks and Amounts as Represented by Daily Rainfalls[J]. International Association of Scientific Hydrology Bulletin， 2000， 45（2）：315-326.

[5] 谢敏，江志红，丁裕国.运用Gumbel-Logistic模式模拟区域暴雨的试验[J].沙漠与绿洲气象，2011，5（1）：1-5.

[6] YUE Sheng. The Gumbel Logistic Model for Representing a Multivariate Storm Event[J]. Advances in Water Resources， 2001， 24（2）：179-185.

[7] 王文圣，丁晶.基于核估计的多变量非参数随机模型初步研究[J]. 水利学报，2003，34（2）：11-16.

[8] JIN Z， SHAO Y. On Kernel Estimation of a Multivariate Distribution Function[J]. Statistics & Probability Letters， 1999，41：163-168.

[9] 郑红星，刘昌明.南水北调东中两线不同水文区降水丰枯遭遇性分析[J]. 地理学报， 2000， 55（5）： 523-532.

[10] 郭生練，闫宝伟，肖义，等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文，2008，28（3）：1-7.

[11] SKLAR M.Fonctions de RépartitionN Dimensions Et Leurs Marges [J]. Publications de l'Institut de Statistique de l'Université de Paris， 1959， 8：229-231.

[12] WONG G， LANEN H A J V， TORFS P J J F. Probabilistic Analysis of Hydrological Drought Characteristics Using Meteorological Drought[J]. International Association of Scientific Hydrology Bulletin，2013，58（2）：253-270.

[13] 肖名忠，张强，陈永勤，等.基于三变量Copula函数的东江流域水文干旱频率分析[J].自然灾害学报，2013，22（2）：99-108.

[14] 马建琴，和鹏飞，彭高辉，等.基于三维Copula函数的沙颍河流域水文干旱频率分析[J]. 灌溉排水学报， 2017，36（9）：102-107.

[15] 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.气象干旱等级：GB/T 20481—2006[S]. 北京：中国标准出版社，2006：5-6.

[16] REN F， CUI D， GONG Z， et al. An Objective Identification Technique for Regional Extreme Events[J]. Journal of Climate， 2012，25（20）：7015-7027.

[17] 许凯. 我国干旱变化规律及典型引黄灌区干旱预报方法研究[D].北京：清华大学，2015：23-27.

[18] 李计，李毅，宋松柏，等.基于Copulas函数的多维干旱变量联合分布[J].自然资源学报，2013，28（2）：312-320.

[19] 温克刚. 中国气象灾害大典（河北卷）[M]. 北京：气象出版社， 2005：57-75.

【责任编辑 张华兴】