基于BP神经网络的新安江模型初始土壤蓄水量计算研究
2021-03-27张晓斌李抗彬郝改瑞张小鹏
张晓斌,李抗彬,郝改瑞,张小鹏
基于BP神经网络的新安江模型初始土壤蓄水量计算研究
张晓斌1,李抗彬2*,郝改瑞3,张小鹏1
(1.运城学院,山西 运城 044000;2.西安兰特水电测控技术有限责任公司,西安 710043;3.西安理工大学,西安 710048)
【】克服传统经验折减系数法在计算新安江模型初始土壤蓄水量方面的缺点,并提高新安江模型在湿润半湿润地区的应用效果。结合流域初始土壤蓄水量的影响因素和神经网络模型特点,提出构建基于BP神经网络的新安江模型初始土壤蓄水量计算方法。在3种输入因子组合方式下,当BP神经网络隐含层节点大于11时,模拟训练期模型应用效果达到项目精度评价指标的甲等水平,预测检验期的9个样本,均有6个以上样本检验合格;当BP神经网络隐含层节点数从4个变化到21个时,模型评价指标纳什效率系数从0.51变到0.97、均方根误差从11.77降到2.74;与采用传统经验折减系数法计算新安江模型初始土壤蓄水量相比,采用BP神经网络模型应用效果明显占优,且能克服经验折减系数法计算土壤初始蓄水量需要选择流域一场暴雨或久旱未雨才能开始计算和计算过程数据不能中断的缺点。在湿润半湿润地区采用BP神经网络模型计算新安江模型初始土壤蓄水量具有可行性和适用性;当神经网络输入因子和隐含层节点数选择合理时,模型模拟和预测精度较高。
初始土壤蓄水量;BP神经网络;新安江模型;径流模拟
0 引言
随着全球气候变化剧烈活动,洪水灾害频繁发生[1]。针对降水引起的洪水过程,全球水文学者提出不同的水文模型进行流域的降水径流过程模拟预报。刘金涛等[2]指出水文过程模拟除水文模型本身外,模型输入的数据质量是影响模拟精度的关键因素。根据流域降雨形成径流过程的驱动因素分析可知,影响流域降雨径流过程的因素主要包括:气候变化因素、流域土壤类型、植被覆盖度、地形和地貌等[3]。如果水文模型在流域降雨径流过程模拟中输入的这些影响因素数据具有足够精确度,那么模型对水文过程模拟通常会有比较好的精度[4-6]。【研究意义】对于在我国湿润半湿润地区应用比较广泛和成功的新安江模型来说,模型应用过程中存在相同的问题。在模型参数和流域降雨量数据确定情况下,初始土壤蓄水量是影响新安江模型精度的最重要因素,而初始土壤需水量是为反映降雨前流域干旱程度而提出的概念性状态量,并非真实的土壤含水率,因而无法通过测量获得,但其影响因素与流域土壤含水率基本相同[2]。因此通过合理有效的方法对新安江模型初始土壤蓄水量进行确定,对新安江模型应用和提高模拟精度具有重要的意义。【研究进展】目前新安江模型应用过程中,流域初始土壤蓄水量主要采用新安江模型预热法或采用经验折减系数法进行赋值,其他计算方法较少。但这2种方法均存在一定的局限性,如:新安江模型预热法需要较长的预热期;经验折减系数法计算时首先要选择流域中一场大雨或久旱未雨之后才能开始计算,且计算过程数据不能中断。而针对流域真实土壤含水率预测计算方法较多,根据许秀英等[7]统计,主要方法包括:经验法、水量平衡法、时间序列法、神经网络法、遥感监测法等,不同的方法在进行土壤含水率预测计算时各有优缺点。任罡[8]在汾河灌区土壤墒情预报研究中指出,经验法建模公式简单,但精度较低,系数易受数据时空分布影响;侯琼等[9]在对内蒙古典型草原土壤水分动态研究中表明,水量平衡法计算简单,但所需测量和计算因素较多,预测精度受各分量测定方法和技术影响明显;白冬妹等[10]采用时间序列法进行对黄土丘陵半干旱区柠条林地的土壤含水率进行预测,结果表明时间序列法在短期内预测效果良好,但在中长期土壤水分预测时有一定的局限性;郭庆春等[11]采用神经网络模型建立驻马店地区深层土壤含水率预测模型,结果表明预测模型精度较高,但模型输入因子对预测精度有影响;刘影等[12]在土壤含水率高光谱遥感定量反演研究进展中指出遥感监测法需要积累大量的观测数据、工作量大,模型不稳定,适用于大范围土壤水分预测,预测精度受地面实测资料的多少和分布影响较大。【切入点】综上所述,以往的研究多集中在流域真实土壤含水率预测方法上,而针对新安江模型初始土壤蓄水量计算方法研究较少,且已有的方法存在一定的局限性。【拟解决的关键问题】因此本文结合流域真实土壤含水率预测计算方法的特点,以及新安江模型初始土壤蓄水量的影响因素,提出基于BP神经网络的新安江模型初始土壤蓄水量计算方法,期望为新安江模型在湿润半湿润地区应用过程中初始土壤蓄水量计算提供新的参考方法。
1 材料与方法
1.1 研究流域概况
石头河水库位于陕西省宝鸡市眉县,水库坝址以上控制流域面积为673 km2。流域属于暖温带半湿润大陆性气候,植被覆盖度高,流域降水主要集中在7—9月,多年平均降水量在816 mm以上,多年平均气温在12 ℃左右[13]。
1.2 方法介绍
1.2.1 BP神经网络
神经网络是由神经元之间通过相互连接而组成[14-15],通常神经网络结构是由输入层、隐含层和输出层组成。在神经网络应用中,BP神经网络最常用,其是一种多层前馈型网络[16-17],其算法核心思想为梯度下降法,是在误差传递过程中采用梯度搜索技术,以使网络的实际输出值和期望输出值之间的误差平方和为最小[18-19]。BP神经网络算法具体原理可参见文献[20]。
1.2.2 新安江模型
新安江模型是赵人俊[21]提出的一种集总式概念性模型,主要适用于湿润半湿润地区的降雨径流过程模拟预报。模型以蓄满产流理论为主,指出在流域中包气带土壤含水率在没有达到土壤田间持水率之前,流域的降水将全部被土壤吸收用来补充土壤含水率,不会形成产流;当流域包气带土壤含水率达到田间持水率时,降水将全部形成产流[22]。新安江模型详细介绍参见文献[23]。
1.2.3 经验折减系数法[23]
在新安江模型进行场次洪水计算时,降雨起始时间对应的初始土壤蓄水量通常采用前期影响雨量代替。前期影响雨量常采用经验折减系数法进行计算,计算式为:
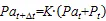
式中:Pa为时刻前期影响雨量(mm);P为时段内降雨量(mm);为土壤含水率折减系数;Pa△为+Δ时刻前期影响雨量(mm)。
1.3 基于BP神经网络的新安江模型初始土壤蓄水量计算模型构建
新安江模型在流域降雨径流过程模拟预报中,模型输入的降雨开始前流域初始土壤蓄水量受多种因素影响[24],这些因素之间相互作用,构成流域内复杂的非线性水循环系统。对于这种复杂的非线性系统模拟,神经网络方法具有很强的优势,因此,可采用BP神经网络构建计算新安江模型初始土壤蓄水量的方法。
1.3.1 模型输入和输出的确定
在影响流域初始土壤蓄水量众多因素中,流域地形、土壤类型随时间变化较小,而流域植被覆盖度和气候影响因素均随时间实时发生变化,因此构建基于BP神经网络初始土壤蓄水量计算模型时,可将反映流域植被覆盖度和气候变化的因素作为模型的输入因子[25-26]。由文献[2]可知,在流域次洪模拟过程中,流域初始土壤蓄水量与流域降水前的15~22 d内气候变化关系最为密切,因此模型输入因子可采用洪水场次降雨开始前的15~22 d内的数据统计获得。
1.3.2 隐含层节点数的确定
隐含层节点数过多或过少不仅关系神经网络性能好坏,同时也影响神经网络结构的复杂度,但目前神经网络模型隐含层节点数确定并无较好办法或统一的计算规则[27-28],只能根据经验确定BP神经网络模型隐含层节点数变化范围在/2~21之间(其中为输入层因子个数),然后通过试算选择合理的网络隐含层节点数。
1.3.3 激活函数的确定
神经元激活函数主要是用来提高神经网络结构的非线性表达能力。最常见的是将S型函数和线性函数相互组合,这样既能兼顾神经网络的非线性映射能力,又可以提高神经网络的计算性能[29]。
1.3.4 权重、阈值调整
BP神经网络在网络权重和阈值调整过程中,采用不同的训练函数会影响网络的计算耗时和收敛速度。网络训练时选择哪一个训练函数并无统一要求,因此可根据具体情况选择合适的训练函数[30-31]。
1.4 BP神经网络初始土壤蓄水量计算方法与新安江模型耦合
通过对降雨前流域初始土壤蓄水量影响因素统计,构建基于BP神经网络的新安江模型初始土壤蓄水量计算方法,然后将计算的初始土壤蓄水量作为新安江模型的输入量代入到新安江模型中,可将基于BP神经网络的新安江模型初始土壤蓄水量计算方法与新安江模型耦合起来,用于流域的洪水过程降雨径流过程模拟和预报。
1.5 研究流域数据收集及整理
根据构建的基于BP神经网络的新安江模型初始土壤蓄水量计算模型与新安江模型耦合应用要求,收集研究流域内遥感、水文以及气象数据包括:1998—2018年不同月份流域归一化植被指数()[32]空间分布数据(数据来源于中国科学院资源环境科学数据中心:http://www.resdc.cn)、1991—2018年水库入库流量数据和流域雨量站(高码头、杜家庄、桃川、牛心石)降水量数据以及1991—2018年流域周围气象站(宝鸡县、太白县、眉县)的气象数据。流域各站点分布及流域位置如图1所示。
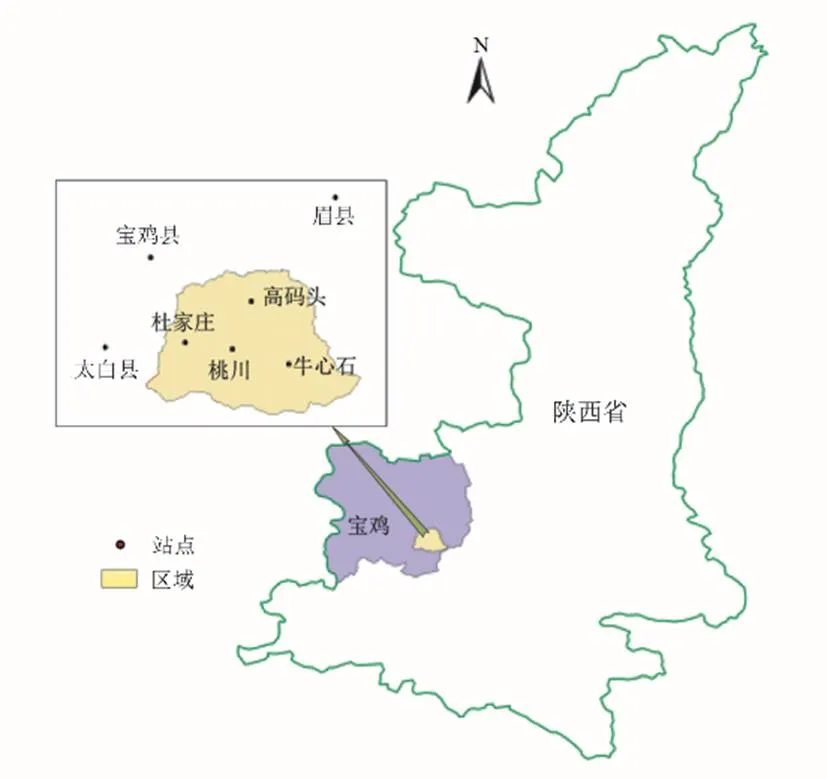
图1 研究流域位置及站点分布
对研究流域收集的数据进行整理和统计,步骤如下:
1)对雨量站数据采用泰森多边形法计算流域面平均雨量数据序列;对气象站数据采用算术平均数法计算流域各气象因子数据序列;根据收集的流域归一化植被指数空间分布数据,统计流域不同年份各月归一化植被指数平均值,并计算流域多年各月归一化植被指数平均值数据序列,然后通过样条插值获得流域年内不同日期多年归一化植被指数平均值数据序列。
2)根据计算的流域面平均雨量及收集的水库入流量数据序列,整理流域的洪水场次数据序列。
3)根据整理的洪水场次数据序列、流域面平均雨量数据序列、流域各气象因子数据序列以及流域多年归一化植被指数平均值数据序列,提取各场洪水降雨起始时间前21天内流域面平均雨量数据序列、流域各气象因子数据序列以及多年平均归一化植被指数平均值数据序列。
4)采用经验折减系数法进行流域新安江模型参数率定,在新安江模型参数确定后反推得到流域各洪水场次降雨起始时间对应的最优初始土壤蓄水量数据(反推计算时,使每一场洪水场次降雨起始时间对应的初始土壤蓄水量在代入新安江模型后计算的径流深与实测径流深误差小于±0.1 mm),将该数据作为建立BP神经网络初始土壤蓄水量计算模型的输出样本。
5)根据提取的流域各洪水场次前21天内面平均雨量数据序列、流域各气象因子数据序列以及多年归一化植被指数平均值数据序列,统计得到建立BP神经网络初始土壤蓄水量计算模型的输入样本。
根据以上步骤,整理统计获得流域年内不同日期多年归一化植被指数平均值数据序列如图2所示;在新安江模型参数确定后,根据各洪水场次实测径流深反推得到各洪水场次降雨起始时间对应的流域初始土壤蓄水量如图3所示。
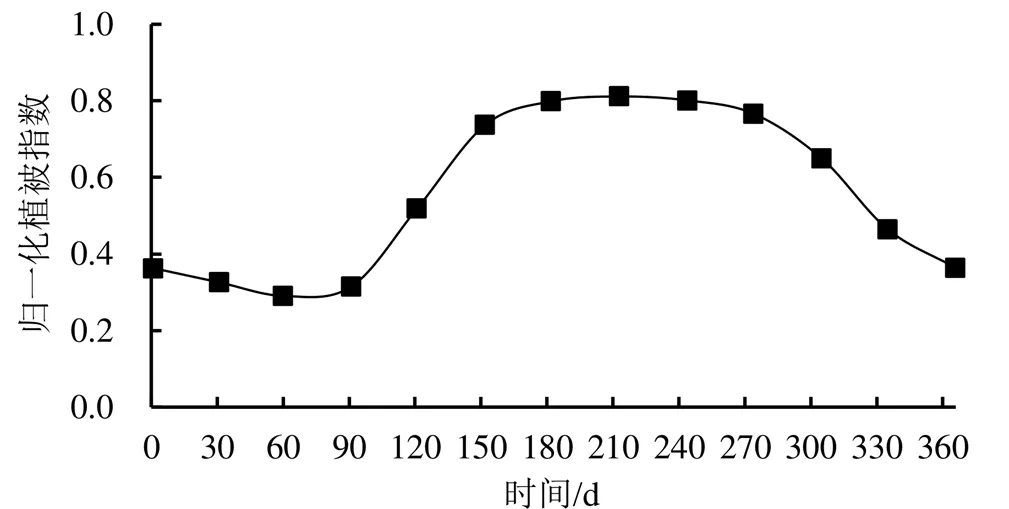
图2 流域年内不同日期多年平均归一化植被指数平均值
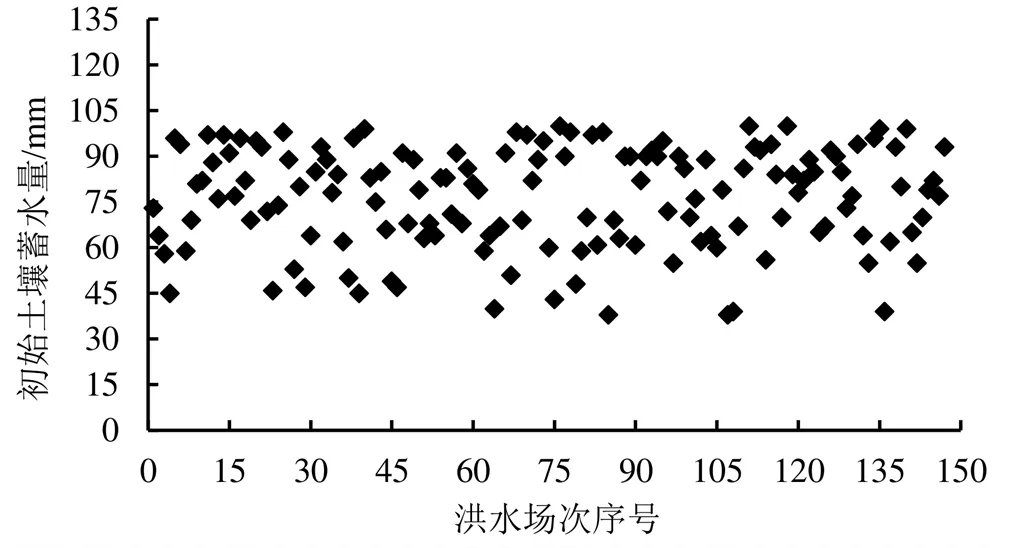
图3 各洪水场次降雨起始时间对应初始土壤蓄水量
由图3可知,研究流域不同洪水场次起始时间对应的初始土壤蓄水量分布在35~100 mm之间,数值比较离散,具有代表性。
对于BP神经网络初始土壤蓄水量计算模型的输入样本,通过流域不同洪水场次起始时间前21天水文气象因素数据序列以及多年日平均数据序列统计得到。由于统计时段划分不同,输入因子的组成也不相同,统计时段划分过小则模型因子较多,统计时段划分过大则模型因子较少,因此在实际应用过程中可根据资料收集情况选择不同的统计时段进行因子统计。本文采用以下3种因子组合方式进行输入样本统计,第一种:降雨前第1~3、第4~6、第7~9、第10~12、第13~15、第16~18、第19~21天累积降雨量、降雨前20天平均气温、平均湿度、平均气压、平均日照时间、平均风速、平均;第二种:降雨前第1~4、第5~8、第9~12、第13~16、第17~20天累积降雨量、其他因子(平均湿度、平均气压、平均日照时间、平均风速、平均)统计同第一种;第三种:降雨前第1~5、第6~10、第11~15、第16~20天累积降雨量、其他因子(平均气温、平均湿度、平均气压、平均日照时间、平均风速、平均)统计同第一种。
1.6 方法评价指标
为验证基于BP神经网络的新安江模型初始土壤蓄水量计算方法的效果,选择相对误差、纳什效率系数、均方根误差作为模型应用好坏的评价指标[33]。
相对误差计算式为:
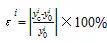
纳什效率系数计算式为:
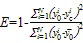
均方根误差计算式为:


2 模型应用结果及对比分析
2.1 模型应用结果分析
采用研究流域147场洪水过程数据、反推获得的流域初始土壤蓄水量数据以及通过统计获得的神经网络3种输入因子组合数据构成基于BP神经网络的新安江模型初始土壤蓄水量计算方法与新安江模型耦合应用的模拟训练期和预测检验样本数据。模型训练期样本数据来自1991—2016年,预测检验期样本数据来自2017—2018年。
采用MATLAB软件编写相应模型程序,并以各洪水场次计算径流深与实测径流深相对误差小于实测径流深的20%作为样本合格的评价指标(实测径流深的20%大于20 mm时,以20 mm为误差允许上限),通过训练计算得到在不同输入因子和隐含层节点下模拟训练期合格样本数和模型评价指标变化过程线图和预测检验期合格样本数变化过程线图,如图4、图5所示。
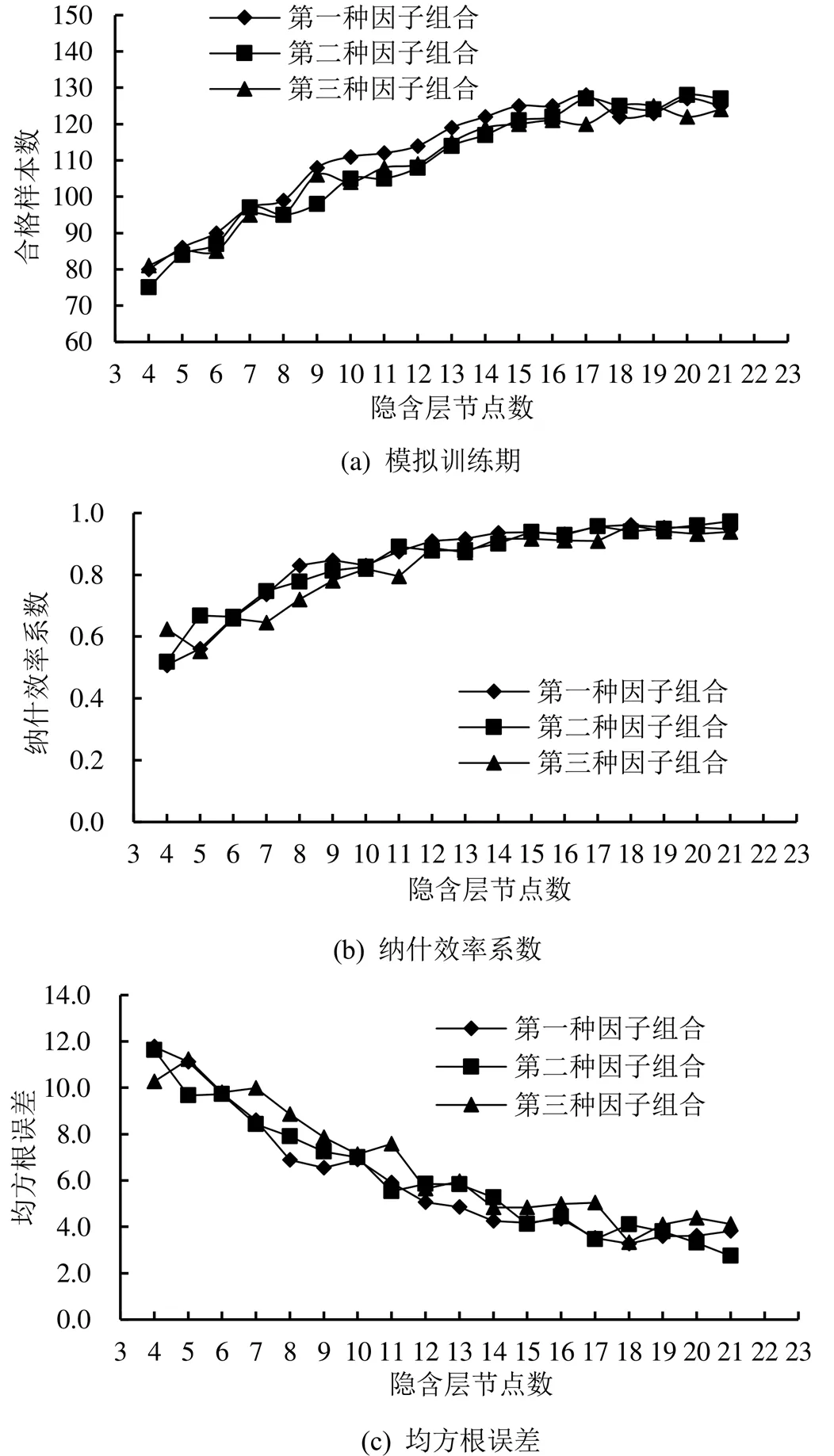
图4 模拟训练期样本合格数及模型评价指标变化过程线
由图4可知,在模拟训练期,基于BP神经网络的新安江模型初始土壤蓄水量计算方法在隐含层节点数小于18时,随着隐含层节点数的增加,不同输入因子下模型耦合应用得到合格样本数呈逐渐增加趋势,当隐含层节点数超过18个以后,训练合格样本数和纳什效率系数增加趋势以及均方根误差下降趋势明显变缓。当隐含层节点数从4个变化到21个,模拟训练样本合格率从54.3%变化到92.8%、纳什效率系数从0.51变到0.97、均方根误差从11.77降到2.74。其中当隐含层节点数大于11时,基于BP神经网络的新安江模型初始土壤蓄水量计算方法与新安江模型耦合应用样本合格率达到水情预报项目精度评价等级的甲等水平,效果良好,表明该方法具有可行性。
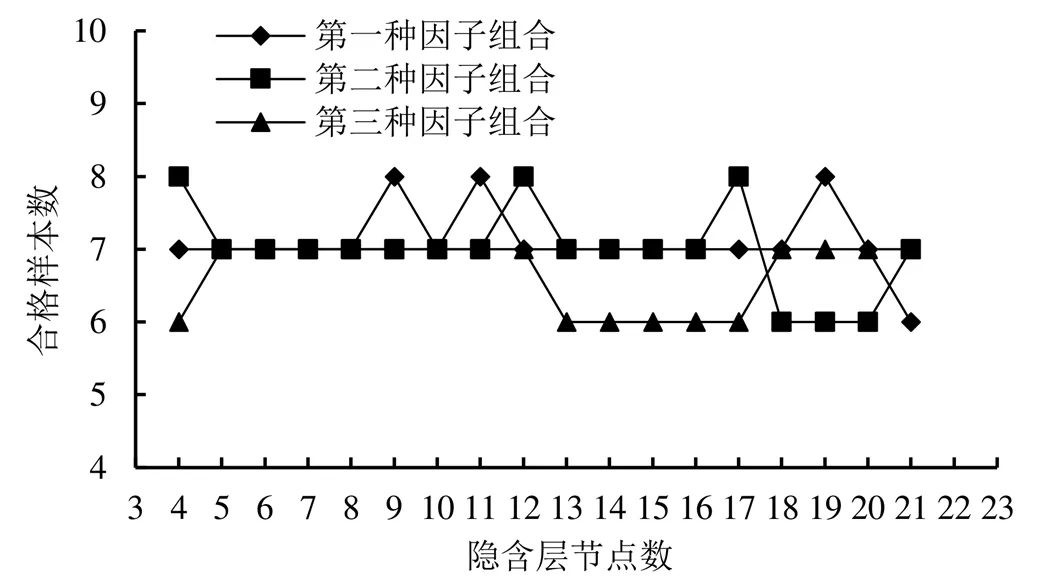
图5 预测检验期样本合格数变化过程线
由图5可知,在预测检验期,不同输入因子和隐含层节点下合格样本数均在6场以上,达到水情预报项目精度评价等级的丙等水平以上。当隐含层节点数小于18时,第一种与第二种因子组合在检验期的样本合格率要好于第三种因子组合,预测效果达到水情预报项目精度评价等级的乙等水平以上。
新安江模型在湿润半湿润地区场次洪水过程模拟预报时,采用基于BP神经网络的新安江模型初始土壤蓄水量计算方法计算洪水场次降雨开始时新安江模型输入的初始土壤蓄水量具有可行性和适用性。
2.2 与经验折减系数法应用结果对比分析
在研究流域,新安江模型参数是通过参数率定获得。在参数率定过程中各洪水场次降雨开始时间对应的初始土壤蓄水量是采用经验折算系数法计算得到,因此模型参数率定过程中目标函数最优所对应的洪水场次合格数即为经验折减系数法计算的模拟期合格样本数。预测检验期合格样本数可通过新安江模型参数带入计算统计获得。通过计算统计,采用经验折减系数法计算新安江模型初始土壤蓄水量,并代入到新安江模型得到模拟期合格样本数为104场,预测检验期合格样本数为5场。与采用BP神经网络的新安江模型初始土壤蓄水量计算方法相比,当BP神经网络隐含层节点数大于11时,3种输入因子组合方式下模拟训练期和预测检验期结果均要优于传统的经验折减系数法。这也表明基于BP神经网络的新安江模型初始土壤蓄水量计算方法具有可行性和适用性。
3 讨论
3.1 基于BP神经网络的新安江模型初始土壤蓄水量计算方法与传统方法计算特点对比
基于BP神经网络的新安江模型初始土壤蓄水量计算方法是通过统计各洪水场次起始时间之前15~22天的水文、气象等要素构建模型输入因子,并采用网络训练构建模型,建模和应用过程相对简单,输入因子和隐含层节点数选择合理时模型的精度较高,与郭庆春等[11]、李兴旺等[34]采用神经网络法进行流域真实土壤含水率预测计算时结论相同;而经验折减系数法首先需要根据流域气象资料确定经验折减系数,其次,需要选择起算值(通常为久旱之后或暴雨之后),最后在起算值确定后连续往后计算[35];新安江模型预热法通过模型连续计算来调整初始土壤蓄水量,计算过程由于初始土壤蓄水量初值误差较大,会导致开始计算的前几场洪水过程计算值与实测值误差较大,因此需要较长的预热期才能应用。由3种方法的计算特点可知,经验折减系数法和新安江模型预热法由于需要连续计算,所以对数据的连续性要求要高于基于BP神经网络的新安江模型初始土壤蓄水量计算方法。
3.2 基于BP神经网络的新安江模型初始土壤蓄水量计算方法不足和未来研究方向
通过验证可知,基于BP神经网络的新安江模型初始土壤蓄水量计算方法在湿润半湿润地区具有可行性和适用性,但是由于建模过程是通过网络训练完成的,因此模型训练样本数据的好坏和模型输入因子的合理性会影响模型应用效果。文中虽然通过3种因子组合方式构建了基于BP神经网络的新安江模型初始土壤蓄水量计算法,且模拟和预测效果要优于经验折减系数法,但是否还有其他更有效的因子组合方式,需要进一步对比研究。例如:增加流域真实土壤含水率卫星产品、模型模拟产品等作为模型输入因子或删减一些对计算影响较小的模型输入因子等,从而优化BP神经网络的结构,选择更加合理的模型输入因子,达到提高模型的模拟预报精度目标。
4 结论
1)在研究流域新安江模型参数确定情况下,采用基于BP神经网络的新安江模型初始土壤蓄水量计算方法进行洪水场次降雨开始时初始土壤蓄水量计算完全可行,且具有较好的适用性。
2)当BP神经网络隐含层节点数选择合理时,该方法在模拟期和检验期计算结果要明显优于传统经验折减系数法,且能够克服经验折减系数法的缺点。
[1] 曾维华, 程声通. 环境灾害学引论[M]. 北京: 中国环境科学出版社, 2000.
ZENG Weihua, CHENG Shengtong. Introduction to Environmental Disaster Science [M]. Beijing: China Environment Science Press, 2000.
[2] 刘金涛, 张佳宝. 前期土壤含水量对水文模拟不确定性影响分析[J]. 冰川冻土, 2006, 28(4): 519-525.
LIU Jintao, ZHANG Jiabao. Effect of antecedent soil water content on the uncertainty of hydrological simulation[J]. Journal of Glaciology and Geocryology, 2006, 28(4): 519-525.
[3] 徐玉英. 土壤含水量计算方法[J]. 东北水利水电, 2005, 23(7): 29-30.
XU Yuying. Calculation method of soil moisture[J]. Water Resources & Hydropower of Northeast China, 2005, 23(7): 29-30.
[4] 牛宏飞, 张钟莉莉, 孙仕军, 等. 土壤墒情预测模型对比[J]. 中国农业大学学报, 2018, 23(8): 142-150.
NIU Hongfei, ZHANGZHONG Lili, SUN Shijun, et al. Comparative study on soil moisture content prediction model[J]. Journal of China Agricultural University, 2018, 23(8): 142-150.
[5] 仝兆远, 张万昌. 土壤水分遥感监测的研究进展[J]. 水土保持通报, 2007, 27(4): 107-113.
TONG Zhaoyuan, ZHANG Wanchang. Progress of soil moisture monitoring by remote sensing[J]. Bulletin of Soil and Water Conservation, 2007, 27(4): 107-113.
[6] 刁万英, 刘刚, 胡克林. 基于高光谱特征与人工神经网络模型对土壤含水量估算[J]. 光谱学与光谱分析, 2017, 37(3): 841-846.
DIAO Wanying, LIU Gang, HU Kelin. Estimation of soil water content based on hyperspectral features and the ANN model[J]. Spectroscopy and Spectral Analysis, 2017, 37(3): 841-846.
[7] 许秀英, 衣淑娟, 黄操军. 土壤含水量预报现状综述[J]. 农机化研究, 2013, 35(7): 11-15.
XU Xiuying, YI Shujuan, HUANG Caojun. Soil moisture content prediciton situation review[J]. Journal of Agricultural Mechanization Research, 2013, 35(7): 11-15.
[8] 任罡. 汾河灌区土壤墒情预报经验模型[J]. 科技情报开发与经济, 2008, 18(34): 88-90.
REN Gang. The empirical model for the forecast of soil moisture in Fenhe irrigated area[J]. Sci-Tech Information Development & Economy, 2008, 18(34): 88-90.
[9] 侯琼, 王英舜, 杨泽龙, 等. 基于水分平衡原理的内蒙古典型草原土壤水动态模型研究[J]. 干旱地区农业研究, 2011, 29(5): 197-203.
HOU Qiong, WANG Yingshun, YANG Zelong, et al. Establishing soil water dynamic model for typical steppe based on water balance principle[J]. Agricultural Research in the Arid Areas, 2011, 29(5): 197-203.
[10] 白冬妹, 郭满才, 郭忠升, 等. 时间序列自回归模型在土壤水分预测中的应用研究[J]. 中国水土保持, 2014(2): 42-45.
BAI Dongmei, GUO Mancai, GUO Zhongsheng, et al. Application of time series autoregressive model in soil moisture prediction[J]. Soil And Water Conservation In China, 2014(2): 42-45.
[11] 郭庆春, 何振芳. 基于人工神经网络的土壤含水量预报模型[J]. 山西农业科学, 2012, 40(8): 892-895.
GUO Qingchun, HE Zhenfang. Forecast model of soil water content based on artificial neural network[J]. Journal of Shanxi Agricultural Sciences, 2012, 40(8): 892-895.
[12] 刘影, 姚艳敏. 土壤含水量高光谱遥感定量反演研究进展[J]. 中国农学通报, 2016, 32(7): 127-134.
LIU Ying, YAO Yanmin. Research progress of soil moisture quantitative inversion by hyperspectral remote sensing[J]. Chinese Agricultural Science Bulletin, 2016, 32(7): 127-134.
[13] 刘拓. 智慧水库灌区信息系统建设技术研究及应用[D]. 西安: 西安理工大学, 2017.
LIU Tuo. Research and application of information system construction in intelligent reservoir irrigation[D]. Xi’an: Xi’an University of Technology, 2017.
[14] ZENG X Y, SHU L, HUANG G M, et al. Triangular fuzzy series forecasting based on grey model and neural network[J]. Applied Mathematical Modelling, 2016, 40(3): 1 717-1 727.
[15] 罗党, 王浍婷. 灰色神经网络下的多变量土壤含水量预测模型[J]. 华北水利水电大学学报(自然科学版), 2017, 38(5): 70-75.
LUO Dang, WANG Huiting. Prediction model of multivariate soil water content constructed by the grey model combined with neural network and three-parameter interval grey number[J]. Journal of North China University of Water Resources and Electric Power, 2017, 38(5): 70-75.
[16] 赵文刚, 马孝义, 刘晓群, 等. 基于神经网络算法的广东省典型代表站点0简化计算模型研究[J]. 灌溉排水学报, 2019, 38(5): 91-99.
ZHAO Wengang, MA Xiaoyi, LIU Xiaoqun, et al. Using neural network model to simplify0calculation for representative stations in Guangdong Province[J]. Journal of Irrigation and Drainage, 2019, 38(5): 91-99.
[17] RASTEGAR R, HARIRI A. A step forward in studying the compact genetic algorithm[J]. Evolutionary Computation, 2006, 14(3): 277-289.
[18] 江衍铭, 郝偌楠, 李楠楠, 等. 基于静态与动态神经网络的运河水位预报[J]. 天津大学学报, 2017, 50(3): 245-254.
CHIANG Yenming, HAO Ruonan, LI Nannan, et al. Water level forecasting by static and dynamic neural networks[J]. Journal of Tianjin University, 2017, 50(3): 245-254.
[19] 王建金, 石朋, 瞿思敏, 等. 改进BP神经网络算法在中小流域洪水预报中的应用研究[J]. 西安理工大学学报, 2016, 32(4): 475-480.
WANG Jianjin, SHI Peng, QU Simin, et al. Application of improved BP neural network algorithm in flood forecasting in the middle and small watershed[J]. Journal of Xi’an University of Technology, 2016, 32(4): 475-480.
[20] 杨章. 基于降维LBP与叶片形状特征的植物叶片识别方法[D]. 武汉: 湖北工业大学, 2018.
YANG Zhang. Plant leaves recognition method based on dimension reduction local binary pattern and shape features of leaves[D]. Wuhan: Hubei University of Technology, 2018.
[21] 赵人俊. 流域水文模拟--新安江模型与陕北模型[M]. 北京: 水利电力出版社, 1984.
ZHAO Renjun. Watershed hydrological modeling – Xin’anjiang model and northern Shaanxi model[M] Beijing: China Water Power Press, 1984.
[22] 陈琳, 王健, 宋鹏帅, 等. 降雨对坡耕地地表结皮土壤水稳性团聚体变化研究[J]. 灌溉排水学报, 2020, 39(1): 98-105.
CHEN Lin, WANG Jian, SONG Pengshuai, et al. Effect of rainfall on water stability aggregates of crust soil on slope surface[J]. Journal of Irrigation and Drainage, 2020, 39(1): 98-105.
[23] 包为民. 水文预报[M]. 北京: 中国水利水电出版社, 2006.
BAO Weimin. Hydrological Forecast [M]. Beijing: China Water Power Press, 2006.
[24] 刘燕. 气候变化对干旱区资源植物开发模式的影响[D]. 南京: 南京信息工程大学, 2017.
LIU Yan. Impacts of Climate Change on Plant Exploitation Patterns in Arid Areas [D]. Nanjing: Nanjing University of Information Science & Technology, 2017.
[25] 张愉, 吴柏清, 陈辉. 气候因子变化与植被指数关联性研究[J]. 内江科技, 2012 (6): 35-36.
ZHANG Yu, WU Baiqing, CHENG Hui. Study on the relationship between climate factor change and vegetation index [J]. Neijiang Keji, 2012, (6): 35-36.
[26] KIM S E, SEO I W. Artificial neural network ensemble modeling with exploratory factor analysis for streamflow forecasting[J]. Journal of Hydroinformatics, 2015, 17(4): 614-639.
[27] BAHADIR E. Prediction of prospective mathematics teachers’ academic success in entering graduate education by using back-propagation neural network[J]. Journal of Education and Training Studies, 2016, 4(5): 113-122.
[28] 王嵘冰, 徐红艳, 李波, 等. BP神经网络隐含层节点数确定方法研究[J]. 计算机技术与发展, 2018, 28(4): 31-35.
WANG Rongbing, XU Hongyan, LI Bo, et al. Research on method of determining hidden layer nodes in BP neural network[J]. Computer Technology and Development, 2018, 28(4): 31-35.
[29] 崔丽杰. 基于BP神经网络的训练函数选取研究[J]. 科技创新导报, 2014(36): 4, 29.
CUI Lijie. Research on the training function selection based on BP neural network [J]. Science and Technology Innovation Herald, 2014 (36): 4, 29.
[30] 胡健伟, 周玉良, 金菊良. BP神经网络洪水预报模型在洪水预报系统中的应用[J]. 水文, 2015, 35(1): 20-25.
HU Jianwei, ZHOU Yuliang, JIN Juliang. Flood forecasting model on BP neural networks and its application in flood forecasting systems[J]. Journal of China Hydrology, 2015, 35(1): 20-25.
[31] 刘威, 刘尚, 白润才, 等. 互学习神经网络训练方法研究[J]. 计算机学报, 2017, 40(6): 1 291-1 308.
LIU Wei, LIU Shang, BAI RunCai, et al. Research of mutual learning neural network training method[J]. Chinese Journal of Computers, 2017, 40(6): 1 291-1 308.
[32] 程杰, 杨亮彦, 黎雅楠. 2000—2018年陕北地区时空变化及其对水热条件的响应[J]. 灌溉排水学报, 2020, 39(5): 111-119.
CHENG Jie, YANG Liangyan, LI Ya’nan. Spatiotemporal variation inand its response to hydrothermal change from 2000 to 2018 in northern Shaanxi Province[J]. Journal of Irrigation and Drainage, 2020, 39(5): 111-119.
[33] 宋晓猛, 孔凡哲. 新安江模型和人工神经网络的耦合应用[J]. 水土保持通报, 2010, 30(6): 135-138, 144.
SONG Xiaomeng, KONG Fanzhe. Application of xinanjiang model coupling with artificial neural networks[J]. Bulletin of Soil and Water Conservation, 2010, 30(6): 135-138, 144.
[34] 李兴旺, 冯宝平. 基于BP神经网络的土壤含水量预测[J]. 水土保持学报, 2002, 16(5): 117-119.
LI Xingwang, FENG Baoping. Prediction of soil water content based on BP neural network[J]. Journal of Soil and Water Conservation, 2002, 16(5): 117-119.
[35] 叶守泽, 詹道江. 工程水文学[M]. 北京: 中国水利水电出版社, 2000.
YE Shouze, ZHAN Daojiang. Engineering Hydrology[M]. Beijing: China Water Power Press, 2000.
Using BP Network to Estimate Initial Soil Water Storage in Xin’anjiang Model
ZHANG Xiaobin1, LI Kangbin2*, HAO Gairui3, ZHANG Xiaopeng1
(1. Yuncheng University, Yuncheng 044000, China; 2. Xi’an Land Water and Electricity Measurement and Control Co.Ltd, Xi’an 710043, China; 3. Xi’an University of Technology, Xi’an 710048, China)
【】Xin’anjiang model is a hydrological model widely used for catchment modelling, but it application needs to know the initial soil moisture storage. Such initial soil moistures were traditionally estimated using the empirical reduction coefficient method which has some shortcomings, and this paper aims to present an alternative method to improve the estimate of this initial soil moisture storage when applying the model to humid and semi humid areas.【】The proposed method is based on the BP neural network and calculates the initial soil moisture storage using some easy-to-measure factors that are thought to affect moisture distribution in soil.【】Using three input factors, when the number of nodes in the hidden layer was more than 11, the accuracy index of the BP network model reached first-class level during the training stage. Of the nine samples used in the test of the model, six met the required criterion. It was also found that when the number of the nodes in the hidden layer varied between 4 and 21, the Nash–Sutcliffe efficiency coefficient in the model evaluation increased from 0.51 to 0.97, with the associated root mean square errors decreasing from 11.77 to 2.74. Compared with the traditional empirical reduction coefficient method, the BP neural network model is superior in resolving the constraints in the former, including that it needs a rainstorm or a long drought to start the calculation and that the calculation needs to be continuous in time.【】The BP neural network model proposed in this paper is feasible to calculate the initial soil water storage when applying the Xin’anjiang model to humid and semi humid areas. It can accurately estimate the initial soil water storage in a catchment if the number of input factors and the nodes in the hidden layers are rationally selected.
initial soil water storage; BP neural network; Xin’anjiang model; runoff simulation
P338.9
A
10.13522/j.cnki.ggps.2020324
1672 - 3317(2021)03 - 0015 - 08
张晓斌, 李抗彬, 郝改瑞, 等. 基于BP神经网络的新安江模型初始土壤蓄水量计算研究[J]. 灌溉排水学报, 2021, 40(3): 15-22.
ZHANG Xiaobin, LI Kangbin, HAO Gairui, et al. Using BP Network to Estimate Initial Soil Water Storage in Xin’anjiang Model[J]. Journal of Irrigation and Drainage, 2021, 40(3): 15-22.
2020-06-16
国家自然科学基金项目(51479215);山西省水利厅科技项目(TZ2019026);运城学院博士科研项目(YQ-2020003)
张晓斌(1977-),男,山西临猗人。教授,主要从事流域水资源水环境模拟及污染控制研究。E-mail: 277723402@qq.com
李抗彬(1981-),男,陕西韩城人。高级工程师,主要从事流域水文水资源模拟及水利信息化研究。E-mail: winer891@sina.com
责任编辑:白芳芳
