基于山脊地形台风风场的铁塔风振系数研究

赵云龙 翁兰溪 黄文超 黄宴委

（1. 福州大学电气工程与自动化学院，福州 350108；2. 福建省电力勘测设计院，福州 350003）

0 引言

我国超特高压输电线路急速发展，为社会经济运行提供了基础能源保障。但是输电线路倒塔断线事故每年时有发生，造成了重大经济损失，特别是在台风多发的东南沿海区域。因此，提高输电线路铁塔的抗风能力是非常重要的课题。近年来，很多学者对输电铁塔在良态风场下的风振响应特性进行了研究[1-3]。杨挺等进行了输电铁塔分段全尺寸模型的风洞试验，研究了分段铁塔模型的竖向风荷载在中低风速下随风速变化规律[4]。赵建等针对长悬臂输电铁塔，通过数值模拟得到不同高度层风荷载并施加到铁塔模型上，计算得到塔身和横担处的风振系数，并进行了安全性验证，能够满足实际工程需要[5]。在良态风场输电铁塔风振响应研究基础上，国内外诸多学者对台风风场下的铁塔结构抗风性能进行了研究[6-7]。吴新桥等在台风风场下对铁塔风振响应进行了有限元分析和测试，在台风作用下对能盘线输电铁塔进行了实时在线监测，并对比了不同风环境对铁塔风振响应的影响[8]。楼文娟等研究了不同风场下的气动响应和风振系数，并将试验结果和理论计算进行了分析对比，验证了数值分析的适用性[9]。山区地形对风荷载有较大影响，因此，特定区域输电铁塔的抗风设计还须考虑风场经过复杂微地形时的变化问题。然而台风风场经过微地形后会发生风场畸变，其对铁塔风振系数的影响，目前还尚未得到很好的分析与研究。

本文以漳泉Ⅰ/Ⅰ路沿线某处山脊为研究对象，研究台风风场下山脊风速变化特性，模拟风速时程加载到铁塔有限元模型上进行动力时程分析，计算得到铁塔风振系数并与良态风场进行对比，为台风风场下微地形区域铁塔抗风设计提供一定的参考。

1 倒塔状况及原因分析

台风“莫兰蒂”造成漳泉Ⅰ/Ⅰ路5基铁塔倒塔，倒塔区域所处位置为厦门沿海滩涂平原向山区过渡的第一重山的迎风山脊，山脊走向与铁塔线路垂直。根据福建省气象局气象站资料，在漳泉Ⅰ路#126、#127等铁塔倒塔断线过程中，附近各气象站的实测主导风向与漳泉Ⅰ/Ⅰ路倒塔段线路夹角接近90°。#126～#127等铁塔设计风速V10=34m/s，是在临近气象站所测历年 10m高度最大平均风速（31m/s）的基础上增大10%。在5基铁塔中，漳泉Ⅰ路#127塔位于山脊顶端，基础以上塔身整体失稳破坏，在垂直线路方向上倒塔，分析原因可能是风速经地形加速后超限引起的铁塔倒塌；漳泉Ⅰ路#126塔位于半山坡，塔头瓶口位置以上发生破坏，塔头曲臂在导线牵拉方向被拉倒，分析原因可能是在#127塔倒塌后顺线路方向拉扯和风荷载共同作用导致#126塔塔头破坏。漳泉Ⅱ路破坏情况如图1所示。

图1 漳泉Ⅱ路破坏情况

2 微地形Fluent风场研究

2.1 地形提取与建模

本文选取漳泉Ⅰ路#126塔和#127塔作为分析对象，#126塔位于半山坡，#127塔位于线路沿线山脊最高处。由于铁塔所在位置未设置气象监测点，导致本处铁塔的历年最大风场特性无法直接获取。因此提取一定尺度的该处山脊地形，以近地可获取的气象风场数据作为山脊地形输入风速，对风场经过山脊微地形后到达铁塔位置的风速变化进行研究。实际地形及模型如图2所示，长宽均为2km，模型最高点与最低点垂直高度约为 0.6km，临近气象站在山脊底部，与线路垂直距离约为1.5km。

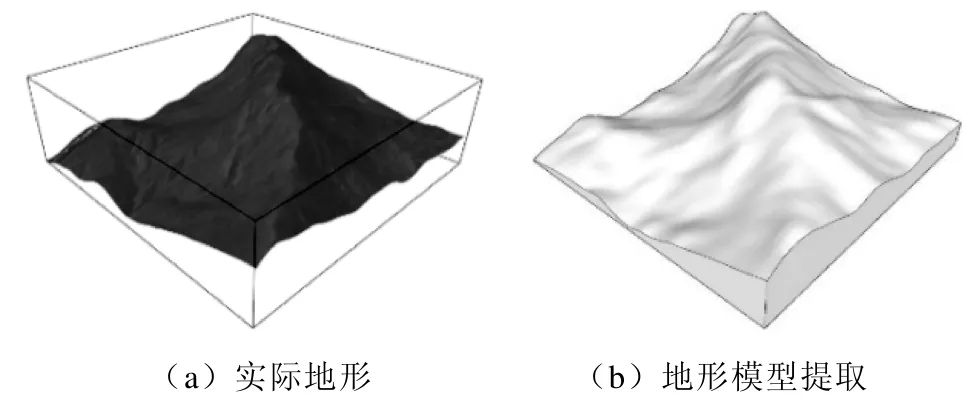
图2 实际地形及模型

2.2 微地形Fluent风速剖面仿真

根据临近气象站1985～2018年实测资料统计，10min平均风速最大值为31m/s（“莫兰蒂”台风），为仿真10m高度入口基准风速，台风风场风剖面幂指数α取 0.12，根据主导风向和铁塔线路走向，风向角为垂直线路方向。图3为入口风速和仿真完成后铁塔位置处的风速对比，由图可知：①#126塔风速最大值在塔头部位，#127塔风速最大值在塔身最下部位；②台风经过该山脊后，不同高度层风速普遍增大，40m高度以下#127塔处平均风速大于#126塔，#126塔和#127塔10m高度风速加速比分别为1.41和1.56；③漳泉Ⅰ路#126塔和#127塔处风剖面特征有较大差异，其中，#127塔的风剖面不再遵循指数律分布。漳泉Ⅰ路#127塔处于山脊顶端，其风剖面的特异性体现了微地形处湍流强度的特异性。

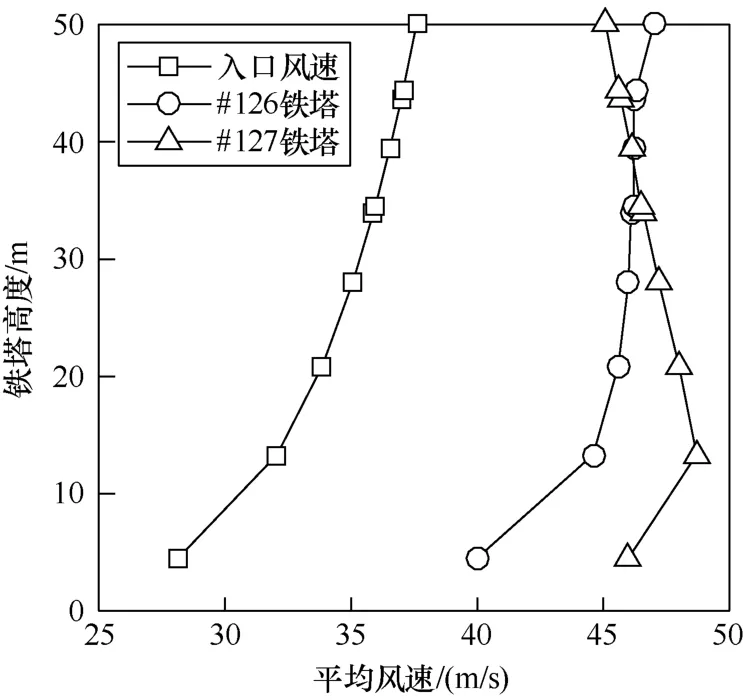
图3 入口风速和CFD仿真出口风速

3 铁塔模型建立和风速时程模拟

3.1 铁塔有限元模型

ZMV522铁塔塔高45.5m，呼高33m，在Ansys软件中建立铁塔有限元模型，如图4（a）所示。对铁塔有限元模型进行模态分析，所得铁塔前两阶模态分别为沿横担方向和沿线路方向平动模态，第三阶模态为结构的扭转振动模态，模态频率依次为2.03Hz、2.06Hz、2.76Hz，其一阶模态与漳泉Ⅰ路倒塔耐张段线路主导风向和Fluent仿真风向一致。ZMV522铁塔具有多个横担和横隔面，致使塔段质量和挡风面积发生突变，因此在计算铁塔风荷载时，为准确分析铁塔各部分静动力特性，根据铁塔组装图将铁塔沿高度简化为分段加载模型，如图4（b）所示，各塔段风荷载均匀分布在各塔段节点。

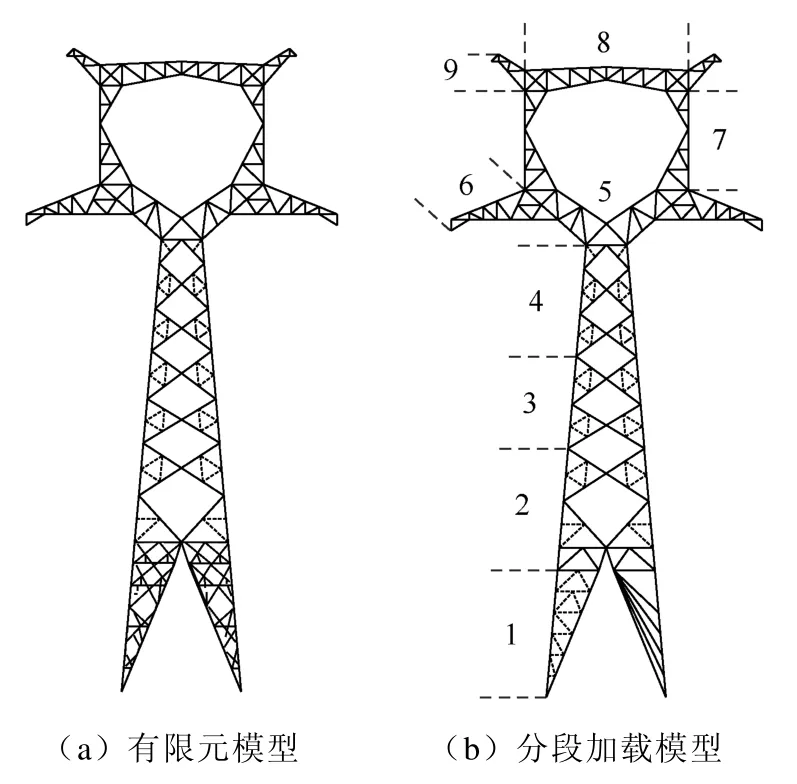
图4 铁塔有限元及分段加载模型

3.2 风速时程模拟

在Ansys环境中对铁塔进行动力分析需要模拟脉动风，以线性滤波法中的自回归数值方法模拟脉动风速，采用石沅台风谱作为风功率谱[10-11]，即

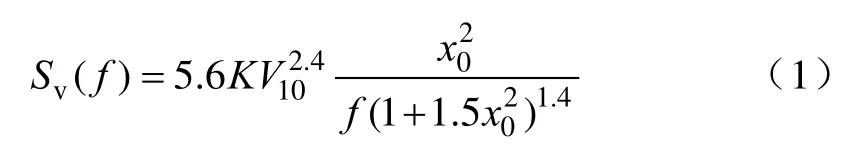
式中：K为地面粗糙度系数；x0=1200f/V10；f为频率（Hz）；V10为10m高度平均风速（m/s）。

湍流强度为脉动风速的标准差σz与平均风速Vz之比，即Iz=σz/Vz。根据DL/T 5551—2018《架空输电线路荷载规范》可知，在B类地形良态风场下，Vz=V10(z/10)α，Iz=I10(z/10)-α，则有

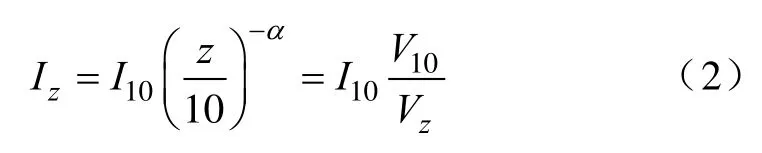
式中：Iz为离地高度为z时的湍流强度；I10为10m高度名义湍流，按B类地区取0.14；Vz为离地高度为z时的平均风速；V10为10m高度平均风速。台风风场10m高度湍流强度参考R. N. Sharma[12]基于实测得出的计算公式为ITY10=1.48I10，则台风风场湍流强度沿高度分布公式为

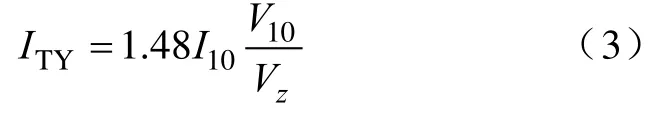
式中，ITY为山脊地形台风风场下不同高度处的湍流强度。在根据风功率谱模拟台风风场下山脊处的风速时程时，需要保证模拟得到的不同高度层风速湍流强度与ITY一致。

风速模拟过程中考虑脉动风速竖向空间相关性，#126和#127两处铁塔位置10m高度风速分别为43.7m/s和48.8m/s。图5为采用石沅台风谱模拟得到的#126铁塔在34m高度处的风速时程曲线和风功率谱对比图，脉动风模拟谱与目标谱吻合，图 6所示#126塔、#127塔湍流强度模拟曲线与目标曲线分布较为一致，验证了脉动风模拟的准确性，#126塔、#127塔湍流强度沿高度分布曲线趋同于其风剖面曲线。

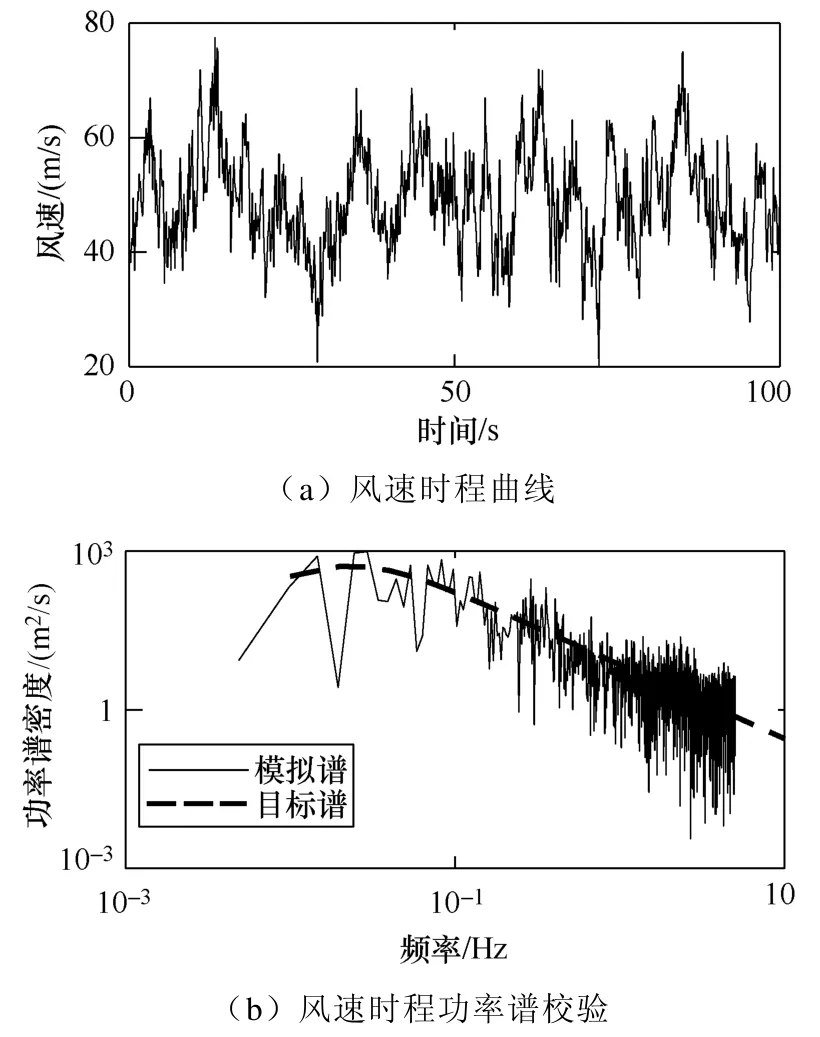
图5 #126铁塔34m高度处风速时程和校验谱

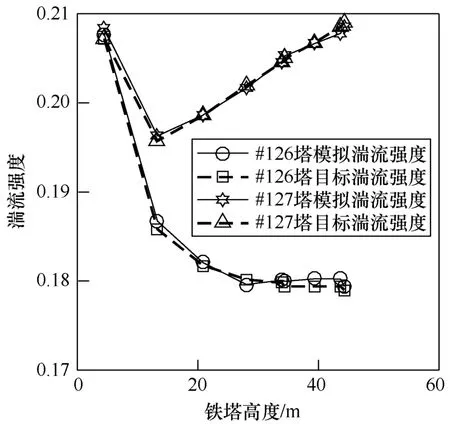
图6 台风风场下两处铁塔湍流强度对比

4 铁塔风振系数及应力比计算

4.1 动力响应特性分析

通过风速风压关系计算铁塔各塔段风荷载，加载到铁塔有限元模型的相应节点上进行瞬态动力分析。图7为两处铁塔各塔段加速度响应方均差，#127塔加速度方均差普遍大于#126塔，这是由于#127塔不同高度层湍流强度普遍大于#126塔，表明在同一风场下山顶位置相比半山坡位置对铁塔风振影响更大。

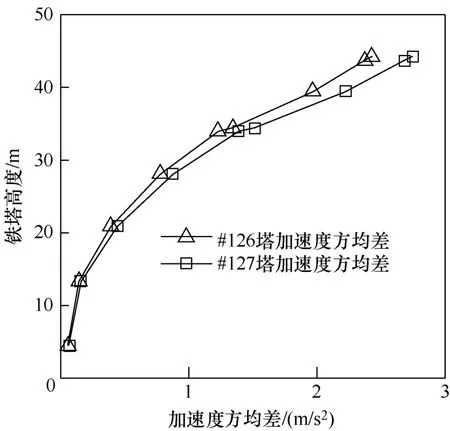
图7 不同塔位铁塔加速度方均差对比

4.2 铁塔风振系数计算

计算铁塔风振系数时可采用时程响应法，在Ansys环境中对铁塔进行风振响应时程分析，根据动力时程计算结果，铁塔z高度处风振系数βi（i为铁塔分段，i=1, 2,…,n）为[13]

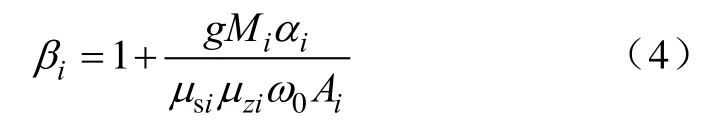
式中：Mi为铁塔分段质量；ω0为基本风压，ω0=v2/1600，v为基准风速；μzi为铁塔z高度处风压变化系数；αi、μsi、Ai分别为第i塔段加速度方均差、风荷载体型系数和挡风面积；g为峰值因子，取值为2.5。

据DL/T 5551—2018《架空输电线路荷载规范》第6.2.3条可知[14]，在仅考虑铁塔第一振型时的风振系数βz一般公式为

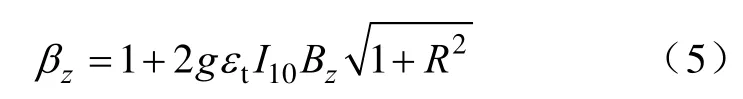
式中：εt为铁塔风荷载脉动折减系数，当铁塔全高大于40m时取值为1；I10为10m高度湍流强度；Bz为背景因子；R为共振因子。

由式（4）和式（5）计算铁塔在各类风场下的风振系数，其结果如图8所示。由图8可知：①同一风场下，DL/T 5551—2018法计算结果普遍大于时程响应法，相对较为保守，两种方法所得结果值沿高度分布较为一致，在塔头处铁塔风振系数发生多次突变，塔段8风振系数相对于其他塔段较大，这是因为该段为横担，节点板等连接固件较多，致使塔段8质量较大；②相对于B类地形良态风场，山脊地形台风风场下铁塔风振系数有较大增加，且#127塔风振系数稍大于#126塔，与Fluent风场仿真结果相对应，在两微地形铁塔位置处，DL/T 5551—2018法所得风振系数分布特征同时程响应法一致，验证了微地形台风风场下铁塔风振系数计算的准确性。

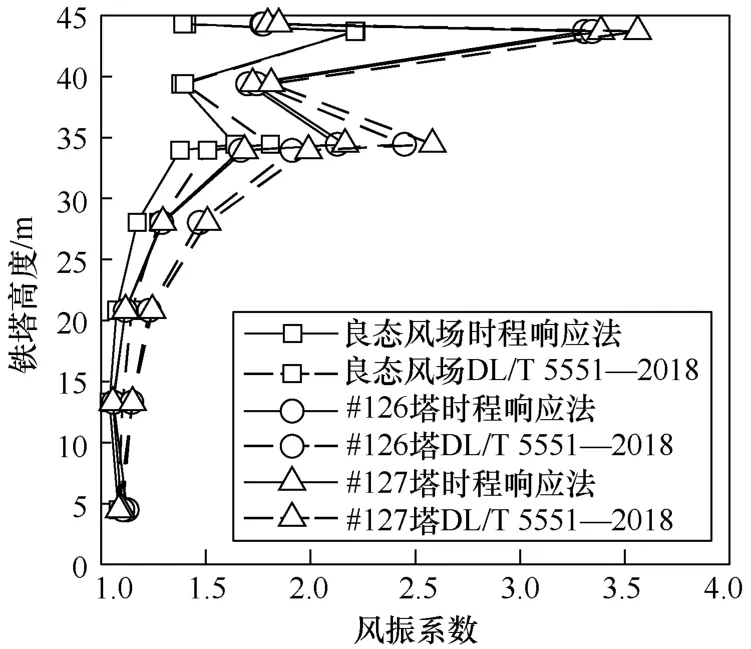
图8 漳泉Ⅱ路铁塔风振系数

为更好地比较两处铁塔风振系数的大小，分析风场对铁塔的影响，沿高度分别计算不同方法下铁塔在不同工况时的风振系数加权平均值。由表1和表2可知，相对于B类地形良态风场，山脊地形台风风场下#126塔、#127塔时程响应法所得加权平均值分别增加14.5%、16.1%，DL/T 5551—2018法所得加权平均值分别增加17.7%、20.0%。不同计算方法所得结果表明，山脊地形台风风场对铁塔风振响应有较大影响，在铁塔抗风设计时必须考虑台风高湍流和微地形双重因素引起的风振增大效应；DL/T 5551—2018法所得加权平均值相比时程响应法较大，这是因为DL/T 5551—2018法取值较为保守，也进一步验证了该方法在微地形台风风场下的适用性。

表1 铁塔风振系数加权平均值

表2 加权平均值增加比（相对良态风场）

4.3 应力比计算

应力比指效应与承载能力的比值，在这里可以通过计算各杆件实际应力与设计应力的比值来衡量铁塔抵抗风荷载的能力，有限元铁塔模型的各杆件材料应力由两部分产生：①由风振系数计算得到的铁塔等效静风荷载；②导地线及绝缘子串对铁塔产生的荷载。铁塔等效静风荷载计算式为

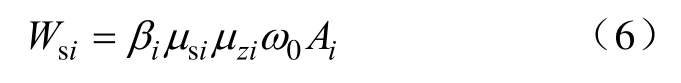
式中：Wsi为各塔段等效静风荷载，其他参数意义同前。在铁塔的抗风设计中，将风对铁塔的复杂动载成分通过风振系数转化为静载作用。将导地线和绝缘子串视作铁塔的一部分，通过同样的原理方法计算风对导地线及绝缘子串的等效静风荷载，加载到相应的横担节点上。在Ansys环境中加载完成后，计算#127塔和#126塔的应力比，其云图如图9所示，杆件粗实线所标位置为应力超限区域。

#127塔在台风工况下的应力比如图 10（a）所示，整塔杆件应力比范围为 0.695～2.133，比值大于1表明原设计杆件不足以承受微地形台风工况下的外力。其中，塔段7瓶口位置杆件最大应力比为2.133，且为受拉控制，该杆件率先破坏；塔段2主材应力比最大为1.746，且为受压稳定控制，可判断该段主材率先失稳，进而引起上部杆件的连续性失稳破坏。因此，分析判断#127塔，在垂直线路风向作用下，塔段2主材局部受压失稳最先出现破坏，从而引起结构整体失稳破坏，倒塌方向与垂直线路风向吻合，即与线路方向垂直。

图9 应力比云图

图10 应力比数据

#126塔在台风工况下的应力比如图10（b）所示，整塔杆件应力比范围为 0.563～1.737，主材应力比最大处仍为塔段2，塔头最大应力比为1.737，通过分析可以看出，台风作用下，#126塔的破坏形态应与#127塔类似，即整体倒塌，但#126塔位距离台风中心较#127塔更远、风速相对较小，当#127塔先行破坏时，拉扯导线，导线的张力作用在#126塔头，和风荷载共同作用下，导致曲臂失稳破坏。两处铁塔的风振分析结果与实际倒塔现状较为吻合，验证了Fluent仿真、铁塔动力响应分析和风振系数计算全过程。

5 结论

本文以漳泉线路铁塔为研究对象，分析计算其在山脊地形台风风场下的风振系数，所得结论如下：

1）微地形铁塔位置不同，铁塔位置处经地形加速后的风速不同，且风剖面不再遵循指数律分布；通过相关规范近似推算出的台风风场下山脊处的湍流强度沿高度分布公式，能够较好地应用到微地形风场风速时程模拟当中。

2）台风风场经过山脊地形后，相对于 B类常规地形良态风场，铁塔风振响应和风振系数大大增加，山脊顶端#127塔在台风风场下的风振系数相比常规地形良态风场可增加16.1%左右。

3）通过等效静风荷载的加载计算铁塔各杆件应力比，其分析结果与#126和#127塔实际倒塔现象和原因分析吻合，验证了Fluent仿真、铁塔动力响应分析和风振系数计算全过程，表明了山脊地形台风风场下时程响应方法计算铁塔风振系数的可行性。