复杂网络上的意见动力学对谣言传播的影响*

王祁月 刘润然 贾春晓

(杭州师范大学， 复杂科学研究中心， 杭州 311121)

1 引 言

近年来， 随着各种在线社交软件的兴起和壮大[1，2]， 如Twitter、微博和微信等， 互联网上的信息和谣言传播行为也引起了研究人员的极大关注[3]，特别是社交网络中谣言的爆炸性传播现象[4].在谣言和信息传播的过程中， 依靠人与人之间的好友关系所形成的信息传播网络结构对于信息的传播具有至关重要的作用， 如网络的无标度效应[5]、小世界效应[6]， 以及聚类、社团结构[7]和度度相关性[8]等， 这些网络结构性质极大地增强了谣言传播的速率[9]， 使得信息或谣言在网络上的传播过程中涌现出了非常丰富的现象[10].

在谣言传播的研究中， 最为广泛采用的两个谣言传播模型是由Daley 和Kendall[11]提出的DK模型和由Maki 和Thompson[12]提出的MK 模型.这两个模型都在考虑了信息传播动力学特征的基础上， 借鉴了Kermack 和McKendrick[13]提出的疾病传播SIR 模型.在模型中， 人群被分为三部分:不知道谣言的人 (S)， 知道谣言并传播谣言的人 (I)和知道谣言但已经停止传播的人 (R).随着网络科学的发展， 一些学者发现信息传播过程所依赖的网络是高度结构化的， 同时在时间和空间上都具备特定的规律和特性.因此一些谣言传播的研究也引入了复杂网络理论.Zanette[6]通过数据仿真的方式研究了小世界网络上的谣言传播， 发现小世界网络存在1 个断边重连的临界概率pc， 当断边重连概率p 小于pc时， 谣言被局限于传播者的周围而不能暴发; 而当p 大于pc时， 谣言能够传播到整个系统而暴发.对于度分布异质性较强的网络， 度大的节点更容易变为R 状态， 谣言相对于同质性的网络更不容易得到大范围的传播， 这一结果与疾病传播的情况恰恰相反[14].此外， 信息传播的效率问题也受到广泛关注， 通常来说无标度网络的传播效率高于随机网络， 一对一传播的效率高于一对多传播的效率[15].

在谣言传播的研究中， 识别网络中对于谣言传播具有关键作用的节点对于理解谣言的传播也具有重要的意义.文献[16]通过Maki-Thompson 模型研究了实证网络上k 核指数较大的节点对于谣言传播的作用， 发现R 状态的节点密度并不依赖于k 核指数， 这说明k 核指数较大的节点并不是好的传播者.然而在实证网络的研究中， k 核指数较大或度值较大的特权传播者是存在的， 因此后续有人提出了两种修正的信息传播模型: 第一种情况是， 当S 遇到I 时， S 以一定的概率直接变化为I，以剩余的概率直接变为R; 第二种情况是， 传播者可能处于活跃和非活跃状态两种不同状态.此外，在谣言传播动力学的研究中， 谣言传播的路径和网络结构往往是未知的， 如何获取谣言传播的路径和过程， 以及谣言传播的源头也是非常重要的问题，因此谣言传播网络的识别[17]、溯源[18]和目标传播[19]问题也受到广泛关注.

随后人们发现， 信息或疾病可能通过不同网络分别传播或者跨网络传播， 因此引入了多层网络模型来描述信息或疾病传播动力学过程[20]， 此外， 信息传播还可能与其他传播的动力学发生较为复杂的相互作用， 如竞争[21，22]和合作[23]等.文献[24]研究了信息传播对疾病传播的影响， 并且探讨了在不同网络拓扑结构下的最优传播机制.文献[25]研究了双层网络上个体的异质性对多层网络上疾病传播和个体警惕性传播的影响.文献[26]分析了带有记忆机制和遗忘机制的经典谣言传播模型， 并研究了该模型在均质网络中的动力学行为.Xia 等[27]考虑谣言内容的吸引力和模糊性， 提出了具有犹豫机制的修正SEIR 模型.Soriano-Paños 等[28]引入了1 个双层网络模型来研究社会系统中信息传播与舆论形成的相互作用.多层网络概念的引入为研究传播过程与其他动力学的相互作用提供了便利条件， 产生了极为丰富的研究成果.

在当前主流在线社会网络中， 谣言传播往往会引发舆情， 谣言的传播和舆论的形成是1 个双生话题.目前， 过去复杂网络上舆论的研究往往采用意见动力学模型， 该模型主要分为两类: 第一类为离散观点模型， 如Sznajd 模型[29]、选民模型[30]等;第二类为连续观点模型， 如边界信任模型[31，32]等.借助于这些模型， 人们从社会网络结构[33]、评价文本挖掘[34]、个体特征[35]等角度研究了舆论形成机制.谣言的传播过程亦会受到人们的判断力和他人观点的影响.一些谣言在经过网络持续发酵后， 产生了惊人的传播暴发力， 而传播的扩大化又会进一步影响舆论.而还有一些谣言， 经过公众理性辨识后， 自发在网络中传播终止了.究竟在什么情况下，谣言能够暴发？基于人群中观点的演化， 对信息传播动力学的过程进行建模， 对于我们理解谣言传播会有所帮助.然而， 如何基于意见动力学对信息传播建模， 并度量意见动力学对于信息传播进程的影响是1 个全新的问题.

社交网络中群的存在能够使得信息以广播的方式快速高效地传播， 如微信群、QQ 群以及微博，同时这些群的存在也会促使个体对信息进行封闭性讨论， 这种讨论或对信息的传播起到发酵或抑制的作用[36].本文将采用群传播的方式来对信息传播进行建模， 并基于群来探讨人群的意见会对信息传播构成的影响[37].在某些情况下， 信息的真伪是难于判断的， 这里采用类似意见动力学模型中“多数者”规则， 1 个个体是否采信某个信息取决于他所感知到的群中相信该信息的个体数量.根据这一规则， 个体意见和信息传播是相互影响的.基于此，本文结合SIR 信息传播模型和意见动力学理论，建立了在线社交网络谣言传播模型， 使其能描述社交网络上谣言传播与意见动力学的相互作用， 以期望我们的研究可以更好地理解信息传播中的复杂现象， 对丰富谣言传播理论和舆情的防控具有重要的现实意义.

2 基于意见动力学的SIR 谣言传播模型

图1 谣言传播示意图 (a) 网络有三种状态节点， S 状态、I 状态和R 状态， 图中蓝色圆圈表示其中1 个传播者I 与其邻居所构成的群; (b)， (c)传播者向在以自己为中心的群中传播信息; 在受到抑制者的影响的情况下， S 状态节点以一定概率转换成I 状态节点， I 状态节点以一定概率转换成R 状态节点; (d) 系统到达稳态， 传播停止Fig.1.Schematic diagram of rumor propagation.(a) The network is composed of N nodes with three states S， I and R.The blue circle in the figure represents the group formed by one of the spreaders I and its neighbors.(b)， (c) Spreaders spread the rumor to their self-centered groups.Influenced by the stiflers， S state node turns into I state node with a certain probability， and I state node turns into R state node with a certain probability.(d) The system reaches to a steady state and the spreading process ends.

接下来将介绍本文SIR 谣言传播模型.首先，在本文模型中存在1 个由N 个个体组成的社交网络， 在这个网络中， 个体被视为节点， 个体之间的关系被视为网络节点之间的连接.根据网络中的个体在谣言传播过程所处的不同状态， 把网络的节点细分为未知者S、传播者I 和抑制者R.类似于SIR 流行病传播模式， 未知者代表了从未听过或没有采信消息的人， 传播者代表了相信信息并能够传播的人， 移除者代表了已经知道信息但持反对态度的人.为了刻画真实网络中信息往往通过社交网络中的群进行传播的特征， 在本文SIR 模型中， 假设每个个体都和他的最近邻形成1 个信息传播群， 信息通过群进行传播， 个体也可以在群内对信息进行评论或发表自己的看法.在信息传播的初始阶段只有少数比例的个体i (t = 0)是传播者， 同时也有少数比例的个体r (t = 0) 是抑制者， 而其余比例的个体是未知者s (t = 0).采用蒙特卡罗模拟方法对系统进行模拟， 在每1 个时间步， 系统以如下规则进行演化:

1)首先， 随机挑选1 个个体， 如果该个体不是传播者， 进行下个时间步的演化， 否则这一个体将信息转发至以他自己为中心的群中(群由传播者和其直接相连的节点构成)， 群中抑制者会以概率γ选择保持沉默， 以概率1— γ 选择进行评论并发表自己对信息的怀疑看法， 试图影响群中其他个体.

2)未知者接收到消息后会以概率 λ =γm转换成传播者.其中m 代表群中抑制者的个数.在给定抑制者数量m 的情况下， 抑制者的沉默概率 γ 越大， 未知者转变为传播者的概率就越大; 同时在给定抑制者的沉默概率 γ 的情况下， 群中抑制者数量m 越大， 未知者转变为传播者的概率就越小.

3)群中的传播者也会受到抑制者评论的影响，从而对信息的真实性产生怀疑， 即每1 个传播者以1-λ 概率转换成抑制者， 以概率 λ 保持不变.

规则1)描述了信息在网络中的传播过程， 以及个体之间对信息的讨论过程.规则2)和3)则描述微观层面上信息传播与个体观点的相互作用机理.这3 个规则是基于现实热点舆情案例的抽象，即传播者最初将信息转发朋友圈、微信群或微博，然后引发网友的关注、评论和讨论， 这些讨论和评论又会促使部分网友转发给更多的人， 从而引发更多的评论和传播[38].考虑现实中， 传播者对他所收到的信息总是在有限的时间内保持激活的状态， 即传播者通常不会在1 个群中多次转发同一信息.在该模型中， 假定每个传播者只能传播1 次谣言.当所有的个体不再传播谣言时， 系统达到稳定状态.通常来说未知者的数量在系统中是非常重要的[39]，可以度量没有受到谣言传播和影响的个体数量.本文用稳态传播者的比例或抑制者的比例来度量谣言传播的范围.谣言传播示意图如图1 所示.

3 数值模拟结果与分析

3.1 ER 随机网络

图2(a)表示当 γ =0.4 时， ER 网络上SIR 三种状态节点占比随时间的演化.在谣言传播的早期， 研究发现传播者增加速度较快， 而抑制者却几乎没有增加.这说明在谣言传播的前期， 谣言的传播处于一种较为自由的方式， 大量的未知者收到谣言后迅速转变为传播者.由于此时传播者没有遇到抑制者， 抑制者的群体规模几乎保持不变.到了谣言传播的后期， 传播者群体规模已经变得较为庞大， 其中一部分传播者遇到抑制者后会被转变为抑制者.此时， 传播者的群体规模开始下降， 而抑制者群体规模开始突然上升， 同时未知者群体数量在抑制者和传播者的互相制衡下到达了稳定的状态.这一结果说明， 本文谣言传播模型所描述的动力学过程以传播者群体规模的峰值位置为界可以分为两个阶段， 第1 个阶段为谣言自由传播的前期， 第2阶段为抑制者和传播者互相制衡的后期， 当第2 阶段结束后系统到达稳态.

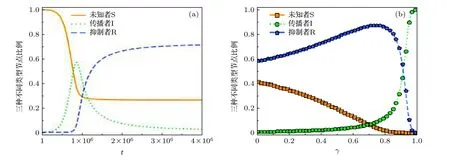
图2 (a) ER 网络上SIR 三种状态的节点比例随时间的演化图， 沉默概率 γ =0.4 ; (b) ER 网络上稳态SIR 节点比例随 γ 值的变化图， 图中曲线来自于网络规模为N = 1 × 106， 平均度为10 的ER 随机网络， 初始传播者和抑制者的比例均设为0.1%.图(b) 中的数据来自于演化时间t = 4 × 106 时的结果Fig.2.(a) Time evolution of the fractions of nodes with different states on ER network， where the silence probability γ is equal to 0.4; (b) the steady fractions of nodes with different states as a function of γ on ER networks.The curves in the figure come from the ER random network with a size N = 1 × 106 and an average degree of 10.The fractions of both the initial spreaders and the stiflers are set as 0.1%.The data in panel (b) are from the simulation results for t = 4 × 106.

图2 (b)给出了ER 随机网络上SIR 三种不同群体的个体的稳态规模随沉默概率 γ 的变化.可以发现， 抑制者数量与沉默概率 γ 之间呈现出非单调的函数关系， 即随着 γ 的不断增加， 抑制者的比例先增后减.将抑制者比例的峰值位置记为 γc， 这是抑制者数量随γ 的变化从增加到减少的转折点.在γc所在的位置， 未知者的群体规模和传播者的群体规模也存在显著变化.在参数 γ ＜γc时， 未知者节点规模随着 γ 值的增加呈现单调递减趋势， 在 γ 趋近于 γc时， 已经接近零值; 传播者规模在参数γ ＜γc时， 一直处于非常低的水平， 在当 γ 接近于 γc时，网络中的传播者节点数量迅速上升.由此可以看出， γc可以看成系统中谣言暴发的阈值， 当γ ＜γc时， 谣言可以较好地受到抑制者的控制而不能暴发;当 γ ＞γc时， 抑制者将不能控制谣言的传播， 从而导致传播者的数量在系统中暴发式地增长.

图3 给出了不同沉默概率下SIR 三种不同状态的节点数量随时间的演化情况.可以看到， 在传播的前期， 由于传播者未遇到抑制者， 传播者在系统中以一种较为自由的方式增加， 网络中传播者在早期增长的趋势与 γ 无关(见图3(b))， 同时未知者随时间的推进而减少的趋势也与参数 γ 无关(见图3(a))， 而抑制者在此时的规模也不会有显著的变化(见图3(c)).但到了后期， 传播者会受到抑制者的影响， 沉默概率 γ 越大， 稳态未知者的数量就越小， 传播者数量的峰值就越大， 后期减少的趋势就越缓， 抑制者开始增加的阈值就越大.这一结果揭示了ER 网络上该模型谣言传播的动态特性， 在传播前期， 谣言具有自由传播的现象， 在当传播者的规模到达一定程度时， 抑制者才能感知到谣言并对谣言的传播产生干预和影响.对于 γ =0.3 和γ =0.6这两个特例， 由于沉默概率较低， 谣言被抑制者有力地控制住了， 传播者在稳态保持了较低的比例.而对于 γ =0.9 的情况， 抑制者由于不能控制谣言的传播， 传播者在稳态仍然有较高的比例.

3.2 无标度网络

在无标度网络上谣言传播的研究中， 首先生成1 个满足幂率分布而且平均值为10 的度序列，其中最小值为5， 最大值为60， 幂指数为—2.5， 然后采用配置模型来生成无标度网络.图4(a) 给出了在 γ =0.4 时无标度网络上三种状态的节点比例随时间的演化.与ER 随机网络类似， 无标度网络中SIR 三种状态的节点比例具有类似的变化趋势， 传播者I 节点数量在不同 γ 参数值下也出现了峰值现象.相比于ER 随机网络， 传播者I 节点数量的峰值出现得较早， 这说明谣言在无标度网络中前期自由传播阶段持续时间较短.这是因为无标度网络度分布的异质性较强， 传播者和抑制者都能够较快地占据网络的中心节点， 在谣言未得到充分传播之前二者能够较快地发生相互作用， 从而使系统中大量的度值较小的节点不能较快地接触到信息.因此，谣言更不容易在无标度网络中扩散， 表现谣言自由传播的前期持续时间较短， 同时网络中未知者的比例也较大(由图2(a)和图4(a)的比较可知).这说明无标度网络度分布的异质性对于谣言的传播具有抑制作用.

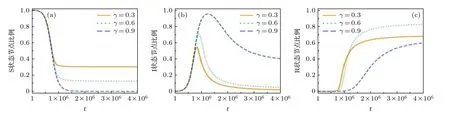
图3 ER 网络上不同沉默概率 γ = 0.3， 0.6， 0.9 下SIR 三种不同状态节点的比例随时间演化图 (a) S 态; (b) I 态; (c) R 态; 初始传播者和抑制者的比例均为0.1%， ER 网络的平均度为10Fig.3.Time evolution of the fractions of nodes with different states on ER random networks with different silencing probability γ =0.3， 0.6 and 0.9: (a) State S; (b) state I; (c) state R.The initial fractions of spreaders and the stiflers are both 0.1%， and the average degree of the ER network is 10.

图4 (a)无标度网络上SIR 三种状态的节点比例随时间的演化图， 沉默概率 γ =0.4 ; (b)无标度网络上稳态SIR 节点比例随γ值的变化图， 图中曲线来自于网络规模为N = 1 × 106， 平均度为10 的无标度网络， 初始传播者和抑制者的比例均为0.1%， 图(b)中的数据来自于演化时间t = 4 × 106 时的结果Fig.4.(a) Time evolution of the fractions of nodes with different states on scale-free networks， where the silence probability γ is equal to 0.4; (b) the steady fractions of nodes with different states as a function of γ on scale-free network.The curves in the figure come from the scale-free network with a network size of N = 1 × 106 and an average degree of 10.The fractions of both the initial spreaders and the stiflers are set as 0.1%.The data in panel (b) are from the simulation results for t = 4 × 106.

图4 (b)为无标度网络中SIR 三种状态节点在不同的参数 γ 下的比例曲线图.相对于ER 随机网络， 抑制者节点数量的峰值所对应的阈值 γc较大(由图2(b)和图4(b)的比较可知).这一结果再次证实了无标度网络度分布的异质性对谣言传播的抑制作用， 这一结果与文献[13]的结果一致.图5展示了无标度网络中SIR 三种状态节点在不同的参数 γ 的情况下随时间的演化， 这一结果与ER 网络的情况类似， 但是自由传播阶段持续时间较短(由图3(b)和图5(b)的比较可知)， 再次证实了无标度网络度分布的异质性能够使抑制者较早干预传播者对谣言的传播， 这也证实了两个不同的谣言传播阶段的特性.

3.3 真实网络的模拟结果

为了了解真实社交网络拓扑如何影响传播动力学， 图6(a)和图6(b)给出了对Facebook 和Gowalla 网络得到的网络样本数据的模拟结果.Facebook 数据提取于2017 年11 月， 其中22470 个节点代表政治家、政府组织、电视节目和公司四类主体的页面， 171002 边代表这些页面之间的相互关注.Gowalla 是1 个区域性社交网络， 其中含有196591 个用户， 950327 条边代表这些用户之间的朋友关系.Facebook 网络和Gowalla 网络度分布如图6 所示， 可以看出二者累积度分布的尾部非常接近于幂率分布.

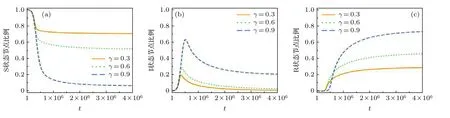
图5 无标度网络上不同沉默概率 γ = 0.3， 0.6， 0.9 下SIR 三种状态节点的比例随时间演化图 (a) S 态; (b) I 态; (c) R 态; 初始传播者和抑制者的比例均为0.1%， 网络平均度为10Fig.5.Time evolution of the fractions of nodes with different states on scale-free networks with different silencing probability γ =0.3， 0.6 and 0.9: (a) State S; (b) state I; (c) state R.The initial fractions of spreaders and the stiflers are both 0.1%， and the average degree of the scale-free network is 10.

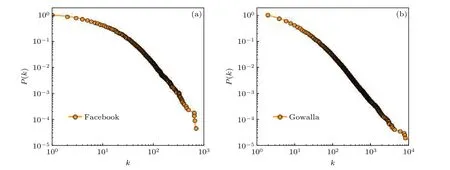
图6 Facebook 网络(a)和Gowalla 网络(b)在双对数坐标下的累积度分布P(k)Fig.6.Cumulative degree distribution of Facebook network (a) and Gowalla network (b) in logarithmic coordinates.

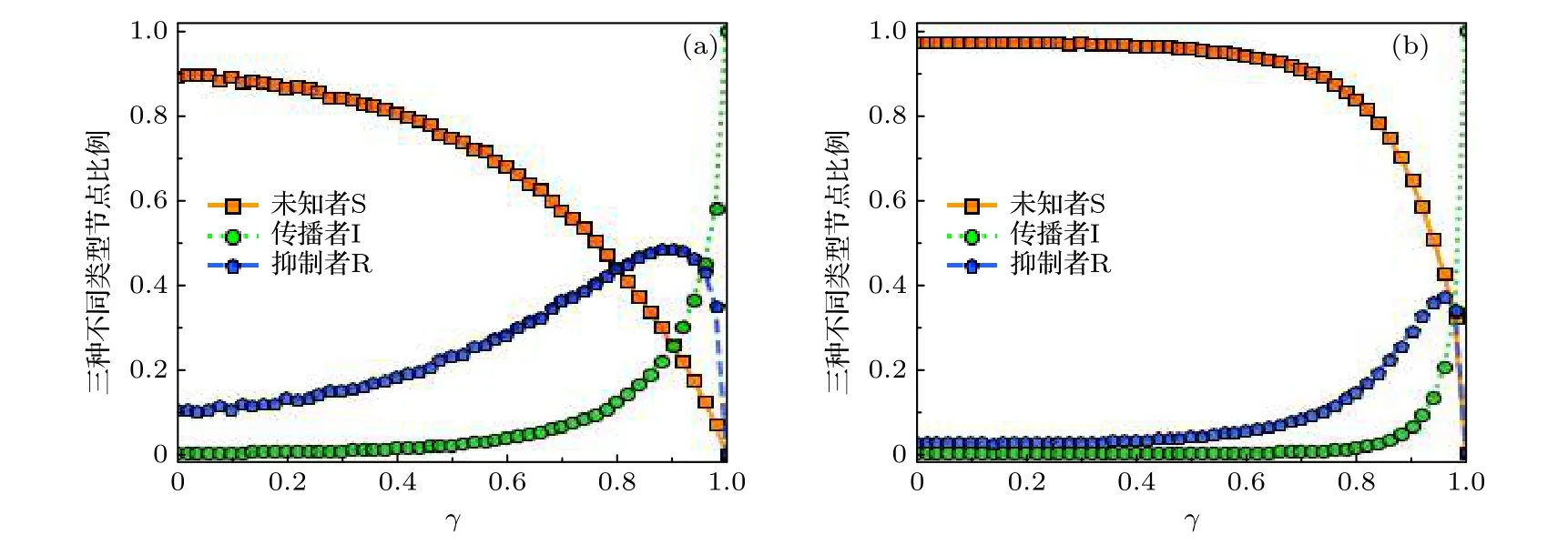
图7 Facebook 网络(a)和Gowalla 网络(b)稳态SIR 三种节点比例随不同 γ 值的变化; 在数值模拟中， 初始传播者和抑制者的比例均设为0.1%; 图(b) 中的数据来自于演化时间t = 4 × 106 时的结果Fig.7.Steady fraction of nodes with different states as functions of γ on Facebook network (a) and Gowalla network (b).In the numerical simulations， the initial fractions of spreaders and the stiflers are both 0.1%.The data in panel (b) are from the simulation results for t = 4 × 106.

将这两种网络作为个体相互作用的结构来对本文模型进行数值模拟.图7 给出了两个网络上稳态三种不同节点的比例.可以看出， 抑制者比例峰值出现的位置较大， 这与SF 网络的结构接近， 同时上述描述的抑制者数量的非单调现象依然存在.这一结果表明， 在真实的网络上， 同样存在谣言暴发的阈值 γc， 通过控制模型抑制者的沉默概率可以避免系统中谣言的暴发.

4 结果与讨论

为了更好地描述真实在线社交网络的谣言传播过程， 本文提出了一种新的基于个体意见的谣言传播模型.与标准SIR 模型不同的是， 该模型考虑到了谣言传播和个体意见之间的交互作用.传播者I 主导着系统中谣言扩散的动力学过程， 通过对谣言的传播来促使更多未知者S 相信并传播谣言;而抑制者R 通过对谣言的评论试图使人们不信谣言或者放弃传谣来对抗谣言的传播.在模型中， 存在1 个关键可调参数 γ 控制着抑制者在收到谣言时的沉默概率.首先， 研究发现在沉默概率阈值以下， 沉默概率的变化对传播范围的影响较小， 而当沉默概率超过阈值时， 谣言的传播范围将会暴发式增长.抑制者节点数量与沉默概率存在非单调关系， 即随着 γ 值的不断增加， 抑制者R 的节点比例先增后减， 存在峰值.这一现象为定位谣言的暴发阈值提供了有用的信息.其次， 我们发现整个谣言传播动力学过程存在两个关键阶段， 在前一个阶段， 谣言在网络中自由传播， 在后一个阶段， 抑制者和传播者互相制衡并达到稳态， 这两个阶段以传播者数量的峰值为分界线.这一结果为理解网络上的谣言传播行为提供了有用的信息.再次， 比较了无标度网络和ER 随机网络上的谣言传播动力学过程的不同特征.对于无标度网络， 谣言暴发的阈值 γc大于ER 随机网络， 谣言传播的范围也小于ER 随机网络， 这说明无标度网络度分布的异质性对谣言的传播存在抑制作用: 由于度值较大的中心节点的存在， 使得传播者更容易占据中心节点， 促使抑制者较早地和传播者发生相互作用从而制约了传播者对谣言的传播.最后， 在真实的Facebook和Gowalla 社交网络中采用本文模型进行了数值试验.仿真结果表明， 在真实社交网络中， 抑制者数量和沉默概率之间的非单调关系仍然存在.这些结果为舆情防控提供了有力理论依据和启发.因此， 如何引导人们抵制有害信息的影响， 营造良好的网络文化氛围是非常重要的.根据本文研究， 可以得出: 减小抑制者的沉默概率可以有效地控制谣言的传播范围.

考虑现实中也存在未知者在听到辟谣信息后直接转化成抑制者的可能， 我们也曾研究了模型规则2)的另一种情况， 即当未知者接收到辟谣消息后会以概率λ = γm转换成传播者， 以1－λ 的概率转变为抑制者.这一修改版本的模型与正文所介绍的模型在定性的结果上存在相似性.但是， 本文研究工作对整个社交网络尚有不足之处， 如传播者只能传播1 次谣言， 在考虑传播者能够多次传播信息的情况下， 结果又会如何？另外， 对于一些真实的社交网络， 参与讨论的人群是能够动态变化的，在这种情况下， 谣言又会以何种方式传播？这些问题以及模型的理论解析都值得今后进行进一步的思考与研究.