一种自适应分数阶微分的改进SIFT算法
2021-03-25周虹
周虹


摘 要:图像特征具有低对比度、平滑梯度的产品表面缺陷,与表面背景图案和污渍十分接近,这对基于机器视觉的缺陷识别和检测带来严重干扰。该文提出一种改进SIFT算子的特征识别方法,用分数阶微分代替高斯差分算子,再利用圖像局部梯度和信息熵,自适应生成分数阶微分次数,有效克服SIFT无法有效提取污渍、纹理等低对比度特征的缺陷。实践证明,该方法能在复杂干扰环境下实现对特定缺陷的识别,且具有较高的检出速度、检出率以及工程实用价值。
关键词:SIFT 表面检测 分数阶微分 缺陷识别
中国分类号:TB486;TQ174.76;TP391.41 文献标识码:A文章编号:1672-3791(2021)01(c)-0010-05
Abstract: The image features have low contrast, smooth gradient of the product surface defects, and the surface background patterns and stains are very close, which brings serious interference to machine vision based defect recognition and detection. This paper proposes an improved feature recognition method for SIFT operators, which uses fractional differential instead of gaussian differential operator, and then uses image local gradient and information entropy to generate fractional differential times in an adaptive way to effectively overcomes the defects SIFT can not effectively extract low contrast features such as stains and textures. Practice has proved that this method can realize the identification of specific defects in complex interference environment and has high detection speed, detection rate and engineering practical value.
Key Words: SIFT; Surface detection; Fraction differential; Defect recognition
表面缺陷是影响产品品质的重要指标之一,主要包括裂纹、针孔、印刷缺陷、斑点等。
近年来,基于机器视觉的表面缺陷自动检测研究越来越受关注,并取得了一定的进展[1-3],文献[1]利用阴极铜板的缺陷颜色和背景有较大差别,设计了一种基于彩色空间的聚类方法以实现快速区分缺陷的目的,但该方法受光照影响大,且无法有效利用基于灰度空间的大量成熟算法,计算效率低;文献[2]介绍了一种基于频域滤波的方法,对裂纹检测取得了较好效果,但此方法在有干扰的情况下无法拓展到其他缺陷检测;文献[3]利用多特征融合以及卷积神经网络,实现了金属板带材表面缺陷的检测,但该方法同样只适用于无干扰的情况下。
目前,陶瓷料、木料等产品表面缺陷的视觉检测在生产实际中应用依然较少,这主要是因为生产环境中的干扰因素比实验室要多。以瓷砖为例,一是瓷砖表面缺陷形态各异,没有统一的形状和尺寸作为模板;二是瓷砖表面留下的水渍、碎石、手印等,和缺釉、斑点在图像上非常相似,会对视觉检测带来严重干扰,对于中小企业而言,这些干扰又很难在视觉检测前彻底清除。此外,位置变化、光照不均等因素也会影响缺陷的检测。在这样复杂干扰环境下,传统的基于颜色信息统计或者基于标准模板对比的简单视觉检测方法往往都得不到理想的效果。
基于SIFT特征点匹配的缺陷识别算法,可以有效克服以上不足,在复杂干扰环境下能实现快速、准确识别缺陷的目的。文献[4]成功运用SIFT对中厚板的表面缺陷进行了检测,识别准确率达到95%;文献[5]将SIFT算法用于药用玻璃瓶印刷字缺陷的检测,并取得了较好的检测结果;文献[6]在汽车保险盒的在线缺陷检测中,成功运用了SIFT算法,并得到了理想的实验结果。
1 基于分数阶微分的改进SIFT算子
近年来,分数阶微分(Fraction differential)在图像处理上的应用越来越受到关注。分数阶微分能利用非局部信息来计算像素微分,在低对比度边缘和纹理边缘识别中具有优越的性能。
目前,典型的分数阶微分定义主要有两种,一种是G-L(Grunwald-Letnikov)方程,另一种是R-L(Riemann-Liouville)方程。R-L方程更适合于数值计算,因此该文采用R-L方程结合SIFT算子进行研究[7]。
R-L分数阶微分方程定义如下:
式中,I为分数阶微分代号,[g,h]为自变量t的取值范围,α为微分次数,Γ(α)为伽马函数,定义如下:
对于图像的边缘等高频部分,1~2阶之间的分数阶微分算子对轮廓的提取虽不及2阶微分算子强,但比1阶微分的增强效果要好。而对于纹理、水渍等图像低频部分,0~1阶分数阶微分有效改善了1阶微分对于边缘信息衰减严重的问题。因此,分数阶微分提高了高频信息,而且没有使中低频图像信息过分衰减,从而改善了SIFT提取图像纹理和低对比度细节信息的能力[8-9]。
基于分数阶微分的特点,理想的微分次数应该是:对于高频图像特征,次数接近2,对于低频特征,次数接近0。如果能让次数α自适应变化,则能具备最佳特征提取效果。接下来的问题是如何判断图像区域是边缘区域还是纹理或者平滑区域。
梯度具有判别边缘的能力,而信息熵具有判别纹理的能力,于是我们的办法是结合梯度和信息熵来进行判断。
最后分析分数阶微分次数与综合判别因子之间的关系。从前面的分析可以得出α的范围是[0,2],且趋势是逐渐接近。于是该文采用反正切函数来拟合这个关系。并且,综合判定因子虽然综合了梯度和信息熵,但是梯度占主要部分,因此综合判定因子也就用频率来近似。
经过反复实验,我们得到α和f的函数关系为:
2 基于改进SIFT算子的瓷砖表面缺陷检测
SIFT算子的关键在于特征点选取,由于充分考虑了缩放、尺度、旋转等因素影响,从而可以实现有干扰的环境下准确地识别出缺陷。但该算法计算流程复杂、数据处理量大、检测耗时较长的缺点,导致其在实时检测场合的应用受限。直接的解决思路是在保证检测精度的前提下,尽可能减少特征点的数量,从而有效压缩最终的特征描述矩阵。而减少特征点数量的有效辦法是针对具体应用场景优化SIFT算子的各个参数。
2.1 图像金字塔组数的确定
关于组数(Octave)的确定,Lowe在其论文中给出了一个经验公式[7]:
式中,p为待求组数;m,n为图像尺寸大小;a为修正值,取值范围为[0-p],具体可根据金字塔图像的尺寸范围来确定。
以瓷砖表面缺陷检测为例,按照国家标准,瓷砖表面缺陷的检测要求是在距离1 m的瓷砖上方观察,不能发现有缺陷。为获得更准确的机器视觉测量数据,该实验系统能呈现所有表面缺陷的最大图像尺寸为512×512。再将图像不断缩小,直到所有缺陷都无法辨别,得到最小图像尺寸为20×20。按照SIFT图像金字塔的生成原理,按照1/2不断缩小,从512缩小到20,至少要迭代5次。因此,按照公式(1),a取4,得到金字塔最小组数p为5。
2.2 尺度空间的初始值
尺度空间用来不断地对图像进行高斯模糊,从而达到忽略细节,保留轮廓的目的。高斯模糊参数δ(尺度空间)的计算公式如下:
式中,o为图像所在的组,s为图像所在的层,δ0为初始的尺度,S为每组的层数。对于生活图像的检测和识别应用[7],Lowe给出了以上参数的参考值,取δ0=1.6,S=3。
研究发现,在基于SIFT的工业视觉检测中,δ0的取值非常重要。如果取值太小,则会导致特征点过多,后续计算量过大,影响实时检测的速度。反之如果太大,则会忽略掉图像小的细节,导致特征点过少,影响检测精度。经反复实验发现,δ0的取值可以参考一下经验公式:
式中,k为图像中待检测部分的最小尺寸。在该项目中,瓷砖图像的表面缺陷的最小尺寸约为2像素,因此,δ0取值0.7。
2.3 对比度阈值的确定
确定好金字塔的组数以及尺度空间的参数,就可以得到图像金字塔的尺度空间组,再计算出高斯差分组。
利用尺度空间组的图像,可以找出所有的极值点,查找的原理是以某点为中心,以所在图像及所在组的上下两层图像的3×3区域为邻域,共26点进行比较,如果该点比领域值都大或者都小,则判断为极值点。
以上求得的极值点是在离散图像上获取的,并不一定是真正的极值点。为了找到准确的极值点,我们设从离散极值点到真实极值点的偏差为Δx,用泰勒公式展开可以得到拟合公式(4)。
计算出精确的极值点后,接下来还需要对这些极值点进行过滤。首先是筛选掉低对比度的极值点,同样的,通过设定一个对比度阈值CT来过滤。Lowe给出了CT的建议值是0.04。
在工业检测的应用中,该值的选取也具有一定的灵活性。一般来说,物体轮廓特征点的对比度比纹理等局部特征点要大。因此,如果只想提出物体的轮廓特征来实现识别的目的,则可以将阈值T适当增大,否则可以适当减小,以得到更多局部特征点。
除此之外,还可根据高斯差分空间的高斯核大小来分析CT的取值。对于归一化的图像,如果方差δ0取0.7,则模糊核的中心最大值约为0.32,因此,可以估计出高斯差分图像DOG的最大差值在0.32左右。若保留70%以上对比度的关键点,则可以设CT为0.2.
2.4 图像边框极值点阈值确定
剔除完低对比度极值点后,接下来的工作是筛选掉多余的图像边框极值点。SIFT在计算图像极值点时,很容易将边框点包括在内。一来这些点并不表示图像内容的任何信息,二来如果保留过多边框点,也会严重影响计算速度,所以要尽可能过滤掉。
剔除的原理是通过求极值点水平方向x和垂直方向y的梯度变化比值ET来衡量,如果梯度变化过大,则可以认定是边框点,予以剔除。否则,则认为不是边框点,保留下来。
Lowe给出了ET的建议值是10,在工业实际检测中,为了得到更快的检测速度,要尽可能减小该阈值,以减少边框极值点。但该值减少得太多,又会导致误判其他非边框极值点而剔除。应该根据图像特征区域和边框梯度的变化范围来合理确定阈值。在瓷砖的表面缺陷检测中,ET设置为3是最合适的。
3 实验
经过上述分析和设置,SIFT算法完成了最主要的工作,在图像上找出了经过优化和筛选的极值点,这些留下来的极值点作为最终缺陷识别的特征点。
实验系统的主要环境配置为:操作系统Ubuntu18.4,编译器为Python6.5,图像处理软件为OpenCV3.4,GPU图像处理加速器为GeForce-GTX-1060。
实验用的图像为带碎石和手印干扰的瓷砖缺陷照片,过程包括两个环节,分别是缺陷检出率对比验证,和缺陷误检率对比验证。对比的检测算法包括3种,分别是论文中提到的传统基于图案颜色统计算法MatchTemplate、基于SIFT算子算法和基于卷积神经网络的TensorFlow-CNN深度学习算法[2]。
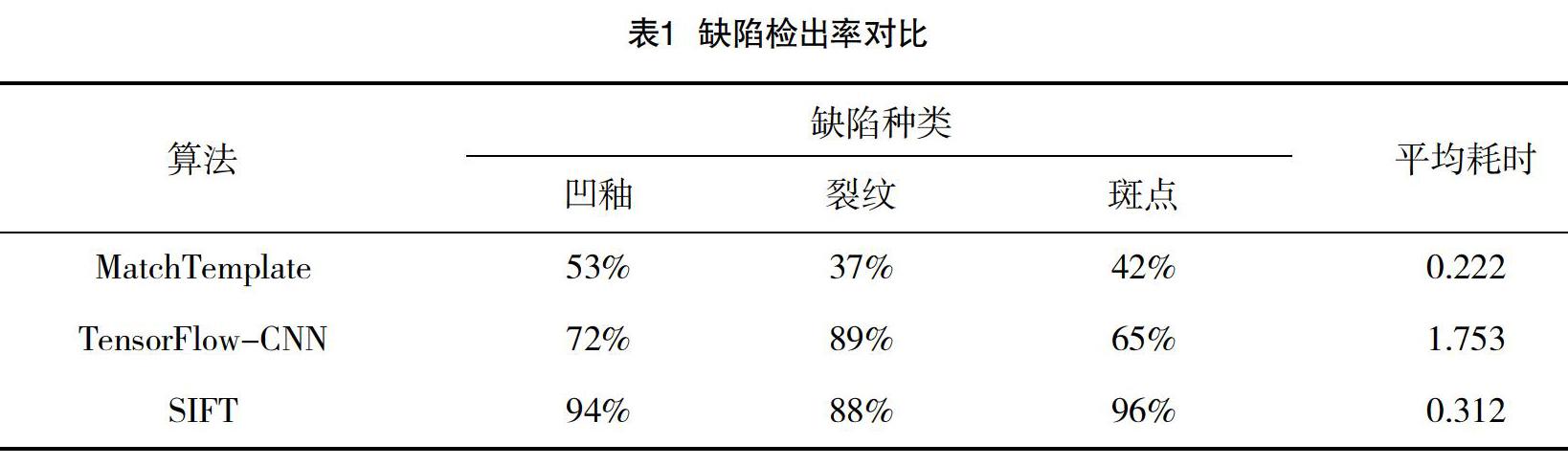
表1列出了3种算法的检出率和平均耗时对比。可以看出,纯粹的图案对比方法MatchTemplate对3种缺陷的检测效果都不佳,主要原因在于缺陷图像的形态变化较大,缩放、旋转、不同区域的亮度变化等,都很容易导致图案匹配算法MatchTemplate失败。而SIFT算法充分考虑了环境因素的变化,因此具有良好的抗干扰能力。TensorFlow-CNN在裂纹识别上具有一定的优势,而在凹釉和斑点的缺陷检测上检出率不高,究其原因是受到碎石和污渍等干扰因素的影响,它们的图像和斑点、凹釉图像类似,和裂纹差距较大。
表2列出了3种算法的误检率和平均耗时对比。MatchTemplate对模板图案高度依赖,因此其误检率和检出率一样不高。TensorFlow-CNN具有一定的适应变化能力,但其对图像的缩放、光照变化等综合影响因素适应能力,以及对碎石、污渍等干扰因素的区分能力并不强,导致其误检率也偏高。而SIFT算法利用的信息较多,充分考虑了环境因素的变化,因此其误检率也较低。
另外,从检测时间上来看,图案比较MatchTemplate算法的原理简单、计算量较小,速度最快,耗时最短。而基于深度学习的TensorFlow-CNN算法结构复杂,神经网络训练和使用过程计算量巨大,耗时长,不太适合工业实时控制要求。而SIFT算法耗时仅比图案比较算法略长,实际应用时,能达到每秒3块瓷砖的检测速度,完全可以满足一般生产线的要求。
4 结论
该文阐述了SIFT算法用于缺陷检测的基本原理,并提出了自适应分数阶微分的改进算法。
(1)SIFT算法的关键是通过图像特征点及其邻域信息来描述特定图案,分数阶微分可显著提高平滑区域特征点的提取,提高缺陷识别率。
(2)通过减少SIFT特征点数量,可以显著减少计算量,提高处理速度。而通过优化SIFT算法的相关参数,图像金字塔组数、尺度空间大小、对比度阈值和边框极值点阈值,可以实现SIFT检测速度和检测精度的平衡。
(3)相对于传统算法和人工智能算法,改进SIFT算法有更高的检测精度和更快的检测速度。
参考文献
[1] 马美荣,李东喜.基于RetinaNet的手机主板缺陷检测研究[J].计算机工程与科学,2020,42(4):673-682.
[2] 金昊,康宇哲,齐希阳,等.基于FasterR-CNN的高压电线缺陷检测方法[J].计算机应用,2019,39(S2):97-102.
[3] 赵艳,左保齐.机器视觉在织物疵点检测上的应用研究综述[J].计算机工程与应用,2020,56(2):11-17.
[4] 周鹏,徐科,杨朝霖.基于SIFT的中厚板表面缺陷识别方法[J].清华大学学报:自然科学版,2018,58(10):881-887.
[5] 张俞晴,何宁,魏润辰.基于卷积神经网络融合SIFT特征的人脸表情识别[J].计算机应用与软件,2019,36(11):161-167.
[6] 曾瑞篷.基于机器视觉的汽车保险盒缺陷在线自动检测系统研究[D].南京航空航天大学,2017.
[7] 张桂梅,郭黎娟,熊邦书,等.基于多分辨率和自适应分数阶的ActiveDemons算法[J].计算机研究与发展,2018,55(12):2753-2763.
[8] 向雨晴,楊晓梅.基于分数阶和非局部全变差模型的图像去模糊[J].计算机工程与设计,2018,39(7):2002-2007.
[9] Rabha W. Ibrahim. A new image denoising model utilizing the conformable fractional calculus for multiplicative noise[J]. SN Applied Sciences,2019,2(1):1718-1720.
