基于修剪树的优化聚类中心算法

周小亮,吴东洋,曹 磊,王玉鹏,业 宁

（南京林业大学信息科学技术学院，南京，210037）

聚类分析方法根据相似度将数据聚集到不同的类或簇中，使簇内数据有较高的相似度而簇间数据差异较大.聚类算法大致可分为五类：基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法以及基于模型的方法.其中，基于划分的k⁃means算法［1-4］可较好地识别球形聚类，具有较快的识别速度，但识别精度易受样本输入顺序的影响，算法稳定性差.基于密度聚类的DBSCAN（Density ⁃ Based Spatial Clustering of Applications with Noise）算法［5-8］可识别非球形样本，但受样本离群点影响较大，算法鲁棒性差.

多年来，研究者先后提出大量基于最小生成树的聚类分析算法，并得到了较好的聚类性能.2013年，徐沁和罗斌［9］将数据投影到主成分分析（Principal Component Analysis，PCA）子空间，给出自适应的mean⁃shift算法，并在PCA子空间内将数据向密度大的区域聚集；利用MST（Minimum Spanning Tree）与图联通分量算法找出类别树和类标签，计算数据在原始数据上的密度峰值，并将峰值点作为k⁃means聚类的初始中心点.与k⁃means算法相比，该算法能在较短的时间内给出较优的全局解.2014年，Ye［10］自定义SVNs（Single⁃Valued Neutrosophics）距离测度，并在此基础上提出基于SVM（Support Vector Machine）的广义距离测度的SVNMST（Single⁃Valued Neutrosophic Minimum Spanning Tree）聚类算法，并在实际数据集上取得较好的应用效果，但该算法的聚类精度受SVNs距离测度的影响较大.2014年，徐晨凯和高茂庭［11］提出改进的最小生成树自适应分层聚类算法，根据近邻关系为每个聚类簇设定独立的阈值，适应分布密度相差较大的情况，实验结果表明，在分布密度不均时算法可获得较好的聚类效果.2016年，贾瑞玉和李振［12］将初始样本构造成最小生成树，利用层次分裂思想将树划分成多个簇，通过k⁃means算法迭代操作得到每次操作的评价函数值来判断是否进行簇合并，该算法能够准确地判定聚类的数目.2018年，Jothi et al［13］利于基于质心的近邻规则生成一个稀疏的局部邻域图，利用邻域图构造近似的MST，在综合数据集和真实数据集上的实验表明，在保持近似MST聚类质量的前提下计算时间显著减少.2019年，Li et al［14］提出基于距离尺度MST的不同密度簇间最长边寻找方法，在小数据集和高维数据集上的效果比较理想.2019年，Mishra and Mohanty［15］将数据划分为多个子聚类，为每个子聚类构造最小生成树，合并相邻的子聚类得到最终聚类结果，在真实数据集上的聚类精度显著提高.2019年，李蓟涛和梁永全［16］通过计算数据集密度峰值估算全局密度，将数据集分为高密度区域和低密度区域，构建、分割最小生成树对低密度区域样本进行关联挖掘，最后根据簇的密度对簇进行合并，得到最终的聚类结果.选取多个UCI数据集和不平衡的人工数据集进行测试，验证了该算法的有效性和鲁棒性.2020年，Mishra and Mohanty［17］获取MST邻域信息，通过边权值及离群值检测将数据集划分为若干簇，再根据拓扑不连通性和内部相似度将簇合并，在真实数据集上取得了较好测试性能.

针对传统聚类算法存在的非球形类簇识别困难和较高鲁棒性的问题以及基于最小生成树算法存在的中心点确认困难的问题，本文提出一种新的聚类方法OCT（Optimized Clustering Center Based on Trimmed Tree）.该方法通过构建最小生成树并多次修剪以寻找初始类簇中心，根据样本加权距离确定样本数据的归属，解决了样本形状对聚类精度的影响及噪声样本敏感性的问题.对比实验结果表明，该方法具有较高的聚类精度及较好的识别速度.

1 OCT算法

1.1 最小生成树(MST)

定义1无向图G=(V，E)，V表示顶点，E表示边，(u，v)表示顶点u，v之间的边，w(u，v)表示边的权重，若存在T（E的子集）集合，使w(T)最小，则T为最小生成树，如式（1）所示：

定义2若T为最小生成树，可定义T的权重均值WeightMean，如式（2）所示：

其中，edgei是最小生成树T中第i条边的权重，N为最小生成树T的顶点数.

定义3若T为最小生成树，定义结点间权重误差WeightVar，如式（3）所示：

1.2 修 剪

1.2.1 离群点离群点是指数据集中的噪点或处于类簇边缘的点，最小生成树中可将度为1的叶子结点定义为离群点.

离群点修剪，即修剪叶子结点.离群点修剪可去除数据噪点，得到相对致密的数据簇集.该修剪过程可为构建最小生成树提供趋向度准确的数据集，以解决类簇边缘样本位置较近甚至样本交错导致算法识别性能不高的问题.

1.2.2 修剪枝

定义4对于最小生成树T，裁剪值mstCut定义如式（4）所示：

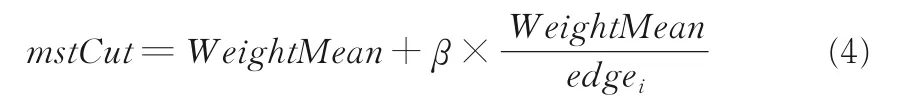
其中，β为调和因子，值越低对权重大的边越敏感，反之则对权重小的边越敏感.可设置β的值如式（5）所示：

由式（4）和式（5）可知，mstCut可根据样本数量以及样本的空间上分布自适应调节裁剪尺寸.

由于five_cluster和fourty数据集的密度不均匀，孤立样本点较多，这两个数据集上被修剪边的数量随着Q值的改变呈线性增加，所以选择合适Q值可以在不影响其他数据集的情况下剔除噪点样本.经过多次实验（实验结果如图1所示），当Q值设定为1.5时，可以有效地剔除数据集中的孤立样本，还不会改变数据簇集的初始形态.

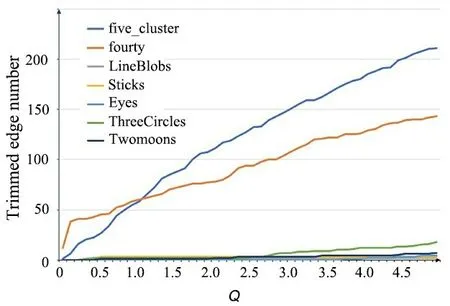
图1 修剪边数量与Q 的关系Fig.1 Relationship between trimmed edge number and Q

1.3 质心偏度

1.3.1 质心偏量

定义5获取k个类的初始样本点，设Oi(xi，yi)为初始聚类质心.

其中，ε为第i(i≤k)个类的初始样本个数，(xj，yj)为第i个类中第j个样本的点坐标位置.

定义6将待测样本点C(x，y)加入类中，则在初始类的样本数据基础上更新类质心为，如式（8）和式（9）所示：

由式（6）和式（7）可得样本点加入类簇后的质心偏量GravityOffset，如式（10）所示：

1.3.2 样本偏量

定义7从初始类内样本集中选取与待测样本点C(x，y)距离最近的n个样本，计算n+1个样本点的质心如式（11）和式（12）所示：

其中，n为样本特征维度.

定义8在式（11）和式（12）基础上可定义样本偏移SampleOffset，如式（13）所示：

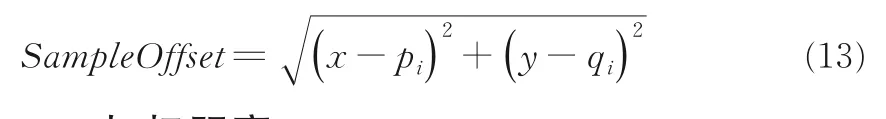
1.3.3 加权距离

定义9将质心偏量、样本点偏量（欧式距离）作为距离尺度，可以给样本点分类，样本加权距离为SampleDistancei，如式（14）所示：

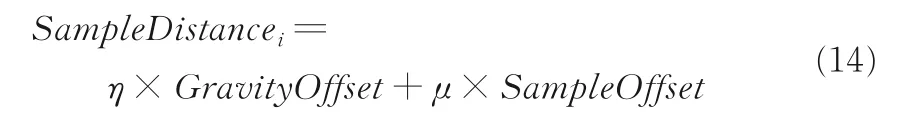
其中，η为质心偏量权值，μ为样本偏量权值.

定义10定义平均初始聚类簇中心距离Dis-Gravity如式（15）和式（16）所示：

其中，distanceij是第i个聚类簇的中心到第j个聚类簇的中心的距离.

对数据多次分析并结合式（2）和式（16），可得参数η和μ的取值范围如式（17）和式（18）所示：

在LineBlobs数据集中，η和μ的取值与识别率的关系如图2所示.由图可见，当识别率达到100%时（图中的红色粗线），μ的取值明显高于η的取值，这是由于该数据集在空间上的分布为非球形簇，具有较密集的初始聚类簇质心.随着η的取值上升，μ的取值下降，识别率逐渐降低.

图3所示为在five_cluster数据集中η和μ的取值与识别率的关系.由图可知，当识别率达到最高99.6%时（图中的绿色粗线），η的取值明显高于μ的取值，这是由于five_cluster数据集的空间分布为球形簇，初始聚类簇质心较为分散.随着μ的取值上升，η的取值下降，识别率逐渐降低.

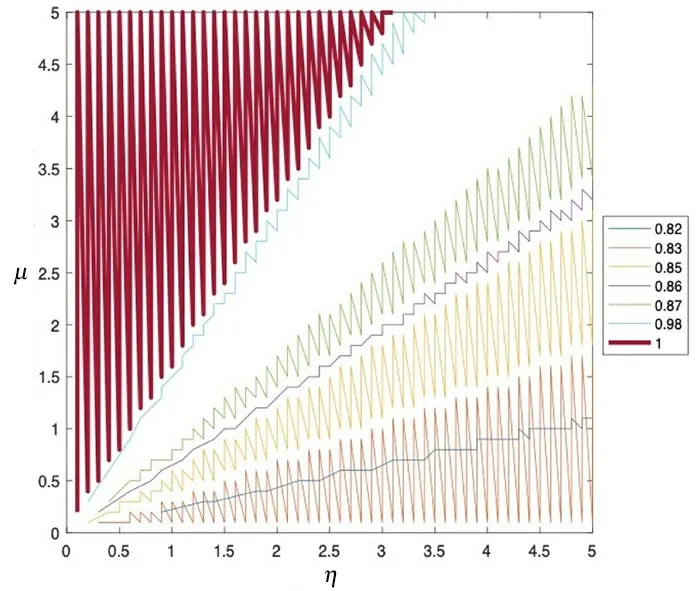
图2 LineBlobs数据集中η和μ 与识别率的关系Fig.2 The relationship between η，μ and recognition on the LineBlobs dataset

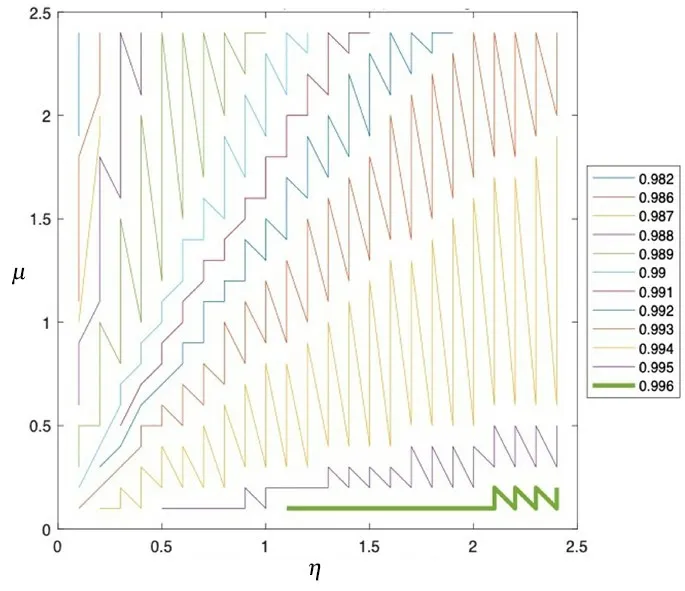
图3 five_cluster数据集中η和μ 与识别率的关系Fig.3 The relationship between η，μ and recognition on the five_cluster dataset

1.4 算法流程

2 实验结果与分析

2.1 人工数据选取七种在空间上呈单一或混合形状的二维人工数据集，数据集信息如表1所示.five_cluster数据集包含五个类簇，每个类簇呈致密球形，簇的周边存在少量噪点，其中两个相邻簇间存在交叉样本.fourty数据集包含40个类簇，每个类簇有25个样本，簇集数量较多.Line⁃Blobs，Sticks，Eyes，ThreeCircles，Twomoons数据集包含流线形、环形、月牙形以及多种形状的混合，类簇间距离不均，每个类簇内部存在样本分布密度不均现象.

表1 实验使用的人工数据集的信息Table 1 The information of manual datasets

本文的实验平台均采用Inter Core i5处理器3.1 GHz，8G内存，MacOS 10.15.4，算法实现采用Matlab 2017b.

为验证OCT算法的有效性，分别使用OCT，k⁃means，DBSCAN算法对上述人工数据集进行聚类分析，并对比其识别精度及识别速度，聚类结果如图4至图10所示.

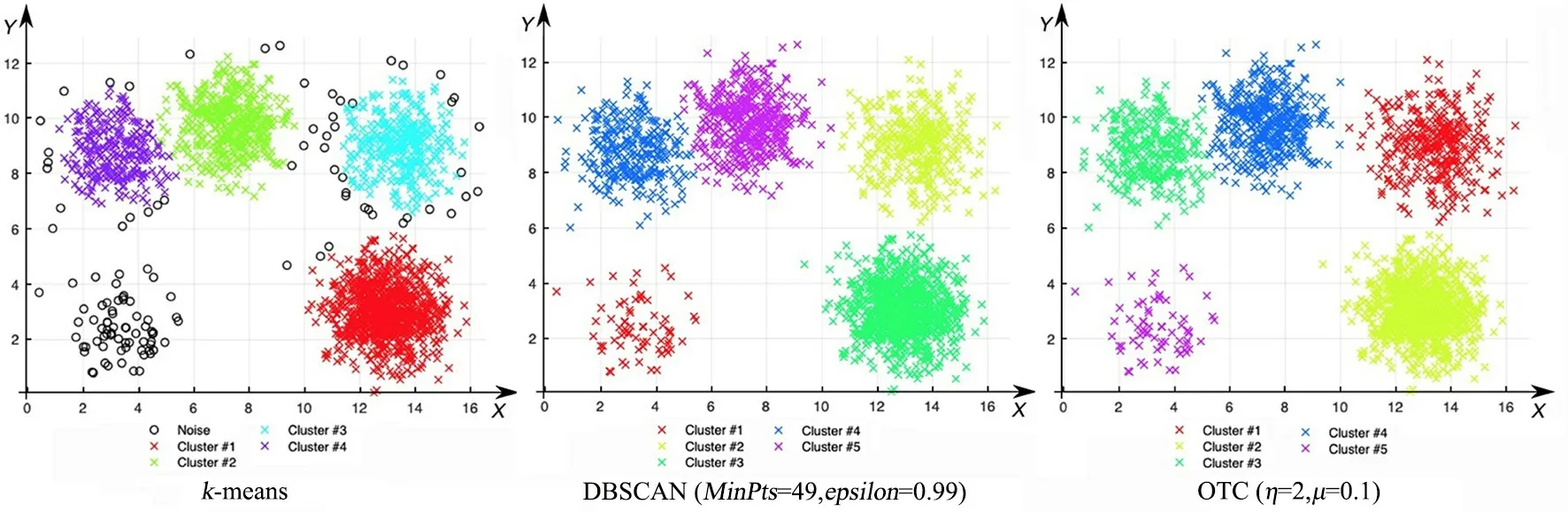
图4 k-means，DBSCAN和OCT算法在five_cluster数据集上的聚类结果Fig.4 The clustering results of k-means，DBSCAN and OCT on five_cluster dataset

图5 k-means,DBSCAN和OCT算法在fourty数据集上的聚类结果Fig.5 The clustering results of k-means,DBSCAN and OCT on fourty dataset

第一组，five_cluster数据集（图4）包含五类数据，每一类样本的周边都存在孤立点，导致DB⁃SCAN聚出的结果存在许多噪点.由于这五类数据集在空间分布上呈球形簇，所以k⁃means聚类效果较好；而OCT算法通过聚类中心及初始边界来划分聚簇，存在少量样本未被准确划分的现象，聚类精度为99.6%.在fourty数据集（图5）中，由于k⁃means算法随机选取聚类中心，导致部分样本聚集错误，而OCT算法的聚类结果明显优于k⁃means和DBSCAN，准确度达100%.对Line⁃Blobs数据集（图6），k⁃means聚类将下半部分圆弧形样本划分为三个簇集，而OCT和DBSCAN均能获得准确的聚簇划分，聚类精度为100%.Sticks（图7），ThreeCircles（图9），Twomoons（图10）数据集在空间上呈现非球形簇，k⁃means的识别效果较差，识别精度仅为63.44%～73.37%；而DBSCAN与OCT算法在类间区分明显且在类内分布均衡的数据集上均有较好的识别效果，识别率均达100%.OCT算法在Eyes（图8）数据集上的识别精度为92.01%，和k⁃means和DB⁃SCAN算法相比，识别精度提升明显.由于Eyes数据集中存在分散环状外围数据，且该环状数据与中间两类簇存在密度接近的区域，故而导致DBSCAN的识别结果存在较多噪点，识别率仅为78.15%.综上，OCT算法在人工数据集上的聚类精度明显优于k⁃means和DBSCAN算法.

图6 k-means,DBSCAN和OCT算法在LineBlobs数据集上的聚类结果Fig.6 The clustering results of k-means,DBSCAN and OCT on LineBlobs dataset

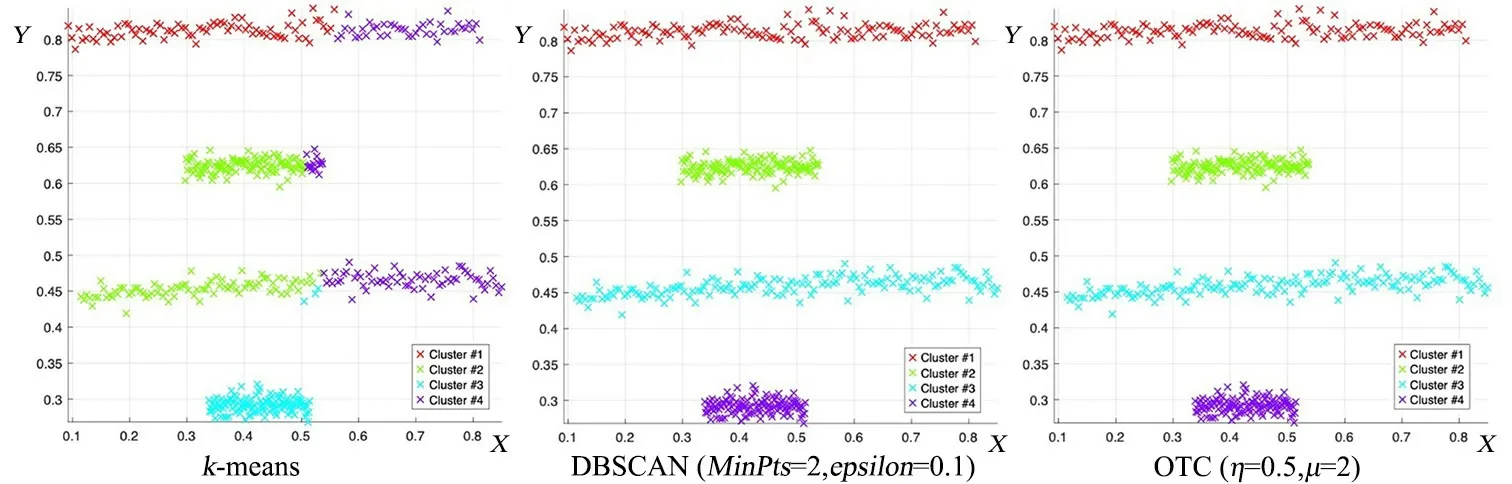
图7 k-means,DBSCAN和OCT算法在Sticks数据集上的聚类结果Fig.7 The clustering results of k-means,DBSCAN and OCT on Sticks dataset

图8 k-means,DBSCAN和OCT算法在Eyes数据集上的聚类结果Fig.8 The clustering results of k-means,DBSCAN and OCT on Eyes dataset

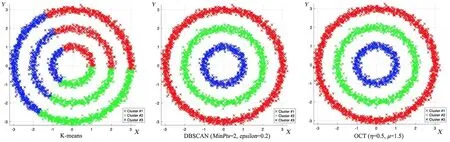
图9 k-means,DBSCAN和OCT算法在ThreeCircles数据集上的聚类结果Fig.9 The clustering results of k-means,DBSCAN and OCT on ThreeCircles dataset

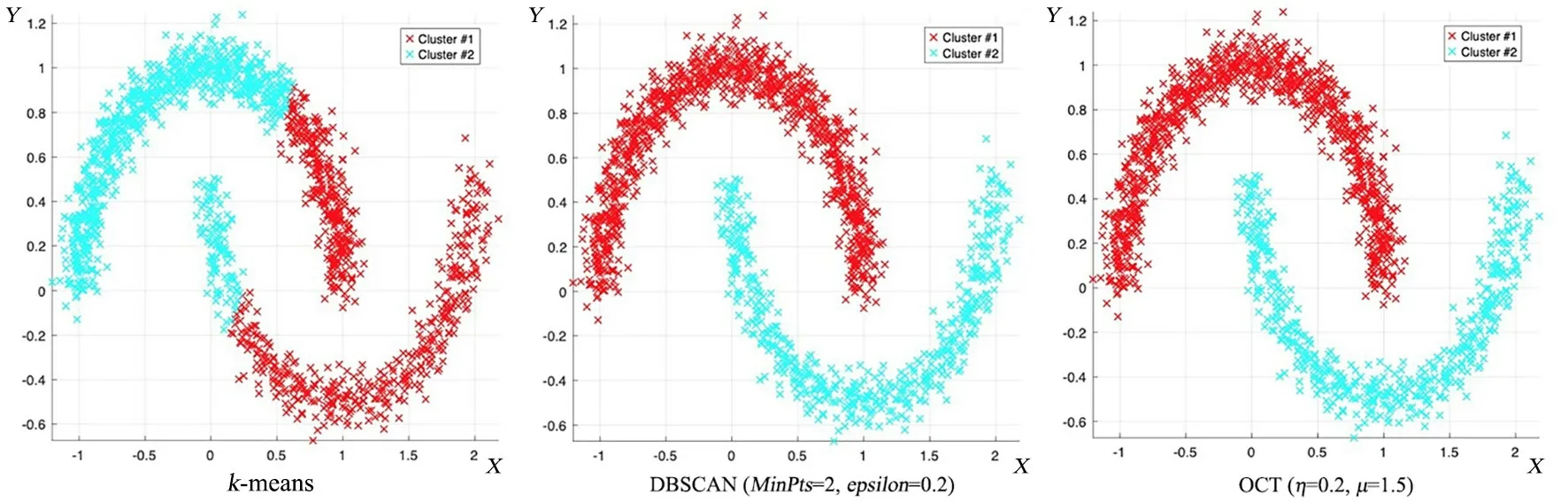
图10 k-means,DBSCAN和OCT算法在Twomoons数据集上的聚类结果Fig.10 The clustering results of k-means,DBSCAN and OCT on Twomoons dataset

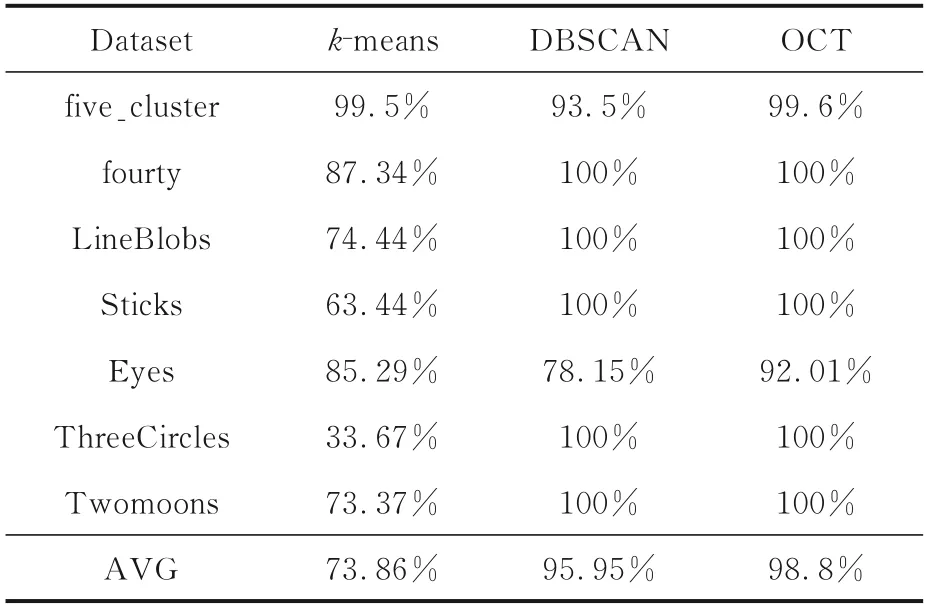
表2 k-means,DBSCAN和OCT算法在人工数据集上的聚类精度对比Table 2 The clustering accuracy of k-means,DBSCAN and OCT on manual datasets

由对比结果（表2）可知，OCT算法的平均聚类精度为98.8%，优于其他两种算法；同时，OCT可满足任意形状类簇，且聚类效果不受噪点的影响.进一步分析OCT算法对Eyes数据集聚类效果仅为92.01%的原因，发现Eyes数据集中环形簇的样本点分布较为分散，导致修剪最小生成树所得的初始聚类簇存在较大偏差.DBSCAN算法的聚类性能次之，但对不均衡的five_cluster和Eyes数据集，该算法会存在较多噪点.

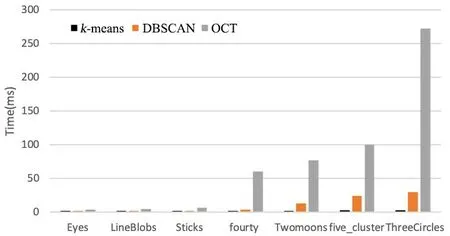
图11 k-means,DBSCAN和OCT算法在人工数据集上的聚类时间比较Fig.11 The clustering time of k-means,DBSCAN and OCT on manual datasets

分别统计三种聚类算法在七个人工数据集上的聚类时间，结果如图11所示.k⁃means算法的聚类速度最快，平均消时0.113 ms；DBSCAN算法次之，平均耗时7.06 ms；而OCT算法平均耗时57 ms.其中，OCT算法在Eyes和LineBlobs数据集上花费的时间与k⁃means和DBSCAN相比差距不大，但在ThreeCircles数据集上消耗的时间最长，达到272.57 ms.这是由于ThreeCircles数据集包含3603个样本，且OCT算法在运行过程中需要多次构建和修剪最小生成树，因而花费了大量的时间.进一步做算法分析可知，k⁃means算法的时间复杂度为O(n)；DBSCAN算法的时间复杂度为O(n×θ)（θ为邻域内找点的时间花费），最坏的情况下时间复杂度为O(n2)；OCT算法的时间复杂度为O(n2).

2.2 真实数据为检验OCT算法在实际数据集上的聚类性能，使用UCI数据库的leaf数据集和人工收集植物叶片数据的并集作为测试样本集，共包含48种871张植物叶片图像样本.其中，leaf数据集包含40种植物，每种植物含8～16张数量不等的二值叶片图像；人工收集的数据集包含八种自然环境下的植物叶片，经过数据预处理得到每组含30～40张数量不等的叶片二值图像.

从上述真实数据集中随机选取多组样本图像，每组样本包含三种10～30张具有代表性的植物叶片图像.每组样本选取其中一幅二值图像，如图12所示.四组样本信息如表3所示.BBQ数据集中的叶片为竹叶（Bambusoideae）、构树（B.papyrifera）、夏栎（Q.robur）；QUG数据集中的叶片为夏栎（Q.robur）、荨麻（U.dioica）、天竺葵（G.sp）；GQN数据集中的叶片为银杏叶（Ginkgobiloba）、夏栎（Q.robur）、竹叶（Bambusoideae）；BQG数据集中的叶片为竹叶（Bambusoideae）、夏栎（Q.robur）、天竺葵（G.sp）.原始图像分别经过预处理、形状特征提取、归一化、降维等过程，得到图像特征集，该特征数据集将作为聚类分析的样本数据集.

图12 测试实验中使用的叶片数据集Fig.12 Leaf datasets used in the test experiments

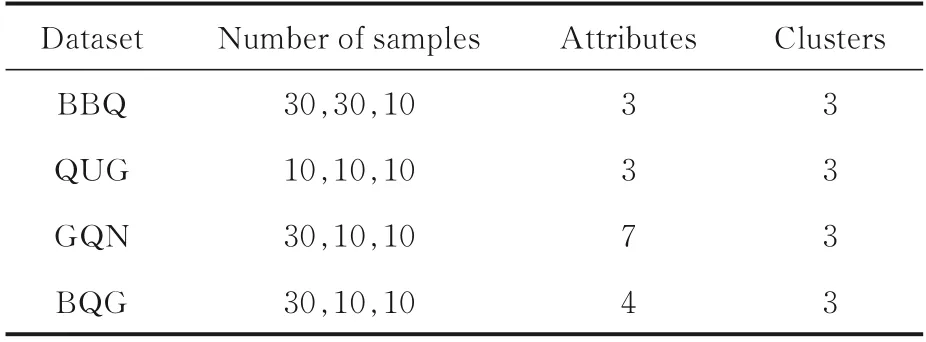
表3 植物叶片数据集Table 3 Plant leaf datasets

k⁃means，DBSCAN，OCT三种算法在四种叶片数据集上的聚类精度如表4所示.由表可见，OCT算法的平均聚类精度为95.7%，明显高于k⁃means和DBSCAN.在BBQ和BQG数据集上三种算法的聚类精度均未达到100%，这可能是受叶片图像狭长度（N）、形状参数（F）的影响，样本点在空间分布上呈交错状态.但即使如此，OCT的聚类精度仍达90% 和92.8%，明显高于k⁃means和DBSCAN.在QUG和GQN数据集上，OTC的聚类效果较好，均为100%.DBSCAN在QUG数据集上的聚类精度也为100%，而在GQN数据集上的聚类精度为96%，略低于OCT.k⁃means算法在GQN数据集上的聚类精度远低于另外两种算法，可能是由于GQN数据集的维度较高，数据在空间上的分布呈不规则球形簇.

三种算法在四个叶片数据集上的聚类时间如图13所示.经计算，OCT算法耗时最长，平均耗时10.53 ms；DBSCAN算法次之，为3.974 ms；而k⁃means算法耗时最短，为2.834 ms.OCT在QUG，GQN和BQG上消耗的时间较长，主要是因为在构建最小生成树的阶段，时间复杂度较高；而在BBQ数据集上耗时最长的主要原因是BBQ数据集的样本量最多.

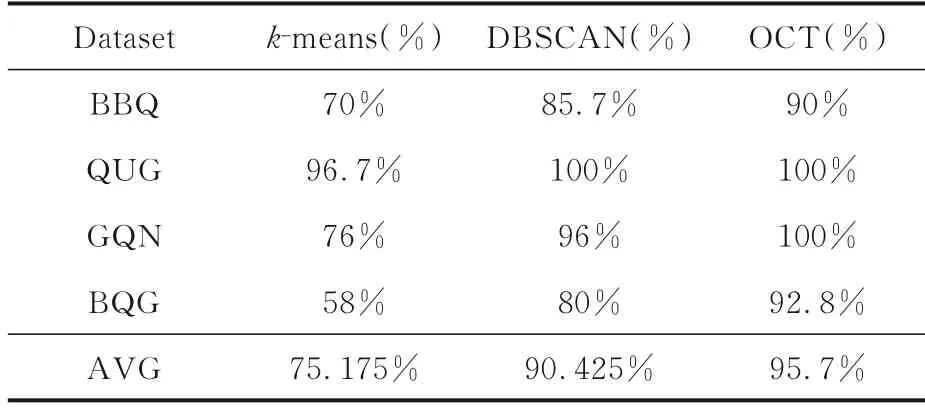
表4 k-means,DBSCAN和OCT算法在四种叶片数据集上的聚类精度比较Table 4 The clustering accuracy of k-means,DBSCAN and OCT on four leaf datasets

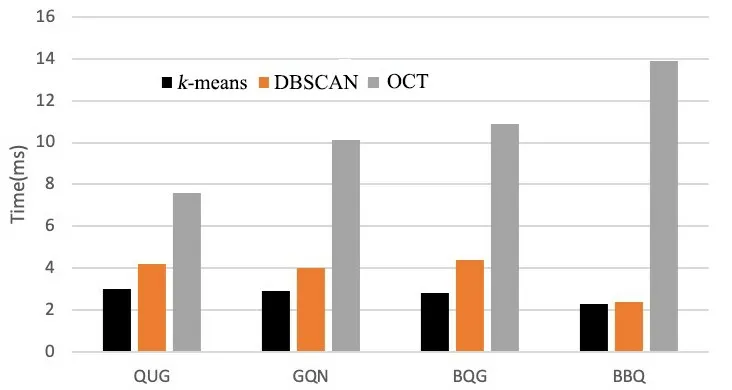
图13 k-means,DBSCAN和OCT算法在四种叶片数据集上的聚类时间对比Fig.13 The clustering time of k-means,DBSCAN and OCT on four leaf datasets

3 结论

本文提出一种基于修剪树的优化聚类中心算法OCT，可以有效地解决样本数据密度不均衡以及存在大量孤立噪点等问题.OCT算法通过修剪最小生成树并获取与叶子相邻结点的质心作为初始聚类中心，可以有效地剔除样本中噪点对聚类结果的干扰；对质心偏量以及样本偏量设置不同的参数，还可以识别空间上的任意形状簇.在人工数据集和真实数据集上的对比实验都证明该算法的准确度较高.

由于OCT算法在执行过程中需要多次构建最小生成树，时间花费较长，在样本数量相同的情况下，虽然聚类精度高于k⁃means和DBSCAN两种算法，但耗时更长，说明样本量对该算法的时间影响较大，计算的时间复杂度高.为进一步解决算法的时间复杂度问题，提升算法速度，可尝试新的建树策略，如使用邻阈图构造近似的最小生成树来降低构造最小生成树的时间复杂度.