Investigation of Numerical Conditions of Moving Particle Semi‑implicit for Two‑Dimensional Wedge Slamming

Takahito Iida · Yudai Yokoyama

Abstract The sensitivity of moving particle semi-implicit (MPS) simulations to numerical parameters is investigated in this study.Although the verification and validation (V&V) are important to ensure accurate numerical results, the MPS has poor performance in convergences with a time step size. Therefore, users of the MPS need to tune numerical parameters to fit results into benchmarks. However, such tuning parameters are not always valid for other simulations. We propose a practical numerical condition for the MPS simulation of a two-dimensional wedge slamming problem (i.e., an MPS-slamming condition). The MPS-slamming condition is represented by an MPS-slamming number, which provides the optimum time step size once the MPS-slamming number, slamming velocity, deadrise angle of the wedge, and particle size are decided. The simulation study shows that the MPS results can be characterized by the proposed MPS-slamming condition, and the use of the same MPS-slamming number provides a similar flow.

Keywords Wedge slamming · Moving particle semi-implicit · MPS-slamming condition · Numerical condition · Wagner’s theory · Computational fluid dynamics

1 Introduction

Computational fluid dynamics (CFD) has been developed and widely used for the last few decades. Recently,CFD solvers have been used to unravel natural phenomena whose behaviors are not modeled by the conventional physical model (i.e., strongly nonlinear phenomena). Industrial fields have also used CFD software for the analysis of their products. As for the wave dynamics field in the naval architecture, the CFD is often used to simulate an unsteady ship motion (e.g., Waskito et al. 2020) and slamming of a ship (e.g., Judge et al. 2020). Because the estimations of hydrodynamic forces are important for designing ships, the accurate estimation of these forces is highly demanded in academic and industrial societies.

Among these ship-related phenomena, the hull slamming,that is, the entry of a ship body onto the water surface, is of great concern because of impulsive loads with high pressure on local components and induced global vibration of the body. The slamming problem is a strongly nonlinear phenomenon consisting of the nonlinearity of free surface conditions, splash of water, and involution of air and water.To understand slamming problems, mathematical solutions were developed in consideration of the following physical models: linear model using an equivalent plate (Wagner 1932), nonlinear-free surface condition (Dobrovol’Skaya 1969; Wang and Faltinsen 2017), splash of water (Watanabe 1986; Cointe and Armand 1987), higher-order term of the Bernoulli equation (Korobkin 2004), sea depth effect(Jalalisendi et al. 2017), and hydroelasticity of the body(Faltinsen 1999; Khabakhpasheva and Korobkin 2013). In addition, experiments on wedge slamming with constant speed (e.g., Chuang 1967; Tveitnes et al. 2008; Allen 2013;Jain et al. 2020) and free-falling slamming (e.g., Yettou et al. 2006; Panciroli and Porfiri 2013; Vincent et al. 2018)were performed. These analytical and experimental studies have greatly contributed to unraveling the slamming phenomena. However, the approaches used are generally applied to simple cases. To consider the arbitrary shape of objects and multiple physical models, the development of numerical approaches has been demanded. Numerical solutions were first studied using the boundary element method(BEM) based on the potential flow (Zhao and Faltinsen 1993; Kihara 2004; Sun and Faltinsen 2007). Furthermore,CFD approaches have been developed to directly solve the Navier–Stokes equations. Multiphase Navier–Stokes equations around a wedge were solved by the constrained interpolation profile scheme (Tajima and Yabe 1999). The volume of fluid-based OpenFOAM was used for simulating the slamming of flexible wedges (Maki et al. 2011; Piro and Maki 2013). Free-falling slamming was validated using the open-source CFD model REEF3D (Kamath et al. 2017).Rigid wedge slamming was simulated by smoothed-particle hydrodynamics (SPH) (Oger et al. 2006). SPH was coupled with a finite element method (FEM) for solving the slamming of a flexible body (Fourey et al. 2017; Hermange et al.2019). Although the FEM is a major approach for analyzing structure dynamics, some fluid analyses were coupled with particle-based structure simulation methods. SPH–SPH(Oger et al. 2009) and incompressible SPH (ISPH)–SPH(Khayyer et al. 2018a) simulations were demonstrated. The moving particle semi-implicit (MPS) method was also used for fluid–structure interaction (FSI) problems with the coupling with a Newtonian structure MPS or a Hamiltonian MPS (Khayyer et al. 2018b).

Among several CFD approaches, particle-based simulation methods (i.e., SPH and MPS) are expected as suitable schemes for simulating slamming problems (Seddon and Moatamedi 2006) due to their mesh-free and Lagrangian characteristics. These characteristics enable us to easily simulate water splashes caused by the slamming and large deformation of a free surface and a flexible body. Moreover, particle-based simulation methods might be suitable to solve complicated phenomena, such as slamming with an ice floe (Yokoyama and Iida 2021). In this study, we focus on the MPS method for the simulation tool of the slamming problem. The MPS is widely used for simulations of the free surface flow. Several enhanced schemes have been proposed from various aspects: pressure gradient (Iribe and Nakaza 2011; Khayyer and Gotoh 2011), source term of a pressure Poisson equation (PPE) (Khayyer and Gotoh 2009; Tanaka and Masunaga 2010; Khayyer and Gotoh 2011), boundary conditions (Marrone et al. 2010; Tsuruta et al. 2015; Duan et al. 2021), particle regularization (Tsuruta et al. 2013),time marching method (Matsunaga and Koshizuka 2021),multiphase flow (Khayyer and Gotoh 2016; Wang and Zhang 2019), and FSI coupling (Hwang et al. 2016; Khayyer et al.2019). These schemes have improved the reliability of MPS simulations.

In general, using the CFD is easier than using conventional physical-based simulation models. Furthermore, the results of the CFD are sensitive to the numerical and tuning parameters (e.g., time step size, mesh/particle size, and stabilized parameters), and the accuracy of results depends on these settings. Therefore, CFD users need appropriate knowledge and know-how to obtain robust simulation results. To overcome the uncertainty of errors due to the modeling and tuning parameters, verification and validation analysis is a primary necessity (Oberkampf and Trucano 2002). However, the MPS does not show a good convergence with respect to the numerical parameters (Matsunaga and Koshizuka 2021) because results do not converge to a definitive value even if the numerical parameter becomes smaller.This fact yields difficulties in the verification of MPS simulations. As a result, MPS users have no choice but to tune numerical conditions for obtaining good results.

In this study, we investigated the sensitivity of simulation results to numerical parameters using the MPS method.We also attempted to make a practical numerical condition for an MPS simulation of a slamming problem, namely, an MPS-slamming condition, which provides us with suitable numerical parameters. Because the MPS has poor convergence with numerical parameters, the MPS-slamming condition could not be made by only using a numerical context; it may need knowledge based on a physical model. Based on this condition, an MPS-slamming condition was made using numerical and physical conditions. Because of its wide use in many studies, the two-dimensional (2D) wedge slamming problem was considered here. In particular, the Wagner solution (Wagner 1932) was referred to characterize a flow around the wedge slamming and make an MPS-slamming condition that connects physical and numerical parameters using a defined MPS-slamming number. An MPS solver was developed on the basis of tuning-less schemes (e.g., Marrone et al. 2010; Khayyer and Gotoh 2011). The results were compared with the simulation results using OpenFOAM(Chen et al. 2019). The sensitivity of the MPS simulation to numerical and physical parameters was investigated using the proposed MPS-slamming condition. The results show that the MPS results can be characterized using the MPSslamming condition, and a similar flow can be obtained using the same MPS-slamming number. This finding indicates that the optimum time step size can be provided once the MPS-slamming number, slamming velocity, deadrise angle of the wedge, and particle size are decided.

2 Theory of Particle‑Based Simulations

2.1 Particle Interaction Model

In this study, the particle-based simulation method was developed based on the MPS (Koshizuka and Oka 1996).Fluid was discretized as a number of particles, and the densities were estimated by the weighted interaction with neighboring particles. The particle number densityniis defined as follows:

wherew(r) is the kernel function andrijis a distance between particlesiandj. The Wendland kernel (Wendland 1995;Ikari et al. 2015) is used for the kernel function as follows:

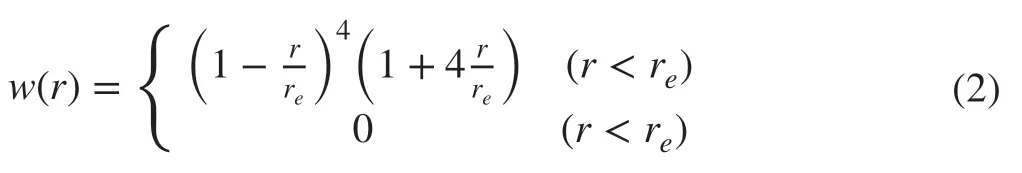
wherereis a radius of influence. The derivative and second derivative of the Wendland kernel are continuous atr=re.

2.2 Fluid Simulation Model

Recently, several enhanced MPS schemes have become available. However, some of them need tuning parameters and relaxation coefficients, such as free surface condition (Koshizuka and Oka 1996) and source term of a PPE(Tanaka and Masunaga 2010), although these schemes are widely used (e.g., Duan et al. 2021). These schemes dramatically stabilize results, but parameter studies are required, and resultant parameters are not always valid for other problems. The present MPS solver is developed based on tuning-less schemes (e.g., Marrone et al. 2010;Khayyer and Gotoh 2011) that eliminate arbitrary tuning parameters as able as possible. Fluid dynamics is governed by the continuity equation and Navier–Stokes equations as follows:

whereρis the fluid density,uis the velocity vector,Pis the pressure,νis the kinematic viscosity, andgis the gravitational acceleration. We considered the 2D incompressible flow with the verticalx−yplane where they-axis is positive vertically upward. The projection method was applied to guarantee the incompressibility of fluid, and a resultant equation became the PPE as follows:

The ECS corrects the numerical error without an arbitrary tuning of relaxation coefficients. For the computation of the left-hand side of (5), the higher-order Laplacian (Khayyer and Gotoh 2010) is applied as follows:

Once the pressure field was obtained, the mid-time step velocity field was corrected to the true velocity field as follows:

l0is an initial distance of particles (particle size). The pressure gradient is described by the higher-order gradient (HG)(Iribe and Nakaza 2011), also known as the gradient correction (GC) (Khayyer and Gotoh 2011), which is based on the first-order Taylor series expansion, as follows:

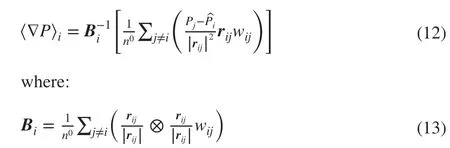
Here,̂Piis the minimum pressure among the particleiand its neighboring particles. The matrixBisometimes does not have an inverse matrix. To prevent failure of the calculation,a zeroth-order gradient model (original gradient model) was employed when the determinant ||Bi||<εHGis satisfied or the number of neighboring particles is less than a thresholdNHG.

2.3 Free Surface Detection

In the MPS, a free surface condition is satisfied by imposing zero pressure on free surface particles. The original free surface detection uses a tunable threshold, and erroneous detections frequently happen. To ensure the robustness of the free surface detection without any tuning parameter, we utilized the combination of two schemes from geometrical and temporal viewpoints instead of the original one.

The first scheme is parachute detection (Marrone et al.2010). Particles are identified as free surface particles if any neighboring particle does not exist in the following scanning areas (parachute area composed ofA1andA2):

This scheme judges free surfaces based on the geometrical arrangement of particles. However, this method cannot prevent all births of non-physical free surface particles inside the fluid if geometrical rarefaction is caused by a violent flow. To avoid this irregularity, we imposed an auxiliary condition, namely, the free surface assessment by time tracing of free surface particles (FATT), on the basis of the temporal tracing of the free surface. Particles should satisfy the following criterion to be treated as a free surface:

is a flag that judges whether a particleiis a free surface particle at timek. This condition indicates that the particleican be supplementarily identified as a free surface particle only if at least one particle, which is the free surface particle at the previous timek−1, is existing within the effective radius of the particlei. In other words, this criterion implies that the free surface does not suddenly occur inside the fluid. This scheme suppresses the birth of non-physical free surface particles inside the fluid regardless of the geometrical rarefaction. Note that this assessment can be used when cavitation is not considered.

2.4 Wagner’s Theory

Wagner’s theory (Wagner 1932) is briefly reviewed here and described in detail in Faltinsen (1993). We consider the 2D water entry problem of the wedge with the constant speedV. The origin of the coordinate system (x,y) is placed at the undisturbed free surface, and they-axis is positive vertically upward. The incompressible and inviscid flow with irrotational motion is assumed to be treated as the potential flow.According to Wagner’s theory, the wedge is replaced by a flat plate on the free surface. The half-width of the platecis equivalent to the wetted half-width of the wedge; that is, the half-widthcis variable with respect to timet. Focusing on a time instant, the boundary value problem can be formulated as follows:

where Φ is the velocity potential, [L] is the Laplace equation, [F] is the simplified free surface condition, and [H] is the body boundary condition. Here, the water depth is deep enough. The free surface elevationη(x) is then expressed as follows:

The geometry of this problem gives the following condition:

However, (23) has a singularity at point |x|=c, and the maximum pressure diverges to infinity due to the physically inconsistent boundary condition. In fact, the jet flow is found in the vicinity of this point, and the pressure is almost constant and close to atmospheric pressure. According to Wagner’s theory, the maximum pressure coefficient is replaced to:

where πρc2∕2 is the added mass (in vertical motion) of the flat plate for an infinite natural frequency.

2.5 MPS‑Slamming Condition

In this section, we discuss the numerical condition of the MPS method. Because the CFD is based on the discrete system, finite sizes of the time step Δtand mesh Δx(or particle sizel0) should be used. In the simulations of the discrete system, the Courant condition (or Courant Friedrichs Lewy condition) is imposed asCCFL≥umaxΔt∕Δx, whereumaxis the maximum velocity of the fluid. The Courant condition is a necessary condition in the numerical simulation that restricts fluid movements at a one-time step to be less than the mesh size. In the MPS, the mesh size is replaced to the particle sizel0, andCCFL=0.2 is often recommended for obtaining stable results (Koshizuka and Oka 1996). This condition provides the guideline of the coarsest mesh condition. Generally, the results of the CFD converge to a definitive value as time step size becomes smaller. However, the typical MPS simulation does not show such a convergence(Matsunaga and Koshizuka 2021), and the use of a small time step size does not indicate a better simulation result.As a result, MPS users need to search the numerical conditions using trial and error. In other words, the results of the MPS might be tuned to fit the referred data using arbitrary numerical parameters (e.g., relaxation coefficients).

To obtain reliable simulation results, deliberate tuning must be removed. Accordingly, we investigated the sensitivity of MPS simulation results to numerical parameters(particularly the time step size) and proposed a practical numerical condition. Because the MPS suffers from a poor convergence with numerical parameters, the numerical condition could not be made only by the numerical context.Therefore, the knowledge of the physical model was integrated to make the practical numerical condition. According to Wagner’s theory presented in Sect. 3, the flow around the wedge slamming can be characterized by the slamming velocityVand deadrise angleβ, as denoted in (21). Hence,the maximum velocity of fluidumaxin the Courant condition was replaced asumax→V∕tanβ, and we defined a new numerical condition, namely, an MPS-slamming condition,as follows:

whereCslmis an MPS-slamming number. The MPS-slamming condition indicates that the optimum time step size is decided once the MPS-slamming number, slamming velocity, deadrise angle of the wedge, and particle size are decided. We investigated whether the MPS results are characterized by the MPS-slamming condition and how results change with the values of the MPS-slamming number. In addition, the optimum MPS-slamming number was determined for obtaining reasonable results without further deliberate tuning of numerical conditions.

3 Numerical Results

3.1 Physical and Numerical Settings

2D wedge slamming was simulated by the MPS. A general description of the computational situation is shown in Figure 1, whereWandDare the width and depth of the numerical rectangular water tank, respectively;B,d, andβare the width, thickness, and deadrise angle of the wedge,respectively; andVis the forced slamming velocity (constant value). For the boundary condition of the wall, we imposed the Neumann boundary condition, where the flux is zero at the wall (Koshizuka and Oka 1996). In this study, the wedge width was fixed asB=0.8m, and the thickness was set asd=4l0. The rectangular tank with widthW=2.4m and water levelD=1.2m was used. Note that the tank size was set to ignore wave reflections from the wall and guarantee convergence of numerical results. The physical parameters were set as follows: gravitational accelerationg=9.81m∕s2, fluid densityρ=1000kg∕m3, and kinematic viscosityν=1.0×10−6m2∕s.

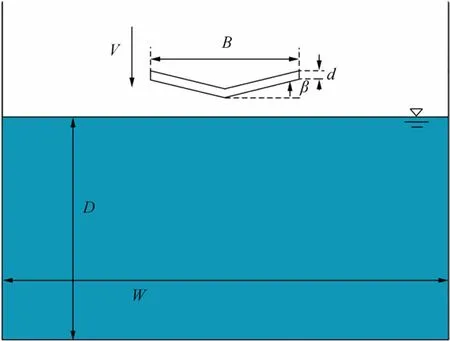
Figure 1 General description of wedge slamming

For the validation of the MPS simulations, the numerical results simulated by OpenFOAM (Chen et al. 2019) were used as the reference. Their results were verified by a grid refinement study and validated by using the simulation data of the BEM (Zhao and Faltinsen 1993). The sensitivity of MPS simulation results to physical and numerical parameters (i.e., slamming velocityV, deadrise angleβ, particle sizel0, time step size Δt, and MPS-slamming numberCslm) were investigated using the MPS-slamming condition in (26).

Although the present MPS is composed of tuningless schemes, it is necessary to decide a few numerical parameters: radius of influencere=2.4l0, Courant numberCCFL=0.2 (used in (10), and thresholds of the HGεHG=0.05 andNHG=3. These parameters are invariant for following all computations.

3.2 Numerical Results and Discussion

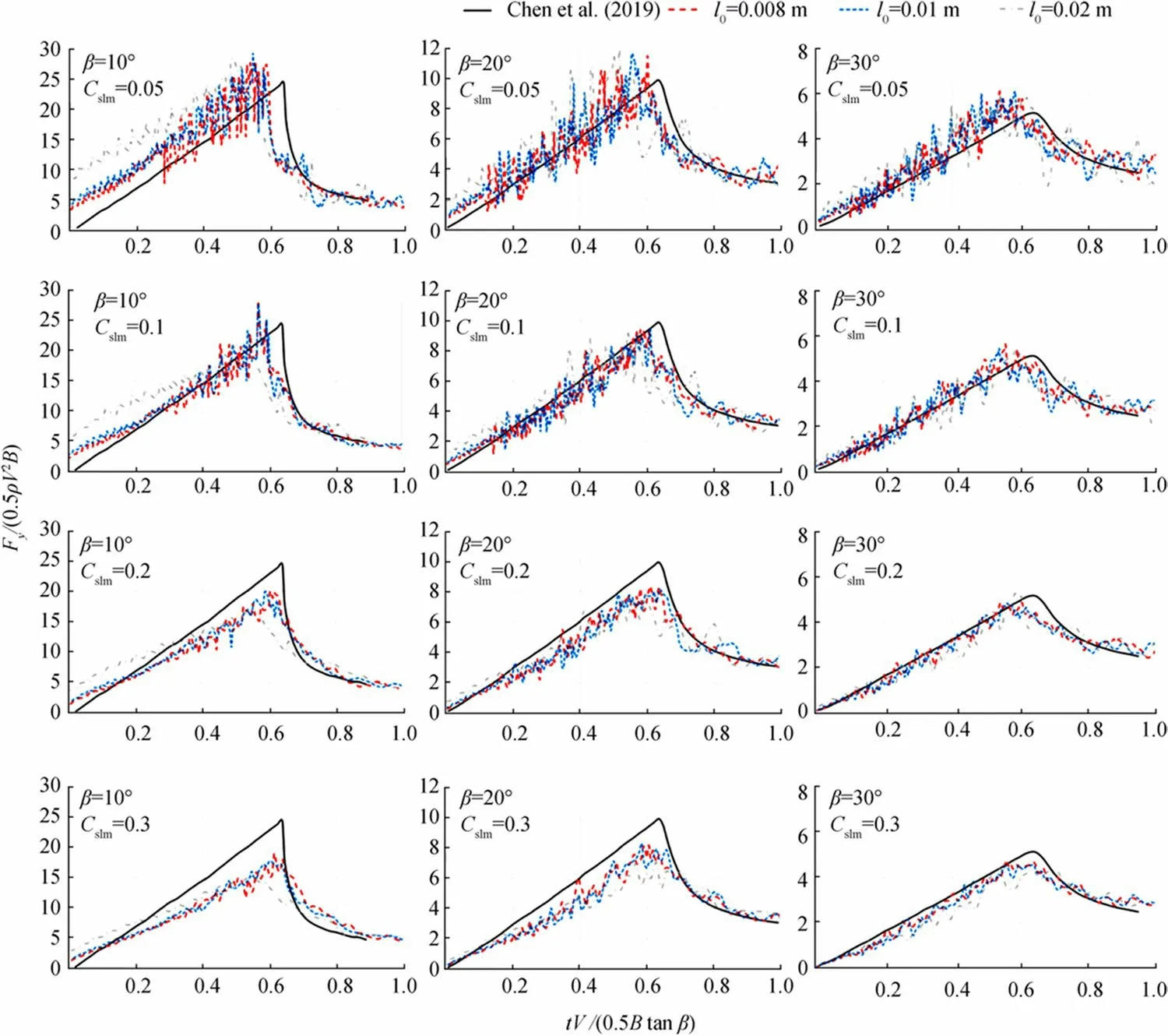
Figure 2 Vertical force versus deadrise angle β and MPS-slamming number Cslm. Results are compared with the numerical results by Chen et al. (2019).The slamming velocity is constant as V =2.0m∕s

We investigated the sensitivity of the simulation results to physical and numerical parameters using the MPS. First, the time histories of vertical forces acting on wedges are shown in Figure 2. The vertical forceFyand timetare normalized by the fluid densityρ, wedge widthB, slamming velocityV,and deadrise angleβ. The results were compared with those by Chen et al. (2019). Here, the slamming velocity was fixed asV=2.0m∕s. Twelve figures are plotted with respect to the deadrise angleβ(=10°,20°,30°) and MPS-slamming numberCslm(=0.05,0.1,0.2,0.3). The results of three different particle sizel0(=0.008,0.01,0.02m) are shown in each figure. Once the velocity, deadrise angle, particle size, and MPS-slamming number are decided, the time step size is calculated by the MPS-slamming condition (26). The use of a smaller deadrise angle, particle size, or MPS-slamming number indicates the use of a smaller time step size. In either case, the vertical force converges to Chen’s result after the peak. Therefore, the tank size is adequately selected. Focusing on one figure, the result ofl0=0.008m converges to that ofl0=0.01m despite the different time step sizes. Meanwhile, the result ofl0=0.02m shows a discrepancy. Generally, the results become similar flows if the slamming velocity, deadrise angle, and MPS-slamming number are the same and the particle size is small enough. Comparing different MPS-slamming numbers (e.g., cases ofβ=10°), we find a huge discrepancy in the slope and maximum value of vertical forces among four figures (e.g.,Cslm=0.05,0.1,0.2,0.3 inβ=10°). When the MPS-slamming numberCslm=0.3 is used, the maximum force is underestimated compared to that of Chen et al.’s result. As the MPS-slamming number is smaller (i.e., the time step size is smaller), the estimated vertical force is bigger. The result ofCslm=0.1 is close to Chen et al.’s result. However, the results are not converged to Chen et al.’s result when using small time steps. In fact, the result ofCslm=0.05 shows an overestimation of the vertical force. This fact indicates that the MPS suffers from bad convergence with the time step size. In addition, the disturbance of the force becomes bigger with the use of a smaller time step size. The above tendencies are found in different deadrise angles (i.e.,β=20°,30°). Moreover, the flow around the wedge is well characterized by deadrise angles as the MPS-slamming number is defined.

To quantitatively evaluate the convergence of the MPS results with respect to the time step size Δtand particle sizel0, a mean square error (MSE) between the MPS result and Chen et al.’s result was calculated, as shown in Figure 3.The MSE is defined among 0 ≤tV∕(0.5Btanβ)≤0.8, and the value is normalized by Chen et al.’s maximum vertical force. Three figures correspond to deadrise anglesβ=10°,20°,30°. In each figure, the normalized MSE versus the MPS-slamming numbers is plotted with three different particle sizesl0=0.008,0.01,0.02m. In all cases, the results ofl0=0.02m shows bigger MSE; the results ofl0=0.01m andl0=0.008m are in good agreement. Therefore, the MPS has convergence with respect to the particle size under the same MPS-slamming number, slamming velocity, and deadrise angle. As for the deadrise anglesβ=10°,20°,the results of the MPS-slamming numberCslm=0.1 show the smallest MSE although the results ofCslm=0.2 have a similar MSE value. As shown in Figure 2, the results ofCslm=0.1 show a seemingly better agreement with Chen et al.’s result than those ofCslm=0.2. However, the MSE results show almost the same errors, which may be because the results ofCslm=0.1 have a bigger disturbing oscillation than those ofCslm=0.2. Conversely, in the case ofβ=30°, the results show the smallest MSE whenCslm=0.3.Although the maximum force becomes bigger with smaller time step sizes, this influence is smaller than that of the disturbance of the force in this case. Nevertheless, the use ofCslm=0.1 to 0.3 inβ=30°is acceptable. Overall, the present MPS can give reasonable results using the MPSslamming numberCslm=0.1 to 0.2 except for the existence of a high disturbing oscillation. To suppress this noise, the biggerCslmshould be used (i.e., the smaller time step size Δtshould not be used).

Figures 2 and 3 are simulated by fixing the slamming velocity asV=2.0m∕s. Then, we investigated the sensitivity of the vertical force to the slamming velocity. The particle sizel0=0.01m and MPS-slamming numberCslm=0.1 were selected, and the results using different slamming velocitiesV=1.0,2.0,3.0m∕s were compared with Chen et al.’s results, as shown in Figure 4. In the figure ofβ=10°aroundt=0, vertical forces by the MPS do not start from zero.When the deadrise angle is small, the fluid particles on the surface are very close to the wedge. This geometrical arrangement induces the fuzzy free surface detection even though the wedge has not actually touched the water surface yet. This condition results in the non-zero value of the vertical force even att=0. For the results ofβ=30°andV=1.0m∕s, the converged force after the peak is different from the other results. Because the velocityV=1.0m∕s is small, the dimensional value of the force is also small.Therefore, the order of the dynamic slamming force is almost balanced with the order of the hydrostatic force, and the force is converged to the static force (i.e., buoyancy).Except for these cases, the MPS results show a good agreement with Chen et al.’s results. Hence, we can conclude that the proposed MPS-slamming condition can characterize the MPS results well, and similar flows are obtained using the sameCslm. Essentially, the use ofCslm=0.1 to 0.2 provides reasonable results for the present MPS simulations. The MPS-slamming condition here is 0.1 ≤VΔt∕(l0tanβ)≤0.2.This value might depend on the used schemes, so an adequate value ofCslmshould be investigated. Because the relation between physical and numerical parameters is characterized by the MPS-slamming number, a quasi-verification of the MPS could be performed using the proposed MPSslamming condition.

Figure 3 Mean square errors between the vertical force simulated by Chen et al. (2019) and that by the present MPS. Mean square errors are calculated among 0 ≤tV∕(0.5Btanβ)≤0.8 and normalized by the maximum vertical force

Figure 4 Vertical force versus deadrise angle β and slamming velocity V. Results are compared with the numerical result by Chen et al. (2019). MPSslamming number Cslm =0.1 and particle size l0 =0.01m are used

Finally, the pressure propagation process is shown in Figure 5 to visualize the flow around the slamming of the wedge. To validate the MPS results, the pressure field was also calculated using Wagner’s theory, i.e., (22) to (24). The left-hand side of the wedge at each figure is the pressure field calculated by Wagner’s theory, and that on the right-hand side is the simulation result by the MPS (pressure fields are the dimensional valuePPa). The left-hand figures are plotted using dummy particles whose positions and pressures are given by Wagner’s theory. For the MPS simulation,the MPS-slamming numberCslm=0.1, slamming velocityV=2.0m∕s, and particle sizel0=0.01m were used. Three time stepst=Δt,81Δt,161Δts are plotted. The actual time step sizes are different among different deadrise angles,which are calculated by the MPS-slamming condition. The overall pressure propagation processes are in good agreement. Looking at a snapshot ofβ=10°andt=Δt, the MPS result shows a dynamic pressure under the wedge, although the Wagner result does not have. This result is attributed to the crude detection of the free surface through parachute detection, as explained in the discussion of Figure 4. Generally, Wagner’s theory overestimates the pressure and vertical force, especially when the deadrise angle is small due to the use of the simplified boundary condition (Dobrovol’Skaya 1969) and linear Bernoulli’s equation (Korobkin 2004) and the lack of consideration of the air trapping phenomenon(Tajima and Yabe 1999). (Further reasons for the overestimation of Wagner’s theory are reviewed by Wang and Guedes Soares (2017).) Such a tendency is found in our comparisons; the pressure fields by the MPS are smaller than those by Wagner’s theory, especially in the case ofβ=10°.This difference is excessive around the pileup of the free surface. The current single-phase MPS might not be effective to solve the slamming with small deadrise angles (e.g.,β～0°) because the air trapping effect is important. For such cases, the multiphase flow should be considered. Khayyer and Gotoh (2016) showed that the multiphase MPS can reproduce the air–water interaction and simulate the slamming of a flat plate.

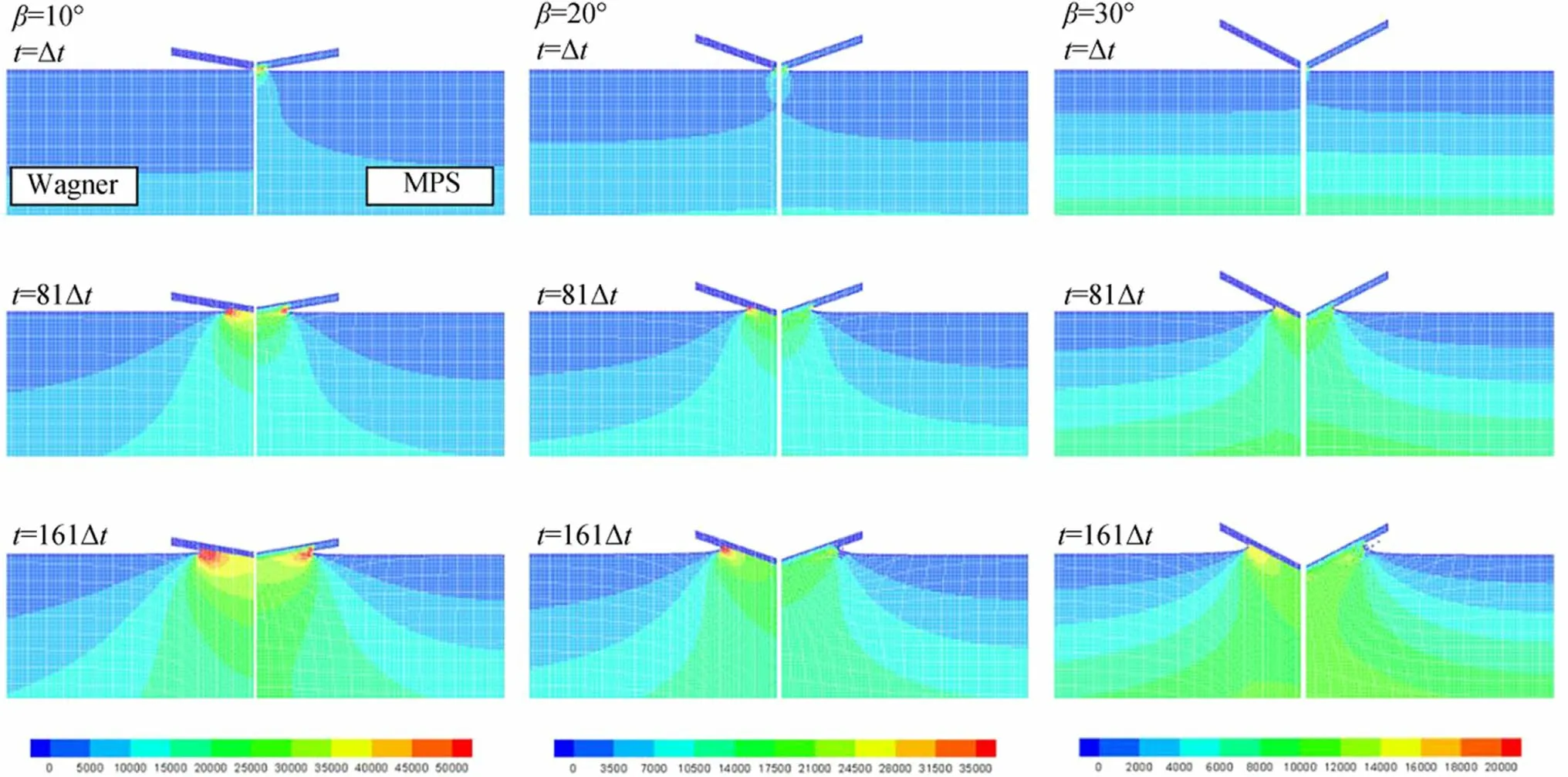
Figure 5 Snapshots of the pressure propagation process. Left side:pressure PPa solved by Wagner’s theory. Right side: pressure PPa simulated by MPS. For the MPS simulation, MPS-slamming number Cslm =0.1, slamming velocity V =2.0m∕s, and particle size l0 =0.01m are used. Three different times t=Δt,81Δt,161Δt s are shown

4 Conclusions

Because the MPS is poor at convergences with a time step size, this study investigates the sensitivity of the MPS simulation to numerical parameters. In particular, a 2D wedge slamming problem is considered. To eliminate the arbitrary tuning of the numerical parameters of the MPS, a practical numerical condition for the MPS simulation of the 2D wedge slamming (i.e., an MPS-slamming condition) is proposed. The MPS-slamming condition is made based on Wagner’s theory. The relation between the physical parameters (slamming velocity and deadrise angle) and numerical parameters (time step size and particle size) is connected by an MPS-slamming number. This finding indicates that the time step size is provided once the parameters are decided.The sensitivity of a vertical force to the parameters is also studied using different deadrise angles, slamming velocities,particle sizes, and MPS-slamming numbers. The simulation results are compared with those of OpenFOAM by Chen et al. (2019). This study shows that the estimated force is bigger and unphysical disturbance (noise) is harder as the time step size is smaller; the convergence with the time step size is not observed in the MPS simulation. Moreover,the MPS results become similar flows using the proposed MPS-slamming condition with the same MPS-slamming number. When the present MPS schemes are used, the use ofCslm=0.1 to 0.2 gives reasonable results for ranges of slamming velocities and deadrise angles. We believe that this MPS-slamming condition helps MPS users to verify and decide the numerical parameters without deliberate tuning.

FundingSupported by JSPS KAKENHI Grant No. JP19K15218.

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.