受电弓碳滑板异常磨损与高频振动机理分析

2021-03-25王安斌

铁道标准设计 2021年3期

黄超，王安斌，何宇，高锋

(1.上海工程技术大学城市轨道交通学院，上海 201620；2.上海工程技术大学航空运输学院，上海 201620)

引言

滑动电接触点作为弓网系统的纽带，是高速列车中的重要部分。电流从悬链线传递到受电弓为传动系统提供持续动力，然而受电弓与接触网的相对运动导致的离线现象会加剧电弧侵蚀磨损[1-5]，严重时甚至会造成列车供电中断，丧失牵引力和制动力。在弓网系统中碳滑板的摩擦磨损国内外学者进行了大量研究，CHO等[6]提出非线性滴管法和时间积分法的有限元公式，比较了接触线上的模拟动态应变与直接测量应变，并验证了振动试验中受电弓响应频率<50 Hz时仿真模型的正确性，说明该方法可用于准确分析架空接触线对移动受电弓的低频动态响应；AMBROSIO等[7]对比了0～20 Hz频率范围内通用受电弓集总质量模型与物理原型的频率响应函数，研究了最小化碳滑板与接触网的接触力标准偏差，表明优化过程在标准悬链上改进现有设备性能的空间相当有限；WEI等[8]建立了计算磨损率模型，可大致预测接触线和碳滑板的磨损，给出了一种估计和预测碳滑板磨损轮廓的方法，结果表明，预测与实际磨损具有良好的一致性；周宁等[9]基于有限元法分析了弓头和接触网的相互作用，结果表明，频率高于20 Hz时，40～100 Hz的频率分量在碳滑板接触力和加速度频谱中占较大比重。

然而，上述研究多数基于弓网系统的磨损模型和碳滑板低频振动响应得出的结论，当碳滑板在高速运行时弓网系统产生特定形态的振动，其中有害的高频振动也会间接引起或加剧碳滑板的异常磨损[10]。目前，受电弓碳滑板高频振动与异常磨损形态的研究较少，因此研究和抑制弓网系统中碳滑板的有害高频振动，确保受电弓与接触网之间的合理运动与匹配具有重要意义。

本文利用理论与实验相结合的模态分析，将受电弓碳滑板的模态参数与异常磨损形态对比分析，得出引起异常磨损的有害高频振动范围，并采用多参数法对碳滑板优化设计，为受电弓碳滑板的异常磨损研究提供可行性思路。

1 受电弓动力学模型及运动微分方程

受电弓是安装列车顶部从接触网上获取电流的设备，从结构上主要分为单臂受电弓和双臂受电弓两类，而双臂由于设计结构的限制和运行过程中气动噪声过大等问题，逐渐被单臂受电弓所代替，具体构件一般包括：底架、下臂杆、上臂杆、连杆、平衡杆、升弓弹簧、弓头支架、滑板、弓角等机械连接而成，为了简化计算，只考虑受电弓的垂向运动，如图1所示。

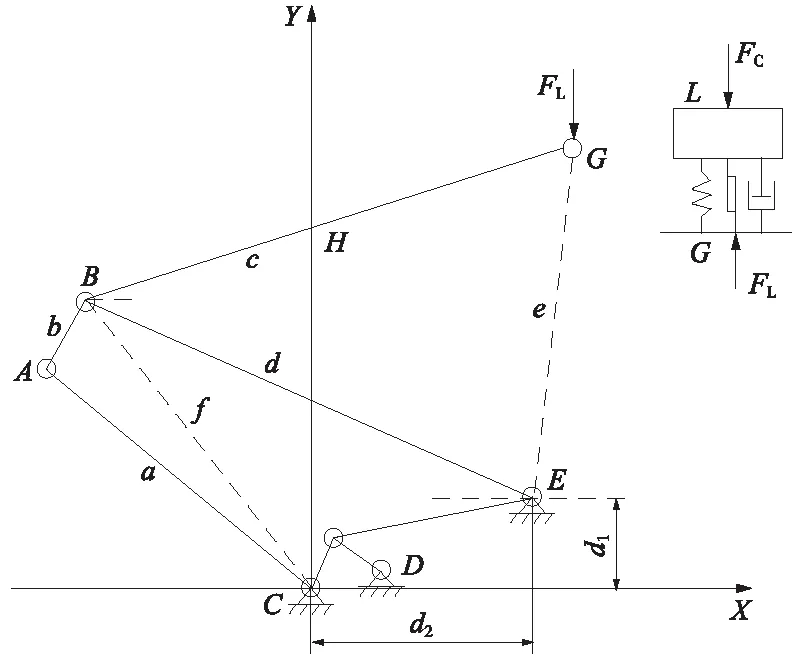
图1 受电弓简化垂向结构计算模型

由图1可见，A、B、C、E表示下臂杆和撑杆各绞点，虚线为模型中计算过程的辅助线，a、b、c、d代表各臂杆，d1和d2为E绞点的纵坐标和横坐标，L表示弓头位置，G表示上臂杆顶点，H为上臂杆形心，到绞点B的距离为d3，FC为弓头所受接触力，FL为弓头与受电弓系统相互作用力。根据简化模型，易于得出弓头的运动微分方程，取广义坐标下撑杆与X轴负方向夹角为θ，下臂杆与X轴负方向夹角为φ1，上臂杆与X轴正方向夹角为φ2，BC与撑杆的夹角为φ3，由三角函数

(1)

于是φ1、φ2、yG和(xH，yH)均可表示为θ的函数

(2)

(3)

yG=fsin(φ1+θ)+csinφ1

(4)

xH=fcos(φ1+θ)-d3cosφ1;

yH=fsin(φ1+θ)+d3sinφ1

(5)

将上述公式(2)～(5)对θ取变分，可得

(6)

令wa、wc、wd分别为撑杆、上臂杆和下臂杆的角速度变分，vyG为G点垂向速度，vxH、vyH分别为G点的横向速度和垂向速度，可表示为

wa=dθ/dt;wc=k2wa;wd=k1wa;

vyG=k3wa;vxH=k4wa;vyH=k5wa

(7)

由第二拉格朗日方程可得，广义力中有一部分为势力，表示为

(8)

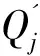
(9)

V′=magasinθ+mdgdsinφ1+mcgcsinφ2

(10)

式中，J为绕质心的转动模量；m为臂杆的质量；主动力作的元功表示为

(11)

式中，C为阻尼装置的阻尼数；C(ds/dt)为阻尼力。

基于上述理论，弓头的运动微分方程表示为

KL(yL-yG-yk)+MLg

(12)

2 受电弓碳滑板模态分析

2.1 理论模态分析

选取某地铁现有单条复合材料碳滑板进行模态分析。采用Solid-Works三维软件建立碳滑板的3D模型，导入ABAQUS有限元软件进行数值计算。参数设置如表1所示。

表1 受电弓滑板材料参数

根据公式(12)，采用ABAQUS有限元软件计算受电弓滑板的前6阶模态振型和模态频率，X、Y、Z三个方向表示受电弓滑板的纵向、横向和垂向，为了验证受电弓滑板理论模型的正确性，主要给出垂向振动模态振型和频率计算结果，如图2所示。

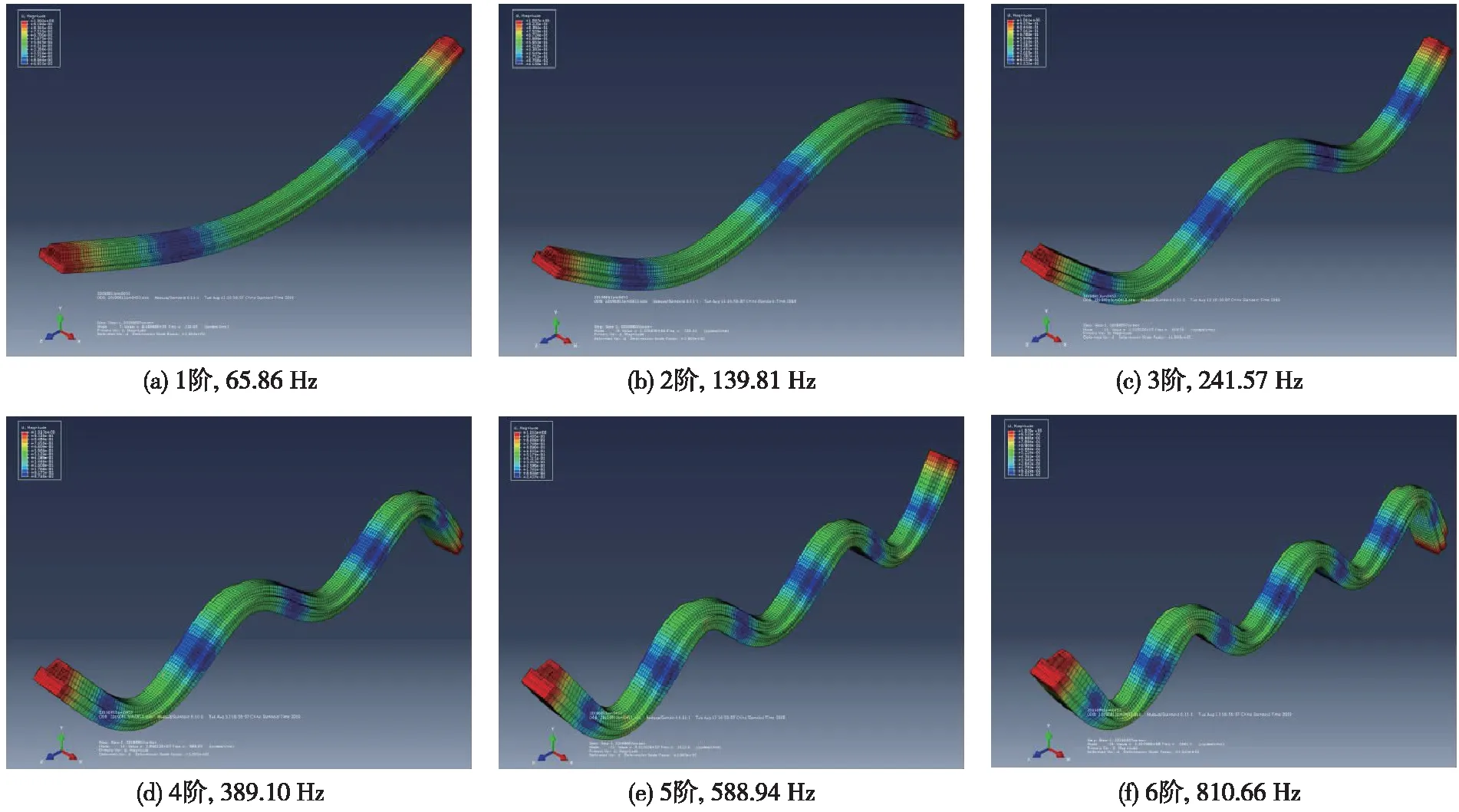
图2 碳滑板前6阶仿真垂向模态振型与模态频率

2.2 模态试验分析

考虑碳滑板在服役状态下的振动特性，垂直方向和横向的振动与受电弓碳滑板异常磨耗最为相关。垂向振动影响弓网系统的动态接触压力，接触压力异常会引起碳滑板的过渡磨损，同时碳滑板磨损的增加又会影响接触压力的变化；横向振动影响弓网系统的相对动态滑动过程，随着滑动速度的增加，导致电弧异常放电不断增加，碳滑板裂纹和深度有不断增加的趋势。本文分别对碳滑板的垂向和横向振动特性进行模态试验分析。

采用频域分析法进行碳滑板的模态参数识别，试验通过多点激励多点响应[11](MIMO)的方式。碳滑板振动加速度为测试指标，选用INV9310型力锤激励工具，接收端为352C33型号PCB加速度传感器，数据采集系统选用INV3060V系列高性能数据采集仪，数据处理系统采用配套的DASP工程版动态分析测试平台。在每一组测试中均进行多次激励和采样，对测试数据平均处理来消除频响函数的误差及试验过程中的背底噪声干扰。测试流程如图3所示。

图3 碳滑板模态试验流程

图4为垂向和横向模态试验的相干函数曲线，从图4可见，0～1 000 Hz频率范围内垂向模态频率和横向模态频率处相干系数接近1.0，说明模态试验的测试数据有效，外界干扰小，能真实反映出碳滑板的振动特性。图5表示了垂向和横向模态试验的频率响应函数曲线，反映了脉冲激励工作时对振动频率的衰减和放大作用，频率响应函数曲线中波峰对应的频率为模态频率[12]。对比图5(a)和图5(b)可见，垂向模态的加速度导纳峰值在第3阶到第5阶变化较为平缓，而对应的横向模态加速度导纳峰值波动较大，同时，横向模态所对应的每一阶模态频率均大于垂向模态。表2为前6阶垂向模态试验与仿真计算结果对比，得出模态频率最大相差5.03 Hz，误差均不超过3.4%，说明模态试验与仿真计算有较好的一致性，验证了有限元模型的正确性。对比图6(a)和图2，可以看出模态试验与仿真计算的前6阶垂向模态振型弯曲分布相吻合，试验模态振型振动变形处幅度较小和边界处弯曲较小，这是由于实际实验时界面滑移效果会影响碳滑板的刚度，且边界处由2个橡胶绳固定，振动发生抵消影响了边界处振动变形。

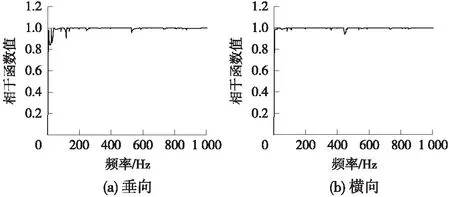
图4 碳滑板模态试验相干函数曲线

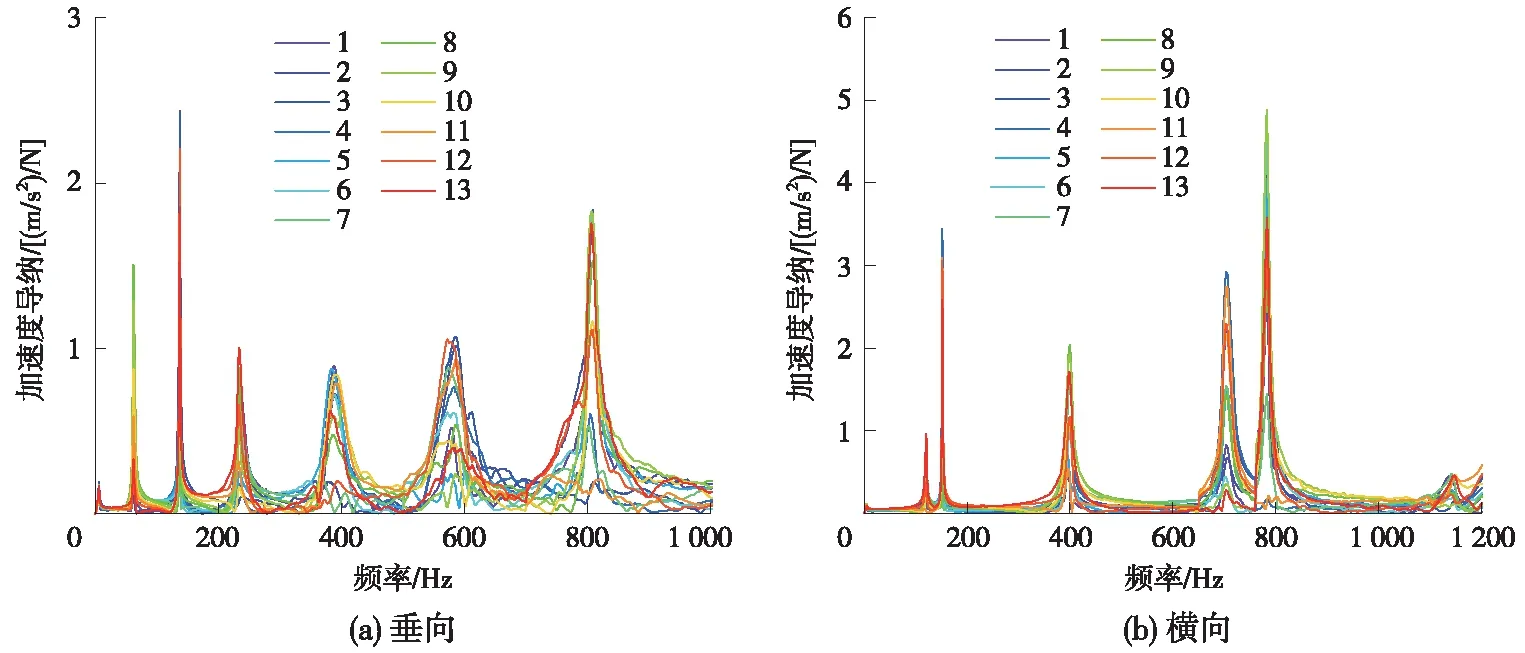
图5 碳滑板模态试验频响函数曲线

图6 受电弓碳滑板模态振型示意

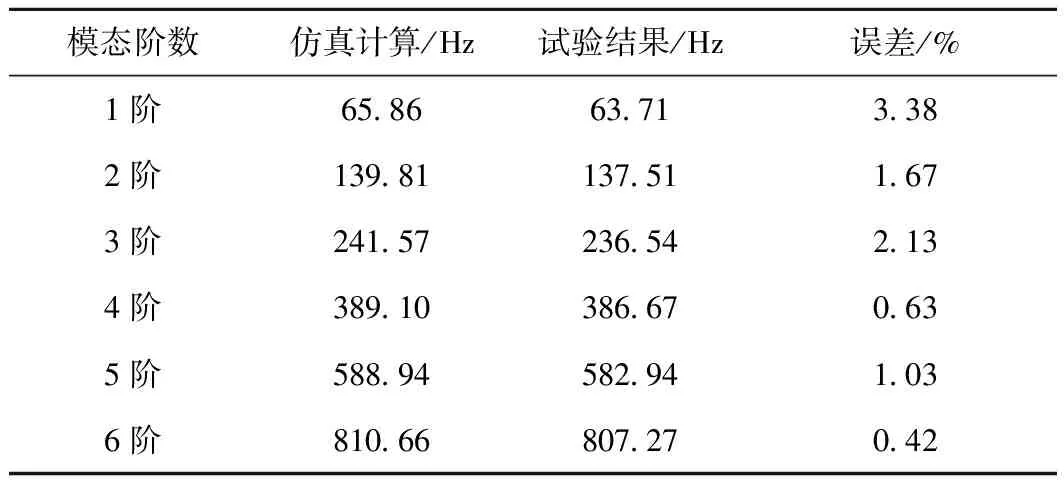
表2 碳滑板理论计算与试验结果垂向模态频率

2.3 异常磨损与高频振动分析

2.3.1 垂向振动

由于服役状态下碳滑板与接触网的相互作用及接触产生一个非稳态的动态作用力F，如图7(a)所示。在高速运行下，接触网的动态抬升量会显著变化，两者之间会产生接触力Fc，可表示为Fc=K(yL-y1)；yL、y1分别表示在同一时刻接触线和碳滑板的位移。当碳滑板发生高频振动或者遇到弓网间的“硬点”时，接触压力会迅速下降，在接触压力为0时，就会出现离线现象[13]，而受到外力作用的碳滑板产生的振动冲击与接触网相互碰撞，从而形成“接触—离线—碰撞—接触”的非稳态过程。同时，由于接触网及受电弓位置的变化使抬升量形成非稳态的波动而导致接触压力的波动，当碳滑板与接触网在这种波动的接触压力及外界例如运行过程的空气动态力等的激励，各种对碳滑板的动态激励导致碳滑板的振动，特别是高幅度的模态振动，反过来影响接触压力的变化。当接触压力增加，碳滑板与接触网的摩擦力随之增加，从而机械磨损增加；同时这种非稳态的接触压力，特别在“接触—离线—碰撞—接触”状态时，电弧磨损也会增加，因而接触网的动态抬升量会同时产生机械摩擦磨损和电弧磨损。研究表明，碳滑板垂向振动加速度与电弧放电能量有明显的相关性[14]，碳滑板振动加速度对碳滑板磨损率与摩擦系数的影响[15]变化曲线如图8所示。

图7 碳滑板与接触网相互作用示意

图8 磨损率与摩擦系数变化曲线

观察整个曲线可以看出：碳滑板摩擦系数随着垂向振动加速度的增大有较明显的下降趋势，且在振动较大时，加速度超过12.5 m/s2，电弧放电情况比较剧烈，由此产生的高温会造成接触线表面发生熔融，使得接触幅面摩擦力减小从而降低了摩擦系数；而磨损率随着垂向振动加速度增大而呈现增大的趋势，与摩擦系数变化类似，当加速度超过12.5 m/s2时，磨损率会急剧增大，这是由于当垂向振动较大时，离线现象明显产生的高温加剧了材料的氧化和黏着磨损。

2.3.2 横向振动

当受电弓碳滑板高速运行时，除了垂向振动改变摩擦力及接触状态引起的摩擦磨损外，由于两者运行中的滑动和摆动，碳滑板和接触网的横向及纵向滑动不可避免，在列车运行过程中碳滑板和接触网的准静态滑动的同时又附加了高频相对振动，这种附加的高频振动会大大地加速相对滑动量及磨损量。在固定车速时，碳滑板被激起的横向振动以及垂向分量导致接触压力波动和横向交变滑动[16]，横向-垂向相互作用模型如图7(b)所示，不仅会加剧垂向振动引起的磨损，而且在横向会扩大磨损范围。同时，随着车速的增加，会引起弓网间相对滑动速度的增加，不仅增加了机械磨损时产生的摩擦热，且由于横向振动的影响，碳滑板棱角处会首先与接触网碰撞，进而碳滑板侧边会出现冲击掉边的情况。

2.3.3 异常磨损轮廓

图9为碳滑板异常磨损二凹槽和三凹槽轮廓与模态振型的拟合示意，红色虚线表示模态振型的弯曲形状，根据图6(a)，可以看出碳滑板二凹槽与第3阶模态振型形状相吻合，碳滑板三凹槽与第5阶模态振型形状相吻合，说明服役状态下碳滑板激起的第3阶垂向模态频率约240 Hz和第5阶垂向模态频率约580 Hz分别为二凹槽和三凹槽异常磨损的主要有害高频振动频率。

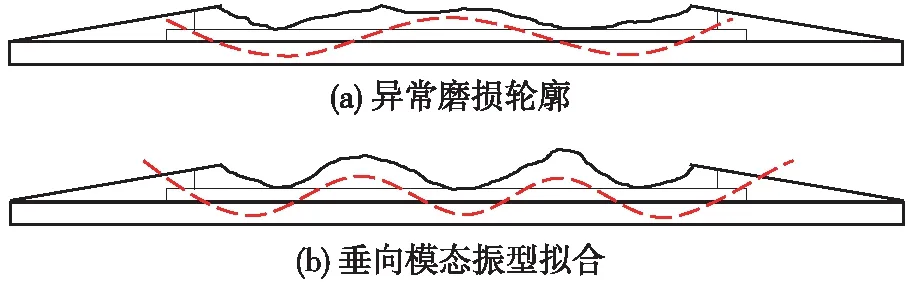
图9 异常磨损轮廓与垂向模态振型拟合示意

3 优化设计分析

3.1 优化设计理论

根据碳滑板异常磨损分析结果，改善碳滑板的高阶有害振动是降低异常磨损现象的有效方法，因此各阶模态频率大小和垂向振动加速度是评价碳滑板振动特性优化效果的两项重要指标。本文考虑碳滑板的结构和阻尼参数两个方面设计优化方案[17-19]，可以得出，优化设计方案是一个多目标、多参数优化问题，数学模型可以表示为

(13)

式中，q1，q2为目标函数，分别表示优化后的垂向振动加速度峰值和各阶模态频率；ηc和sc为设计变量表示阻尼参数和碳滑板截面面积；ωc表示优化前各阶模态频率；Δm/m0和abs(Δωi)/ωi表示碳滑板结构质量相对增加和各阶模态频率相对变化的上限值。其中，目标函数可设计为

(14)

(15)

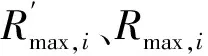
根据优化模型和现有实验环境进行实例分析，分为不同截面碳滑板[20-21]和不同阻尼参数两种设计变量进行模态实验对比分析，由图9中磨损轮廓得出，在磨损最深部位为响应峰值，因此采用单点输入单点输出模态试验方法可看出最佳效果。信号激励点与响应点如图10所示，红色箭头表示激励点，黑色箭头表示响应点。

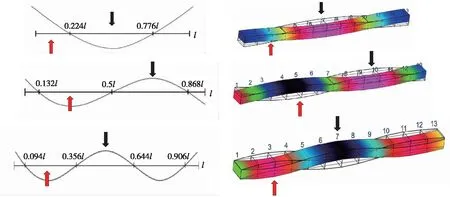
图10 激励点与响应点位置分布

3.2 碳滑板不同阻尼参数的对比分析

采用与2.2节中的实验原理和环境，选取与2.3节中磨损与振动机理相同的某地铁现有碳滑板，通过不同的阻尼参数[22]设计3种方案进行力锤激励敲击试验并进行模态参数对比分析。3种设计方案里，方案1是原来的碳滑板结构；方案2是改变原来碳滑板铝基的质量和增加阻尼，其质量是方案1的1.2倍；方案3是进一步改变原来碳滑板铝基的质量和增加阻尼，其质量是方案1的1.4倍；这3种结构里，各模态的阻尼特性有后续的模态试验给出。为了试验结果具有可比性，碳滑板截面均为梯形，且在这3种阻尼方案分别选取相同的激励点与响应点。多次实验选取输入力相同幅值的有效试验结果，3种方案的模态参数如表3所示。

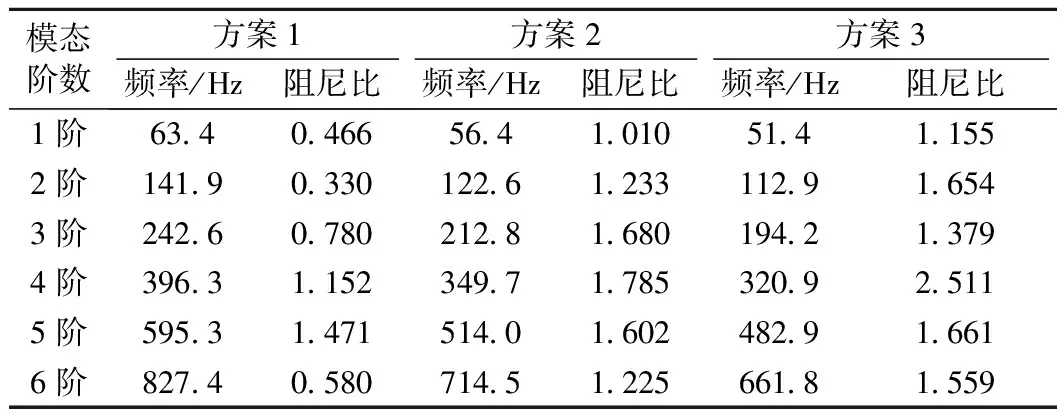
表3 梯形碳滑板在不同阻尼参数的模态频率与阻尼比

如图11(a)所示，比较不同阻尼参数的振动响应特性的传递函数响应峰值，在第3阶模态、第5阶模态和第6阶模态处效果尤其明显，在第3阶模态处，如图中虚线区域所示，方案2比方案1传递响应函数响应峰值降低5 dB，约4.1%，方案3比方案1降低了6 dB，约4.8%；在第5阶和第6阶模态处具有相同的变化趋势。结合表3，比较3种方案的模态频率与阻尼比，方案2各阶模态频率均大于方案3阻尼，但都小于方案1，而阻尼比与模态频率的变化趋势相反；其次，优化后的第1阶模态改变的频率范围和加速度幅值较小，由于阻尼隔振机理，底阶模态频率决定了振动传递特性与隔振范围，表3中方案3的第1阶模态频率最低，阻尼比最大，说明此方案的隔振范围更宽，隔振效果更加明显。由于激励点不同，对比图11(a)、图11(b)、图11(c)中激起的第3阶模态响应幅度较小，然而优化后的效果仍较明显。

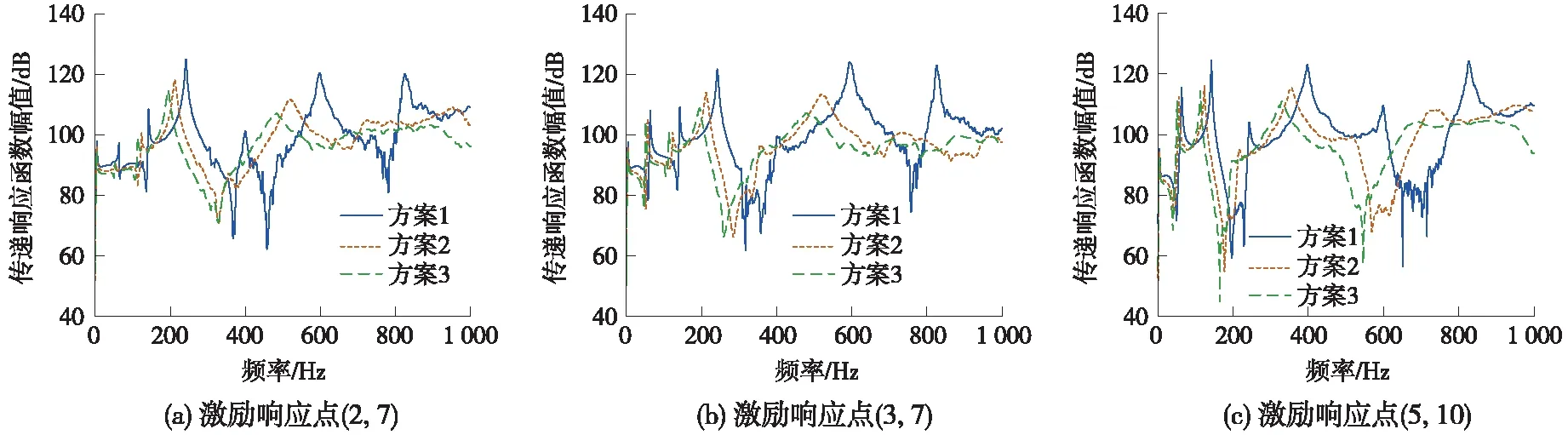
图11 梯形截面不同阻尼参数传递函数响应对比

3.3 碳滑板不同截面对比分析

图12为梯形(TC)和矩形(RC)截面的碳滑板示意，与3.2节相同的实验方案对矩形截面的碳滑板进行模态试验分析。

图12 梯形和矩形截面碳滑板

对比图13(a)和图11(a)，可以看出矩形截面在方案2、方案3与方案1对比传递函数响应峰值比梯形截面下降的幅度更大，在第3阶模态和第5阶模态处尤为明显，第3阶模态方案2峰值下降19 dB，约15.7%，方案3峰值下降22 dB，约18.1%，第5阶模态方案2峰值下降27 dB，约21.1%，方案3峰值下降33 dB，约25.8%；如表4所示，表示在激励响应点(2，7)方案2、方案3对比方案1的传递函数响应峰值下降幅度及误差，方案2、方案3下的振动传递响应函数响应峰值下降效果矩形截面更明显，而第4阶模态处出现了负值，则说明方案3下并没有激起第4阶模态。而图13(b)看出方案3与方案2效果相差明显，则表示方案3对于碳滑板隔振优化效果没有方案2稳定。

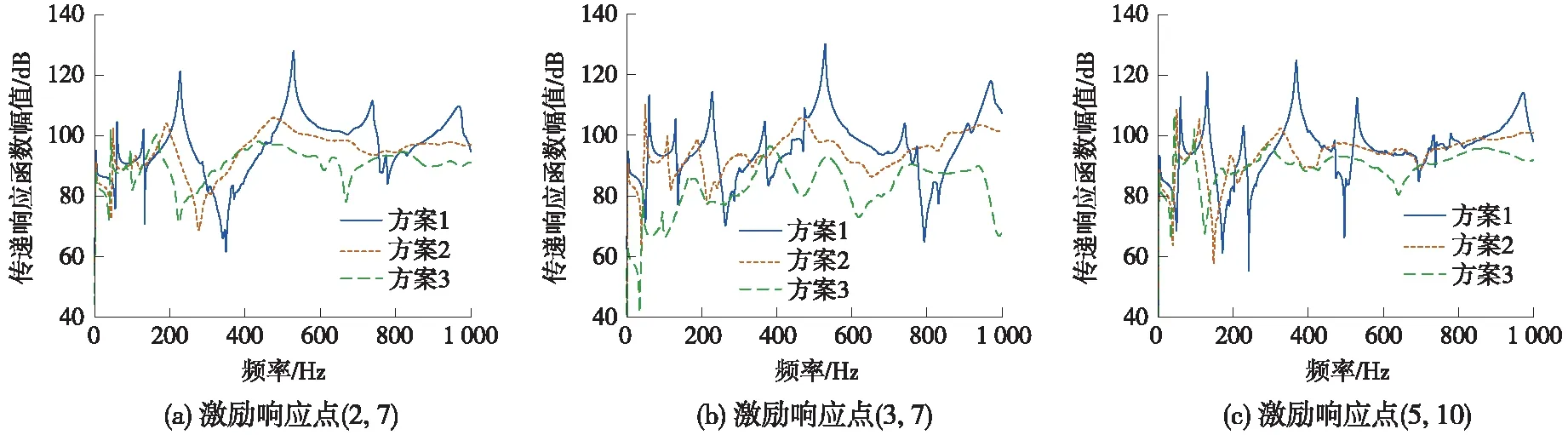
图13 矩形截面不同阻尼参数传递函数响应对比

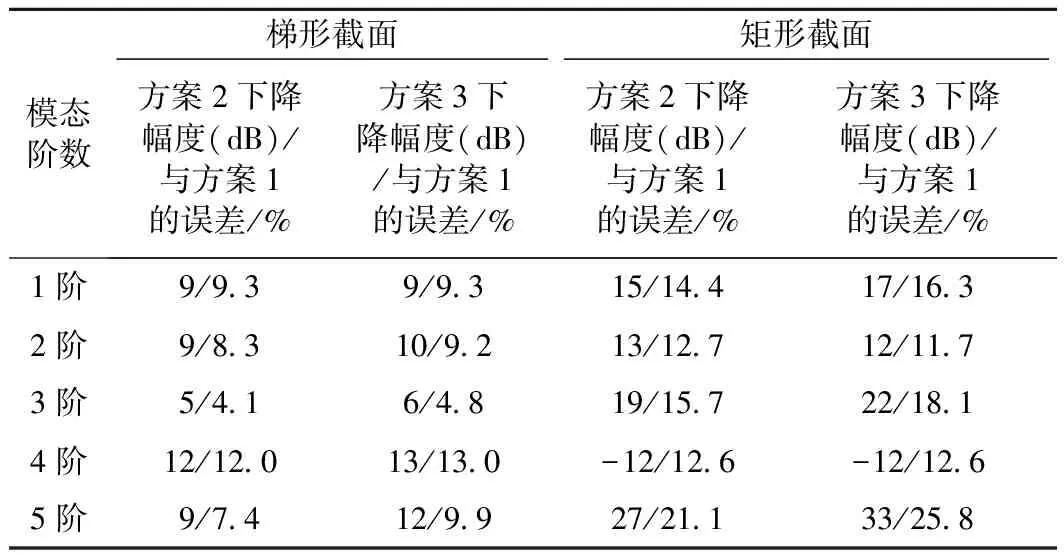
表4 方案2、方案3对比方案1的传递函数响应峰值下降幅度及误差

综上所述，对于碳滑板高频有害振动为异常磨损中重要因素之一，根据3.2节和3.3节的试验结果，表明不同的阻尼参数和不同截面对传递函数响应峰值改变不同，方案3比方案2对降低模态频率、降低振动加速度响应峰值(dB)效果更明显，若考虑材料质量、价格和碳滑板振动的稳定性，方案2效果更好；矩形截面比梯形截面对振动加速度响应峰值(dB)的下降更明显，能更有效地避开有害的高频振动且降低了振动加速度响应峰值，从而降低碳滑板异常磨损量。表5可见方案3比方案2的q1指标值更小，q2指标值更大，矩形截面比梯形截面的q1指标值更小，q2指标值更大，与上述得出结论一致，说明了优化模型的正确性。