高速铁路典型牵引变电所回流异常分析与抑制方案研究

黄文勋

(轨道交通工程信息化国家重点实验室(中铁一院)，西安 710043)

引言

我国高速铁路采用单相工频交流制牵引供电系统和单边供电模式，牵引回流以钢轨、大地和其他线缆作为通路返回牵引变电所[1-2]。目前已开通运营的线路有部分牵引变电所存在地网回流比例偏大、同一变电所两供电臂回流占比差不同、环境条件类似的相邻牵引所回流占比明显差异等问题。过大的地回流存在加剧牵引变电所主地网腐蚀、抬升牵引变电所地电位以及烧损线缆接头等风险[3-6]。工程实际中牵引变电所各牵引回流路径占比受到多项因素影响，文献[7-8]基于近年高速铁路联调联试实测数据，研究了牵引回流分配指标的变化规律；文献[9-10]研究了城市轨道交通中回流系统及钢轨电位特性；文献[11-12]分析了在隧道及站场中牵引回流系统特性；文献[13-14]分析了综合接地对钢轨电流及电位的影响；文献[15-17]分析了牵引变电所地回流与变电所及分区所地网电阻、土壤电阻率、电力机车位置等之间的关系；文献[18-19]研究了牵引变压器接线形式、牵引网供电方式、电力机车类型、钢轨泄漏阻抗等因素对钢轨电位的影响。上述文献在牵引变电所地网回流占比分析中，对接触网与钢轨间电磁耦合、钢轨大地间传导、牵引变电所接地电阻等因素的影响进行了分析，但均未考虑牵引变电所变压器中性点端子与钢轨间连接的回流导线(以下简称N线)影响。

本文基于高速铁路牵引供电系统回流分布模型，给出了包含N线影响的不同位置钢轨电位和电流计算公式，分析了N线阻抗变化对牵引回流的影响。结合实际工程案例，得到了不同设计参数下牵引回流分布规律，得出了牵引变电所地网回流过大的原因，并有针对性地提出了抑制方案。对比工程整改前后的差异，验证了上述模型分析和解决方案的正确性，对高速铁路牵引回流系统优化设计提供了重要参考。

1 考虑N线影响的直接供电方式下钢轨电流、电位理论计算分析

高速铁路牵引供电系统采用综合接地，牵引电流沿着钢轨、贯通地线、PW线(回流线)、大地及N线返回牵引变压器。根据研究目的，将钢轨、贯通地线、PW线(回流线)可以用等效钢轨代替。以单线为例，牵引网等效电路如图1所示。

图1 单线牵引网等效电路

如图1所示，接触网—地和钢轨—地回路的自阻抗分别z1、z2，这两个导线—地回路之间的互阻抗z12，钢轨—地之间的单位长分布导纳y。假设钢轨的参数均匀分布且无限长，两根钢轨并联，电流分布相同。

考虑N线阻抗及N线与供电线互阻抗的钢轨各区段电流、电位计算方法推导如下。

1.1 0≤x≤l区段

如图1所示，在0≤x≤l区段，由传输线理论，钢轨电位、电流在x正方向上有

(1)

式(1)整理得

(2)

式(2)的通解为

(3)

以下根据边界条件求A、B。

条件1：在牵引变电所处，根据图1可得出如下等式

(4)

式(4)中，ZN为N线阻抗；ZE为牵引变电所接地电阻；KN=ZFN/ZN为N线与供电线感应系数。

对式(4)进行整理，有

(5)

条件2：在机车处(x=l)，可得

整理可得

(6)

将式(5)代入式(6)可求得

(7)

因此，将式(6)、式(7)代入式(3)，可求得0≤x≤l区段钢轨电流、电位为

(8)

1.2 x<0区段

如图1所示，在x<0区段，由传输线理论，钢轨电位、电流有

(9)

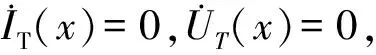
当x→0，由于电位的连续性，可得

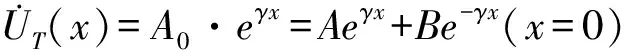
(10)

将B0=0及式(10)代入式(9)，即得x<0区段的钢轨电流、钢轨电位计算公式。

1.3 x>l区段

如图1所示，在x>l区段，由传输线理论，钢轨电位、电流有

(11)

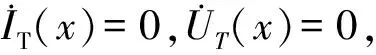
当x→l，由于电位的连续性，可得

即

(12)

将Al=0及式(12)代入式(11)，即得x>l区段的钢轨电流、钢轨电位计算公式。

2 考虑N线影响的AT供电方式下钢轨电流、电位计算

AT供电方式下的钢轨电流、电位计算，可以根据替代原理与叠加原理，利用牵引网电流与钢轨电位计算的“可解耦”性，在直接供电方式的基础上进行推导。第1个AT段的电路示意如图2所示。

由替代原理，图2(a)可用图2(b)所示的等值电路表示。根据叠加原理，图2(b)可分解为图2(c)与图2(d)。由于图2(c)中负馈线电流为零，相当于直接供电方式，即可用直接供电方式的式(8)、式(10)、式(12)计算钢轨电流、电位。

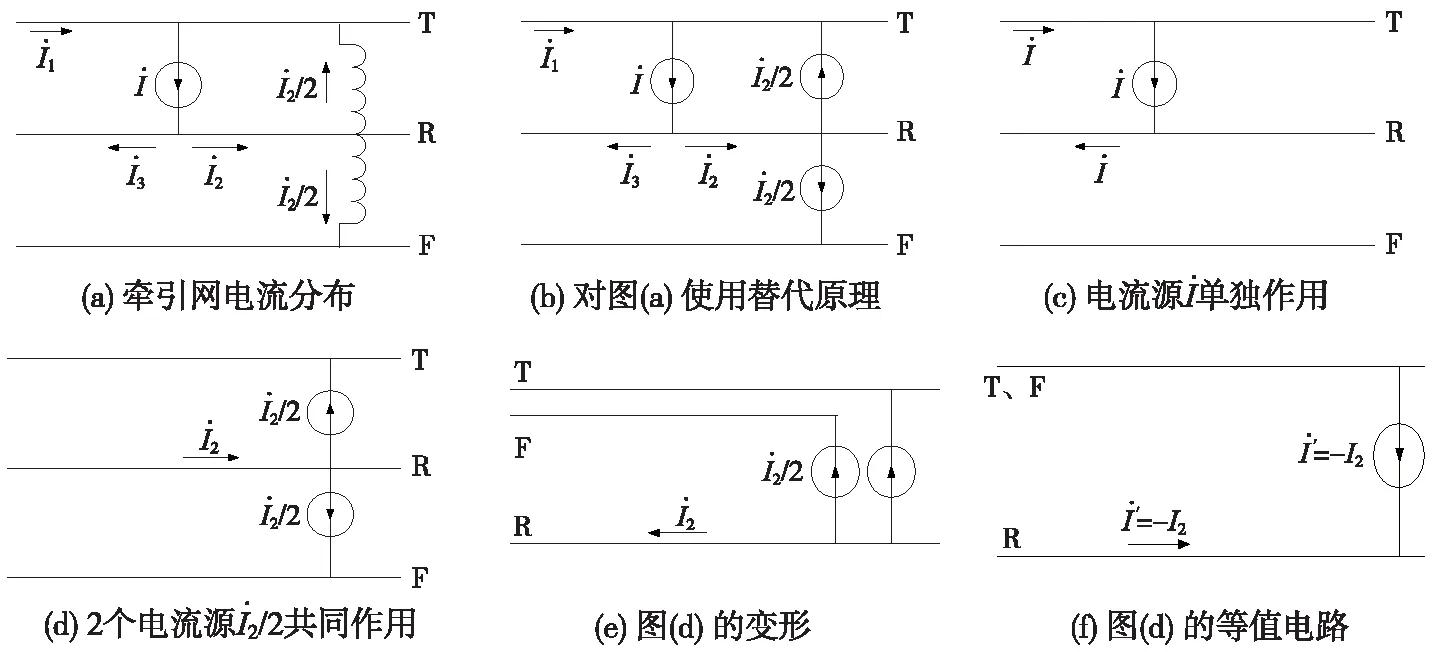
图2 第1个AT段钢轨电流、电位计算原理

图2(d)中，T与F线电流方向相同(均流向牵引变电所)，因此可以将图2(d)变形为图2(e)，因此可用图2(f)等值表示。将钢轨感应系数K=(zTR+zFR)/(2zR)代入式(8)、式(10)、式(12)，即可计算钢轨电流、电位。

复线、列车在第二个AT段、多列车运行等工况，可利用多导线理论[20]，在求得AT供电系统中列车、AT所、分区所等处电流后，使用叠加原理进行计算。

3 典型高速铁路计算

3.1 计算条件

以某典型的高速铁路为例，计算条件如下：

供电臂长25 km，AT所位于供电臂中部；

列车距牵引所10 km，列车电流为900 A；

钢轨对地泄漏电导为0.01 S/km；

牵引网采用CTMH150+JTMH120导线组合，PW线为JL/LB1A-125。

3.2 N线阻抗影响

设牵引变电所接地电阻为0.3 Ω，N线与供电线互感系数为0.3。当N线阻抗分别为0.1，0.4，0.7，1.0 Ω时，钢轨电流计算结果见图3。

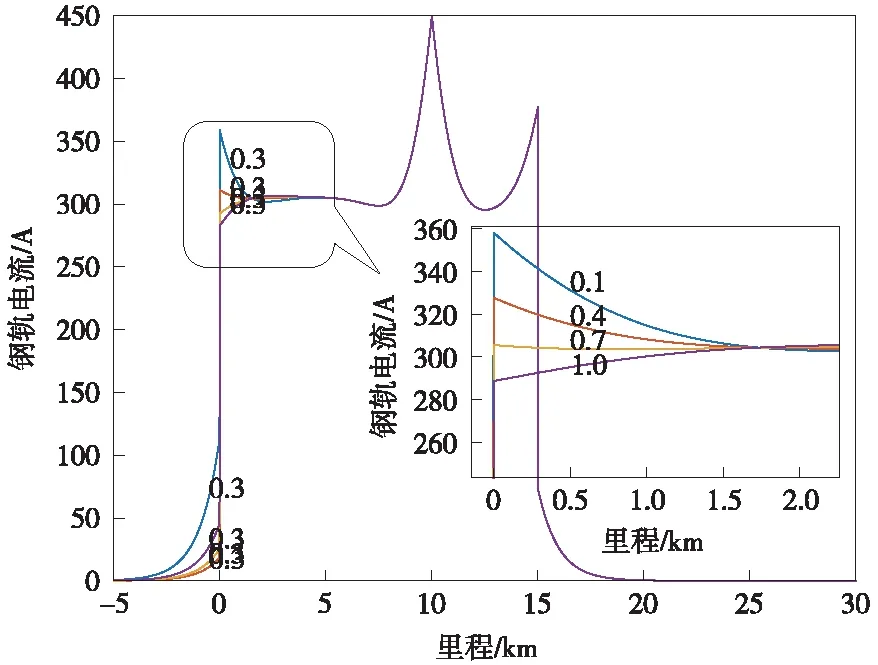
图3 不同N线阻抗钢轨电流计算结果

根据计算可见，随着N线阻抗增大，牵引变电所附近钢轨电流减小，即牵引变电所地网回流占比增大。

3.3 N线与供电互感系数影响

设牵引变电所接地电阻为0.3 Ω，设N线阻抗为0.4 Ω。当N线与供电线互感系数分别取0.1，0.2，0.3，0.4，0.5时，钢轨电流计算结果见图4。

图4 不同互感系数影响钢轨电流计算结果

由此可见，随着N线与供电线间互感系数的增加，牵引变电所附近钢轨电流增大，即牵引变电所地网回流占比减小。

3.4 牵引变电所接地电阻影响

设N线阻抗为0.4 Ω，当牵引变电所地网不同接地电阻时，钢轨电流计算结果见图5。

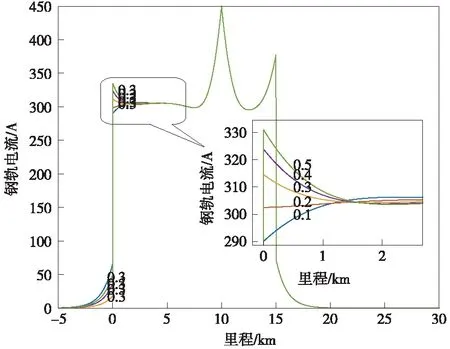
图5 不同牵引所接地电阻钢轨电流计算结果

由图5可见，随着牵引所接地电阻增长，牵引变电所近端钢轨电流将逐步增大，即牵引变电所地网回流占比逐步减小。

4 抑制方案

4.1 现场实测情况

对地网异常的某高速铁路牵引变电所进行测试。该项目速度目标值为250 km/h，牵引变电所进线电压等级为330 kV，牵引供电系统采用AT供电方式，牵引变电所两侧铁路均为桥梁形式。

分别在铁路线路上、牵引变电所回流接地箱处进行了测试。现场测试情况如图6所示，牵引变电所回流测试数据如表1所示。

图6 现场测试

4.2 数据分析及工程整改措施

根据表1可见，列车位于牵引变电所右侧时，牵引变电所地回流占比正常(<50%)，但当列车位于牵引变电所左侧时，牵引变电所地回流占比超标(>50%)。根据现场检查，两侧供电臂接触网与钢轨间电磁耦合特性、钢轨大地间传导特性均无明显差异。

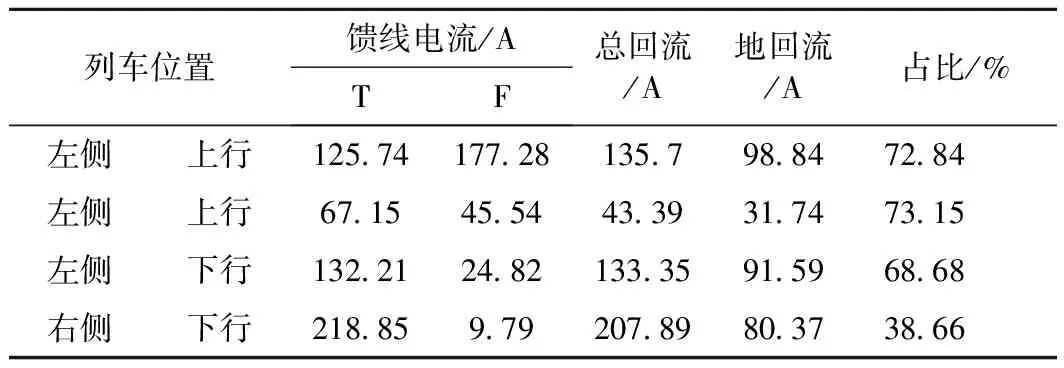
表1 整改前牵引变电所回流测试数据

为此，根据上节研究结论，结合现场情况，采取的工程措施如下。

(1)优化N线路径，通过在牵引所内重新挖沟敷设N线，避免N线迂回，降低N线阻抗。

(2)自牵引变电所向两侧最近扼流变压器增设绝缘悬挂的回流线(上、下行均采用单根JL/LB1A-250 mm2)。为增加N线与供电线互感系数采取措施：回流线尽可能采用架空架设；在供电线独立架设区段，与供电线合架；在无供电线区段，与接触网合架。

整改后，牵引变电所回流测试数据如表2所示。

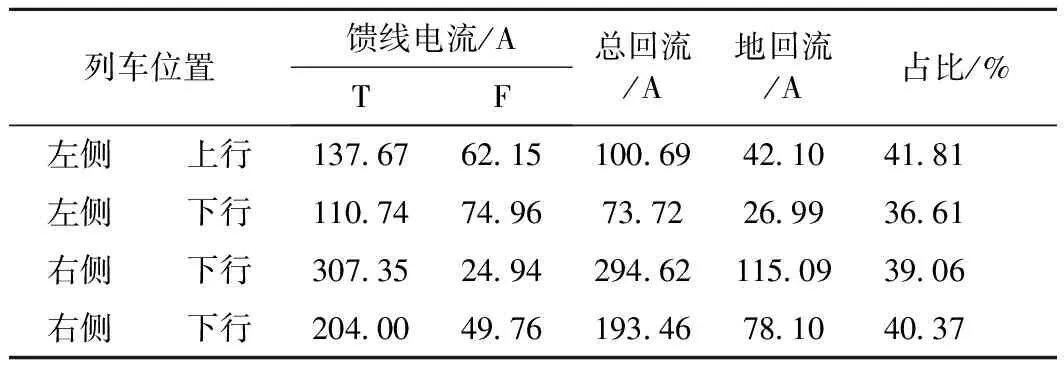
表2 整改后牵引变电所回流测试数据

根据表2数据，整改后，当列车位于该牵引变电所左侧时，地网回流占比降低，满足要求。

5 结论

本文对高速铁路牵引变电所回流异常情况进行了分析，主要结论如下。

(1)首先推导了包含N线阻抗及N线与供电线互感影响、带回流线直接供电方式下的钢轨电流、电位理论计算公式。然后，根据AT与带回流线直接供电方式的差异，利用替代原理与叠加原理，得出AT供电方式下钢轨电流、电位的计算公式。根据所得出公式，可以量化计算N线阻抗、N线与供电线间互感系数对牵引变电所回流的影响程度。

(2)提出了通过降低N线阻抗、增加N线与供电线互感系数以抑制回流异常的工程方案。经过实际工程实践，验证了抑制方案的工程效果。

(3)实际工程中，牵引变电所回流需在联调联试期间才进行测量。由于联调联试时大部分工程已经完成，一旦发现回流异常，可采取的整改措施比较有限。为此，建议结合工程建设进度，适时开展牵引变电所接地电阻、钢轨泄漏电导、N线阻抗等参数测试，根据测试结果提前制定合理的工程措施。