基于PCA-Shapley值的地铁盾构施工风险灰色聚类评价

赵 辉，马胜彬，卜泽慧

(青岛理工大学管理工程学院，青岛 266520)

引言

在我国城市化进程高速发展的背景下，城市人口急剧增加、建设用地逐渐减少，现有市政道路布局已无法满足人们的出行需求，而地铁的发展能够有效解决该类问题，成为当前的热门基础设施建设。在地铁施工中，盾构法已成为必不可少的施工工法，但盾构法施工过程中，往往受限于地下复杂的地质条件和地上交错的建筑物群，致使潜在的施工风险因素众多、施工难度加大。因此，科学合理的地铁盾构施工风险评价将有助于地铁建设的进一步发展。

近年来，随着社会对城市轨道交通建设的迫切需要，越来越多的学者针对地铁盾构施工风险展开研究。Tonon 等[1]将模糊理论和随机理论相结合，进行了隧道施工风险决策研究；黄震等先后提出通过云理论[2]和模糊-证据理论[3]解决盾构施工风险评估过程中的随机性和模糊性，均得到佛山-东莞区间隧道盾构施工风险等级为3级；宗秋雷等[4]通过引入C-OWA算子进行风险指标赋权，并运用梯形模糊数集结专家语义信息进行风险评估，得到深圳地铁12号线某区间各项指标的风险等级；洪文霞等[5]通过将DEMATEL和ANP法相结合对风险指标进行主客观组合赋权，并引入vague集法进一步对邻近建筑物条件下的地铁盾构施工风险进行评价；贾剑青等[6]采用AHP法和多级模糊综合评价法得到下穿黄河隧道风险指标集中在中等风险和严重风险两个等级上；李蒙[7]等通过EFA-SEM法得到盾构施工中盾构机进、出洞安全风险最大。分析上述文献中所提及的理论和方法不难发现，地铁盾构施工风险评价指标体系尚未形成统一标准，在评价方法的选择上大多都考虑了风险因素的模糊性，但却很少有考虑到指标的灰色性和指标间的组合对评价目标的影响，忽略了指标间的关联性。

鉴于此，本文构建了基于PCA-Shapley值的地铁盾构施工风险灰色聚类评估模型。首先通过主成分分析法(PCA)对风险因素集进行降维处理，得到更为客观的风险评价指标体系；然后采用Shapley值对指标进行赋权，有效解决了指标间的关联性，其非可加测度原则更好地反映了人脑思维，充分表达了各个指标间的组合影响；最后结合灰色白化权函数，解决了传统方法在进行风险评价时由于部分指标信息缺失造成的评估结果失真问题。据此建立的评估模型更加科学、合理，且计算效率也较高。

1 地铁盾构施工风险评价指标体系的构建

1.1 地铁盾构施工风险影响因素集

地铁盾构法施工程序较为复杂，涉及到人理、事理和物理的各个方面，因此在地铁盾构施工过程中各方面都存在潜在风险，在进行风险评价前需要建立一套完整的风险指标体系。现有研究中，DING等[8]对地铁施工风险的定义进一步阐释为“地铁施工过程中可能对经济、环境、人身、工期等造成影响的潜在不确定性”，明确了4个主要指标要素；周前国等[9]依照网络层次结构原理将风险指标划分为人的行为、物的状态、环境条件、管理缺陷和施工技术5个方面；覃晓萍[10]从盾构施工原理角度以施工工序为线索，构建了包括施工准备、修建始发井、盾构机拼装等阶段组成的指标体系；郭隆彪[11]对盾构施工安全进行问题梳理，将指标体系归纳为人员、机械设备、施工材料、施工技术和环境5方面因素；吴宗华[12]通过WBS-RBS法将盾构施工分为4个阶段，并从“机、法、环”三方面对施工风险进行分解等；其他学者[13-18]也从类似角度就地铁盾构施工风险因素进行了分析归纳。为了更加全面的筛选风险因素，依据国家现行的地铁工程施工安全评价标准，结合相关的实际工作经验，参考地铁盾构施工风险方面的上述研究，采用德尔菲法进一步调研分析，得到初步的地铁盾构施工风险影响因素集(表1)。

表1 地铁盾构施工风险影响因素集

1.2 数据收集与处理

邀请30位地铁施工从业者和相关专家对上节梳理的因素影响程度进行赋分，专家背景信息见表2。

表2 专家组成员背景信息

赋分采用十分值，通过专家意见征集，将指标影响程度评分表划分为低、中、高、很高4个等级(表3)，赋分结果作为原始数据矩阵。

表3 影响程度评分

1.3 主成分分析

采用Matlab软件进一步处理专家赋分得到的原始数据矩阵，得到主成分分析中的重要数据值(表4)。特征值越大说明代表性越强，因此主要保留特征值>1的主成分，此时方差累计贡献率86.8%，已涵盖了绝大部分信息。

表4 特征值、方差贡献率、累计方差贡献率

1.4 影响因素降维分析

由Matlab软件得到相关系数矩阵的特征向量(表5)，进一步分析主成分表达式Zg=ug1d1+ug2d2+…+ugpdp可知，某一因素对某个主成分相关系数绝对值越大，说明该因素对主成分的影响程度越高，据此可以进一步对影响因素进行再分类：

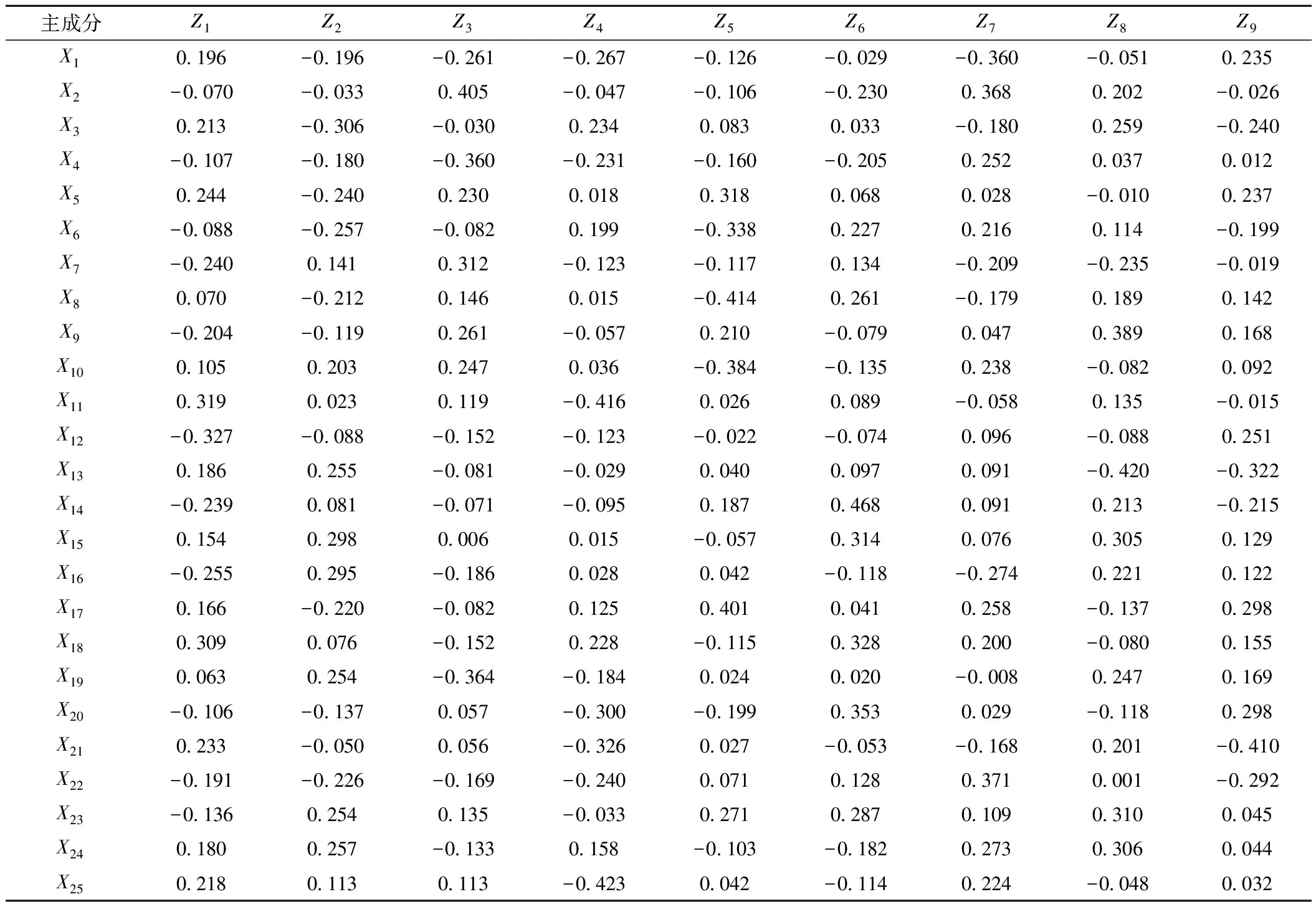
表5 相关系数矩阵R特征向量

主成分Z1中，X11、X12、X18的3个相关系数的绝对值较大，分别为0.319、0.327、0.309，因此X11、X12、X18可作为主成分Z1的主要指标，反映了关于泥浆处理方面的风险；以此类推，X3、X16可以表示主成分Z2，反映了施工工艺和材料的风险；X2、X4、X7、X19表示Z3，反映了施工操作方面的风险；X11、X20、X21、X25表示Z4，反映的是施工技术方面的风险；X5、X6、X8、X10、X17表示Z5，反映了人为因素和组织管理方面的风险；X14、X15、X18、X20表示Z6，反映了施工设备和技术方面的风险；X1、X2、X22表示Z7，反映了设备选型和操作问题；X9、X13、X15、X23、X24表示Z8，反映了施工环境风险；X13、X21表示Z9，反映了管片运输和拼装风险。

通过上文主成分分析，并结合工程实际情况，再将各主成分合并归类，Z1、Z6、Z7和Z9为设备和材料风险，记为A1；Z2、Z3、Z4为施工技术风险，记为A2；Z5为人的风险，记为A3；Z8为施工环境风险，记为A4。根据指标体系构建的合理性、全面性、代表性和独立性等原则，对相关指标进一步调整，得到表6。

表6 地铁盾构施工风险评价指标体系

2 指标权重的确定

地铁盾构施工风险指标涉及到人、事、物的各个方面，在进行风险评估前首先要明确各个指标对目标的影响程度，因此科学合理的赋权方法将使评价结果更加可靠。首先要明确的是，无论是因素层中设备和材料风险等4个因素之间，还是指标层中各个指标之间并非独立的，相互之间都存在一定的关联性，这种关联性会对目标产生或多或少的影响，而传统的熵权法、层次分析法等都以指标个体独立为前提，无法准确反映指标组合关联影响。

由美国学者Shapley[19]提出的Shapley值法在处理地铁盾构施工风险指标关联性中体现出较强的优势，该方法认为单个风险指标对施工目标的影响程度的简单线性相加并不能反映综合作用效果，这种非可加测度性所体现出来的是以指标间非线性的相互作用关系来表达多指标对目标的综合作用，据此分配指标权重更加合理，具体赋权步骤如下：

集合N={1，2，…，n}表示地铁盾构施工风险指标集，指标之间的组合集合表示为[N，V(S)]，指标之间的组合影响值表示为V(S)，s是n个指标的任意组合。

(1)确定各个指标所有组合形式的影响值大小，指标存在关联性时添加系数1.2，指标独立时添加系数1：

(1)

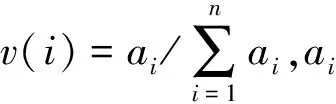
(2)确定指标权重ωi

ωi=shi(N，V)=

(2)

其中，s为评价指标子集S中评价指标的个数；S/i为评价指标子集S减去i元素的剩余组合。

3 地铁盾构施工风险灰色聚类模型的构建

3.1 地铁盾构施工风险的测度界定

地铁盾构施工风险评价中，其施工过程复杂性决定了影响施工的潜在风险因素众多，评价信息更为庞大，传统的评价方法很容易导致信息失真。对于地铁盾构施工风险程度的表述本身是一个定性化的灰概念，将“风险”科学定量处理才能进一步进行风险评价。根据实际经验对地铁盾构施工风险等级进行合理界定，得到地铁盾构施工风险评价测度，见表7。

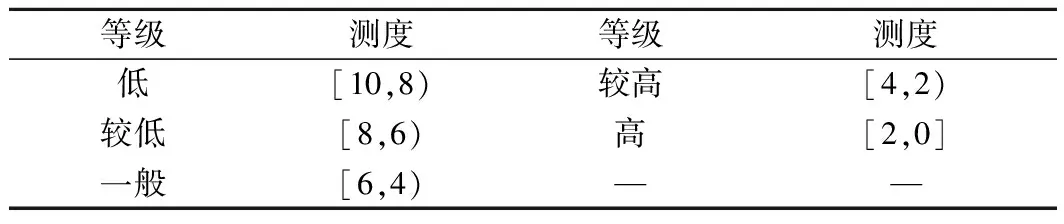
表7 地铁盾构施工风险评价测度

3.2 灰类及对应白化权函数的确定

灰类数可以用来衡量地铁盾构施工风险的类别，通过中心点向量原则，由表7可以分别确定灰类“低”对应的灰类中心点为9，“较低”对应7，“一般”对应5，“较高”对应3，“高”对应1。为了更好地表达每个指标数据的灰类隶属情况，主要参考了刘思峰[20]在灰色系统理论中提出的中心点三角白化权函数(表8)。

表8 灰类和对应的白化权函数

3.3 风险评价过程

步骤1：确定原始数据矩阵。首先邀请实际工程中从事地铁盾构施工环节的工作人员和专家组成风险评估小组，依照表6的赋分标准分别对上节指标体系中各项指标Aij的风险状况进行打分，最终得到原始数据矩阵Di=[dijk]s×p，其中，s为指标个数，p为专家人数。

(3)

步骤3：确定聚类评价矩阵Z，将指标权重和步骤2中确定的矩阵R相乘，得到指标层的评价值。

Z=ωi×Ri

(4)

由于存在因素层和指标层两级指标，首先将各个因素层综合评价矩阵表示为Z0=[Z1，Z2，…，Zn]T，通过聚类评价得到因素层的综合聚类评价向量

M=ω0×Z0=[M1，M1，…，Mn]

(5)

步骤4：单值化处理确定综合评价值W。通过综合聚类评价向量M和灰色测度阈值U合成得到综合评价值W=M×U，可以有效弥补最大隶属度原则在确定灰类时丢失信息而导致的结果偏差，据此对地铁盾构施工风险进行的评价更加合理可行。

4 实证分析

以青岛地铁1号线“安安”区间隧道为例(见图1)进行实证分析。青岛地铁1号线全长59.95 km，整段线路连通了青岛主城区和西海岸新区，穿越了青岛胶州湾。其中西海岸新区城内的“安安”区间(安子东站—安子站)左线全长940.54 m，最小平面曲线半径约500 m，“安安”区间隧道穿过雨水暗渠，地下水位约3.6 m，沿线穿越建筑物众多，地下管线分布极其复杂，具有线路超长、施工条件和工法复杂等特点。现邀请实际参与青岛地铁1号线设计施工的7位专家组成风险评估小组，针对地铁1号线“安安”区间隧道盾构施工风险进行评价。

图1 青岛地铁1号线线路示意(部分)

4.1 风险指标权重的确定

(1)7位专家分别针对设备和材料风险、施工技术风险、人的风险和施工环境风险4个方面15个指标的重要程度进行打分，由于篇幅原因，主要以人的风险A3为例进行演算，打分情况见表9。

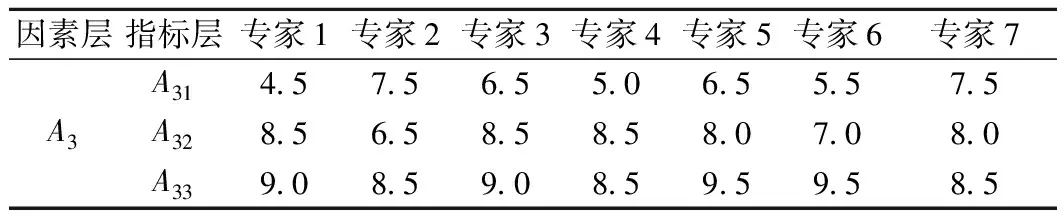
表9 风险指标权重打分

(2)由公式(1)计算得到各个风险指标组合对目标的影响程度大小，如表10所示。

表10 风险指标组合影响值

(3)根据表10数据，由公式(2)计算出各项风险指标的权重，限于篇幅仅展示指标A31的计算步骤

ω1=sh1(N，V)=

(0.733-0.343+0.789-0.389)+

因素层指标A1、A2、A3和A4的权重及指标层15个风险指标权重计算过程同上，结果如下：

w0=(0.185，0.252，0.238，0.325)；

w1=(0.312，0.201，0.153，0.136，0.198)；

w2=(0.256，0.195，0.280，0.269)；

w3=(0.262，0.343，0.395)；

w4=(0.425，0.276，0.299)。

4.2 盾构施工风险灰色聚类评价

(1)由评估小组参照表6对15个风险指标的风险程度分别打分，最终得到原始打分数据矩阵A1～A4

(2)由表8的计算规则确定灰色聚类权矩阵R1～R4

(3)由公式(4)将Shapley值赋权得到的权重向量与灰色聚类权矩阵相乘，计算得到综合评价矩阵Z

Z=ωi×Ri=

(4)由式(5)确定综合评价向量：M=ω0×Z0=[0.308，0.337，0.262，0.094，0.000]；

(5)结果分析。将综合评价向量M与灰色测度阈值U=(9，7，5，3，1)进行合成，单值化处理得到盾构施工风险综合评价值W=M×U=6.715，由测度表7易知，青岛地铁1号线“安安”区间隧道盾构施工风险等级为“较低”，在可接受范围内。进一步分析设备和材料风险、施工技术风险、人的风险和施工环境风险4个方面各自的评价向量可以得到各方面的综合评价值：W1=7.307，W2=7.241，W3=7.126，W4=5.668，盾构施工风险等级排序为施工环境风险>人的风险>施工技术风险>设备和材料风险，施工环境风险为“一般”水平，其中，地下地质条件不良、地下管线老化、地面沉降风险均较高。

结合风险评价结果，从“安安”区间段实际工程情况来看，该区间位于城市较繁华地段，地上建筑物众多，地下管线排布繁多，且地质较为复杂。安子东站作为盾构起点，距海边约200 m，地下水位为地面下3.6 m，地面沉降风险容易造成建筑物的沉降，甚至地下管线破裂，诸多复杂地质因素给施工带来了诸多风险。对此，相关单位和部门需要做大量的前期勘测工作，召开多次会议，对施工方案进行探讨、敲定。为保证施工安全进行，项目成员也需进行大量的前期管理和技术培训，对盾构机的最佳掘进参数和注浆配比进一步优化，严格控制管片等材料质量以及规范管片运输和拼装过程中的技术操作，解决近海富水复杂地层管片上浮及盾构机在软弱地层中掘进时盾体滚动等技术难题，尽可能降低相关风险。

5 结论

为对地铁盾构施工风险进行科学评价，构建了基于PCA-Shapley值的地铁盾构施工风险灰色聚类评价模型。主要结论如下。

(1)首先识别出具体的风险要素集，通过主成分分析法对25个风险要素进行降维处理，进一步归纳和完善风险指标，从设备和材料风险、施工技术风险、人的风险和施工环境风险4个方面构建评价指标体系，克服了指标选取的主观性。

(2)针对地铁盾构施工风险的指标关联性和灰色性，分别通过Shapley值法赋权和灰色聚类法进行风险评价，有效解决了部分指标信息不完整造成的评价结果失真。

(3)以青岛地铁1号线“安安”区间隧道为例进行演算，结果显示该线路盾构施工风险等级为“良好”，其中“施工环境风险”为“一般”，是施工过程中面临的主要风险，项目部需要针对各项指标的风险情况有针对性地采取相应措施，更好地保障盾构施工的安全性。

在未来的研究中，将通过更加科学的方法进一步挖掘指标数据，剖析每个风险指标对目标的具体影响，从而为地铁盾构施工做足准备，有针对性地进行精细化风险管理。