基于混合效应的湖北杉木冠长率模型
2021-03-24杜超群赵小涛肖志明
袁 慧,杜超群,赵小涛,肖志明,赵 虎
(1湖北省林业科学研究院,武汉430075;2阳新县自然资源和规划局,湖北阳新435200;3阳新县自然资源和规划局龙港自然资源所,湖北阳新435200)
0 引言
树冠是树木自身进行同化作用、异化作用、水循环等生理过程的重要场所,直接影响着树木的生长变化[1]、地上部分器官的垂直分布、同化器官和非同化器官的空间分配,又影响树木截获光照的程度,进而影响树木的能量交换和有机物的积累[2]。树木的活枝条对净光合作用具有积极贡献[3]。
冠长率(crown ratio,CR)是活树冠长度与树高的比值,往往用来预测树木或森林的生长和收获量,是一种无量纲的测度[4],是研究树冠结构非常重要的指标之一。冠长率可以反映树木活力、林木质量、林分密度和竞争的影响[5-6],也是部分经济树种一个很重要的特征量[7],同时对树木局部修枝也有指导作用[8]。有研究结果表明,冠长率影响树木的生长。欧建德等[9]对南方红豆杉进行修枝处理,发现当修枝后冠长率降低14%时,胸径、树高、材积和胸高形数均显著增加。袁从军等[10]研究黔中喀斯特次生林中多个树种冠型特征,得出冠长可以解释胸径和树高的0.64~0.88。
冠长率或树冠高度往往应用线性或非线性异速生长方程,把树木及立地特征因子作为模型回归变量进行拟合[11]。Ward采用多水平线性模型构建红橡树冠长率[12],分析了不同林龄冠长率差异。Jari利用非线性模型研究芬兰地区间伐对樟子松冠长率的影响[11],结果显示间伐强度和间伐后持续的时间对冠长率影响较大。与线性回归模型不同,由于模型固有结构,大多数非线性冠长率模型的预估值为0~1,能够得到合理的预估结果[13]。非线性模型应用较广泛,其中Logistics方程被应用于很多研究中。Hasenauer等[14]研究了奥地利多个树种的冠长率模型,分析了5000多个固定样地中42000多株树木的数据,利用Logistics方程进行非线性拟合,把树木大小特征量、林分密度和立地因子组合作为模型变量,得出树木大小因子和竞争因子对林分主要树种冠长率的影响程度最大,达到17%~41%的解释程度,而立地因子影响程度较小,不足10%。符利勇等[15]研究东北地区蒙古栎冠长率,构建了多水平非线性混合效应模型,结果显示,立地和树木大小因子对模型的预估作用最大,其中平均胸径、优势木树高和优势木胸径变量是重要的模型预测变量。
湖北具有大面积的杉木人工林,分布于鄂东南、鄂西和鄂西北等地,各地的环境因子差异较大,对杉木人工林的生长影响也较大。本研究通过在湖北省多个杉木栽植地区设立临时标准样地,利用解析木测量数据拟合杉木冠长率,分析单木因子、林分因子和环境因子对冠长率的影响,预测冠长率变化,旨在为杉木人工林合理经营提供参考。
1 材料与方法
1.1 研究区概况
湖北省地处中国长江中游,东经108°21′42″—116°07′50″、北纬 29°01′53″—33°6′47″。全省总面积18.59万km2,其中东西跨度740 km、南北距离470 km。地势三面高、中间低,向南敞开,北部有不完整盆地,整体处于中国地势第二级阶梯向第三级阶梯过渡地带,呈北西向南东走向。最高峰为神农架神农顶,海拔3105 m,平原区海拔约为20~100 m。年均气温15~17℃,无霜期230~300天,年均降水量800~1600 mm。除高山地区外,大部分为亚热带季风性湿润气候。
1.2 研究方法
1.2.1 数据收集与整理 以2016年6月—2017年10月杉木人工林标准地调查数据为基础,样地主要分布在湖北黄石、咸宁、襄阳、宣恩等杉木集中栽植地区。选择具有代表性、不同立地条件且生长良好的杉木林分设置临时标准样地,样地面积600 m2(20 m×30 m)。记录样地海拔、坡度等立地信息,样地内每木检尺,起测胸径为5 cm,分别测量树高、胸径、冠幅和活枝下高等,使用超声波测高器测量树高及枝下高。每个样地内选择3株树干通直、长势良好的平均木和1株优势木,解析木伐倒后使用皮尺测量树高、冠幅及冠长,伐株按2 m区分段获取解析木圆盘。共设立标准样地181块,伐取解析木715株,按照总样本量的30%做检验样本,其中建模数据500株、检验数据215株。参与建模与检验的数据基本统计信息见表1。
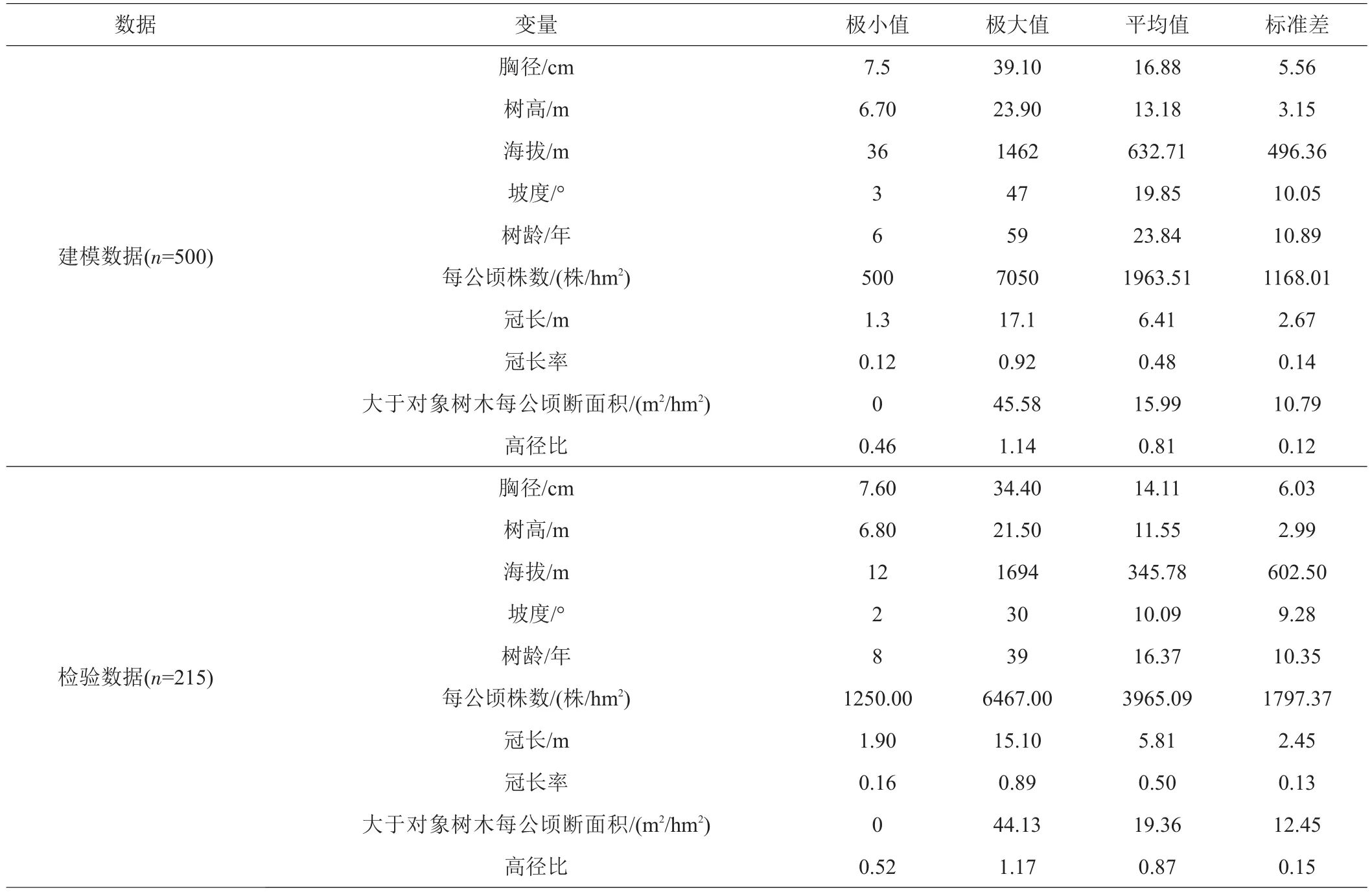
表1 样地和解析木基本信息统计
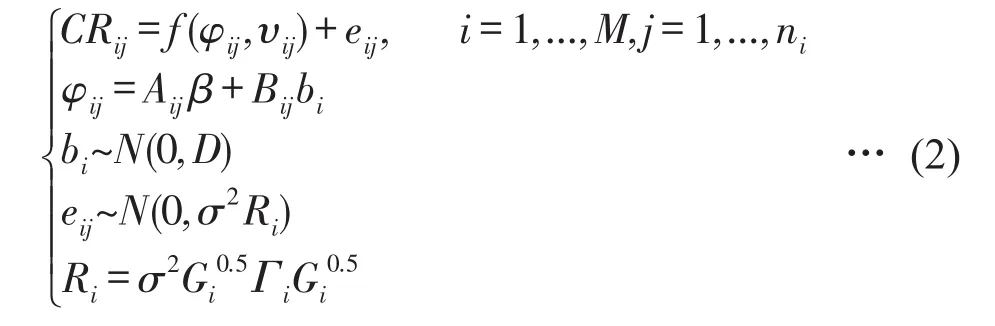
1.2.2 冠长率模型的构建 按照冠长率的定义,冠长率的范围为0~1,0表示没有树冠或者死亡,1表示全树冠。由于Logistics方程受到[0,1]范围的限制,可以很好地解释冠长率的变化趋势,已有许多研究应用Logistics方程来描述针叶和阔叶树种的冠长率[15-20],基础方程如式(1)。

式中,CR为冠长率,β×X表示一个参数为β、独立变量为X的函数,e为自然常数。变量X通常由代表林木大小、竞争变量和立地条件等变量因子构成。
本研究冠长率相关变量中的林木大小因子主要包括树高、胸径和高径比,树木竞争因子变量包括每公顷株数、大于对象树木断面积,立地条件因子包括样地海拔、坡度。
在基础模型基础之上,考虑样地水平的随机效应对冠长率的影响,构建湖北人工杉木冠长率非线性混合效应模型。根据构建混合效应模型的一般步骤[21-22],首先确定模型的固定效应参数与随机效应参数,再确定用于解释不同样地内方差-协方差矩阵结构,最后确定方差和协方差的随机效应矩阵。非线性混合效应模型形式如式(2)。
式中,i、j分别代表第一水平和观测值,本研究仅考虑样地水平;CRij为第i个样地中第j株树冠长率的观测值;M为样地数量;ni为在第i个样地上的株数;f为含有参数向量φij和协变量向量υij的函数;β为p×1维固定效应参数向量,bi为带有方差-协防差矩阵D的q×1维随机效应向量;Aij和Bij为设计矩阵;eij为模型服从正态分布的误差项;σ2为方差;Ri为分组样地内的方差-协方差矩阵[24];D为随机效应的方差-协方差矩阵;Gi为描述方差异质性的对角矩阵;Γ为样地内误差的相关性结构。
将所有可能的参数组合均作为随机效应进行拟合,利用赤池信息准则(akaike information criteria,AIC)、贝叶斯信息准则(bayesian information criteria,BIC)和对数似然值(log likelihood,LL)统计指标对模型进行评价[15,22,24]。AIC、BIC值越小,对数似然值越大,模型拟合效果越好。分别选取含有不同个数参数效应的最优模型进行似然比检验(likelihood ratio test,LRT),最终选择参数较少且模型显著的作为最优模型。
利用广义正定矩阵和对角矩阵检验随机效应的方差-协方差矩阵,选择AIC、BIC小且对数似然值较大的矩阵形式。通过消除样地内测量值间的误差相关性和异方差问题确定组内方差-协方差结构,若观测数据是连续型的,则要考虑误差相关性。本研究中冠长率数据是一次调查,只需考虑异方差问题,采用指数函数及幂函数对模型进行矫正,并用AIC、BIC、对数似然值比较矫正效果,指数函数和幂函数形式如式(3)~(4)。
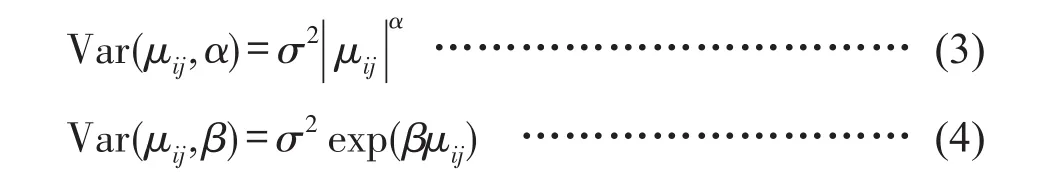
式中,μij为基于固定效应参数的预测值,α、β为指数函数和幂函数的参数。
模型拟合及检验除使用AIC、BIC、log-likelihood统计指标,还采用均方根误差(RMSE)、平均误差(Bias)和拟合精度(R2)指标。本研究中基础模型及非线性混合模型均采用R软件(3.6.1)中nlme程序包实现。
2 结果与分析
2.1 冠长率与林木及林分因子间相关性
冠长率是树冠长度与树木高度间比值。按照冠长率范围0~1,把(0,0.1]的冠长率划分为等级1,以此类推共划分为10个等级。本研究区杉木人工林平均冠长率为0.49,范围在0.1~0.9之间。由图1可以看出,冠长率总体呈正态分布,等级主要集中分布在4~7,占总体的85%。冠长率与林木及林分因子的相关性如表2所示,胸径和树高与冠长率呈显著正相关,而每公顷株数、大于对象木断面积、高径比与冠长率呈显著负相关,海拔、坡度和年龄因子对冠长率无显著影响,说明林木大小及竞争因子对冠长率影响较大,而立地因子影响较小。树木间竞争程度大抑制树冠的生长,致冠长率降低。

表2 冠长率与林木、林分因子的Person相关性分析
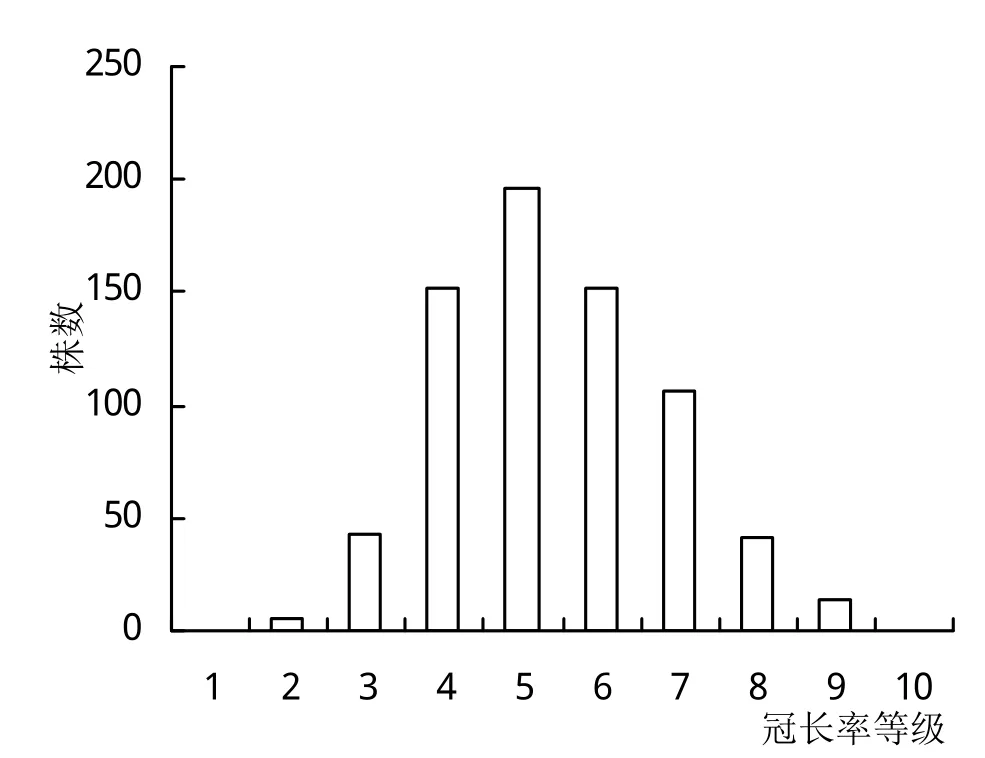
图1 冠长率等级分布
2.2 基础模型建立
根据冠长率与树木及林分因子的相关性分析,将相关性显著的DBH(胸径)、HT(树高)、SD(每公顷株数)、BAL(大于对象树木断面积)、HDR(高径比)因子引入到Logistics方程作为变量。因此,杉木冠长率模型的具体形式如式(5)。
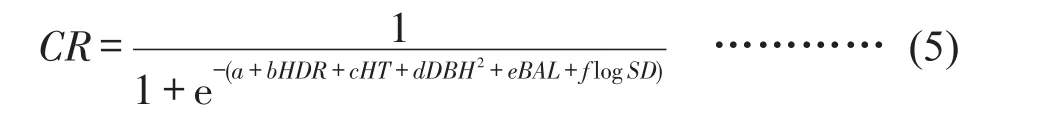
式中,a、b、c、d、e、f均为模型参数。使用R软件nlme程序包中nls函数,拟合得到a=1.055,b=-0.693,c=-0.056,d=0.001,e=-0.01,f=-0.121,模型决定系数R2为0.3231。
2.3 混合模型参数的确定
将模型所有参数及其组合形式(49种)作为随机效应进行拟合,由于模型参数较多,部分组合形式拟合无法收敛。对含有不同随机参数个数的随机效应模型分别选择1个最优的模型进行比较,结果如表3所示。

表3 基于样地效应的混合模型拟合结果
当模型没有随机参数时,AIC=-975.154,BIC=-867.5326。当随机参数增加1个最优参数a时,AIC(-1005.499)和BIC(-961.0544)的值减小。当增加2个随机参数a和f时,AIC(-1006.777)和BIC(-968.920)的值继续减小。当考虑其他随机参数组合时,增加3个随机参数b、c、e和4个随机参数a、b、c、e的AIC和BIC的值相较无参数均降低,但与1个参数a和2个参数a、f的结果比较却增大。似然比检验表明,无随机参数和1个参数a模型有显著不同(LRT=10.32,P=0.0221),参数a模型拟合和参数a和f模型拟合有显著不同(LRT=9.46,P=0.0314)。说明通过增加随机参数可以显著提高模型拟合精度。综上分析,选择含有随机参数a和f为最优混合模型。
2.4 方差-协方差矩阵的确定
确定混合模型样地间方差-协方差矩阵,对比广义正定矩阵和对角矩阵对混合模型拟合效果的影响。结果(表4)显示,广义正定矩阵的拟合效果较好,AIC(-1006.778)和BIC(-961.053)值小于对角矩阵,似然比检验表明两者差异显著(LRT=5.28,P=0.0216)。因此选择广义正定矩阵作为随机效应的方差-协方差矩阵形式。
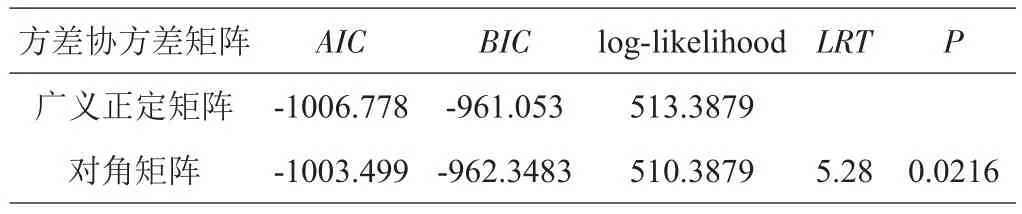
表4 基于随机参数效应不同方差协方差结构混合模型拟合结果
2.5 模型参数估计和独立样本检验
利用幂函数和指数函数来描述混合模型产生的异方差现象,拟合效果见表5。指数函数的AIC(-1015.075)和BIC(-964.7797)值小于幂函数,说明指数函数拟合效果较好,似然比检验也表明指数函数明显提高了模型拟合精度。
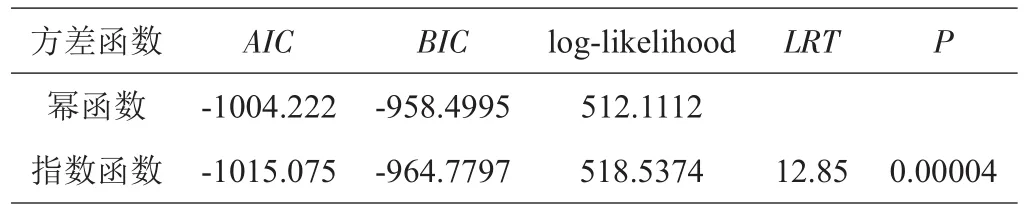
表5 基于不同方差函数混合效应模型拟合结果比较
混合效应模型采用指数函数拟合后,由模型的残差结果可知,残差分布范围明显减小(图2~3)。基础模型与混合模型的参数估计结果见表6。基础模型的Bias、RMSE、R2分别为-0.0862、0.1458、0.9190,混合模型Bias、RMSE、R2分别为-0.0095、0.1175、0.9475,可知混合模型拟合效果较好。
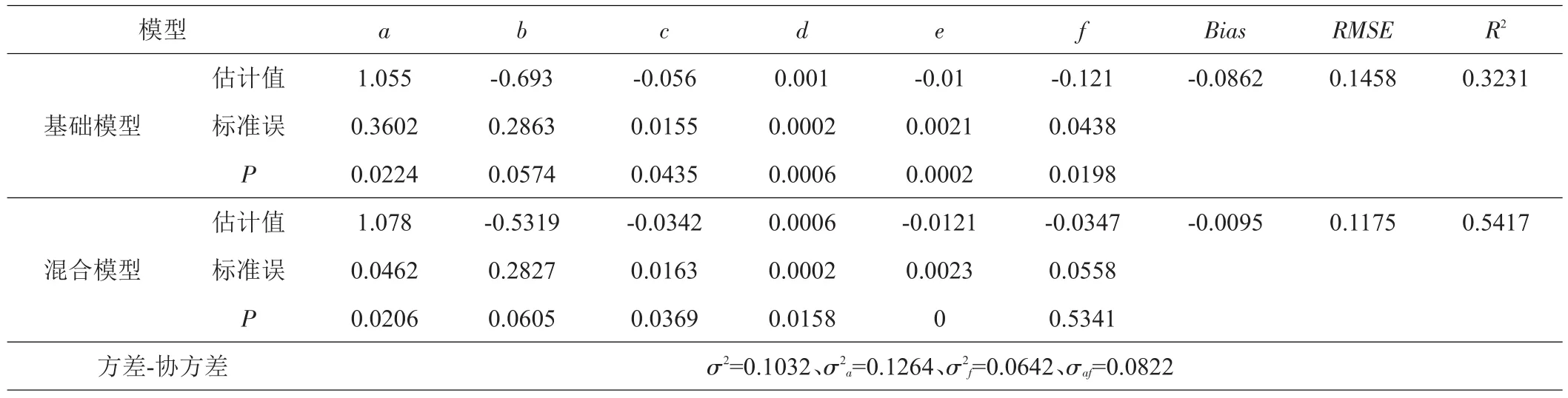
表6 基础模型与混合模型参数估计结果
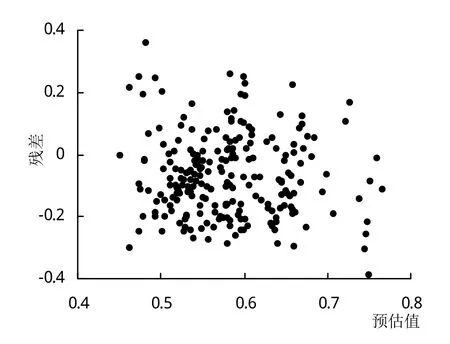
图2 基础模型预估值残差
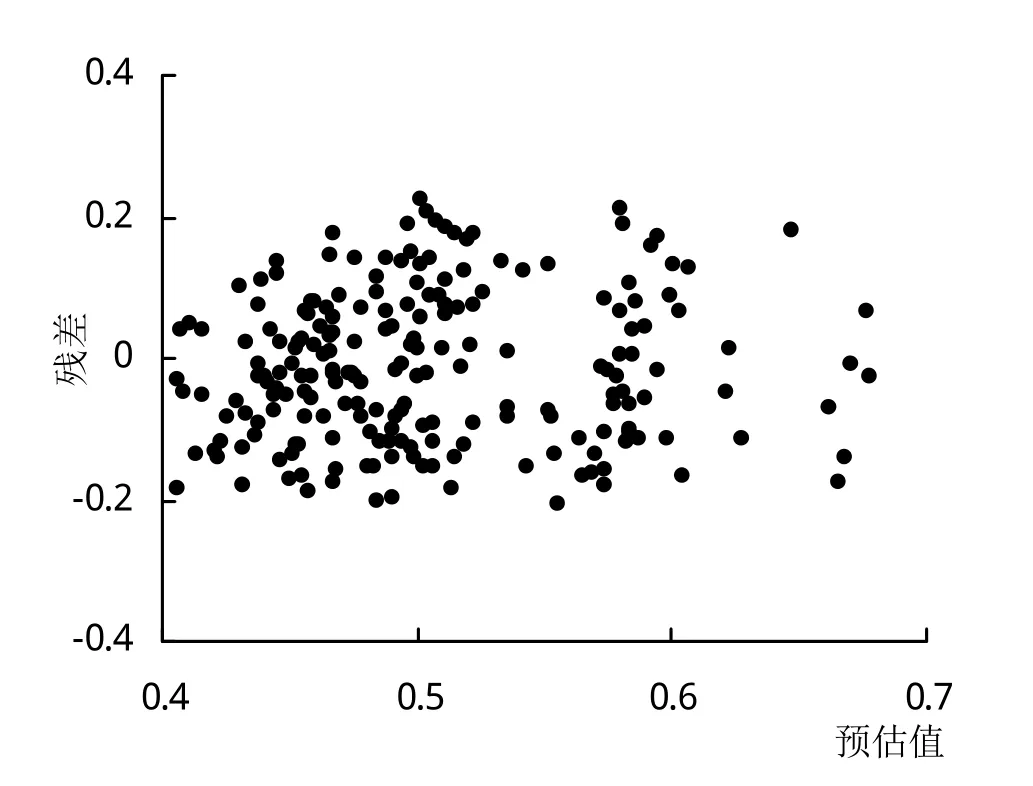
图3 混合模型预估值残差
混合模型应用独立样本进行检验,一般包括固定效应部分检验和随机效应部分检验。随机效应部分的检验需要二次抽样来计算随机参数值,固定效应部分检验相当于传统回归分析检验,即采用固定参数估计值,本研究只涉及固定效应部分检验。利用215株树木样本对基础模型及混合模型进行检验(表7),混合模型的检验精度大于基础模型,且均方根误差和平均误差均小于基础模型,因此混合模型拟合效果显著优于基础模型。

表7 基础模型和混合模型检验
3 结论与讨论
为保证树冠长度数据准确性,本研究所用树冠长度数据由样地调查中伐倒解析木实地测量得到。通过分析冠长率与林木及林分因子相关性,将相关性显著因子引入Logistics方程作为变量,并建立非线性混合效应模型。杉木冠长率主要集中在0.3~0.6范围内,占总样本量的85%。对混合模型所有参数及其组合形式均作为随机效应进行拟合,分析模型AIC、BIC值和似然比显著性检验,与无随机参数相比较,含有随机参数a、f的混合模型拟合效果最优。采用广义正定矩阵来确定样地间方差-协方差矩阵形式,利用指数函数来描述混合模型产生的异方差,最终得到混合模型参数。混合效应模型应用独立样本进行检验包括固定效应和随机效应检验,本研究采用固定效应参数估计值,即相当于传统回归分析检验,没有计算随机参数值和样地随机抽样检验。根据独立样本检验结果,混合模型相比基础模型的决定系数明显提高,均方根误差和平均误差均有所降低,残差范围也显著减小,综合表明非线性混合效应模型拟合效果优良。
从混合模型拟合参数可知,胸径变量参数值为正,每公顷株数、大于对象树木断面积和高径比的参数值为负,除树高变量参数外,其余变量参数结果与冠长率相关性分析结果吻合。结果显示,树高的增加导致冠长率的降低,这与Hailemariam等[16]研究加拿大哥伦比亚地区的阔叶树种冠长率结果一致;而郭孝玉等[20]研究长白落叶松冠长率的结果显示,树高与冠长无显著相关性,这说明对于不同地区、不同树种,同一因子对冠长率的影响结果也有差别。胸径是一个重要的树木生长变化的变量,通常用于解释林分结构、树木活力和竞争能力[15],本研究中胸径变量与冠长率显著正相关,混合模型参数也为正值,与卢军等[19]研究次生林部分树种冠长率结果一致;郭孝玉等[20]研究结果也得到类似的拟合结果,表明胸径指标与冠长率关系密切,是一个很重要的变量。竞争因子变量结果意味着林分密度增加、大于对象树木的林木竞争能力的增强,林木冠长率变小,说明树木周围环境竞争压力的增加会抑制树木本身树冠的生长,进而影响树干的发育。拟合的变量参数对模型具有一定解释意义。
立地因子的差异对不同树种冠长率影响也有所不同[15-16,19]。本研究中只涉及湖北省人工杉木,没有做研究区其他树种的对比分析,研究中立地因子(海拔、坡度)对冠长率无显著影响,可能与本研究中立地因子的类型和数据量较少有关,还无法有效反映立地的影响程度。
