模糊神经网络PID在提升机恒减速系统中的应用研究

王利栋，王 政

(1.大同煤矿集团有限责任公司同大科技研究院，山西 大同 037003；2.中国矿业大学机电工程学院，江苏 徐州 221116)

0 引 言

矿井提升机是一个复杂的非线性时变系统，不同的提升载荷对紧急制动下提升机制动性能有着较大的影响，而恒减速制动方式能够很好地保障紧急制动的安全性。当发生紧急情况时，恒减速制动通过改变盘闸压力值，可以使提升机以不变的减速度停车[1]。以上功能的实现，依赖于对控制策略的研究。

当前，提升机恒减速系统的控制策略仍然以PLC内置的PID控制为主[2]，但参数确定后便不可再进行微调，往往无法适应复杂的恒减速制动工况，更无法满足紧急制动情况下响应迅速，制动平稳的要求，在此基础上，有学者提出了模糊PID控制[3]，将离线的模糊规则与PID相结合，使参数可以在一定程度上进行微调，提高了控制精度，但无法针对整个提升过程，尤其是对突发状况做出更加合理的判断，仅仅是控制算法上的优化，且其性能过于依赖模糊规则的设定，因此，有学者提出了BP神经网络PID控制方法，将神经网络结构引入恒减速系统中，通过迭代训练反向优化权值与阈值[4]，从而动态地微调PID参数值，弥补了此前研究的不足。但恒减速控制系统多数以PLC作为控制器，PLC对神经网络的处理能力较弱，同时会占用其他安全策略的反应时间，增加了制动系统不确定风险。

本着使PID参数更加精确的原则，本文引入模糊神经网络PID算法，将离线的模糊规则与可反复迭代优化的BP神经网络相融合，既满足了可根据不同工况微调PID参数值的要求，又解决了PLC处理大量数据能力不足，影响整个安全策略可靠性的问题，并对恒减速装置的控制策略做进一步优化探究。

1 提升机恒减速制动系统的控制原理

恒减速制动是提升机紧急制动的一个重要制动方法，当实施恒减速制动时，可通过编程控制器实时获取提升机的减速度，通过与人机界面设定的减速度做减法得到减速度误差，将减速度误差与减速度误差变化率作为模糊神经网络控制器的输入。为使减速度的值在要求范围内，本文将模糊PID与BP神经网络相结合构建模糊神经网络PID控制器，将在实验条件下得到的数据集注入神经网络结构，通过不断地迭代更新，根据误差值反向修正权值与阈值，即改变语言值与模糊规则，完成神经元结构优化。 最终输出变化量ΔKp、ΔKi、ΔKd，并根据变化量调整PID值，输出相应的电液比例溢流阀的控制信号，调节盘式制动器内的油压，改变制动器作用于滚筒的制动力矩，使提升机减速度达到给定减速度允许的误差范围内直到停车。其控制原理图如图1所示。

图1 恒减速制动系统控制原理图

其中，恒减速系统的盘式制动器的制动原理图如图2所示。制动发生时，弹簧弹力大于油压，最终闸瓦与制动盘接触，通过摩擦力对卷筒进行制动。故活塞通过闸瓦压向制动盘的正压力N见式(1)。

N=F2-F1

(1)

式中：F1为压力油产生的作用力，N；F2为弹簧的作用力，N。

盘式制动器在制动盘上产生的制动力矩取决于正压力N的数值，计算公式见式(2)。

Mzh=2NμRmn

(2)

式中：Mzh为制动力矩，N·m；μ为闸瓦对制动盘的摩擦系数；Rm为制动盘制动半径，m；n为提升机制动器副数。

注：1-碟形弹簧；2-活塞；3-闸瓦；4-制动盘。

故通过调节进油口油压就可达到调节制动力矩的作用，不断调节制动力矩保持恒定减速度制动。

2 模糊神经网络控制器的搭建及实现方法

Matlab软件中的ANFIS工具箱是构建模糊神经网络控制器的主要工具，它能够对通过模糊PID获得的数据进行训练，构建出神经网络结构，得到隶属度函数和控制规则表[5-6]，并建立基于恒减速系统的二维模糊推理模型。

首先在Matlab软件中调用ANFISedit窗口。其次加载训练数据，由于恒减速系统是一个复杂的时变系统，对于每种可能出现的状况都要充分考虑在内，故采集不同的提升工况进行分析[7]，将实验条件下预先获取的每个情况中的减速度误差E、减速度误差变化率EC以及ΔKp、ΔKi、ΔKd注入到神经网络结构中，并随机划分训练集与测试集。最后对该样本进行人为设定训练次数即可。经过以上步骤后，就完成了利用训练数据建立模糊神经网络的过程。其中，将训练次数Epochs设置为1 000次，训练误差最终稳定在0.418 14。训练完毕，得到训练完成的神经网络结构模型，该模型的隶属度函数如图3和图4所示。

图3 偏差隶属度函数曲线

图4 偏差变化率隶属度函数曲线

本文使用查表法将模糊神经网络离线学习训练过的模糊PID控制算法应用到西门子的PLC中，即经过训练的模糊神经网络系统，可导出语言变量E和EC与输出ΔKp、ΔKi、ΔKd的离线赋值表，将得到的赋值表写入可编程控制器的全局数据块中，并以二维数组的形式存储调用。该方法更加符合对响应速度要求高的系统，成本低且改造更为方便。

当危险工况发生需紧急制动时，恒减速系统被激活，为保证减速度为恒定值，PLC调用E和EC与ΔKp、ΔKi、ΔKd的离线赋值表，在PLC中表现为二维数组组成的数据块，随后与相匹配的量化因子相乘得到实际的变化量；并将其与起始值运算后，得到实际PID值，通过此种方法的PID运算即可满足要求。

3 系统模型与仿真

控制器按上述方法搭建完成后，为了验证其可行性，本文采用AMESim和Simulink联合仿真[8]。该方式利用AMESim中提供的AMESim-Simulink接口把AMESim中的模型编译为Simulink模型支持的S函数，然后通过Simulink中的S-Function模块调用编译后产生的S函数，实现联合仿真。

恒减速制动系统在AMESim中搭建如图5所示的恒减速制动仿真模型。本系统将减速度与减速度误差变化率放在AMESim模型中运算，作为Simulink的输入接口，比例溢流阀的控制信号作为输出接口。

模型构建后，使用同煤四矿提升机的相关技术参数，对仿真模型的模块设置相应参数，见表1。其中，先导式比例溢流阀的型号采用ATOS的AGMO-REB-P-NP-010/210。

图5 AMESim中恒减速系统模型

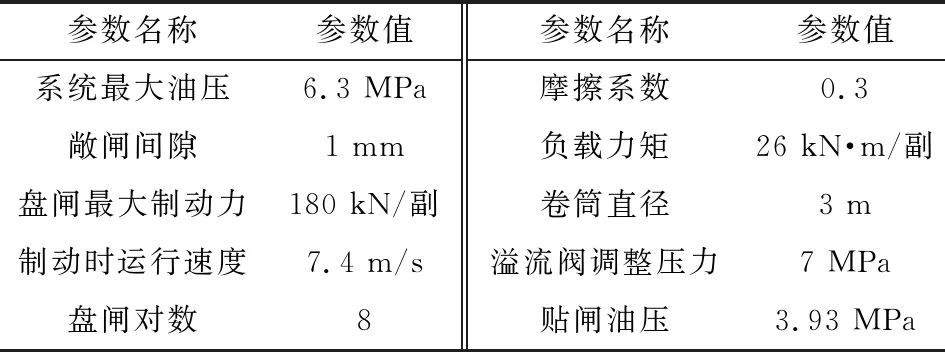
表1 提升机技术参数

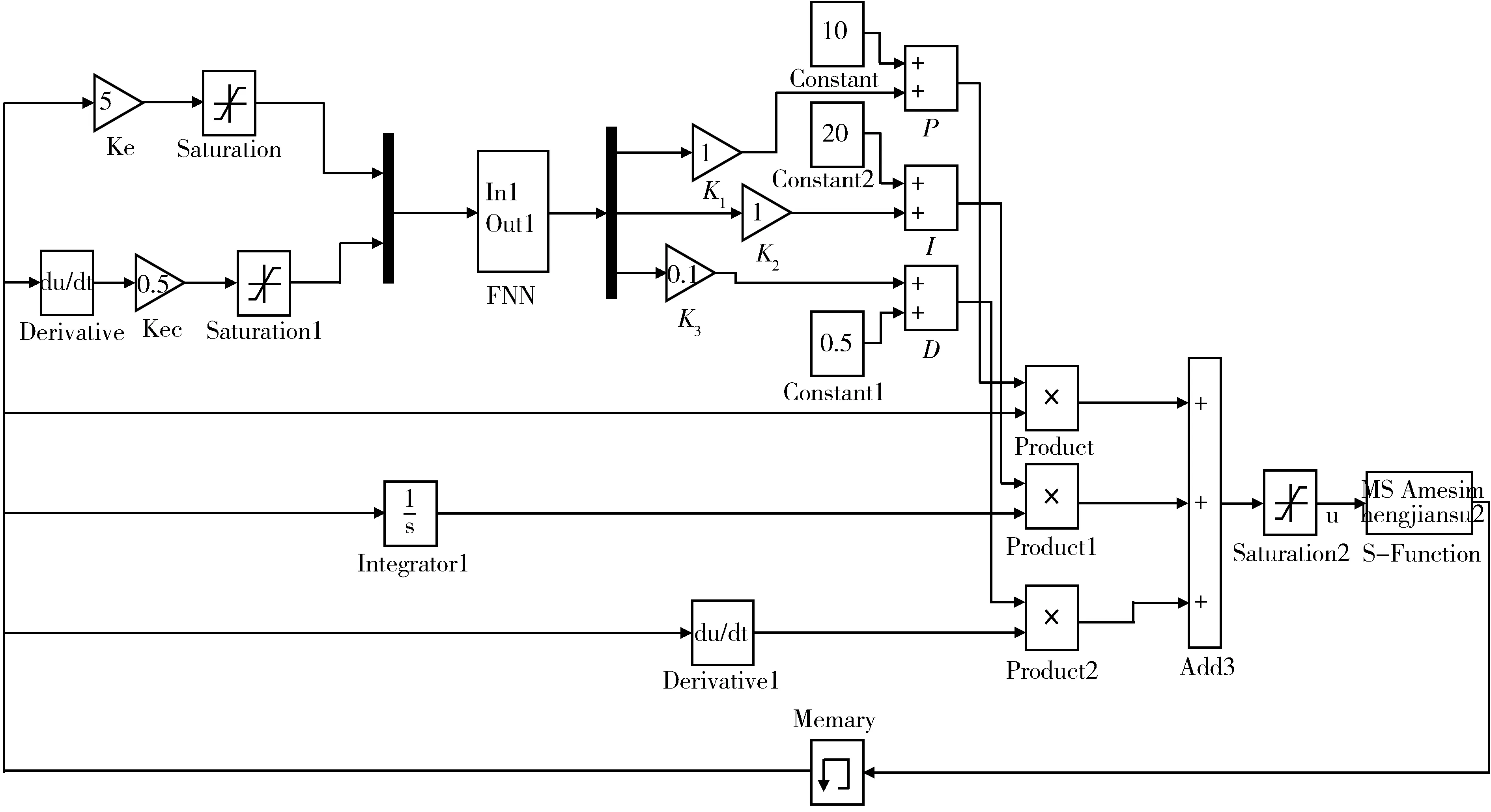
图6 Simulink中的仿真模型

图7 空载上提、下放时模糊PID与模糊神经网络PID控制效果

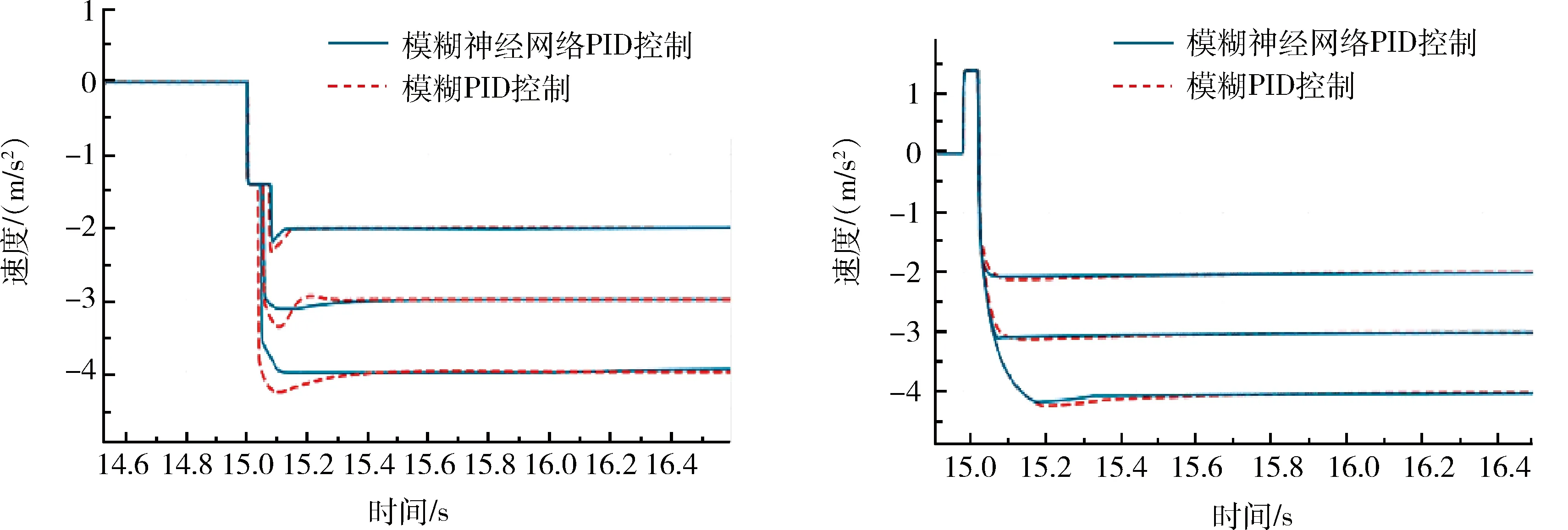
图8 重载上提、下放时模糊PID与模糊神经网络PID控制效果

依据控制系统的结构和原理，在Simulink中构建仿真模型如图6所示。K1、K2、K3分别表示ΔKp、ΔKi、ΔKd的比例系数；增益模块Ke、Ke表示E和EC的量化因子；FNN模块即为模糊控制模块[9]，将事先命名好的模糊控制器的文件名即“FNN”输入到该模块的命名栏里，既可完成模块与控制器的连接，模糊控制器的输入E和EC以及输出ΔKp、ΔKi、ΔKd的隶属度函数使用前面经神经网络训练好的隶属度函数；将AMESim中的恒减速液压模型进行封装，转化成Simulink可作为接口的S函数模块，即可完成液压系统的仿真。

根据《煤矿安全规程》规定，提升机安全制动的减速度不能超过5 m/s2。 为验证本文所探讨的控制策略，将减速度值设置为2，3，4，既满足了《煤矿安全规程》规定，也使减速度更具有代表性。 仿真不仅设定了不同的减速度，还综合考虑了不同的工况，如空载与重载情况下的提升与下放，4种工况下分别对两种控制算法进行对比分析，如图7和图8所示。

根据以上比对分析可以看出，当选用模糊神经网络PID作为该系统的控制算法时，在4种工况下制动到指定减速度的时间都有明显的减少，且都可以满足在接收到安全回路掉电信号后的0.8 s内必须达到恒定的减速度的行业要求,且在调节的过程中减速度超调量更小，稳态精度更高。

4 结 语

本文针对恒减速装置的PID算法进行了进一步的研究，引入了模糊神经网络PID。通过在4种不同工况下的仿真，并与模糊PID控制算法进行比较。 结果表明：①该方案在所示三种减速度中减速度的超调量更小，且相比于模糊PID控制，稳态精度更高，效果更好；②对于减速度的响应时间更短，且均满足0.8 s内达到恒定减速的要求，相比于模糊PID控制，响应更快，对恒减速系统的优化更好。