基于磁悬浮轴承的改进PID控制分析

吴哲昊 傅妙灿 王雩语 李旭

重庆理工大学电气与电子工程学院，中国·重庆 400050

1 引言

对于磁悬浮轴承来讲，传统PID 控制，往往是以中心点为控制目标参考量，故净差量也是基于中心点，实际上这样是存在运动学上的问题[1]。例如，在控制重力方向时，径向轴承上端给力克服重力，如果想让轴承到达中心点，应考虑在其还未到达中心点前就撤销上端的力，让转子凭借惯性到达中心点。但传统PID 控制显然没有考虑到这个问题，使其到达中心点后才撤销上端的力，这样实际转子已经偏离中心点往上了，很容易造成转子的碰壁，这是在转子高速运转中所不允许的。于是论文在进行PID 控制时，净差量选取的是传统PID 净差量的k（k ＜1）倍，k 值选取是关键，因为随着k 值的不同，会导致转子质心在中心点附近不同程度的波动，所以绘制不同k 值下转子质心的波动图，找出最佳k 值是关键[3-4]。

2 K 值选取测试

根据前文改进PID 控制策略，对实物进行了测试，通过纪录显示屏上传感器的实时数据，描绘了在不同k 值下转子轴心运动轨迹图，并记录下转子的运动状态。在进行多次k的调试后，选取了k=0.5 和k=0.429 时，前轴位移传感器的示数（以上端和左端示数为基准），每组纪录40 组数据，通过推算得到相应的轴心的坐标，据此绘制轴心轨迹图。如图1（a）、（b）所示分别为k=0.5 与k=0.429 时，前轴轴心轨迹图。

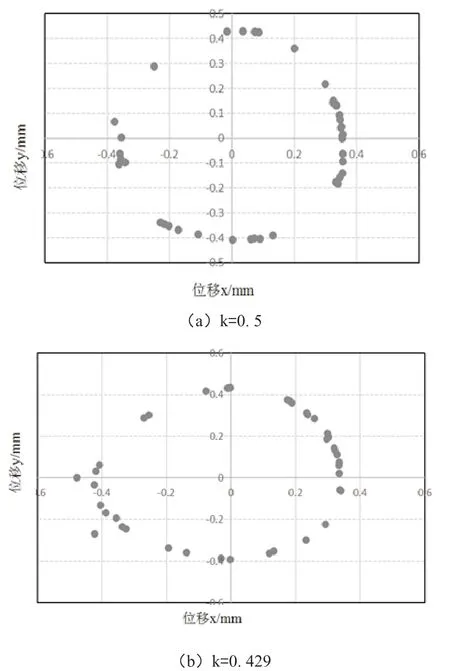
图1 前轴轴心轨迹图

由此可见，k=0.429 时，转子轴心轨迹更形似圆形，更聚拢中心点。在实验过程中发现，k=0.5 时，转子悬浮过程中存在明显的不平衡振动，k=0.429时这种振动有明显的减小。同时通过多次数据比对，当k ＞0.5 时，转子偏向上端，k ＜0.5时，转子偏向下端，但在0.429 时，悬浮最稳定。

从前轴轴心轨迹图可以看出，轴心的轨迹可以看成一个半径为0.4 的圆，由于轴承最大气隙为0.6mm，所以转子基本实现了与磁悬浮轴承的隔离，当转子高速旋转起来，由于离心力的作用，转子轴心的轨迹实际会更聚集于中心点[3]。

3 改进PID 控制测试

在选定参数k 前提下，使用改进PID 对系统进行控制，测试在不同PID 之下转子运动情况，通过串口输出每个控制周期上下端气隙的实时数据，选择上下端气隙之差作为衡量标准，当其为负值时表明转子在中心点以下，正值表明在中心点上方，为0 时转子处于中心点[5-7]。如图2（a）、（b）、（c）、（d）所示分别为不同PID 参数下转子的运动轨迹，横坐标为控制的周期，纵坐标为上下端气隙之差。

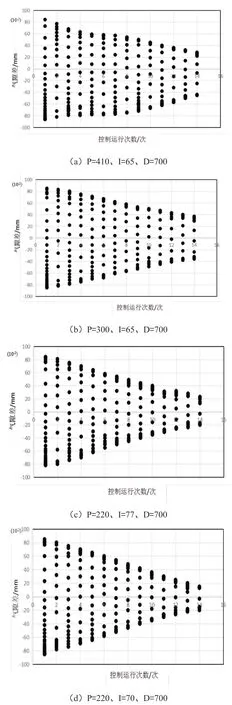
图2 不同PID 参数下转子运动轨迹

从转子的轨迹图来看，改进PID 控制是起到控制效果的，在后面的控制周期中转子在竖直方向上上下的幅度减小，最终在中心点附近运动[5]。在实测过程中发现参数P 对控制效果起着明显的作用，在P=410 控制下，转子运动的幅度很大，具有碰壁的风险，于是将P 值减小，当P=300 时，转子运动幅度明显减小，最终发现P=220 时，效果最好，小于220，转子无法启动。目前当I 值在70 时，系统较稳定[7-9]。

4 结语

通过测试发现：不同k 值，转子质心在中心点附近有不同程度的波动，通过不同k 值波动图对比，得出当k=0.429时，转子悬浮最稳定，转子轴心轨迹更聚集于中心点。此外，在选定k 值的情况下，改变PID 参数，经过对比发现在P=220、I=70、D=700 时，控制效果最好，系统也较稳定。