岩层移动内外“类双曲线”整体模型研究

左建平,吴根水,孙运江,于美鲁

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083; 2.中国矿业大学(北京) 采矿岩石力学基础科学研究中心，北京 100083)

长期以来，岩层移动与开采地表沉降普遍被划分为2个较为独立的学科。岩层移动主要关注采矿引起的岩层破断力学行为(岩层内部瓦斯、水等运移变化、采场和巷道空间的稳定等)。而地表沉降相关研究则侧重在地表沉陷所带来一系列环境、设施、生活和生态等的影响。然而岩层移动与地表沉降之间存在联系，开采必然引起上覆岩层发生运动，其本质是力学现象，影响和制约安全和生态环境[1]。在20世纪80年代早期，钱鸣高院士首先将上覆破断岩块视为构件单元，用结构力学方法获得了基本顶破断岩块相互铰接“砌体梁”结构力学模型以及稳定条件[2-4]。到了20世纪90年代中期，随着对岩层控制科学研究的不断深入，人们开始逐渐意识到开采对地表与地下环境产生的影响。因此，钱鸣高院士及其团队进一步提出岩层控制关键层理论。以关键层作为岩层移动研究的主体，用力学方法解释岩体采动后的结构形态、应力场和裂隙场的改变。由此对采场矿压、开采沉陷、采动岩体水与瓦斯运移有了较为统一的认识和完整的力学描述[5-6]。

岩层冒落与裂隙带的形态与大小为岩层移动与地表沉降提供了条件。掌握冒落拱、裂隙拱移动规律与形态的变化对煤层群上行开采、强含水层或承压水下采煤、下保护层开采等等的安全开采距离评价具有重要指导意义。近年来，已有大量国内外学者对岩层破断规律与状态进行了一系列理论与试验研究。如FENG和WANG[7]认为不论是近水平煤层还是倾斜煤层开采，上覆基岩断裂均存在破断角度，岩层裂隙带发育范围近似可认为“梯形”大结构;FORSTER和ENEVER[8-9]以澳大利亚的大煤层超临界长壁面板为基础，建立了一个实用的水文地质模型，该模型描述了岩层垮落带与裂隙带也为一个“梯形”大结构，并且更近似于“倒漏斗式”拱形。郭文兵等[10]认为开采强度与覆岩运移程度有关，揭示了高强度开采条件下覆岩“两带”破坏模式与形成机制;许家林等[11-13]基于关键层理论，提出了一套更为合适和准确的岩层“三带”高度计算方法。

地表沉陷状态与影响范围是采取土地复垦、地下管线布置以及村庄农田保护的依据。目前预测地表沉降与岩层移动的普遍方法是经验法与数学方法相结合，其本质属于一种数学方法，即通过从几何、数学的方法，描述采矿现象[14-15]。早期我国煤炭主要开采区域煤层埋深浅、地质构造简单，许多矿区可以通过传统“倒漏斗式”沉降曲线进行地表沉降影响预测。随着开采深度增大，地质结构变得复杂，若覆岩中存在较厚的松散层，传统地表沉降预计方法的精确性将由此受到影响[16-18]。厚松散层开采条件下岩层运动不仅是岩层破断后的块体运动，也是位于岩层至地表之间松散层的散体的组合运动。基于此，笔者[19]率先将地表沉陷与基岩破断建立起联系，揭示了岩层移动与地表沉降的力学本质。以关键层理论为基础，通过具有明确物理意义的岩层移动“类双曲线”模型将地表沉降与岩层移动边界统一为整体。为了使岩层移动边界“类双曲线模型”适应更多复杂地质条件，而后还发展了更为精细化的“类双曲线”识别模型[20-23]。此外，以岩层移动边界“类双曲线”模型为基础，在再生顶板岩体巷道围岩支护体系中也进行了应用，建立了再生顶板“抛物线—半双曲线”扩展力学模型[24]。

伴随着 “绿色采矿”与“科学开采”精神内涵不断丰富，促使需要寻求一个更加关键合理的评价体系和力学模型解释岩层移动与地表沉降之间复杂的力学关系[25-26]。因此，笔者以岩层移动破断边界“类双曲线”模型为基础[19]，将厚松散层“漏斗式”沉降拱与岩层移动“倒漏斗式”冒落拱进行联系，通过内“类双曲线”模型描述。建立了厚松散层近水平煤层开采整体岩层移动与地表沉降内、外 “类双曲线”整体模型以及共轭条件。运用UDEC数值计算方法获得了厚松散层覆岩共轭内外“类双曲线”模型破断运移规律，一定程度上验证了理论分析，为更准确预计厚松散层覆岩移动提供指导。

1 覆岩“拱式”冒落与裂隙带破断机理

1.1 基岩破断“倒口拱形”块体结构假设

煤层开采岩层达到极限跨距时会发生初次破断和周期破坏，岩层破断规律具有周期性。当回采工作面沿倾斜方向的长度远大于沿走向方向的跨距时，岩层的破断可以认为是拉剪破坏的耦合[27-28]。其中，岩梁初次断裂固支梁结构任意一点的应力分量的表达式[19]为

(1)

式中，q为上覆岩层的载荷;h为岩梁的高度;l为岩梁的跨度。

岩梁周期破断悬臂梁结构任意一点的应力分量的表达式为

(2)

如图1所示，通过Matlab软件编程可直观体现基岩初次断裂与周期断裂最大剪应力云图。假定q=3 MPa，岩层厚度h=20 m，高跨比为1。可以观察到，岩梁初次破断时两边固定端附近受剪切应力作用，形成斜拉破断，破断岩梁近似为梯形结构。类似地，周期破断岩体在固定端上边缘为剪应力集中区，破断后形成倾斜式贯穿裂缝，破断结构形态同样也为梯形结构。

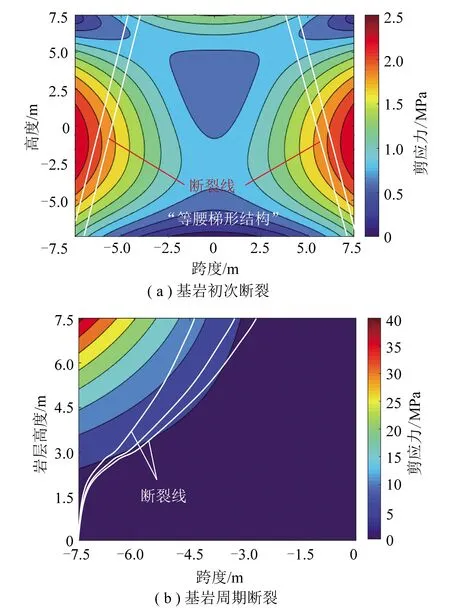
图1 基岩断裂主应力迹线分布Fig.1 Distribution of main stress trace of bedrock fracture

文献[19，29]认为基岩的破断移动区呈台阶式倒漏斗形，原因包括2方面:① 基岩各岩层间为非线性、非连续破断，出现倒漏斗形台阶;② 各岩层断裂迹线呈倒漏斗形梯形块体结构。在宏观尺度上若忽略岩层破断迹线，可将整体组合岩梁断裂轨迹的梯形结构近似为开口向下的“倒口拱形”。如图2所示，一般来说，主关键层以下岩层的破断和移动范围由深至浅将逐渐减小，即各岩层组合从下至上破断的梯形破断块体分布密度由浅至深将不断减小。因此，若将主关键层以下组合岩层视为统一岩体(组合岩梁h远大于2l)，则关键层以下的整体岩层大结构破断形态也为梯形结构。“拱形”假设将岩层宏观破坏与不规则裂隙分布规律统一，简化了复杂的非线性问题。两拱的大小与状态的变化规律对煤层群上行开采、强含水层或承压水下采煤、下保护层开采等的安全开采距离评价具有重要指导意义。

1.2 冒落拱与裂隙带临界力学关系

采空区上覆岩层的拱形冒落破坏，其实质为冒落与稳定裂隙区岩体间的极限剪切破坏。图3为不同配比相似岩梁材料实际断裂形态与过程，岩层两端的破断线与水平线具有夹角，破断形态呈梯形的块体结构[29]，试验结果很好地验证了理论分析。

假定岩层垮落带与裂隙带为2个大型的统一冒落块体[27,30]。基于块体理论，对于整体顶板剪切冒落，以整体组合大结构冒落块体为研究对象，将大结构冒落块体视为梯形块体分析，如图4所示。

图2 基岩倒漏斗“拱形”断裂梯形结构Fig.2 Isosceles trapezoid structure of bedrock inverted funnel “arched” fault

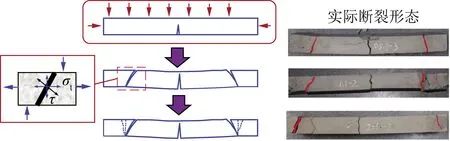
图3 不同配比相似岩梁材料实际断裂形态与过程[29]Fig.3 Actual fracture morphology of similar rock beam materials with different proportions[29]

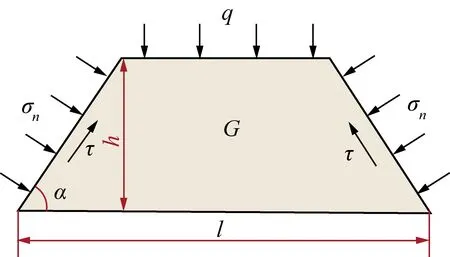
图4 梯形块体大结构力学模型Fig.4 Mechanical model of large structure of isosceles trapezoid block

考虑岩层块体的自重，根据对称性取块体的一半简化分析。根据图4可以得出梯形块体结构剪切面上的剪应力平衡满足式(3):

(3)

式中，α为剪切面与水平方向的夹角;G为块体结构的重力；σN为水平方向应力，其值等于顶板轴向应力与厚度的比值;f为剪切面滑动的摩擦因数。

其中，剪切面上的法向应力σn为

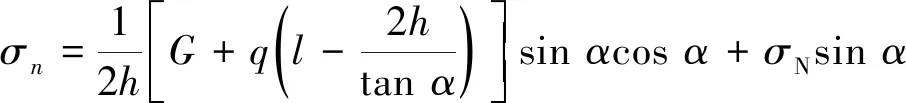
(4)

梯形块体自重应力为

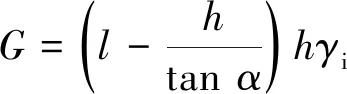
(5)

式中，γi为顶板岩层的容重。

假定岩层剪切破断满足摩尔-库伦强度准则:

τf=C+σntanφ

(6)

式中，τf为剪切面抗剪强度;C,φ分别为岩层黏聚力和内摩擦角。

定义r为剪切破坏安全系数，以反映整体组合顶板发生剪切破坏的可能性,其值等于剪切面抗剪强度τf与剪应力τR的比值:

(7)

其中，组合岩体大结构梯形冒落拱的剪应力为τR2;梯形小结构的剪应力为τR1。当r<1时(τf<τR2)，顶板沿剪切面滑移冒落。当r=rmin时，组合顶板大结构整体冒落高度的极限值为hc(hc可由顶板剪切破坏安全系数r求得)。当整体冒落拱大结构高度h>hc时，顶板剪切冒落破坏，冒落形状为拱形。若其中某一岩层剪应力τR2满足τf<τR2时，则垮落带以上的这一层岩体不发生拱式冒落，并且该岩层符合主关键层或亚关键层判定方法。

裂隙岩体破坏剪切力小于岩梁极限剪应力，岩层不发生拱式冒落，具有一定自承载能力，主要表现为整体下沉。如图5所示，一方面，岩体仅有未贯通裂隙，岩层自承载能力没有发生明显变化;另一方面，垮落带以上岩层虽然也形成了梯形块体式断裂，但是岩块间存在咬合关系。在工作面中部，可能形成外表似梁，实质是拱的裂隙体梁的“砌体梁”结构平衡关系[31]。一旦“砌体梁”结构发生滑动极限失稳时，即为“梯形”倒漏斗式拱形结构滑落。这从力学的角度解释了裂隙带大结构岩层的“倒漏斗”拱式特征。

图5 “倒漏斗式”拱形冒落岩块咬合点处极限平衡结构Fig.5 Limit equilibrium structure at the joint point of “inverted funnel” arch caving block

1.3 厚松散层“漏斗拱形”运移机理

厚松散层力学特性与移动变形规律与覆岩差异较大。工作面推进冒落拱与岩层裂隙拱扩展和移动使地表沉降、移动曲线不断变化。典型的厚松散层随开采地表沉降动态下沉曲线如图6所示。随着工作面的推进，地表下沉盆地逐渐扩大，下沉值增大。整个开采过程中地表沉降和移动曲线整体表现为“漏斗式拱形”。随着工作面不断推进，漏斗式拱形深度达到最大值(3 931 mm)不再继续增大，而是地表下沉盆地水平影响范围不断增大。

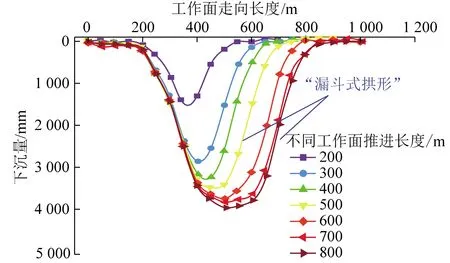
图6 厚松散层随开采地表沉降动态下沉曲线 (山东兖州矿区鲍店煤矿)[32-33]Fig.6 Dynamic subsidence curve of thick loose layer with mining surface settlement(Baodian coal mine in Yanzhou mining area,Shandong Province)[32-33]

覆岩冒落拱为其他相对稳定的岩层滑落与旋转提供了空间，其形态和大小影响地表沉降范围。目前普遍采用概率积分法进行预测地表沉降，随机介质理论中将厚松散层视为非连续的颗粒介质。假设厚松散层中散体半径ri越靠近地表越小，沉陷区域呈漏斗式拱形，如图7所示。地表的下沉量W(x，z)与水平移动量U(x，z)表达式[34-35]为

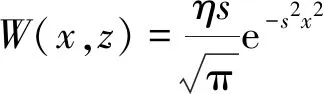
(8)

(9)

式中，η为开采系数(η≤1)，取决于顶板管理方法;s为积分系数，只与纵坐标z和时间t有关;B(z)为水平移动系数。

图7 厚松散层剪切滑移及移动机理Fig.7 Shear slip mechanism and movement model of thick loose layer

由于概率积分法以移动观测资料和数学方法为基础，在描述厚松散层水平煤层开采地表移动时存在预测模型参数物理意义不明确、预测参数不易确定、岩层力学本质揭示不清等问题[15]。因此，若忽略地下水砂流动、厚松散层失水压缩和塑性变形等因素，从力学角度将厚松散层的移动过程分为3个阶段:滑移—拉裂—剪断[19]，如图7所示。松散层的抗剪强度较低，在松散层下部易沿着与水平面成45°+φ/2角发生剪切滑移破坏。由于厚松散层压实程度越靠近地表越小，内摩擦角φ也越靠近地表越小，地表拉裂角也将减小。这里从力学的角度解释了松散层沉降曲线并不是一条直线，而是类似“漏斗式拱形”沉降曲线。

2 内外“类双曲线”模型

2.1 岩层移动边界外“类双曲线”模型

为了从几何、数学的方法，描述采矿现象并赋予数学方程明确的物理意义。笔者将厚松散层开采地表沉降和岩层移动两者建立联系[19-23]，并希望岩层破断和地表沉陷研究有机地形成整体。不同于严格数学意义上的“双曲线”，在实际采矿工程中“双曲线模型”具有一定的相似性。因此，在建立模型描述和应用时，通过“类”字对“双曲线模型”进行描述。以采场上覆岩层关键层理论为基础，建立了充分采动厚松散层岩层破断移动边界的类“双曲线模型”。岩层移动破断边界“类双曲线模型”为近似“左右”对称关系。为了便于区分，将岩层移动破断边界“类双曲线模型”以岩层移动破断边界外“类双曲线模型”命名，如式(10)所示:

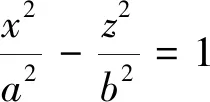
(10)

将点(D/2，H)代入式(10)中，可得地表沉降范围D的计算式(11)。该公式将基岩的倒漏斗型破断和厚松散层的漏斗型移动统一，更利于准确预计地表沉陷。

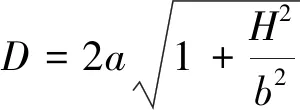
(11)

2.2 岩层移动与地表沉降内“类双曲线”模型

厚松散层地表沉降曲线近似“上凹”漏斗式碗状拱，采空区垮落带近似“下凸”倒漏斗式冒落拱。2者在数学上有近似“上下”对称关系，关键层或关键层周边某一岩层即为 “两拱”的对称岩层(对称轴)。本节仅考虑整体冒落岩层剪切力大于其剪切强度形成梯形块体冒落情况。假设主关键层位置位于7～10倍采高以外，裂隙带发育高度由最近的亚关键层控制[11-12]，即认为垮落带和裂隙带的发育高度不超过主关键层高度。

若不考虑岩性变化、断层构造、陷落柱以及开采方式等因素，在厚松散层水平煤层开采条件下，以关键层为基础建立坐标系。可将图8中地表移动、沉降曲线、覆岩裂隙拱和冒落拱边界曲线通过焦点在z轴上的 “类双曲线”模型整体描述。双曲线模型开口大小受开口率(离心率)控制。因此，根据建立岩层移动与地表沉降“类双曲线”模型能体现出阶段差异，能够较好地描述地表沉降与岩层移动的整体关系。

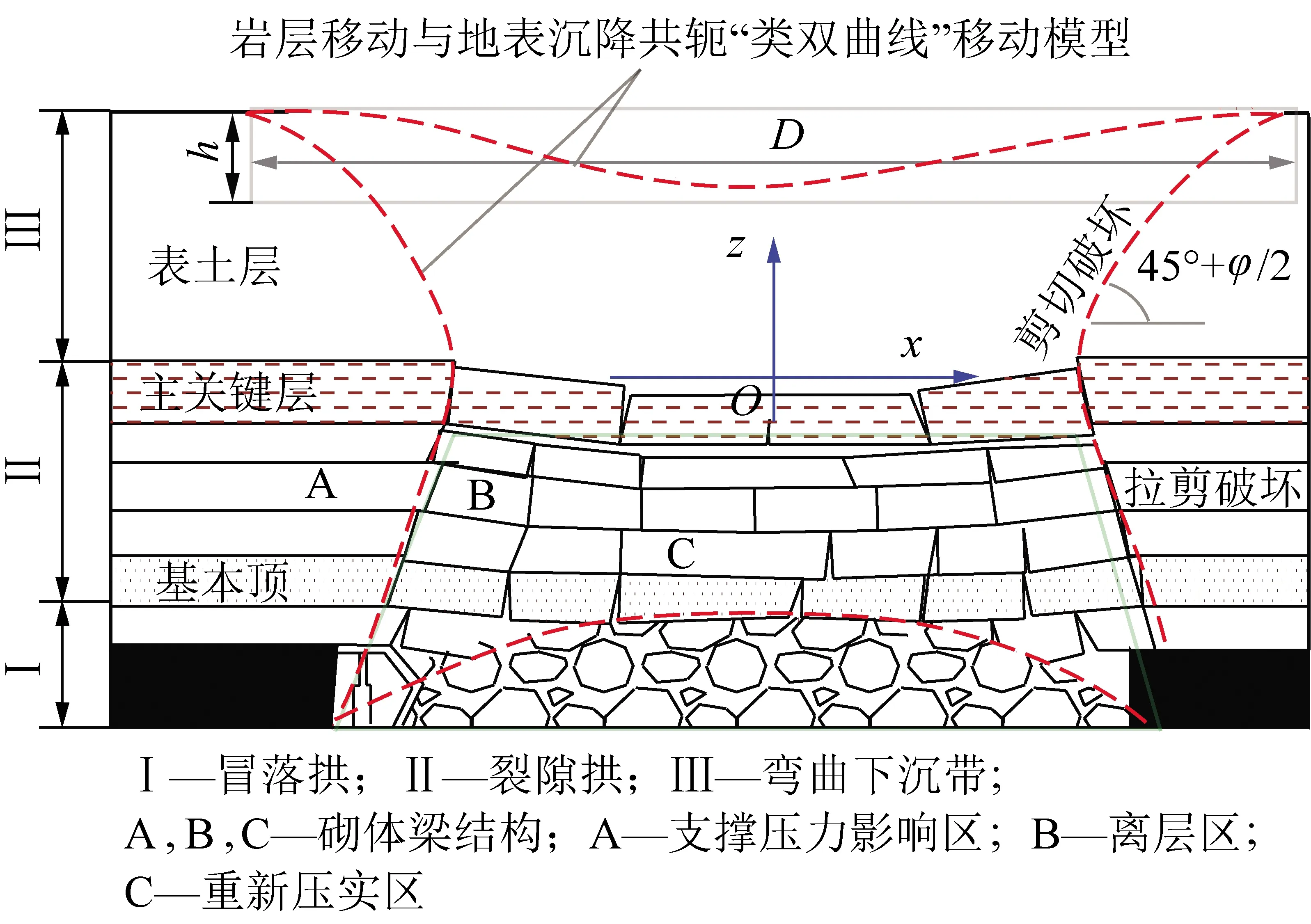
图8 岩层移动移动与地表沉降共轭内外“类双曲线” 整体移动模型Fig.8 Conjugate analogous hyperbola model of strata movement and surface subsidence

厚松散层水平煤层开采岩层移动与地表沉降内“类双曲线”整体模型表达式为

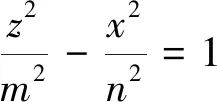
(12)

其中，m，n为双曲线的实轴和虚轴长。

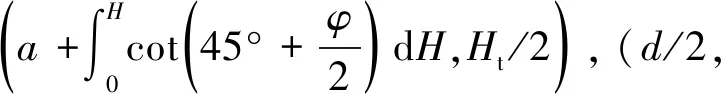
(13)

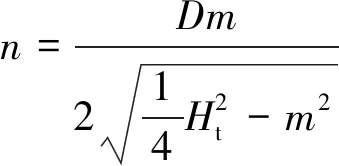
(14)

若获得实测松散层厚度，将点(0，Ht-H1)代入双曲线模型，即可预计地表沉降移动最大值H1=Ht/2-m。地表沉降与岩层移动在纵方向的变化轮廓通过岩层移动与地表沉降内“类双曲线”模型描述。

式(10)与(12)统称为厚松散层水平煤层开采岩层移动与地表沉降的内外“类双曲线”整体模型。准确来说，外“类双曲线”模型指的是岩层移动破断边界“类双曲线”模型，在工作面的中垂线附近似“左右”对称关系;内“类双曲线”模型指的是至充分采动覆岩倒漏斗拱式垮落带、拱式裂隙带与地表漏斗式沉降移动拱曲线，关于关键层附近岩层近似“上下”对称。

2.3 内外“类双曲线”模型共轭条件

以岩层移动边界外“类双曲线”模型为基础，将物理参数的a与b进行联系，建立整体内外“类双曲线”模型。两者受工作面推进距离d、采高、覆岩和松散层高度等影响。若岩层移动与地表沉降内外“类双曲线”模型中物理参数a≈n，b≈m时，即内、外 “类双曲线”有近似共同渐近线，“类双曲线”模型关于坐标轴近似上下、左右对称。此时，两组“类双曲线”模型即有数学上的近似共轭关系，称共轭内外“类双曲线”整体移动模型。此外，岩层移动破断边界外“类双曲线”模型以关键层为基础建立，共轭“类双曲线”模型与主关键层近似对称。

需要指出的是，在实际工程中受岩层构造、地下水等复杂地质条件影响，共轭内外“类双曲线”模型为岩层移动内外“类双曲线”模型的一个特例。地表最大下沉值点与地表下沉边界连线与水平面的夹角为松散层沉降角ξ(一般小于45°+φ/2)。地表沉降范围D越大，地表沉降角越小。若岩层移动与地表沉降内外“类双曲线”模型有近似共轭关系时，则描述岩层移动地表沉降共轭内外“类双曲线”模型的地表移动和地表沉降角ξ有如下近似关系:

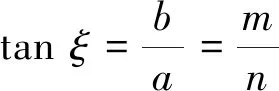
(15)

3 内外“类双曲线”模型实测验证

笔者选取国内典型厚松散层近水平煤层工作面的走向或倾向实测地表沉降数据[33,36-37]，对岩层移动与地表沉降内外“类双曲线”整体模型进行对比验证。由于部分矿区松散层和基岩的力学参数资料存在缺失，故将基岩冒落角和厚松散层内摩擦角近似认为恒定值。其中基岩冒落角约为70°、松散层内摩擦角约为22°。列举和验证国内厚松散层矿区地表实测移动和理论验证见表1。“类双曲线”理论模型对水平厚煤层(采高>3 m时)沉降预测值较准确，实测岩层移动范围与地表沉降最大值与理论模型预测值误差控制在10%以内。理论模型与实际值的误差较小，可见在厚松散层水平煤层开采条件下，岩层整体移动存在“类双曲线”特征，岩层整体移动内外“类双曲线”模型与实际结果基本吻合。

表1 统一岩层移动“类双曲线”模型实测与验证Table 1 Measurement and verification of analogous hyperbola model

需要指出的是，充分采动煤层地表下沉与岩层沉降达到极限值。在此后，地表沉降盆地垂直沉降减小，水平影响范围增大。通过内外“类双曲线”整体模型离心率(开口率)可描述动态地表沉降与开采岩层移动。

4 岩层移动与地表沉降离散元模拟

4.1 模型建立

离散元程序UDEC在非连续介质(如节理岩体)静载荷或动载荷作用下的响应具有一定优越性，适合模拟块状系统(如研究开采岩层移动规律等)的大运动和大变形。如图9所示，通过使用UDEC中Voronoi细分生成器(Voronoi Tessellation Generator)，岩石块体可以表示为在其接触面上结合在一起的随机溶聚的刚性体或可变形多边形子块的堆积。UDEC-DM随机大小的胶结多边形与结晶岩和沉积岩的颗粒界面或颗粒胶结特性相连，从而与自然发生的破坏过程非常相似，因此这在模拟地下采矿地表松散层中有较大的优势[38-39]。

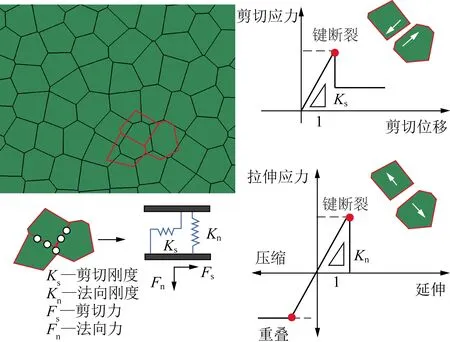
图9 UDEC-Voronoi组件的微观特性和本构接触行为[38-39]Fig.9 UDEC Voronoi assembly micro-properties and constitutive contact behaviour[38-39]

本节以山西省安太堡煤矿地质条件为基础，通过UDEC 7.0建立数值计算模型。如图10所示，模型尺寸为500 m × 157 m，根据安太堡煤矿的覆岩地质条件自下而上一共划分了12组岩层[22,40]。其中，9号与5号砂岩分别为亚关键层与主关键层。松散层通过UDEC-Voronoi生成并赋予模型参数(表2)。数值模型两边和底部边界条件通过位移固定，侧压系数为1.1。

安太堡煤矿目前主要采用综合机械化放顶煤方法开采4号煤层，4号煤层厚度6.5 m，平均埋藏深度约为100 m。放顶煤厚度3.5 m，长壁开采宽度200 m。4号煤层及其上覆岩层地质条件简单，无断层和水文影响，地层近似水平分布。煤层上覆直接顶为页岩，基本顶为砂岩。上覆岩层顶部有较厚的松散层。

4.2 计算结果与讨论

图11为不同推进距离岩层移动与地表沉降规律情况。岩层移动与地表沉降内外“类双曲线”整体模型随着开采推进具有阶段化发展，具体为:① 煤层推进至40 m时，亚关键层未发生破断仅有小范围下沉，此时直接顶仅发生小范围离层，地表几乎不沉降。② 煤层推进至80 m时，直接顶初次冒落，直接顶倒漏斗式梯形拱形成，主关键层未发生破断。基本顶与关键岩层仅发生小范围下沉，地表沉降范围影响较小;③ 煤层推进至160 m，关键层破断，岩层裂隙带发育至主关键层，采空区冒落拱范围变大。采空区上覆岩层整体下沉直接影响至地表发生“漏斗式”下沉拱。岩层整体移动与地表沉降内外“类双曲线”轮廓初步形成;④ 当煤层推进至240 m时，采空区冒落拱被整体岩层下沉接顶，采空区进一步压实，地表下沉拱范围不断增大，最大下沉量趋于稳定;岩层整体移动与地表沉降内外“类双曲线”轮廓相应扩展。 如图11(e)所示，“类双曲线”理论预测值与模拟最大下沉结果误差较小，能够较好地反映岩层移动与地表沉降整体变形规律。需要指出的是，地表沉降内“类双曲线”模型在地表沉降移动边界的描述有一定限制。需要结合岩层移动破断边界外“类双曲线”模型共同描述。

图10 安太堡煤矿UDEC数值模型Fig.10 UDEC numerical model of Antaibao coal mine

表2 块体之间接触力学参数[22,40]Table 2 Contact mechanical parameters between blocks[22,40]

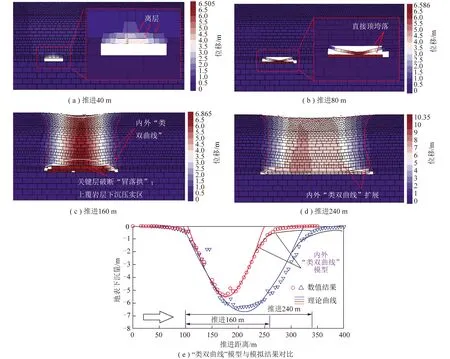
图11 岩层移动与地表沉降内外“类双曲线”形成位移云图Fig.11 Formation of analogous hyperbola model inside and outside of strata movement and surface subsidence

5 结 论

(1)以岩层移动破断边界外“类双曲线”模型为基础，建立了岩层移动与地表沉降内外“类双曲线”整体模型。与传统“漏斗式”岩层移动边界曲线不同，该模型能更加精确地描述上覆岩层与地表沉降的整体移动规律，弥补传统岩层移动曲线预测精度的不足。其中外“类双曲线”模型指的是岩层移动破断边界“类双曲线”模型，在工作面的中垂线近似“左右”对称;内“类双曲线”模型指的是覆岩冒落、裂隙拱与地表漏斗式沉降移动拱“类双曲线”模型，在关键层近似“上下”对称，其与岩层的物理力学性质有关。

(2)分析了共轭内外“类双曲线”模型形成的共轭条件、影响因素与整体运移规律。岩层移动与地表沉降内外“类双曲线”岩层移动模型的形成过程具有不同的阶段特性，受推进距离、推进速度、采高、松散层与基岩厚度比等影响，其中采高与推进距离对模型预测精度影响较大。

(3)通过国内典型厚松散层近水平煤层开采工作面的走向或倾向现场监测数据，以及理论分析和数值模拟结果表明，建立的岩层移动与地表沉降内外“类双曲线”整体模型理论预测值与实际值误差较小，表明岩层整体移动存在“类双曲线”特征。