基于BP 神经网络的手写字符识别

陆文玲

(南京林业大学,江苏南京 210037)

0 引言

人工神经网络的发展历史相当悠久,早在1958年,研究认知的心理学家Frank便发明了感知机,这在当时掀起一股热潮。后来Marvin Minsky和Seymour PA pert发现感知机的缺陷:不能处理异或运算,计算能力也不足以处理大型神经网络。1979年,Fukushima提出神经认知机,诞生了卷积与池化的初步理论。H in t on 组的A le x N et 在ImageNet上以巨大的优势夺冠,引起深度学习的热潮,人工神经网络再次登上舞台。

由于金融、信息等行业的发展极大增加了生活生产中的数据交互,传统人工处理方式在大规模的数据统计中有着非常明显的劣势:耗费大量的时间与人力,自动化的处理方式需求应运而生。阿拉伯数字作为国际通用数字,形状信息量小,种类少的字符,不但具有很高的应用价值,同时拥有很高的理论价值,也因此率先被应用到手写体识别的研究中。文章基于PyCharm开发环境,使用Google于2016年开源的深度学习框架TensorFlow,搭建了全连接BP神经网络与卷积神经网络,利用来自美国国家标准与技术研究所(National Institute of Standards and Technology )发布的手写数字数据集MNIST与EMNIST进行测试与训练,通过监测训练过程中的各项参数,对隐含层层数,隐含层神经元个数,激活函数,学习率,优化器等参数不断优化,两种神经网络相互对比,最终完成的模型在MNIST下均能达到极高的识别水平,在EMNIST中也取得一定成果。

1 手写数字集MNIST

M N I S T 数据集来自美国国家标准与技术研究所,National Institute of Standards and Technology (NIST)。训练数据由来自250个不同人手写的数字构成,每个图像为784像素大小的正方形,其中50%是高中学生,50%来自人口普查局(the Census Bureau)的工作人员。测试集(test set)也是同样比例的手写数字数据。其中包含四个部分:

(1)Training set images:train-images-idx3-ubyte.gz(包含60000个样本)

(2)Training set labels:train-labels-idx1-ubyte.gz(包含60000个标签)

(3)Test set images: t10k-images-idx3-ubyte.gz(包含10000个样本)

(4)Test set labels: t10k-labels-idx1-ubyte.gz(包含10000个标签)

第一个32-bit是magic number,用于验证文件,第二个32-bit是样本数量。第三个32-bit表示图片行数,第四个32-bit表示图片列数,往后每个unsigned byte表示图像像素值。图像像素按行序展开,像素值为0到255,0表示白色,255表示黑色。整个数据以非常简单的用于存储矢量和多维矩阵文件的格式存储。文件中的所有整数均以大多数非英特尔处理器使用的MSB优先(高端)格式存储。

2 手写字符识别

2.1 BP神经网络

Back Propagation(简称BP)算法是人工多层神经网络中对权值更新起到重要作用的方法,它的本质简单理解就是复合函数的链式求导[1]。神经网络本质是作为数理统计的一种模型,拟合是该应用中一个常见场景,即需要利用已知的数据,做出适当的映射来描述这些样本与自变量的相关性[2]。对神经网络的训练同样为了这样一个目标,但这种情况下,样本不仅仅是二维坐标一一对应的x,y,而变成了由矩阵向量等组成的多维数据。同样的,样本数据也非常晦涩,难以用一个简单的映射来描述。但研究人员发现多层神经网络非常适合描述这种对应关系,而神经网络本质就是复杂的复合函数。

2.1.1 模型结构

文章搭建了两种不同隐含层数量的全连接BP神经网络模型,基于2.3中的原则,在两隐含层的模型中采用了2000与100神经元数,在三隐含层版本中采用6000-1800-200神经元数,输入根据MNIST的图像大小为784(28×28),输出种类一共为十种。

2.1.2 具体实现

建立模型需要首先确定Graph结构,完成定义输入层变量后,构建隐层1,定义了两个Variable,weights表示连接权重,其形状为[784,2000],biases表示偏置量,形状为[2000]。在隐层2中,weights形状为[2000,100],biases形状为[100]。输出层weights形状为[100,10],biases形状为[10],所有权重均初始化为0。基于上面的权重和偏置量值,初始使用sigmoid激活函数连接各层。在确定好模型各层结构和参数后,需要定义一个损失函数来设置对于误差的计算方式,实验的初始设置为最小二乘法。最后调用training方法,传入定义好的损失函数与学习率,为保险起见,初始学习率设置为0.2。TensorFlow提供的feed方法可以在运行时向Graph输入数据。在每一步训练过程中,数据并不是逐个供给,而是根据定义的batch大小按批次供给:

batch_size=100

n_batch=mnist.train.num_examples//batch_size

对于这两种模型,根据MNIST上的测试,决定采用性能最优的batch大小100,优化器选择为批量梯度下降法(Batch Gradient Descent,简称BGD),整个模型共迭代50次。

在三隐含层的模型中, 隐含层神经元分别设置为600,1800与200,其他设置采用与二隐含层模型相同的初始参数。

2.1.3 性能分析

监视了两种模型在迭代5 0 次中的正确率变化,为了观测模型的拟合情况,在使用训练数据训练模型后,同时分别采用训练数据与测试数据行进测试。对比两种模型分别在训练集和测试集上的效果,发现训练数据的测试效果与模型没有见过的测试数据效果差异相当微小,一般没有超出2 %, 因此可以认定, 全连接的神经网络在MNIST数据集上能很好的完成手写字符的识别任务,且拟合情况相当优异。通过对比,文章认为三隐含层模型更具有潜力。

2.2 卷积神经网络

当面对图像处理的实际应用,传统的全连接B P 神经网络的缺点显而易见,需要将整幅图像作为输入数据,由模型读取,随着图像的大小增加,对应的输入节点也因此增加,同样的,隐含层节点也必不可少的增加,因此全局的参数数量变得十分庞大,导致消耗大量的计算资源。人们仿照人眼对于图像的感知,发现识别图像其实是由局部衍生到全体的过程,小范围内的图像像素相关度高,全局中不同位置像素相关度低。所以,神经单元并没有必要对全局图像进行感知,只需要将局部作为输入,在模型的后期将各个局部信息拟合在一起,这种方法就是卷积神经网络的核心思想:局部感受野[3]。

2.2.1 模型结构

在卷积模型中,采用两次卷积-池化交替,再链接到一层全连接层进行输出[4]。输入同样是28×28大小,第一次卷积中,卷积核采用5×5大小,输出32张特征图,池化窗口采用2×2大小,步长为2,方式为最大池化。第二次卷积窗口仍为5×5,输出64张特征图,同样采用步长为,大小2×2的最大池化方式。随后链接到各个单元的全连接层。

文章依然在卷积模型的每一层加入了激活函数ReLU, 损失函数的选择为交叉熵函数,其中优化器选择了Adam Optimizer,学习率设置为0.01。考虑到卷积模型的训练时间较长,并且在实际应用中的性能比较优异,将迭代次数设置为15次。

2.2.2 性能分析

使用TensorFlow内置的可视化工具tensor board跟踪神经网络的整个训练过程中的信息,包括每一层权值与偏置的最大,最小与均值。来监测模型的训练过程是否出现停滞或者参数爆炸等意外情况。在多次对卷积模型的训练后发现,模型中的参数均以比较健康的方式变化,损失函数的收敛也处于一个比较稳定的状况,根据A d a m Optimizer的特性,将学习率降低了一个数量级,设置为0.001。在卷积网络中,将这些神经单元随机分配了约等于零的权值。权重可以表示为0.001×N(0,1),其中N(0,1)是均值为0,标准差为1的高斯分布。同样利用均匀分布赋予权重初始值也是一个不错的选择,虽然权重最终都会收敛到近似的数值,但在训练初期更加利于模型进入收敛状态,而且避免了因为神经元饱和引起的学习减速。

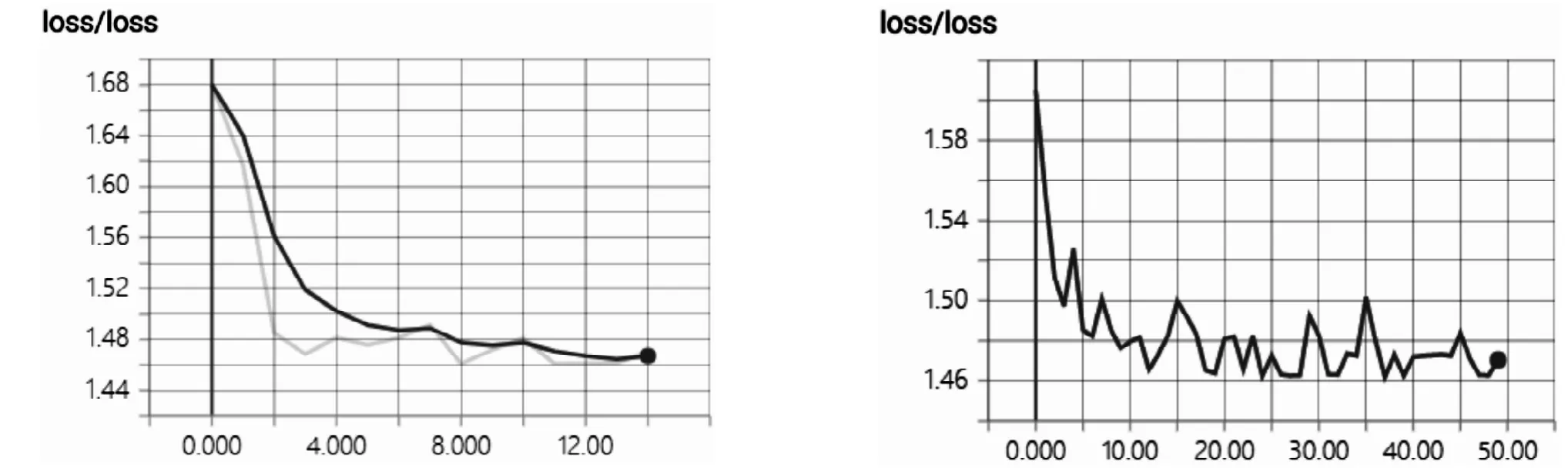
图1 卷积模型的损失函数与全链接模型的损失函数变化Fig.1 Variation of loss function of convolution model and full link model

2.3 两种神经网络的性能比较

得益于Adam Optimizer的优势,卷积模型的损失函数收敛速度十分快,并且相当稳定,而全连接模型中损失函数在初期虽然下降速度也相当快,但在随后的训练中剧烈震荡,即使总体处于一个较低水平,这也导致了测试正确率的震荡。如图1所示。

就正确率而言,两种模型都达到了超过99%的水平,虽然全连接模型的迭代次数50远高于卷积模型的15次,但总体训练时间相当。按训练时间比较,两个模型都在前期迅速收敛,后续训练中,全连接版本的正确率略有震荡,但大体不超过1%水平,卷积版本则更加平滑。

3 结论

以上两种模型的使用还处在一个比较初级的阶段,一是对比较简单的手写数字进行分类,二是数据集选取了这一领域的经典数据集M NI S T,对于模型的泛化能力还有待测试。使用深度卷积网络对EMNIST的测试也只是取得了一个比较平庸的水平。目前,世界范围对手写字符的识别已经处于一个比较成熟的水平,对样本质量的要求逐渐降低,识别率逐渐增加,有关研究也深入到不同语言,不同个体的差异。虽然这里同样取得了极高的正确率,但在时间与计算资源的消耗上仍有进步空间,字母数字的混合甚至汉字数据集上的改进测试也是可以涉及的领域。