波动方程初至双差走时层析反演
2021-03-23王华忠
赵 磊,冯 波,王华忠
(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.同济大学海洋与地球科学学院波现象与智能反演成像研究组,上海200092;3.同济大学海洋高等研究院,上海200092)
地震波走时多用于中、大尺度的速度结构特征反演。对于有限频带的地震信号,地震波走时(绝对走时)受震源子波的初相位、走时测量准则(如起跳时刻、包络极值时刻,最大峰值时刻)等多种因素的影响。地震波走时的测量误差会降低反演结果的精度及可靠性。为尽可能降低绝对走时测量误差对反演的影响,BRUNE等[1]提出采用“相对测量值”代替“绝对测量值”以减少测量误差。基于此方法测量的地震走时亦称为双差走时(double-difference traveltime),可以用于提高震源定位精度[2-4],反演高精度速度模型[5]。
传统的双差走时层析反演方法多基于射线理论,存在焦散及阴影区等问题[6],且反演精度不高。对于小尺度异常体(速度非均匀体的尺度小于菲涅尔体的宽度),有限频理论[7-14]可以更好地处理地震波的一阶绕射效应[15-16]。YUAN等[17]将双差走时测量方法引入伴随层析(adjoint tomography),得到了更高精度的反演结果,但双差走时敏感度核函数仍采用Born近似计算方法计算得到[11]。相较于Born近似,Rytov近似可以更好地描述由于速度扰动引起的前向散射波相位扰动[18],因而更适用于走时反演。本文利用Rytov近似构造走时敏感度核函数[19-26],即将双差走时测量方法与Rytov走时敏感度核函数相结合,提出了一种新的波动方程初至层析反演方法。该方法在保留Rytov近似优点的同时,可以降低甚至消除走时测量误差对反演结果的影响。
1 理论
1.1 双差相位延迟敏感度核函数
频率域标量声波方程可以表示为:
(1)
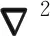
令扰动后的速度场为v(x),总场为u(x;ω),总场与背景场的关系表示为:

(2)
式中:ψ(x;ω)为复相位。
利用Rytov近似,将单频谐波的相位延迟表示为:
=〈Kp(x,ω;xr,xs),Δm(x)〉M
(3)
式中:Im表示取复数的虚部;Δm(x)为慢度平方扰动(属于模型空间M),Δm(x)=v(x)-2-v0(x)-2;xs,xr分别代表震源和检波器横坐标;Kp(x,ω;xr,xs)为相位延迟敏感度核函数[25]。Kp(x,ω;xr,xs)可表示为:
Kp(x,ω;xr,xs)=
(4)
(3)式所预测的相位延迟假定了u和u0由相同的震源产生。若震源子波未知,复相位中包含子波剩余相位差。在全波形反演中,通常用褶积[27]或反褶积[28-31]类方法消除震源子波对反演的影响。本文采用反褶积方法,引入如下反褶积波场:
(5)
式中:xi和xj为同一炮集中任意不重合的两个检波器横坐标;uw(xi,ω;xs)和uw(xj,ω;xs)分别为初至波形加窗前、后的地震信号(频率域)。uw(xi,ω;xs)可表示为:
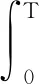
(6)
式中:h(t)为初至波形窗函数,用于提取初至震相;*为卷积运算符号;h(ω)为窗函数的频率响应。
令uw(xi,ω;xs)=f(ω)A(xi,ω;xs)eiφ(xi,ω;xs),uw(xj,ω;xs)=f(ω)A(xj,ω;xs)eiφ(xj,ω;xs),其中,f(ω)为震源子波频谱,A(ω),φ(ω)分别为格林函数的振幅谱和相位谱,初至波形的相位差Δφi,j(ω;xs)可以表示为:
Δφi,j(ω;xs)=φ(xi,ω;xs)-φ(xj,ω;xs)≡Im[lnvi,j(ω;xs)]
(7)
显然,子波频率对地震信号相位的影响被抵消了。采用双差测量方法[5],得到的观测数据和模拟数据的双差相位延迟可以表示为:
(8)

综合考虑(2)式至(7)式,初至波形的相位延迟和模型扰动的线性关系可表示为:

(9)
将(9)式代入(8)式,双差相位延迟与模型扰动的线性关系可表示为:
(10)
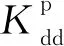
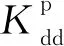
(11)
1.2 双差走时敏感度核函数
有限频带地震信号的走时扰动可以表示为单频谐波的相位延迟的加权叠加[22],即:
(12)

同理,双差走时扰动与双差相位延迟的关系可表示为:
(13)
将(10)式、(11)式与(13)式相结合,可以建立双差走时扰动与模型扰动的线性关系:
(14)
式中:Kdd(x;xi,xj,xs)为(带限信号或有限频)双差走时敏感度核函数。Kdd(x;xi,xj,xs)的表达式如下:

(15)
式中:K(x;xr,xs)为基于Rytov近似的有限频走时敏感度核函数[24-25]。
冯波等[25]给出了Rytov近似走时敏感度核函数K(x;xr,xs)在时间-空间域的显式计算公式为:
(16)

1.3 走时层析反问题求解
基于走时残差L2范数的误差泛函可以表示为:
(17)
假定每个震源有Nr道地震记录,随机采用第i个地震道作为参考道,其它地震道与参考道计算得到的双差走时为ΔΔti,j,满足1≤j≤Nr且j≠i。
采用Gauss-Newton反演算法,将模型参数更新过程表示为:
mk+1=mk-αkP[H-1(mk)g(mk)]
(18)

由(15)式可知,泛函梯度g(mk)可以用核函数与走时残差表示为:
(19)
(20)
(19)式可以表示为:
(21)
式中:λdd(x,T-t;xs)为双差走时伴随震源逆时传播产生的伴随波场。
为避免直接Hessian矩阵求逆,可以通过求解如下方程的近似解获得模型更新方向:
H(mk)Δmk=g(mk)
(22)
本文采用共轭梯度(conjugate gradient,CG)法求解方程,采用冯波等[25]提出的隐式矩阵向量乘法得到高效的Hessian向量积,无需显式计算及存储Hessian矩阵。具体计算公式见附录A。
2 数值试验
2.1 高斯扰动模型测试
我们设计了一个含有高斯异常体的速度模型v(x,z)=v0+δv(x,z),其中背景模型v0为匀速模型,高斯异常体δv描述如下:
(23)
式中:ε为速度扰动百分比;v0=2500m/s为均匀背景速度;a为高斯异常体的尺度参数;(x0,z0)为高斯异常体的中心坐标,(x0,z0)=(2500m,2500m)。
采用10m×10m的网格离散化含有高斯异常体的速度模型,x和z方向网格数目均为501。高斯异常体的尺度参数a=500m,速度扰动百分比ε=10%(图1a)。为消除采集孔径对反演结果的影响,本文设计了一个四周激发-接收的观测系统,在模型四周放置100个均匀分布的震源,每边25个震源。每炮由100个检波器接收,检波器均匀分布在模型四周,并与震源重合。正演采用10Hz主频的Ricker子波(对应波长λ0=250m,与异常体尺度参数满足a=2λ0)。
为了验证本文双差走时反演方法的有效性,我们首先对每个震源子波引入随机延迟,并采用有限差分方法模拟观测地震记录。本文采用SEISCOPE数值优化软件包(SEISCOPE optimization toolbox[31])中的截断牛顿算法(对于走时层析,截断牛顿算法退化为高斯牛顿算法)求解双差走时目标函数。根据附录A中的隐式矩阵向量积计算公式计算梯度与Hessian向量积。初始模型采用匀速背景(v0=2500m/s),震源子波采用0.5s延迟的Ricker子波(10Hz主频)。目标函数的终止准则为检测目标函数的相对误差(σ=J(mk)/J(m0))小于预先给定的门槛值σ=1.0×10-4。步长采用线性搜索估计,每个高斯牛顿方向采用2次CG内迭代求解(16)式。经过10次高斯牛顿方向迭代求解,得到的速度扰动(图1b)最大值为249.7m/s,与真实速度扰动的最大值250.0m/s基本一致。
接着我们根据相同的反演参数,利用绝对走时[25]层析反演方法进行反演,将正演观测数据得到的随机延迟Ricker子波作为震源,得到的速度扰动如图1c所示。可以看出,采用双差走时与绝对走时层析反演方法得到的速度扰动均与真实速度模型吻合较好。因此对于完备的观测系统,双差走时层析反演与常规反演结果基本一致,证明了双差走时层析反演方法的有效性。

图1 含有高斯异常体的速度模型(a)、采用双差走时(b)与绝对走时(c)层析反演方法得到的速度扰动
2.2 Overthrust模型测试
为进一步测试本文方法在近地表速度建模中的效果,我们用SEG/EAGE Overthrust速度模型[32]正演观测地震数据。原始速度模型在x和z方向网格数目分别为801和187,网格间距为25m。为更好地反演速度模型左侧的推覆构造,我们将速度模型左右侧分别拓展,得到一个横向长度为25000m的SEG/EAGE Overthrust近地表速度模型(图2a)。我们设计了一个陆上单边偏移距观测系统,在地表放置91个均匀分布的震源,炮间距为200m,每炮由117道检波器接收,道间距为25m(最小偏移距100m,最大偏移距3000m)。观测地震记录由有限差分算法计算得到,地震子波主频为8Hz且存在随机延迟的Ricker子波。
由于观测地震记录较为复杂,本文采用自动初至拾取算法得到观测数据和模拟数据的初至,并计算其双差走时(参考道为最小偏移距地震道)。初始模型采用线性递增的速度模型,当z=0时,v=2400m/s,当z=3000m时,v=4000m/s,震源子波采用8Hz主频的Ricker子波(子波延迟时间为0.2s),采用截断牛顿算法计算模型更新方向,每个方向1次CG内迭代求解(16)式,并用线性搜索方法估计迭代步长。在反演过程中,采用了多偏移距反演策略(从最长偏移距(3000m)逐渐减少到最小偏移距(500m)),最终采用双差走时层析反演方法得到的速度模型如图2b所示。可以看出,大尺度的近地表速度结构特征恢复得较好。图2c为利用该反演方法得到的速度扰动,主要表现为近地表中-大尺度的速度更新,最大有效反演深度约为150m。
图3为不同深度处速度横向抽线对比结果,显然双差走时层析反演结果在浅层的分辨率较高,甚至能分辨中、小尺度的速度异常。随着深度增加,其反演精度逐渐降低(有效反演深度由最大偏移距及速度结构共同决定)。

图2 横向长度为25000m的SEG/EAGE Overthrust近地表速度模型(a)、采用双差走时层析反演方法得到的速度模型(b)及速度扰动(c)

图3 不同深度处速度横向抽线对比结果
2.3 二维陆上实际地震资料测试
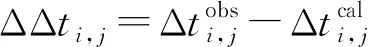
采用中国某地二维陆上实际地震资料(共1638炮,双边接收,最大偏移距7132m;炮间隔60m,道间距10m)进行测试,该地震资料采用初至自动拾取方法得到(拾取起震时刻)。初始模型采用线性递增速度模型(起伏地表之上用空气速度填充),震源子波为主频为10Hz的Ricker子波,基于相同的初至拾取标准得到模拟数据的初至,并采用多偏移距反演策略(最大偏移距分别为3000m,2000m,1000m,500m,每个尺度迭代8次),得到如图4所示的最终反演结果,可以看出最大有效反演深度约为700m。从反演结果可以看出,山间低速带得到了较好的刻画(近地表速度低至800m/s,低速带厚度约为200m),这与野外实际地表露头结果相符,速度模型左侧的平原地带,反演结果表现出明显的成层性。

图4 二维陆上实际地震资料反演结果
3 结论
为减小未知地震子波波形(或延迟时)及走时测量方法对(绝对)初至时间检测带来的误差,本文对观测数据和模拟数据采用相同的初至拾取方法并计算双差走时,以降低甚至消除走时测量误差对反演结果的影响。虽然根据公式推导,严格的双差走时应该采用加权相位延迟计算得到,但在实际应用中直接采用(自动或人工)拾取的初至计算双差走时得到的结果仍然是稳健的。
相较于传统波动方程走时反演方法中引入的一阶Born近似(要求速度异常体的尺度和扰动强度都足够小),本文结合双差走时测量及Rytov近似构建相位延迟敏感度核函数,可以更好地预测由于(大尺度)速度扰动引起的前向散射波的相位扰动,因此降低了对初始模型精度的要求。
在反问题数值求解方面,本文由于引入了基于隐式矩阵向量积的高斯-牛顿迭代算法,故仅需波动方程Born模拟及逆时偏移算法即可高效计算高斯-牛顿搜索方向,无需显式计算和存储Hessian矩阵,因此适用于求解大规模计算问题。
附录A 隐式矩阵向量乘法
1) 矩阵向量积Kddp(p为模型空间中的向量p=p(x))。
根据(15)式,Kdd中任意一行与模型空间中的向量p的内积可以表示为:
(Kddp)(xi,xj,xs)=〈K(x;xi,xs)-K(x;xj,xs),p〉M=〈K(x;xi,xs),p〉M-〈K(x;xj,xs),p〉M
(A1)
冯波等[25]证明,走时敏感度核函数与模型空间向量的内积可以转化为波场空间中的内积:
(Kp)(xr,xs)=〈uq(xr,t;xs),up(xr,t;xs)〉T
(A2)
将(A2)代入(A1),有:
(Kddp)(xi,xj,xs)=〈uq(xi,t;xs),up(xi,t;xs)〉T-〈uq(xj,t;xs),up(xj,t;xs)〉T
(A3)
(A4)
其中λdd(x,T-t;xs)由如下双差走时伴随震源产生:
(A5)
顺序计算(A3)及(A4)式,无需显式计算和存储敏感度核函数及Hessian矩阵,可以直接获得Hessian向量积。
