基于三参数威布尔函数法的光电器件寿命快速评估模型及其应用
2021-03-22张建平
张建平,张 蓓
(1.上海电力大学能源与机械工程学院,上海 200090;2.上海理工大学机械工程学院,上海 200093)
光电器件具有可靠性高、寿命长、环境适应性好、耗能低等优点,应用范围十分广阔,涉及军事、航空航天领域及民用领域[1-2]。随着科学技术的发展、制造业水平的大幅度提高,光电器件性能的不断提升使得产品可靠性评估与寿命估计成为棘手问题[3-4]。如何基于加速寿命试验建立可靠快速的预测模型并获得寿命信息以加快产业化进程成为亟待解决的技术瓶颈。
国内外学者在加速退化试验(Accelerated Degradation Test,ADT)方面都进行了大量研究,目前主要有两种退化建模方法被广泛应用:退化轨迹曲线方法[5-7]和基于退化量分布方法[8-9]。前者的核心是依据合理的统计信息或物理模型来确定退化轨迹函数,而后者则是对多个产品在每一测量时刻的退化量的分布规律进行建模。Xiang等[10]提出了一种量子加权门控递归单元神经网络,完成了旋转机械的性能退化轨迹的预测。尤琦等[11]结合时序模型对退化轨迹曲线自拟合性强的优点,提高了产品可靠性评估与寿命预测的稳健性,并通过试验验证其有效性。夏云云等[12]提出一种对光参量呈非单调下降规律的LED灯珠可靠性进行评价的方法,通过对光通维持率退化数据进行拟合,发现利用其指数叠加形式的退化模型效果优于指数模型。Law等[13]利用不同类型LED在不同相对湿度条件下的亮度衰减数据,建立了基于湿度的LED退化轨迹模型并提出了利用湿度指数定量测量水分侵入影响的实用估算方法。Zheng等[14]对基于性能退化量的交流接触器进行电寿命分布特性分析,并进行电寿命试验完成可靠性评估。谷梦瑶等[15]提出了多退化变量下基于灰色生成率序列的相似性寿命预测方法,通过陀螺仪剩余寿命预测的实例,对所提方法的合理性和有效性进行了验证。Park等[16]提出了三种无需任意假设退化模型即可直接推断寿命分布的方法,并通过OLED实例和仿真表明方法的可靠性。Hao等[17]基于Nelson定律采用等累积退化量和等累积失效概率的模型,得到了不同应力下的等效试验时间,并用极大似然函数估计参数完成了对LED灯的寿命预测。
基于退化轨迹拟合建模方法具有参数估计容易、便于工程应用等优点,但是大多存在模型精度相对不高、计算效率低等问题。为此,本文针对具有亮度显性指标的光电器件构建了一种新的寿命快速评估模型:根据试验样品在多组加速应力下的亮度衰减特征规律,并结合加速应力与寿命之间的关系,直接得到了器件在常规工作应力下的性能退化规律,实现了寿命的快速评估。为实现该模型的应用,以国内一款真空荧光显示器(Vacuum Fluorescent Display,VFD)寿命评估为例,通过开展加速退化试验对模型进行验证及精度评价。
1 模型的构建
加速寿命快速评估模型构建思路如下:(1)采用三参数威布尔函数拟合多组亮度衰减数据,利用右逼近法估计参数,获得每组加速应力下的拟合公式;(2)结合加速因子将加速应力下亮度衰减拟合公式直接转化为常规应力下的公式,计算得出正常工作寿命。
1.1 基于威布尔函数的亮度衰减公式
对于恒定应力加速寿命试验,假设在加速应力Si(i=1,2,…,N)下第k(k=1,2,…,ni)个试验样品,在tj(j=0,1,2,…,Mi)时刻的亮度记为Lik(tj),则该时刻ni个试验样品的平均亮度Li(tj)为:
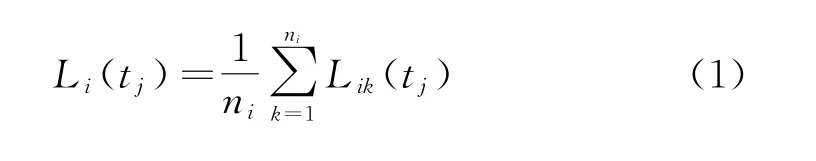
由此,通过式(1)可得到每组应力下试验样品平均亮度衰减数据(tj,Li(tj))。
三参数威布尔函数是在可靠性工程中广泛应用的连续性函数,函数式有三个参数能反映多个因素对函数的影响,所以具有形态丰富的曲线,其函数公式为:

式中:mi、ηi、t0i分别为待求的形状参数、尺度参数和位置参数。
令Fi(t)=1-Li(t)/Li0,根据式(2),则在加速应力Si下的亮度衰减公式可表示为:
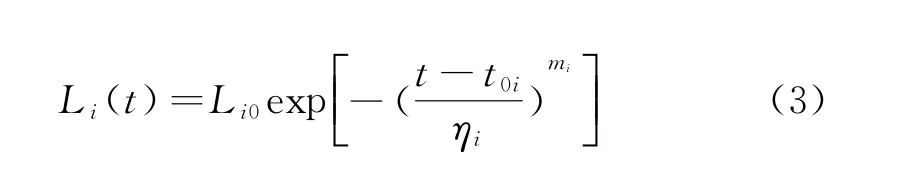
式中:Li0为产品的初始亮度;Li(t)为产品在t时刻的亮度。这里采用由三参数威布尔函数转化得到的亮度衰减公式(3)来拟合各加速应力下的试验数据。右逼近法是在最小二乘法的基础上改进得到的一种更为精确的参数估计方法,式(3)中的威布尔三参数采用右逼近法[5]来获得。
1.2 加速时间与常规时间的折算
针对退化型失效,如光电元器件性能的衰退、机械部件磨损、药品效力的降低、绝缘材料老化等[18],产品承受的加速应力为S,第i级加速应力水平记Si,正常应力水平记为S0,在S0、Si下,则时间比τi=t0/ti,称为加速应力水平对正常应力水平的加速系数,简称加速系数,表示性能指标的退化量相同时所经历的时间之比[19-20]。
不同应力水平下产品的加速时间与正常应力下的工作时间可以通过加速系数τi来折算,具体的关系表达式为[21]:
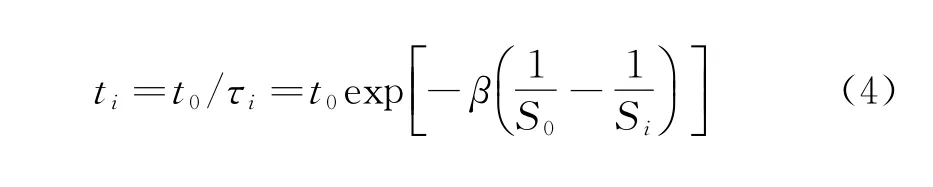
式中:t0、ti分别为正常应力S0和加速应力Si下的测试时间;β为加速方程参数。需指出的是,加速方程是表述产品寿命分布参数与应力水平之间的关系式,β可通过利用加速寿命试验数据和概率统计方法计算得到[19,21]。
1.3 常规寿命计算
结合式(3)和式(4),可得到加速应力Si所对应的正常工作应力下的亮度衰减公式,可写为:
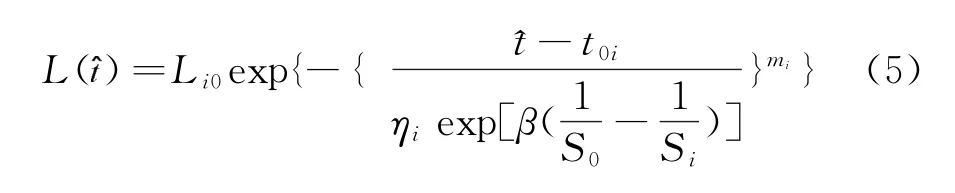
设Lf为失效亮度,在式(5)中令L()=Lf,则可计算出光电产品在正常工作应力下的平均寿命μi,即为:

为了降低由亮度衰减模型计算的寿命误差,对由式(6)得到的Si下常规工作寿命μi(i=1,2,…,N)取平均,即有:
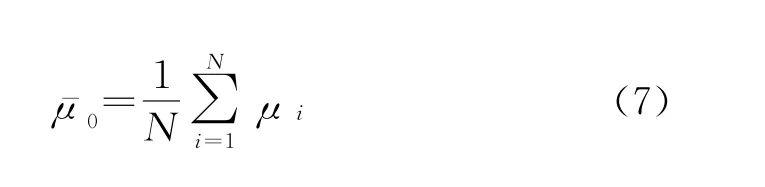
式中:μ-0为产品在正常应力S0下的寿命。
1.4 建模流程

最后,将失效亮度Lf代入式(5)可计算出由每组加速应力推得的正常工作应力下的平均寿命μi(i=1,2,…,N),利用式(7)便可完成常规寿命μ-0的预测。具体的寿命快速评估模型流程见如图1。
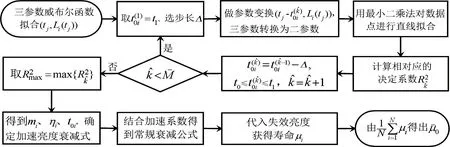
图1 寿命快速评估模型流程图Fig.1 Flow chart of rapid life assessment model
2 模型的应用
VFD是一种利用电子轰击荧光粉致使自身发光的电子显示器件,由发射电子的阴极(直热式,统称灯丝)、加速控制电子流的栅极、玻璃基板上印上电极、表面涂覆有荧光粉的阳极等构成[22]。
为评价寿命快速评估模型的精度,本文以真空荧光显示器VFD 为试验对象,开展了加速应力退化试验,采集样品亮度衰减的实测数据,并利用寿命快速评估模型得到了样品的常规寿命。
2.1 VFD试验方案设计
2.1.1 应力的选择及样品的投放
VFD产品的寿命主要受阴极灯丝温度的影响,所以试验中选取温度作为加速应力,并采用四组恒定加速退化试验对VFD 产品进行性能退化研究,寿命试验台如图2所示。
选取80个样品,且在保证失效机理不发生变化的前提下确定了以下四个加速应力水平:S1=1023.00 K,S2=1055.56 K,S3=1087.85 K,S4=1123.33 K。在进行性能加速退化试验时,每个应力水平下投放20个样品,即ni=20(i=1,2,3,4)。此外,S0=923.15 K为正常工作温度应力。
2.1.2 失效标准和试验终止时间
在正常测试条件下,目前VFD 行业认同亮度作为寿命特征,其测试位亮度低于最低亮度标准(350 cd/m2)的60%,即210 cd/m2时认为该产品失效。

图2 VFD寿命试验台Fig.2 VFD life test bench
2.2 亮度衰减试验数据
根据上述提出的试验方案对VFD 开展四组恒定应力加速退化试验,在每个加速应力Si(i=1,2,3,4)下每个测试点个数分别为:M1=22,M2=25,M3=11,M4=7。采集记录的亮度衰减实测数据(tj,Li(tj))分别列于表1、表2、表3和表4,其中Li(tj)为实测值,L-i(tj)为根据拟合公式计算的亮度。
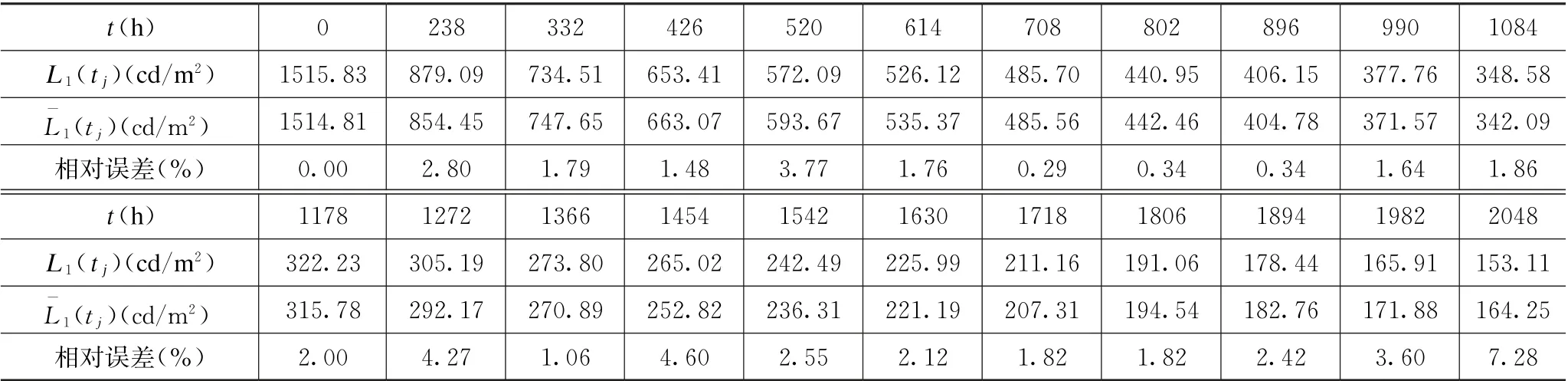
表1 S1下试验样品的平均亮度随时间变化数据Tab.1 Data of the average luminance of test samples varying with time under S 1
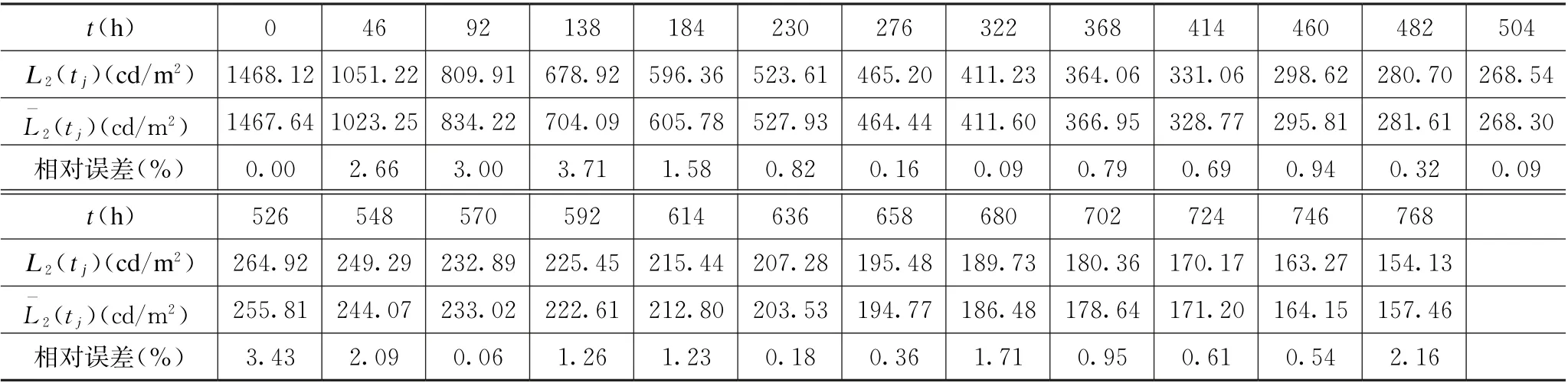
表2 S 2下试验样品平均亮度衰减实测数据Tab.2 Measured data of average luminance attenuation of test samples under S 2

表3 S 3下试验样品的平均亮度随时间变化数据Tab.3 Data of the average luminance of test samples varying with time under S3

表4 S 4下试验样品平均亮度衰减实测数据Tab.4 Measured data of average luminance attenuation of test samples under S 4
2.3 恒定加速应力下亮度衰减拟合
将每个温度应力Si下试验测得的平均亮度随时间变化的数据(tj,Li(tj)),分别代入亮度衰减公式(3)进行拟合,结合右逼近法便可以计算出形状参数mi、尺度参数ηi和位置参数t0i,计算结果列于表5。为验证拟合效果,将每组加速应力下的工作时间tj代入式(3)可得到亮度L-i(tj),并计算相对误差,结果分别一并列于表1—表4。经过计算,温度应力S1、S2、S3、S4下亮度平均误差分别为2.26%,1.18%,2.55%,6.39%。由此看出,三参数威布尔右逼近法拟合误差小,确保了产品寿命的准确评估。
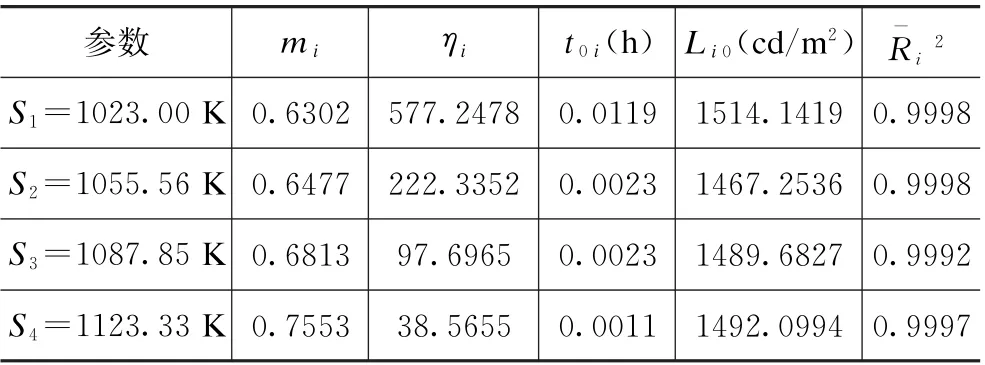
表5 各加速温度应力下VFD试验样品的相关参数Tab.5 Relevant parameters of VFD test samples under each accelerated temperature stress
各应力下的VFD 试验实测点与对应的亮度衰减拟合曲线绘于图3。由图3可以发现:随着加速应力的增大,VFD的亮度衰减幅度加大、速度加快,四条曲线准确反映出了光电器件亮度衰减的特性;亮度试验数据大致落在拟合曲线上,且决定系数都非常接近于1,说明拟合效果较好。此外,由表5可知,四组加速应力下的形状参数分别为:m1=0.6302,m2=0.6477,m3=0.6813,m4=0.7553,其加权平均值为m=0.6786,四个形状参数非常接近,说明退化轨迹形状基本一致,这表明了多组加速寿命试验过程中VFD试验样品的失效机理不变[23],验证了试验产品未发生异常失效,实测数据可靠、有效。
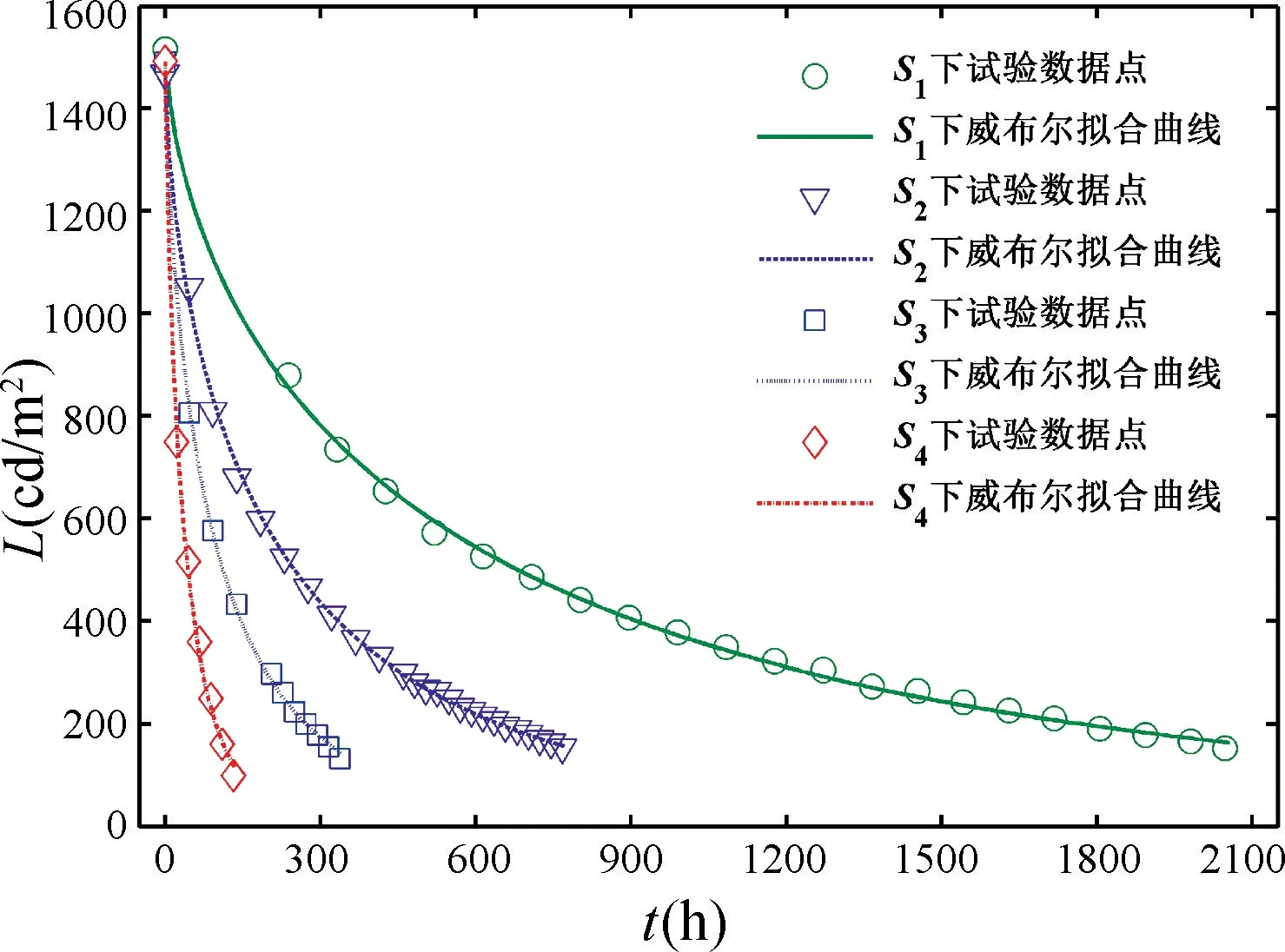
图3 各应力下的试验数据点与对应的拟合曲线Fig.3 Test data points and corresponding fitting curves at various accelerated stresses
根据表5中各加速温度应力下VFD试验样品的相关参数及亮度衰减公式(3),结合失效亮度Lf=210 cd/m2可推得四个应力条件下的加速寿命,结果列于表6。

表6 每个应力下的加速寿命Tab.6 Accelerated life under each stress
2.4 正常应力下亮度衰减曲线
本文试验产品与参考文献[21]试验产品是同环境下试验的同一批次产品,具有相同的产品性质、试验条件及试验方法。因此,在计算出式(3)威布尔三参数mi、ηi、t0i后,取该文献中的β=30940.94代入式(5),可以得到四组加速应力推至正常工作温度应力下的VFD亮度衰减公式,如表7所示。

表7 常规工作应力下VFD亮度衰减公式Tab.7 VFD luminance attenuation formula under conventional working stresses
基于表7,图4给出了正常工作温度应力下的亮度衰减曲线。可以直观地看出:四条曲线呈现非线性的下降趋势且基本重合,表现出一致的亮度衰减特性。此外,每组加速应力下的加速系数乘以测试点时间,并与此时刻测试的亮度形成数据点,发现由加速应力转换正常应力后的亮度衰减曲线与该数据点吻合程度高,说明确定的加速应力范围合理,不会引起新的失效机理,四个正常工作应力下的亮度衰减公式均准确揭示VFD亮度随时间变化的规律。
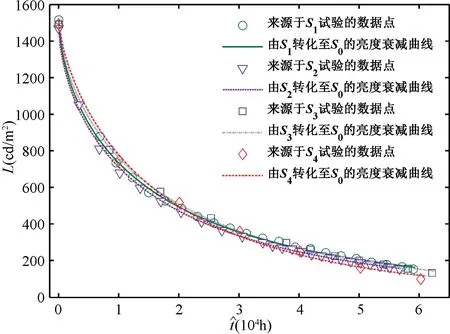
图4 正常工作应力下的亮度衰减曲线Fig.4 Luminance attenuation curves under normal working stress
2.5 常规寿命的计算
对于VFD令Lf=210 cd/m2,利用表7中的四个亮度衰减公式,可分别计算出正常工作应力下的寿命:μ1=4.48014×104h,μ2=4.15599×104h,μ3=4.19160×104h,μ4=3.69255×104h。为了降低计算误差,将μi(i=1,2,3,4)代入式(7),可得到平均寿命为:μ-0=4.13007×104h。
3 模型的精度
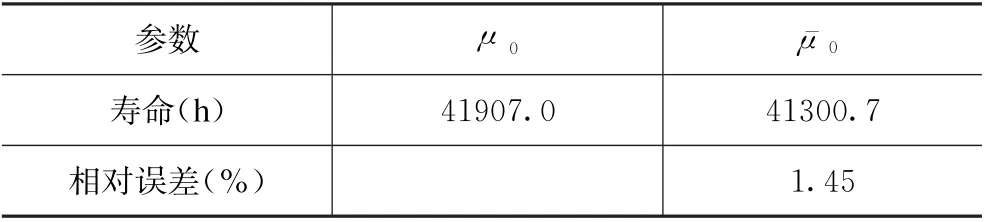
表8 寿命对比Tab.8 Life comparison
4 结论
结合亮度衰减特性及加速退化试验,通过引入右逼近法参数估计及加速系数,建立了寿命快速评估模型,并成功应用于VFD的寿命评估,结论如下:
(1)相较于VFD 传统40000 h左右的常规寿命试验,四组加速退化试验下的测试时间缩短至常规试验的5%以下,大幅度加快了寿命试验进程,降低了试验和试制成本,提高了光电产品新品研制的速度;
(2)加速应力下的三参数威布尔亮度衰减公式直观地反映了器件亮度性能随时间、应力的变化,将其推至常规应力下时亮度退化表现出高度的一致性,表明本文模型不论在加速应力下还是常规应力下均能客观地揭示产品亮度的衰减特性,具有较高的普适性;
(3)四组加速应力下模型的拟合结果与试验实测的亮度数据的平均相对误差仅为3.10%,且基于此估算的寿命值与文献参考值相比误差小于3%,表明建立模型的思路正确可行,并具有较高的预测精度;
(4)从VFD寿命预测整体上看,寿命快速评估模型能够有效规避传统常规寿命试验测试周期长的弊端,在保证试验数据信息量大的前提条件下仍能有效快速地获得寿命信息,进一步丰富了光电产品的寿命预测理论体系。
