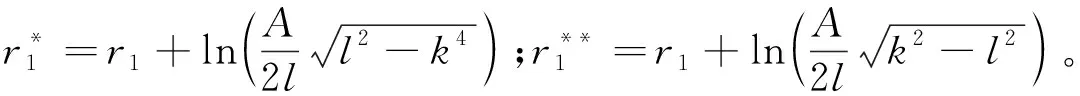(2+1)维非线性演化方程的显示解

刘小平

(电子科技大学中山学院 计算机学院,广东 中山 528406)

寻求物理、数学上有重要意义方程的显示解一直是热门话题，现已形成许多成熟的方法，比如Hirota直接法[1-5]、穿衣方法[6-12]、Riemam-theta 函数与直接法相结合的方法[13-16]。其中，Hirota直接法提供了一个强有力的获得非线性演化方程的方法。此方法主要以Hirota双线性公式为基础，一旦建立该方程的双线性形式，就可以得到该方程的孤子解、奇异解、有理周期解。

本研究采用Hirota双线性方法，讨论如下(2+1)维非线性演化方程的显示解，包括孤子解、奇异解、有理周期解：

(1)

本研究利用规范变换和Hirota双线性算子的特性，得到方程(1)的双线性形式，再利用Hirota直接法得到方程(1)的孤子解和奇异解，最后借助新的变换求出方程的有理周期解。

1 (2+1)维非线性方程的双线性形式

首先，引入双线性算子D：

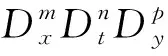
当算子D作用在指数函数上时有更好的特性：

式中：ξj=kjx+wjt+ljy+ri，i=1，2。

更一般的情况：G(Dx，Dt，Dy)eξ1eξ2=G(k1-k2，w1-w2，l1-l2)eξ1+ξ2。令

u=2(lnf)xx，

(2)

把公式(2)代入方程(1)可得

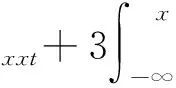
(3)

对式(3)两边关于x积分一次，并取积分常数为0，可得

-4·2(lnf)xt+3(2 lnf)yy+2(lnf)xxxx+3[(2(lnf)xx]2=0。

(4)

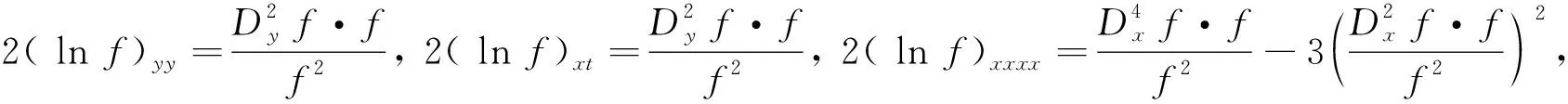
(5)

2 (2+1)维非线性方程的孤子解和奇异解

本部分利用双线性方法构造方程(5)的解，进而获得方程(1)的解。利用文献[1]提出的扰动法：

f=1+εf1+ε2f2+ε3f3+L，

式中：ε是小参数。

2.1 孤子解

2.1.1单孤子解

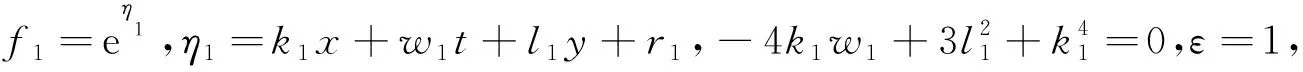
f=1+eη1。

利用式(2)得

(6)

2.1.2二孤子解

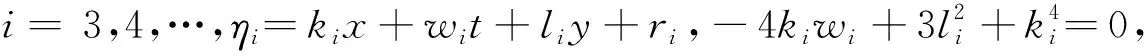
式中:

(7)

利用式(2)可得二孤子解

(8)

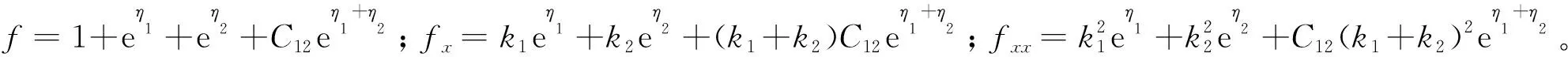
类似地，可以得出N-孤子解。

2.2 奇异解

2.2.1单奇异解

令f=1-eη1，可以得到单奇异解

(9)

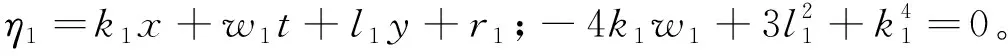
2.2.2二奇异解

令f=1-eη1+η2+C12eη1+η2，利用式(2)可得二奇异解

(10)

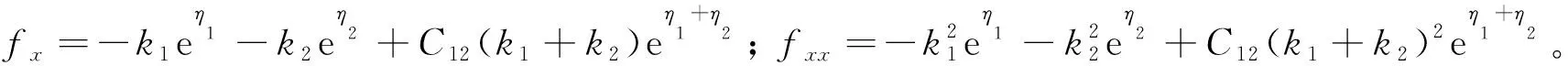
3 有理周期解

令

f(x,y,t)=e-η1+Acosη2+Beη1，ηi=kix+wit+liy+ri,i=1,2。

(11)

把式(11)代入式(5)比较e-η1、eη1、cosη2、sinη2，使得系数为0，可得

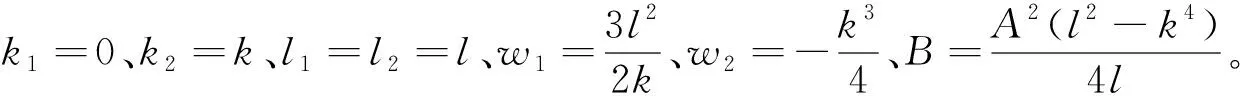
把上述结果代入式(11)，可得以下两种情况，不妨记为f1、f2：

借助变换(2)可得原方程(1)的解为