分层岩土介质振动响应的传递矩阵法求解

毕战歌， 刘 军，2

（1.河海大学土木与交通学院安全与防灾工程研究所，南京 210098；2.河海大学岩土力学与堤坝工程教育部重点实验室，南京 210098）

分层岩土介质的动态力学特性研究一直是国内外学者关注的热点之一. 在岩土工程、防护工程和爆破工程中，分层岩土介质弹性半空间的地表振动响应研究具有重要工程意义. 许多学者在分层介质的动力奇异解问题上做了研究，Franssens［1］导出了多层半无限介质的平面问题的时域奇异解；Apsells［2］和Kauselle［3］分别导出了多层半空间问题的频域奇异解；孙成禹和张立［4］求解了与水平面呈任意夹角的表面线源作用于弹性半空间的拉普拉斯-傅里叶双积分变换解；奚亚男［5］在势函数理论基础上，运用Laplace变换、傅里叶-贝塞尔积分等数学手段，得出了地基表面各点位移的形式解. 许多学者对层状介质的振动响应问题从不同的角度上进行了研究. Piotr和Neves［6］等提出了一种基于小波变换的方法来分析和优化多层介质在移动荷载作用下动力响应的方法. 在试验研究方面，Wang［7］等利用SHPB试验装置，建立了一种适用于层状介质动态性能研究和数据分析的试验方法. 在数值模拟方面，Kumar［8］等利用考虑投射边界的有限元法，对土-岩和岩-岩地基系统在竖向振动模式下对块体基础动力响应的影响进行了研究.

本文在前人研究的基础上，求得了任意方向脉冲点源荷载作用下分层岩土介质地表垂向振动位移的数值解析表达式，进行了落锤冲击水泥公路试验，用ANSYS/LS-DYNA进行数值模拟，使用Mathematica软件对本文提出的方法进行编码数值计算，将三种方法得到的地表垂向振动位移衰减曲线进行对比分析，结果可为工程中分层岩土介质的动态响应相关计算提供一定的理论参考.

1 传递矩阵的推导

本文采用如图1所示的弹性半无限空间上覆3层均匀、各向同性的分层弹性半空间岩土介质模型，在该模型表面作用任意方向的集中脉冲点源荷载P0F(t) .

图1 任意方向脉冲点源荷载作用下分层弹性半空间岩土介质模型Fig.1 Layered elastic half space geotechnical model under impulsive point source load in arbitrary direction

1.1 基本方程

本文讨论的情况不计体力，则分层弹性半空间岩土介质模型任意一层内的每一点都满足弹性波动力学的基本方程：

1.2 积分变换

该研究问题中包含时间t 这一实变量函数. 在时域中进行一些运算并不容易，但若将时间t 作拉普拉斯变换，即可将时域中的问题转换为复数域的问题，并在复数域中作各种运算，再将运算结果作拉普拉斯反变换来求得时域中的相应结果，这就是引入拉普拉斯变换的一个主要优点.

对公式（1）进行关于时间t的Laplace变换，得到：

对公式（4）再进行Hankel变换，可得：同理，对本构关系式（2）和（3）也进行Laplace-Hankel联合积分变换，可得应力的积分变换形式：

1.3 Cayley-Hamilton定理

将经过积分变换后的基本方程和本构方程合并，写成常微分方程组的形式：

其中：

根据文献［9］中关于常微分方程组的解答并结合本模型，可得i=4，故有4个方程解的形式：

可以看出，指数矩阵即描述任意深度z的状态向量与该层表面处的状态向量间关系的传递矩阵. 只要求解出该指数矩阵，就可以求得Ui(ξ,z,s) .

关于该指数矩阵的求解，根据凯利-哈密尔顿（Cayley-Hamilton）定理［10］，可以得到e[zDi(ξ,s)]的特征方程为：

求解上述方程组，得：

代入可得到传递矩阵：

式中：

为了方便起见，忽略式中的i，各符号意义同前. 根据推导出的传递矩阵，Ui(ξ,z,s)就可以写成如下形式：

1.4 边界条件

分层岩土介质的层间边界处满足连续介质力学的假设，所以边界处应力位移是连续的，即：Ui(ξ,hi-1,s)=Ui-1(ξ,hi-1,s). 利用该边界条件，再借助Ui(ξ,z,s)的公式，可建立起地表上状态向量与分层岩土介质及其下半无限介质内状态向量的关系式：

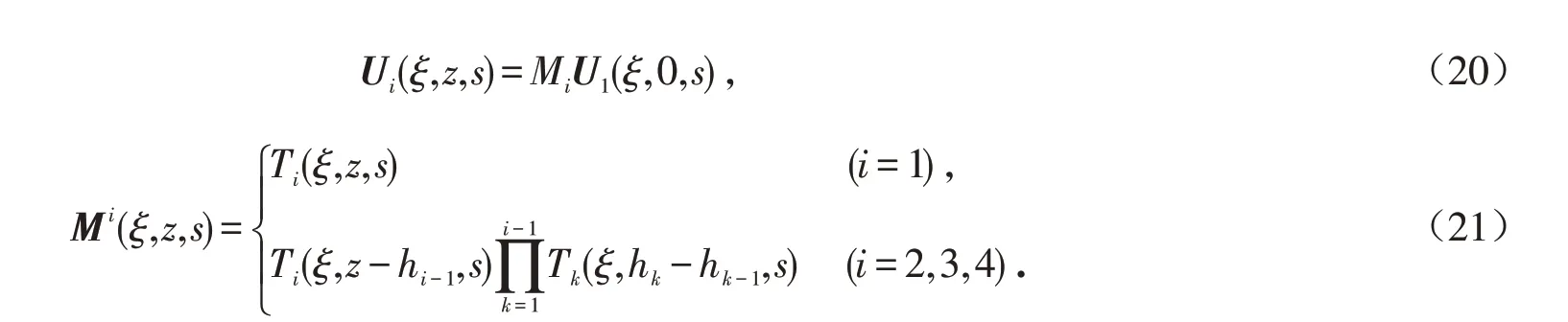
1.5 矩阵分块法

将边界条件代入关系式，利用矩阵分块法［12］求得：

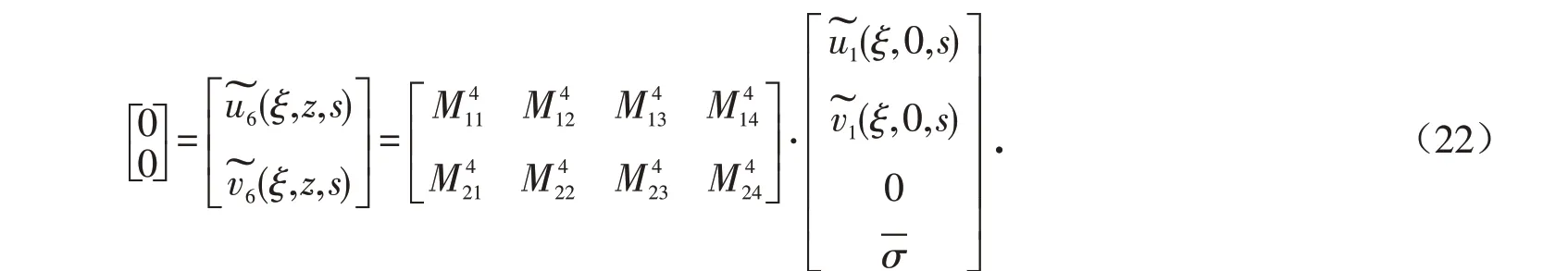
化简，得：

1.6 脉冲荷载及幅值确定

在该研究模型中，荷载的形式是任意方向的脉冲点源荷载，其形式如下：

对上式进行Laplace和0阶Hankel变换：

在上述表达式中，P0为脉冲荷载的幅值. 解答在实际运用中，需确定脉冲幅值P0的大小. 通过量纲分析可知P0的单位为N. 脉冲荷载幅值考虑采用脉冲触地瞬间的最大冲击力. 分析对比若干种冲击力的计算方式后，决定采用Hertz碰撞理论［13］进行求解. 触地冲击这一过程可看作两弹性球体间的弹性碰撞，碰撞时的最大冲击力P0可通过下式计算：

式中：m、M分别为两弹性球A、B的质量；V为碰撞前的速度；r、R分别为两弹性球的半径；E1、E2分别为两弹性球的弹性模量；v1、v2为两弹性球的泊松比. 假定冲击体为A，地面为B，地面B的质量M和半径R可看作无穷大，上式可简化为：

式（31）分母中，泊松比与弹性模量的比值大小相比较两弹性模量的比值可忽略不计，因此最大冲击力P0的计算公式可简化为：

2 落锤冲击水泥公路试验

以落锤冲击地面作为振源，水泥公路作为试验对象. 为尽可能减少外界干扰对试验的影响，同时确保试验人员的人身安全，最终选择南京市鼓楼区虎踞路某围闭施工的道路区间进行. 水泥路面自上而下总共由四部分组成，依次为10 cm 厚水泥路面、10 cm 水稳碎石基层、10 cm 三合土底基层及天然红土基层，如图2所示，落锤及各土层材料物理力学参数如表1所示.

图2 水泥路面结构Fig.2 Cement pavement structure

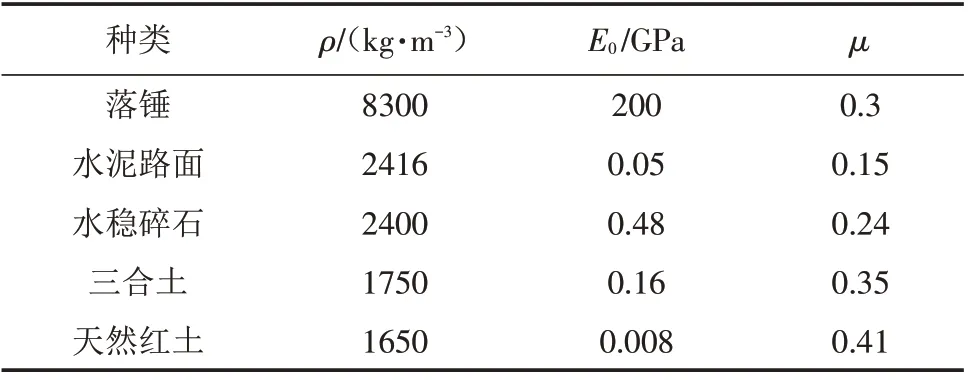
表1 材料物理力学参数Tab.1 Physical and mechanical parameters

2.1 试验设备及方法

试验的设备主要由落锤冲击加载装置及振动监测装置两部分组成. 落锤冲击加载装置由三脚支撑架起吊装置和落锤组成，振动监测装置采用加拿大Instantel公司生产的Minimate-Pro4振动和过压监测仪. 试验共计取监测点12个，监测点编号按距冲击点距离的远近依次为P1～P12，每个监测点之间的距离为0.3 m. 其中，监测点P1距落锤冲击点0.3 m. 按测点布置图3将三向检波器分别放置在对应位置，并将三向检波器径向指向振源方向，利用石膏将三向检波器与地面刚性连接，待石膏凝结硬化后开始试验，如图4所示.

图3 测点布置示意图Fig.3 Layout of measuring points

图4 三向检波器与地面刚性连接Fig.4 The three-way geophone rigidly connected with the ground

采样频率设置应遵循奈奎斯特定理，即为保证离散数字信号能够不失真地恢复到连续的模拟信号，采样频率应不小于信号中最高频率的2倍. 在实际应用中，采样频率通常设定为信号最高频率的5～10倍，为了更加准确地研究振动波形，采样频率设为信号最高频率的10倍以上. 故试验振动波形监测装置的采样频率设为2048 Hz. 根据现有试验条件，在保证安全的前提下，落锤冲击试验的最终下落高度定为1.2 m，得到的振速时程曲线如图5所示（由于测点多，此处取测点P7的波形图用以展示）.

图5 1.2 m冲击高度振速时程图（测点：P7）Fig.5 Time history diagram of vibration velocity at 1.2 m impact height（measuring point：P7）

2.2 数据处理

为了用该计算方法来验证该试验并与试验结果相比较分析，我们需要得到地表垂向振动位移与距振源距离之间关系的变换曲线，所以需要对测得的速度时程曲线进行积分处理. 若直接积分，曲线会出现较为严重的漂移现象. 因此，还需要通过基线校正来解决该问题. 采用DPLOT 曲线处理软件对速度时程曲线图进行处理，通过“Generate->Integrate a Curve”指令对速度时程曲线积分得到位移时程曲线，再通过指令“Edit->Remove Trend”并选择刚得到的位移时程曲线来对位移进行一次线性基线校正，即可得到不漂移的位移时程曲线. 利用该方法对P1～P12 监测点的振动速度时程曲线进行处理，然后提取沿各测点位移时程曲线中的位移峰值，可得到位移随距振源距离变换的曲线，如图6所示.

图6 地表垂向振动位移与振源距离关系曲线Fig.6 Relationship curve between surface vertical vibration displacement and vibration source distance

3 ANSYS/LS-DYNA数值模拟

为了与试验结果相比对，采用ANSYS/LS-DYNA 软件建立了4 m×1 m、厚度为10 cm 的分层岩土介质落锤冲击振动模型，并模拟其受2.5 kg钢制落锤冲击的工况. 设置总计算时间为3.6×10-3s，动画的输出间隔为5×10-5s，因此共输出约75 帧. 为了让观测点（图7 中黄色点所示）输出更多的数据，采用DATABASE_HISTORY_NODE_SET 和DATABASE_NODOUT，设置观测点的输出间隔为1×10-6s，因此每个点可以输出3600 个数据. 在落锤的冲击作用下，模型应力响应如图8所示.

图7 分层岩土介质模型的数据观测点Fig.7 Observation points of layered rock and soil media model

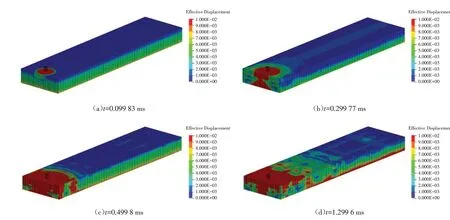
图8 不同时刻的位移云图Fig.8 Displacement maps at different times

根据模拟结果，选取距冲击点0.5 m至3.8 m之间的12个监测点P1～P12，各测点距离及垂向振动位移峰值整理如表2所示.

表2 垂向振动位移峰值Tab.2 Peak value of vertical vibration displacement

4 数值实施及计算

针对试验的工况，利用表达式（25）进行数值计算，用来考核该解答数值化实施的可行性. 从表达式（25）可以看出：无穷域的Hankel 变换和Laplace 变换将直接影响解答数值实施的精度，所以找到相应的快速有效的计算方法将对数值化实施的可行性至关重要. 这里，选取两种解决无穷域积分的数值计算方法，即快速Hankel 变换［14］和改进后的Durbin 方法［15-16］. 利用这两种方法分别对表达式（25）中的无穷域Hankel变换和Laplace变换进行处理，这样对表达式（25）进行的数值计算的实施将会变得更加方便，而且公式中矩阵的阶数为4 阶，因此对工作量的增加将会比较有限. 利用Mathematica 软件编写代码数值计算，对结果进行数据处理，得到地表垂向振动位移与振源距离关系曲线，结合现场实验的结果绘制得到对比图（图9）.

从图9可以看出，利用该数值方法的计算结果与数值模拟结果更相近，二者与试验实测值的误差均未超过1.7 mm/s，得到的衰减规律均与试验实测的结果衰减规律基本一致，故可证明该数值分析方法实施的可行性，结果可为相关工程计算与分析提供参考.

试验得到的垂向振动位移衰减曲线存在明显的起伏现象. 这是因为落锤作为试验中脉冲载荷的输入形式，实质上可视为均布的一系列脉冲点源的集合. 一方面，对地面某测点而言，各脉冲点源相应的相位是互异的，即不同点发出的波动有相位差，振动波传至该点合成时根据相位相同或不同分别产生叠加和抵消作用，致使垂向振动位移衰减曲线出现起伏；另一方面，应力波在层状地基中传播时，在交界层面将发生反射、折射，而反射波和由振源传出的振动波发生干涉也会导致衰减曲线出现起伏.

图9 地表垂向振动位移衰减曲线对比Fig.9 Comparison of attenuation curves of surface vertical vibration displacement

5 结论

采用理论模型建立、试验研究、数值模拟及数值算法编制与程序开发相结合的研究思路，对分层岩土介质的振动响应研究进行了系统深入的研究，主要成果如下：

1）在前人研究的基础上，利用Laplace-Hankel 联合积分变换和传递矩阵法给出了与水平面呈任意夹角的点源脉冲荷载作用下弹性半空间分层岩土介质地表垂向位移的数值解析式.

2）进行落锤冲击水泥公路试验和ANSYS/LS-DYNA 软件进行数值模拟，得到距冲击源不同位置处地表各点的垂向振动位移，并绘制出垂向振动位移衰减曲线，与提出的数值解析方法得到的计算结果进行对比分析. 结果表明，将传递矩阵法应用到分层岩土介质地表振动响应问题研究中，能较好地反映任意方向脉冲激励下地面振动的衰减过程，且计算方法简洁，易于应用.

3）只给出了任意方向点源脉冲荷载作用下弹性半空间分层岩土介质地表的垂向位移表达式，对于其他荷载类型作用下的振动位移求解可以通过荷载函数与脉冲响应的卷积得到，该研究成果可为分层岩土介质在冲击荷载下的地表振动规律分析提供一定的指导意义.