虚拟现实空间中角度量参数深度对放置任务操作时间的影响

邓成龙,蒯曙光，2，3

(1.华东师范大学 脑科学与教育创新研究院，上海 200062； 2.华东师范大学 心理与认知科学学院，上海 200062； 3.华东师范大学 上海市心理健康与危机干预重点实验室，上海 200026)

1 引言

近几年随着虚拟现实(VR)技术的快速发展，VR已经广泛应用于游戏、仿真、训练、教育等领域[1-6]。由于深度是三维空间的重要特征之一，虚拟物体可能出现在不同的深度，因此了解深度如何影响人的操作表现非常重要，研究结果将帮助VR应用的设计者评估任务难度，提高用户体验。

一些研究者在三维空间中探索了深度因素，然而深度如何影响人的操作表现还不完全清楚，操作行为模型的建立还没有达成一致[7-10]。Kopper等人(2010年)在现实环境中让被试站在距离大屏幕不同深度(1 m,2 m,3 m)的位置，通过手持具有位置追踪的手柄配合射线的方法点击屏幕上连续出现的两个圆形目标。他们使用线性量表示移动距离和目标的大小。他们发现随着深度的增加，操作时间增加，并且使用费茨定律不能很好地拟合线性数据。他们将线性参数转换成角度参数，并对费茨定律进行修正。新的角度参数模型不包含深度参数，也能够很好地解释人的操作表现，他们认为角度参数包含了深度的影响[7]。但是Kopper等人采用的不是沉浸式环境，与VR场景存在不同。Janzen等人(2016年)采用类似的装置完成远距离的点击任务，但是他们要求被试佩戴立体眼镜提供沉浸式视觉，同时改变人与屏幕的物理深度(1.1 m,2.2 m,3.3 m)和目标的感知深度(1.1 m,2.2 m,3.3 m)。他们同样使用线性参数并且发现物理深度和感知深度都对人的操作时间造成了影响，但是Kopper等人(2010年)提出的角度模型并不能很好地解释他们的数据。他们发现Welford模型能够很好地拟合线性数据，然而角度量数据没有提高模型的拟合结果[8]。该结果也得到了其他研究的支持[10]。在近期的一项VR研究中，Qian等人(2017年)使用眼控和头控操作完成点击任务，他们采用线性参数并将目标深度设置为5 m，7 m和9 m。他们的结果显示操作时间随着深度的增大而增加。他们使用费茨定律拟合角度量数据，与前两项研究使用的模型不同[9]。这些研究造成模型结果不一致的部分原因是当使用角度量表达参数时深度对人的操作表现的影响还不清楚。虽然参数的角度量公式包含了深度信息，但是这些研究都是在使用线性参数情况下探索深度的影响，并没有验证角度量参数是否完全包含了深度的影响。如果不完全包含，基于角度量的模型仍然需要加入深度参数，才能使得模型更准确。

在本研究中，我们使用手柄配合虚拟射线的操作方法将不同深度的光标放入目标内。手控操作是VR中最常用的交互方式，放置任务是VR中的常见任务[11-13]，比如将虚拟商品放入购物车中，因此基于两者的研究结果将具有广泛的适用性。我们分别使用线性量和角度量表示光标大小、目标大小以及移动距离。为了系统研究深度在两种参数表达方法中如何影响人类的操作表现，我们对光标的移动过程进行分析。在前期的研究中，我们将移动过程划分成三个阶段，发现每个阶段的影响因素不同[13]。本研究将参照前期研究的方法将光标的移动过程划分成加速阶段、减速阶段和调整阶段，详细分析深度对每个阶段的影响。

2 对象与方法

2.1 被试

一共34名在校大学生参与了本研究(19名女性，15名男性)，其中实验1包含17名参与者(10名女性，7名男性，平均年龄：22.0岁±2.5岁，平均身高：166.0 cm±6.8 cm)，实验2包含了17名参与者(9名女性，8名男性；平均年龄：22.0±2.4岁，平均身高：166.0 cm±6.9 cm)。他们的视力或者矫正视力正常，均为右利手，且均无认知与行为上的障碍，他们对实验目的不知情。完成实验之后，他们将获得一定金额的报酬。

2.2 实验仪器

本研究使用HTC VIVE虚拟现实设备，该设备包含一个头盔、两个无线手柄和两个光学位置追踪器(图1a)。头盔的单眼屏幕分辨率为1 080×1 200，重量350 g，最大刷新率为90 Hz，手柄重50 g。该系统能够实现对头盔和手柄在最大3 m(长)× 4 m(宽)范围内的位置追踪，定位精度1 mm。实验程序采用Unity 5.6.2软件编写，并运行在Dell Alienware计算机上，计算机配备NVIDIA GeForce TITAN显卡，Intel i7处理器和16G内存，确保了程序的刷新率稳定在90 Hz。

2.3 实验设计

本研究采用与我们先前的研究相同的虚拟场景和实验刺激，如图1所示。实验1和实验2分别使用线性量和角度量表示光标(红色小球)、目标(白色半透明大球)和移动距离的大小。本研究采用3深度(2 m，3 m，4 m)×3光标直径大小(实验1：0.12 m，0.24 m，0.36 m；实验2：2°，4°，6°)×2移动距离(实验1：0.7 m，0.15 m；实验2：20°，40°)× 3目标容差(实验1：0.1 m，0.2 m，0.3 m；实验2：2°，4°，6°)的被试内重复实验设计。目标容差为目标与光标的大小差异。光标和目标距地面的高度为1.5 m。每个实验包含5个区组，每个区组包含所有的54个自变量组合，自变量的所有水平组合顺序随机，每个实验总共包含270个试次。

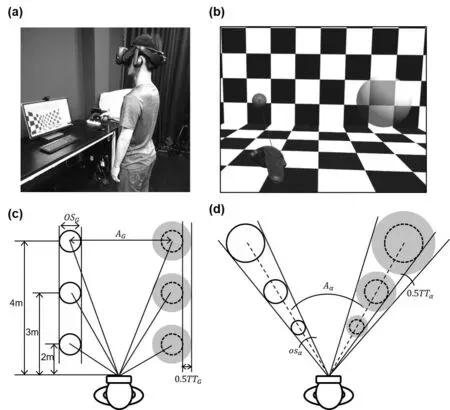
图1 实验设备与设计示意图。(a)实验设备和被试操作示意图；(b)实验场景和刺激图。左侧红色小球为光标，右侧白色半透明大球为目标；(c)线性量表示参数示意图；(d)角度量表示参数示意图。OS表示光标大小；A表示移动距离；TT表示目标容差。

2.4 实验过程

本研究得到了学校伦理委员会的批准。被试在实验开始之前先签订知情同意书，然后佩戴好VR头盔，手握手柄，站在指定的位置。在虚拟场景中，被试将看到左侧的黄色小球(光标)和右测的半透明的白色小球(目标)(图1)，然后将手柄上发出的虚拟射线指向光标，光标颜色从黄色变成红色，此时按下手柄背后的触发键即可选中光标。接着被试需要尽量快而准地将光标移入目标球内。在移动的过程中，触发键需要一直处于按下的状态。当被试将光标完全放入目标球内后，松开触发键，放下光标。如果光标没有完全放入目标球体内，程序将播放错误提示声音，然后进入下一个试次。在正式实验开始前，被试需要完成20个试次的练习，然后完成5个区组的测试，区组与区组之间有1 min的休息时间。

2.5 数据分析

在实验1中，一名被试的错误率较高(30%)被剔除，剩下16名被试的平均错误率为3.36±2.10%。在实验2中，由于一名被试的平均完成时间(2.49 s)显著高于其他被试的完成时间(1.17 s)，因此被剔除，最终有16名被试的实验数据被采用，他们的平均错误率为5.58±5.30%。错误的试次将不进入数据分析。

我们按照前期研究的方法对光标的速度轨迹划分成三个阶段：加速阶段、减速阶段和调整阶段(图2)[13]。在前期研究中，目标的深度为2 m，设定减速阶段与调整阶段分界点的速度低于2 m/s。在本研究中，我们按照一定的比例，设置深度3 m和4 m对应的减速阶段和调整阶段的分界点速度分别<3 m/s和4 m/s。我们对操作时间进行3(深度)×3(移动物体大小)×2(移动距离)×3(目标容差)的被试内重复测量方差分析，并采用 Greenhouse-Geisser方法对不满足球形假设检验的结果进行校正。

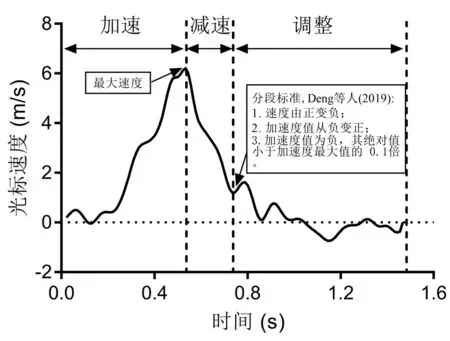
图2 三阶段划分标准示意图

3 结果

3.1 深度对操作时间的影响

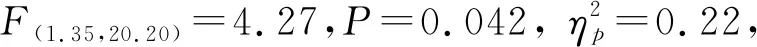
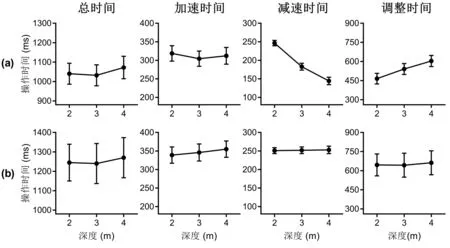
图3 深度对总操作时间和三个阶段的操作时间的影响。(a)实验1；(b)实验2。

3.2 光标大小、移动距离和目标容差对操作时间的影响

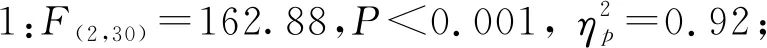
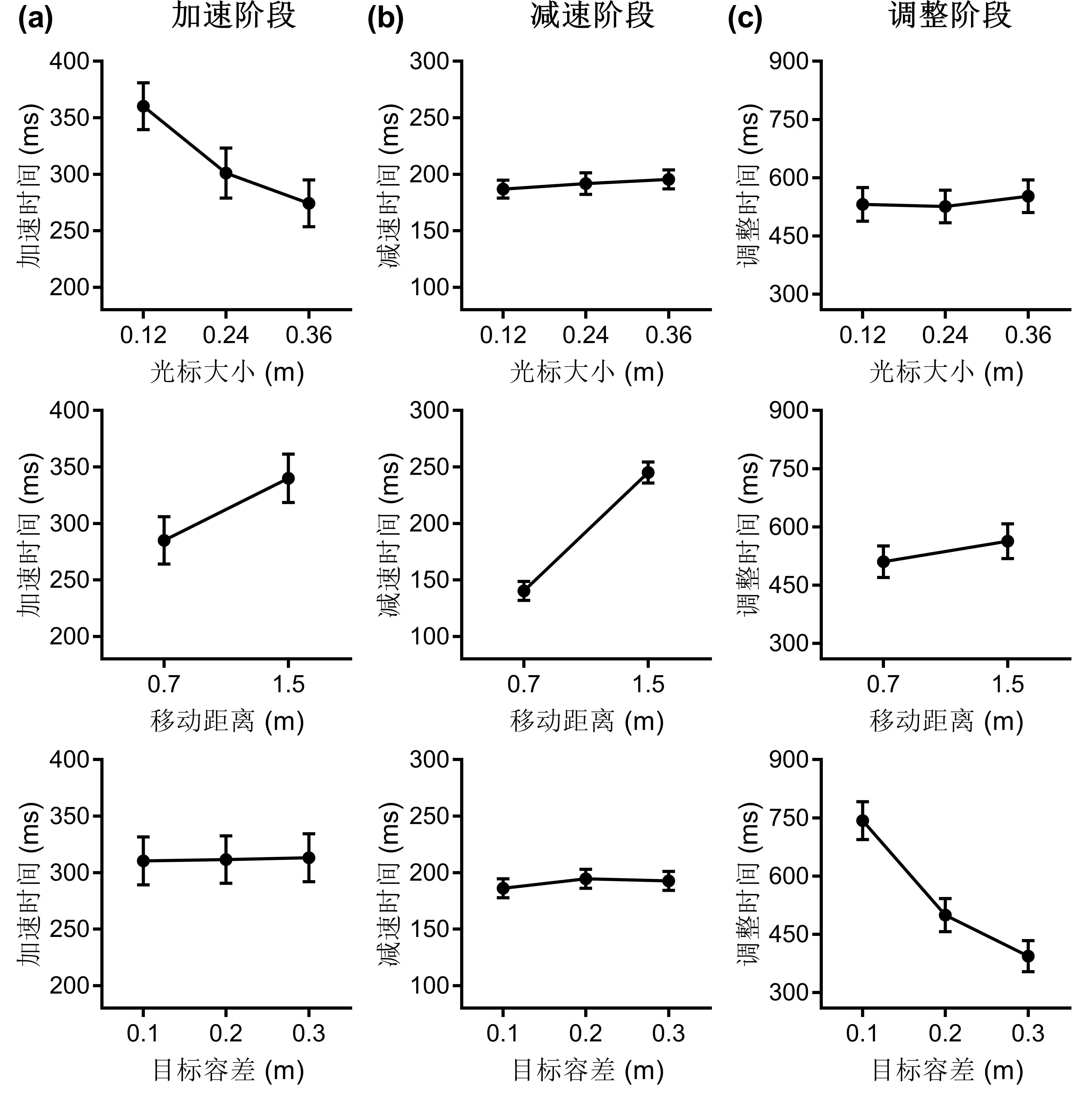
图4 实验1的加速阶段(a)、减速阶段(b)和调整阶段(c)的操作时间与光标大小、移动距离和目标容差的关系图

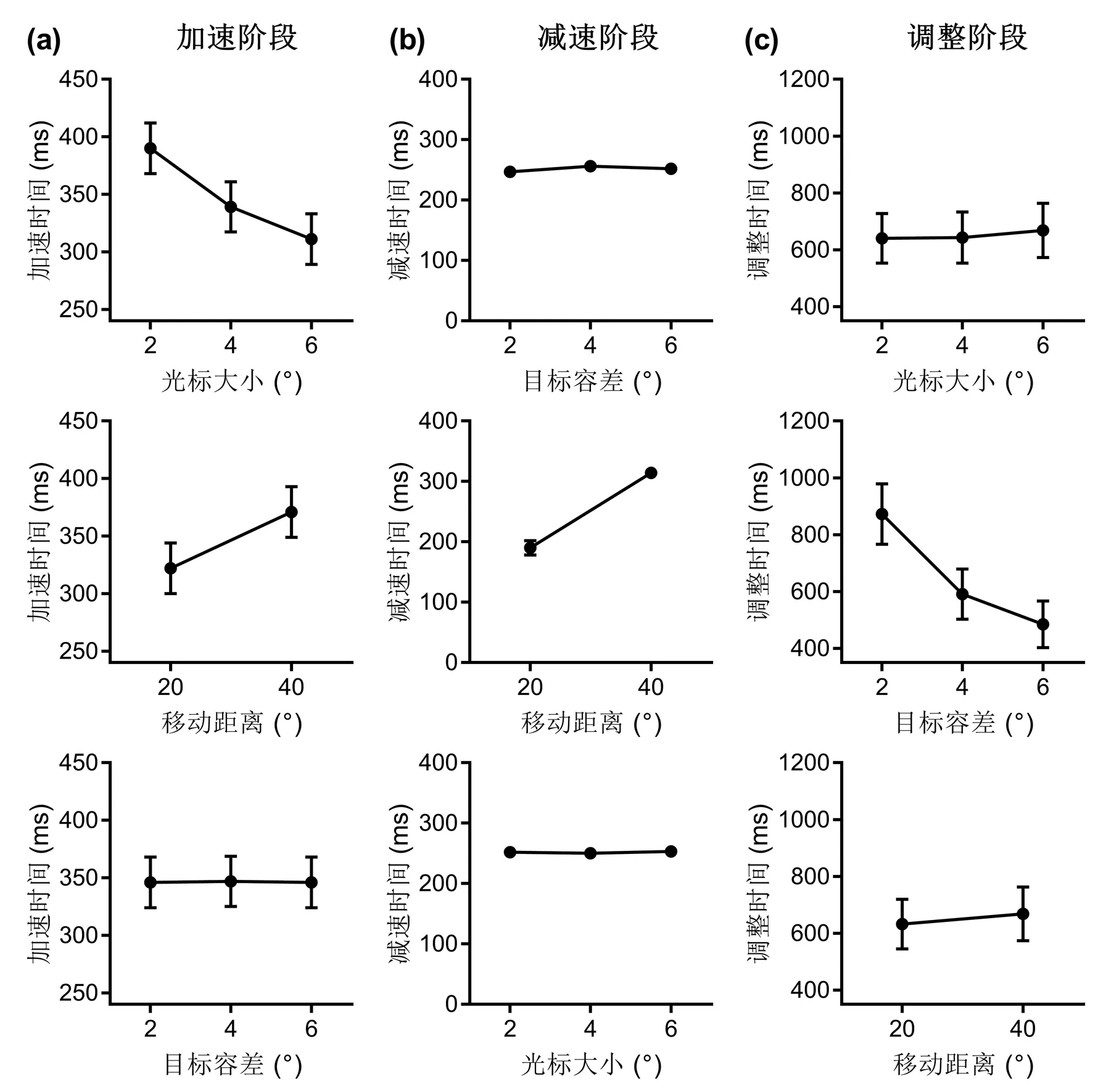
图5 实验2的加速阶段(a)、减速阶段(b)和调整阶段(c)的操作时间与光标大小、移动距离和目标容差的关系图

3.3 模型拟合

我们在前期的研究中提出了三阶段模型解释加速阶段、减速阶段和调整阶段的操作表现[13]，三阶段模型如下：加速阶段：MTA=a+b[log2(2A)+c/OS]

减速阶段：MTD=a+blog2(2A)

调整阶段：MTC=a+b[log2(2A)-clog2(TT)+d(OS-0.18)2]

图6 实验1和实验2的三阶段模型拟合结果。(a)实验1线性量数据拟合结果。(b)实验1角度量数据拟合结果。(c)实验2角度量数据拟合结果。 IDA=log2(2A)+c/OS；IDD=log2(2A)；IDC=log2(2A)-clog2(TT)+d(OS-0.18)2(a)或者IDC=log2(2A)-clog2(TT)+d(OS-4.96)2(b和c)。

MT表示操作时间，A表示移动距离，OS表示光标大小，TT表示目标容差，a、b、c和d是模型拟合常数。在本研究中，目标大小、移动距离和目标容差对操作表现的影响与我们前期的结果基本一致，因此我们验证三阶段模型是否适合角度量参数。在公式3中，光标直径0.18 m对应的平均角度为4.96°，由于实验1和实验2的光标大小参数恰好在0.18 m和4.96°的两侧，可能造成了统计结果的不显著，但是随着光标的增大，调整时间仍然表现出了轻微的先下降后上升的变化趋势，我们认为光标大小仍然是重要因素，并将公式3中的0.18 m替换成角度4.96°。公式3修改如下：

调整阶段：MTC=a+b[log2(2A)-clog2(TT)+d(OS-4.96)2]

我们使用三阶段模型(公式1，公式2和公式3)拟合实验1的线性数据，发现三阶段模型不能很好地解释减速阶段和调整阶段的数据变化(加速阶段：R2=0.931；减速阶段：R2=0.579；调整阶段：R2=0.843)。我们将实验1的线性参数转换成角度参数，发现三阶段模型(公式1，公式2和公式4)的拟合结果显著提高了，所有的相关系数超过了0.9(加速阶段：R2=0.921；减速阶段：R2=0.957；调整阶段：R2=0.969)。此外，三阶段模型也能很好地解释实验2的角度数据(加速阶段：R2=0.939；减速阶段：R2=0.974；调整阶段：R2=0.935)(图6)。结果说明我们提出的三阶段模型能够适用于角度参数。实验1和实验2的模型拟合结果详细参数见表1。

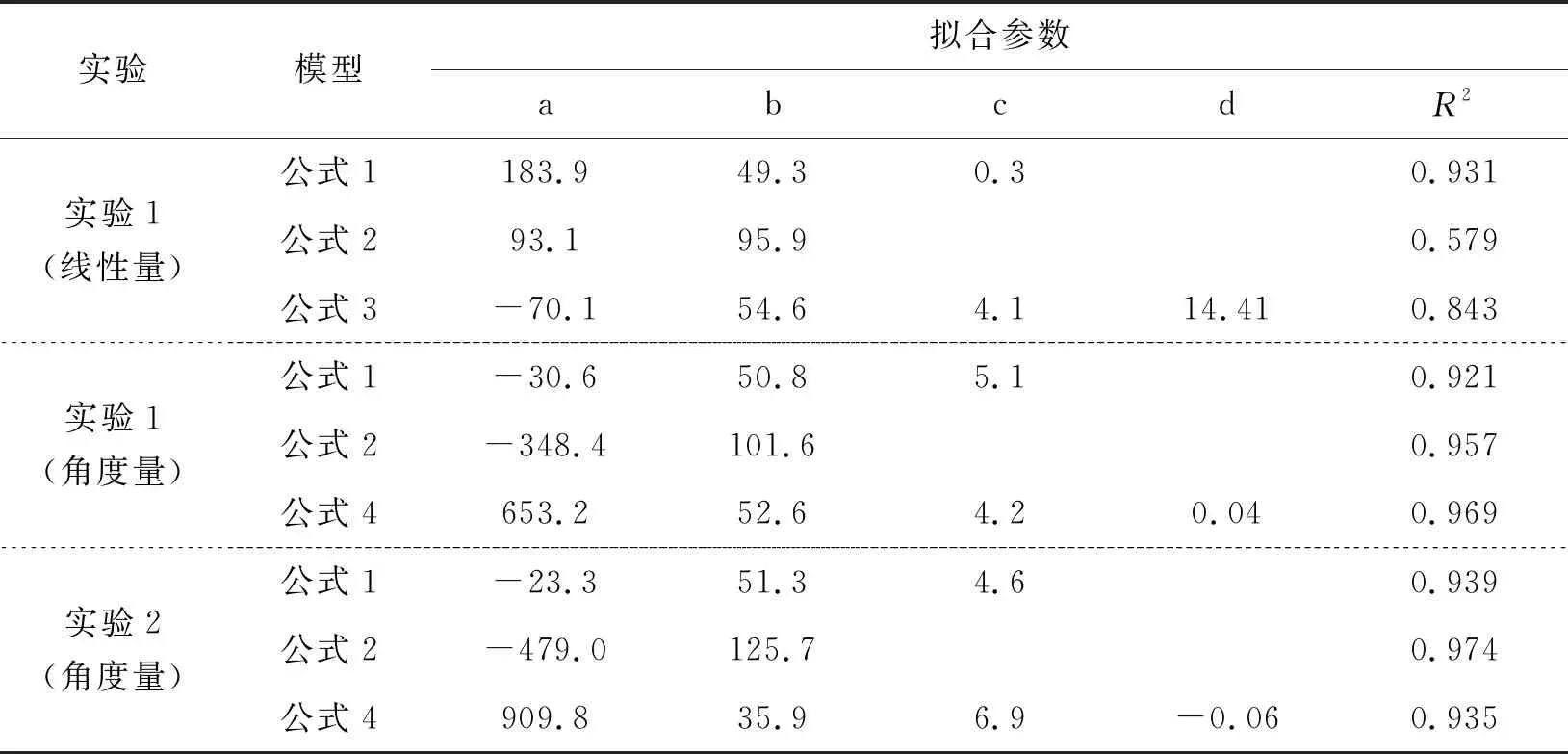
表1 实验1和实验2的三阶段模型拟合结果

4 讨论

本研究从移动过程详细分析了分别使用线性量和角度量表示参数的情况下深度对人类完成放置任务操作效率的影响。当使用线性量参数时，深度对减速阶段和调整阶段的操作时间造成了相反的影响，原因可能与VR中的远距离操作方式的特点有关。由于远距离移动操作主要依靠的是手臂的转动，因此操作表现受到转动角度大小的影响。由于减速阶段占据了约1/3的移动距离，并且随着深度的增加，减速阶段移动的距离占总移动距离的比例逐渐降低(深度=2 m：39.2 ±5.1%；深度=3 m：32.0±7.1%，深度=4 m：27.2±5.8%)，因此，相同的线性移动距离对应的角度逐渐减小，导致减速时间减少。在调整阶段，操作时间快速增加的原因可能存在两方面。一方面，调整阶段属于慢速阶段，发生在目标物附近，需要较高的操作精度。操作时由于手臂悬空缺乏支撑平台容易导致手的抖动[14]。随着深度的增加，虚拟射线长度增加，射线前端的抖动越大，稳定性降低。另外一方面，调整阶段的主要影响因素是目标容差[13]，相同的线性量目标容差的角度量会随着深度的增加而减小，从而导致调整时间增加。因此，当目标的深度改变时，只要移动距离或者目标对应的视角大小不变，则操作效率不会受到影响。实验2的结果显示，深度对减速阶段和调整阶段的操作时间没有影响，并且三阶段模型能够很好地拟合角度量数据，证明了角度量参数包含了深度对操作效率的全部影响。这些结果表明在三维空间中用角度量表示参数的大小比使用线性量更简洁。

本研究对三维空间的交互设计提供了重要的参考价值。第一，我们的结果支持了三维空间中更适合采用角度量参数。第二，移动过程的三阶段模型比总操作时间的单一模型更全面地解释了人类的操作特性，并保证了模型的统一性，为不同任务或者交互工具的对比提供了稳定的方法。

本研究只采用了手柄操作完成任务，在VR中还存在其他的重要交互方式，比如头控和眼控等[9,15]，将来的研究将验证本研究结果能否扩展到其他的交互方式。此外，除了放置任务，旋转和缩放等任务也是VR中的常见操作任务[16]，深度如何影响完成其他任务的操作表现还需要进一步探索。

5 结论

本研究详细探讨了深度对完成放置任务的操作效率的影响。我们的结果证明了角度量参数完全包含了深度对操作时间的影响，并验证了三阶段模型适用于角度量参数。本研究的发现对三维空间的交互设计和操作特性模型的统一提供给了重要的参考。

致谢

感谢耿鹏和田宸宇对本研究的数据采集和分析提供的帮助。