一种面向自动驾驶推理任务的工作流调度策略
2021-03-21林凯,卢宇,陈星,林兵
林 凯,卢 宇,陈 星,林 兵
1(福建师范大学 物理与能源学院,福州 350117) 2(福州大学 数学与计算机科学学院,福州 350116)
1 引 言
随着机动车保有量的增加,道路拥堵、交通安全、环境污染等问题日益突出.自动驾驶车辆的发展为这些问题提供了新的解决方案.高度自动化的车辆驾驶可以提高驾驶的便利性和舒适性,提高道路系统的整体交通效率和安全性,缓解交通拥堵,大大减少人为失误造成的事故.此外,它还可以减少汽车尾气排放对环境的污染,显著提高燃油效率.
当自动驾驶车辆行驶在道路上,传感系统会检测当前的交通状况,将路况信息传递到车辆的推理系统中,推理系统需要在短时间内处理这些信息.随后,车辆的传动系统就能做出诸如加速、转向等一系列响应动作[1].由于OBU的计算能力不足,在容错时间约束下,选择合理的调度平台,优化自动推理任务的完成时间是自动驾驶技术中重点关注的问题.
边缘计算为了将计算任务卸载到终端用户附近的边缘服务器,利用计算和存储资源位于终端设备和云数据中心之间的边缘设备.其目的是将计算任务卸载到终端用户附近的边缘服务器,并在数据源附近处理计算任务,从而缩短响应时间.边缘环境下推理任务的分解与调度能够很好地满足推理任务的低延迟处理要求,并产生良好的实时处理效果[2].
在自动驾驶推理任务的研究中,很少关注推理任务的调度问题,大部分研究集中自动驾驶过程中的交通状况识别和推理分析[3-5].自动驾驶的推理任务调度问题类似于协同设计的任务调度和工作流调度.因此,协同设计任务和工作流调度的研究方案可以应用于自动驾驶推理任务工作流调度中.由于推理任务通常调度在OBU上[6],这将导致推理任务调度的高延迟,无法满足推理任务的安全性和实时性要求.目前,启发式算法被广泛应用于解决协同设计任务和工作流调度问题,如蚁群算法、粒子群算法、遗传算法等[7-9],这些算法虽然能较好地解决工作流调度问题和协同设计任务,但收敛速度慢,容易陷入局部最优解,不能很好地满足推理任务的低延迟要求.近年来,强化学习被应用于解决协同设计任务和工作流的调度问题.该算法通过与不确定环境的交互作用来修正实际值与预测值之间的偏差,收敛速度较快.这些研究为自动驾驶推理任务工作流调度提供了一种新的解决方案[10-12].虽然推理任务的结构类似于协同设计任务和工作流,但是自动驾驶车辆生成的推理任务需要满足实时系统的低延迟要求.因此,有必要设计合适的调度策略和算法,以满足自主驾驶推理任务的要求.
基于以上研究现状,针对自动驾驶推理任务实时系统,根据车辆驾驶过程中推理任务和边缘环境的变化,本文首先设计出一种在边缘环境下的自动驾驶推理任务工作流调度策略,并充分利用边缘计算平台的计算能力对推理任务进行调度.其次,利用SA-QL算法来寻找自动驾驶推理任务工作流的低延时调度方案.最后,本文对SA-RL算法和PSO算法进行了性能比较.
本文的主要贡献如下:
1)设计了一种推理任务工作流调度策略,考虑在不同时间窗内边缘环境和实时推理任务的变化情况,在满足任务约束的条件下计算任务完成时间;
2)在边缘环境下进行自动驾驶推理任务工作流调度处理,在满足推理任务约束条件下,减少任务完成时间;
3)引入SA-QL,结合本文提出的推理任务工作流调度策略,优化自动驾驶实时推理任务工作流执行时间.
本文余下部分组织布局如下.第2部介绍目前相关研究工作;第3部分对自动驾驶推理任务工作流调度问题进行描述与分析,确定问题模型以及要求解的目标,并用实例分析推理任务调度过程;第4部分提出了基于强化学习算法的推理任务工作流调度策略,设计了推理任务工作流调度算法来计算推理任务完成时间,提出了适用于本文研究问题的SA-QL算法;第5部分进行实验结果的讨论与分析,对SA-RL算法及PSO算法进行性能差异的分析;最后一部分总结全文,并讨论本文未来的改进与展望.
2 研究现状
针对自动驾驶,当前的研究工作主要集中于自动驾驶推理任务路况信息的推理决策和识别.例如Teichmann等人[3]提出了一种联合分类、检测和语义分割的语义推理方法,虽然加快了推理速度,在数据集中表现非常出色,但是仍存在着计算瓶颈和能耗大的问题,这些研究中,对推理决策过程进行建模优化,在自动驾驶推理决策问题中取得了不错的效果,但未涉及推理任务调度问题的研究工作;Vacek等人[4]提出了一种基于案例推理的认知汽车情景解释方法,该方法依靠基于案例的推理来预测当前场景的演变并选择合适的行为,但是没有使用实际场景进行测试来显示这种方法的潜力,而且没有提出如何评估无案例知识下行为后果的方法;高振海等人[5],针对决策过程的因果关联问题,建立了车辆跟驰行为的马尔可夫决策过程模型,基于增强Q学习算法对该模型进行求解,验证了方法的可行性与有效性,提升了决策过程的因果关联性,改善了传统决策方法中既定的逻辑切换策略并规避了固有设计理念中多参数调校的难题,使自动驾驶过程中车辆动作的选择更贴合实际,但是回报函数的设计缺少舒适性等其他指标的考虑,没有验证算法的稳定性;王娟娟等人[6]基于可并行的有向无环图提出了一种自动驾驶硬实时推理任务调度机制,保证所有进入车载计算系统的推理任务都能在其截止期之前完成,有效提升自动驾驶时应急避险的安全性,但是研究中将推理任务调度至车载处理器进行处理,存在着处理设备计算能力不足,处理时延高的问题,不能很好的满足自动驾驶推理任务的实时性要求.
由于自动驾驶推理任务与协同设计任务及工作流结构相似,因此将协同设计任务与工作流调度问题的研究方法应用于自动驾驶推理任务的调度上具有可行性.在工作流调度问题的研究中,研究者主要采用仿生算法进行问题求解,例如Meena等人[7]提出了一种元启发式成本效用遗传算法,考虑了云的异构性、按需付费价格模型,以及虚拟机性能变化和启动时间等因素,在云环境中,满足最后期限的同时,最大限度地降低工作流的执行成本,虽然在执行时间与执行成本上取得了不错的效果,但是未考虑到虚拟机的关闭时间,以及虚拟机部署在不同数据中心之间的数据传输成本,这些因素将影响工作流的总体执行成本.Zhu等人[8]基于进化多目标优化算法来解决基础设施即服务平台上的工作流调度问题,提出了一种针对特定问题的编码和种群初始化、适应度评价和遗传算子的新方案,结果表明,算法具有较高的稳定性,可以获得更好的解决方案,但未考虑多个定价方案、实例类型、云的情况以及通信和存储的成本;Xie等人[9]提出了一种全新的非局部收敛粒子群优化算法,应用非线性惯性权重来平衡和调整粒子的全局和局部搜索能力,通过加速粒子群加快近最优解的搜索速度,通过选择和变异操作,使粒子群以一定的概率逃离局部极值,保持粒子群的多样性,减少极大地降低了云边缘环境下工作流调度的时间和经济成本.
随着强化学习算法的发展,一些研究者将其运用至协同设计任务及工作流调度问题中,并取得了不错的效果.例如,Wang 等人[10]将深度Q网络模型应用于多代理增强学习环境中,以指导云上多工作流的调度,构建了一个马尔可夫博弈模型,该模型以工作流应用程序和异构虚拟机的数量作为状态输入,以最大完成时间和成本作为回报,优化了多工作流的完成时间和用户成本,虽然生成调度策略优于传统算法,但是提出的方法未考虑更多的QoS指标,如可靠性、安全性、负载平衡等,并且依赖于任务和候选云服务器的QoS数据信息,在实际应用中,如果历史QoS数据不足,收集数据的工作十分昂贵和耗时;Orhean等人[11]针对分布式系统中的调度问题,考虑了节点的异质性及其在网格中的配置,提出了一种强化学习算法,从而确定一个更低执行时间的调度策略,但是由于分布式系统的复杂性,学习模型存在局限性,当系统添加的节点过多,强化学习代理将无法正确学习最佳策略.陈圣磊等人[12]建立了任务调度问题的目标模型,给出调度问题的马尔可夫决策过程描述,提出一种基于多步信息更新值函数的多步Q学习调度算法(Multi-step Q Learning Algorithm,MQ),该算法收敛速度较快,能有效地解决任务调度问题,虽然采用多步Q学习算法能有效平衡协同设计任务调度的计算量和预见能力,但是由于算法步数的变化对算法性能有较大影响,而在自动驾驶推理任务工作流调度问题中,路况复杂性大,实时推理任务各同,数量大,不可能对所有实时推理任务进行参数优化,所以MQ算法并不适用于本文所论述的问题.
目前对自动驾驶推理任务调度的研究相对不足,因此本文从协同设计任务与工作流调度研究方法出发,对边缘环境下的自动驾驶产生的实时推理任务调度问题进行研究讨论.一方面,本文设计了一种推理任务工作流调度策略,通过SA-QL优化推理任务工作流完成时间,在严格容忍时间限制满足推理任务实时系统低时延的约束条件,提高自动驾驶过程中推理任务调度的成功率;另一方面,本文证明了SA-RL算法和PSO算法在自动驾驶推理任务工作流调度问题上的可行性,并进一步分析了SA-RL算法和PSO算法在自动驾驶推理任务工作流调度问题求解中的性能差异.
3 问题描述
3.1 问题定义
对于自动驾驶推理任务而言,任务具有实时性的特点,在不同时间窗内会产生不同实时推理任务,并且边缘环境中边缘节点数量也在不断发生变化.图1描述了边缘环境下自动驾驶车辆产生的推理任务的不同以及边缘节点在不同时间窗中的变化情况.

图1 不同时间窗上边缘环境及推理任务变化情况Fig.1 Change of edge environment and reasoning task in different time windows



(1)
(2)
(3)
(4)
为了在边缘环境中更好地利用边缘节点的计算资源,规定边缘节点调度处理子任务要满足特定的处理原则:
1)在相同边缘节点上的子任务要按深度串行执行,若深度相等,则按子任务序号升序执行,子任务深度由公式(5)表示;
2)在不同边缘节点上的子任务可并行执行;
3)每个子任务只能被一个边缘节点所调度,由公式(6)表示;
4)当边缘节点上分配的所有子任务传输完成时开始处理子任务.
(5)
(6)

(7)
(8)
根据以上定义,自动驾驶推理任务工作流调度问题可以形式化地描述为:合理指派子任务到各个边缘节点上处理,结合推理任务工作流调度策略,在满足实时推理任务可容忍时间、子任务间偏序约束以及边缘节点处理原则下,优化实时推理任务完成时间,如公式(9)所示:
(9)
formula(6)
3.2 问题分析
图2为某个时间窗下边缘环境及自动驾驶车辆推理任务情况,此时边缘环境中有2个边缘节点{f1,f2},自动驾驶汽车产生的实时推理任务可划分为4个子任务{n1,n2,n3,n4},子任务间有着4条时序约束有向边{e1,2,e1,3,e2,4,e3,4},可容忍时间为30毫秒.

图2 边缘环境及自动驾驶车辆推理任务情况Fig.2 Edge environment and reasoning task of autonomous vehicle
该实时推理任务存在可行调度方案,其边缘节点-子任务匹配矩阵如表1所示,表2为边缘节点-子任务平均传输时间矩阵,表3为边缘节点-子任务平均完成时间矩阵,表4为子任务-子任务平均传输时间矩阵,实时推理任务调度过程如3所示,总完成时间为17毫秒,其中所有子任务传输至边缘节点的传输时间为3毫秒,调度时间为14毫秒,最差调度下调度总时间为24毫秒,小于实时推理任务可容忍时间.

表1 边缘节点-子任务匹配矩阵Table 1 Matching matrix between edge-node and sub-task

表2 边缘节点-子任务平均传输时间矩阵Table 2 Average transmission time matrix between edge-node and sub-task

表3 边缘节点-子任务平均完成时间矩阵Table 3 Average completion time matrix between edge-node and sub-task
图
表4 子任务-子任务平均传输时间矩阵Table 4 Average transmission time matrix among sub-tasks

图3 实时推理任务调度过程Fig.3 Scheduling process of real time reasoning task
4 基于强化学习算法的推理任务工作流调度策略
在自动驾驶汽车运行过程中,路况不断发生变化,感知系统不断将路况信息传递给推理系统,推理系统处理的实时推理任务在不断变化,而这些实时推理任务往往有着不同的约束条件,为了在满足约束条件的前提下,降低调度处理时延,提出一种推理任务工作流调度策略,在该策略下,假设自动驾驶车辆所处的边缘环境为理想状态,即在当前时间窗内边缘环境中所有边缘节点都没有宕机的情况,其中推理任务工作流调度算法根据当前时间窗的边缘环境及实时推理任务来计算完成时间.
4.1 推理任务工作流调度策略
在不同时间窗内,自动驾驶车辆产生的实时推理任务与边缘环境将动态发生变化,有以下变化情况:
1)实时推理任务分解后的子任务数量;
2)实时推理任务分解后的子任务间偏序关系;
3)实时推理任务的可容忍时间;
4)当前时间窗可用边缘节点数.
实时推理任务完成时间与自动驾驶车辆产生的实时推理任务与边缘环境的变化有关,因此推理任务的完成时间就要在动态变化的边缘环境中进行计算.
推理任务工作流调度算法如算法1所示.
算法1.推理任务工作流调度算法
输入:si,mi,Gi,Ami×si,Cmi×si

1.初始化:入度数组I→∅及节点队列Q→∅,直接前驱节点集合R→∅,前驱任务数据最长传输时间T(i)→0
2.由Gi计算I(i)
3.将I(i)=0的节点入队,设置当前深度p→1,已遍历的节点数u→0,当前层的节点数k为当前队列大小
4.whileQ≠∅
5.ifu=kthen
6.p→p+1,u→0,k为当前队列大小
7.end if
8. 队首出队,出队节点为v,设置D(v)→p
9.u→u+1
10.fori←0tosi
11.if存在v至i的有向边then
12. 将v加入R(i)
13.I(i)→I(i)-1
14.T(i)→MAX(T(i),V(v,i))
15.ifI(i)=0then
16. 将任务i加入Q
17.end if
18.end if
19.end for
20.end while
21.由Ami×si为边缘节点分配子任务
22.同一边缘节点中子任务按任务深度值升序排序
23.初始化:完成列表O→∅,子任务剩余执行时间Y(i)=C(*,i)+T(i),当前时间h→0
24.whileO中元素个数小于si
25. 为每个边缘节点确定要执行的子任务,该子任务要满足其直接前驱集合为O子集
26. 在当前执行的子任务中找出最少执行时间w
27.Y(i)→Y(i)-w,如果Y(i)=0,则加入O
28.h→h+w
29.end while
30.returnh
4.2 强化学习算法
4.2.1 马尔可夫决策过程模型
马尔可夫决策过程(Markov Decision Process,MDP)模型是强化学习算法的基本模型,由于现实环境中状态转移的概率往往和历史状态有关,这样很难建立模型,因此可以根据马尔科夫性(即无后效性,也就是指环境中的下个状态只与当前状态信息有关,而与历史的状态无关)来简化模型,使得下个状态只与当前状态和所采取的动作有关[13].
本文所研究的任务调度问题有以下特点:
1)没有任何的先验模型;
2)状态空间中可解状态数随子任务数以及可行解约束条件动态变化;
3)动作空间中的动作数与子任务数相等.
既要满足子任务时序约束,又要满足严格容忍时间约束
基于以上特点,本文的MDP模型如下:
·智能体:子任务
·状态:边缘节点-子任务分配矩阵
·动作:动作空间内动作数等于子任务数si,如果当前状态au,k=1表示第k个子任务当前部署在第u个边缘节点中,那么执行动作k后,au,k=0,ax,k=1,其中x=(u+1)%mi表示将第k个子任务部署到下一个边缘节点
4.2.2 基于推理任务工作流调度策略的Q-learning算法
Q-learning是一种时序差分(Temporal-Difference,TD)算法,它基于随机过程且不依赖模型(Model-Free),无状态转化概率矩阵.由于算法更新价值函数时会选择最大价值进行更新,而动作选择不一定按最大价值所对应动作,因此会导致价值函数的乐观估计,由于这一特性,Q-learning属于离线策略(off-policy)学习方法[14].
Q-learning价值函数根据
Q-learning价值函数更新方式如下:
Q(s,a)=Q(s,a)+α[r+γmaxa′Q(s′,a′)-Q(s,a)]
(10)
其中α为学习效率,表示价值函数更新的程度,r为即时奖励,表示转移至下一个状态所得到的奖励,γ为折扣因子,表示后续状态的价值对当前状态的影响程度,maxa′Q(s′,a′)为选取的价值最大的状态-动作对的值.
由于:
Qreal=r+γmaxa′Q(s′,a′)
(11)
Qeval=Q(s,a)
(12)
因此,价值函数更新公式可进一步表示为:
Q(s,a)=Q(s,a)+α(Qreal-Qeval)
(13)
即Q-learning价值函数的更新可表示为价值函数值加上现实值与估计值的差值与学习效率的乘积.
为了平衡算法的探索与开发,本文采用Metropolis准则[15]进行动作的选择,其中退火策略采用等比降温策略:
Tk=θkT0
(14)
其中T0为初始温度,k为当前回合次数,θ为降温系数.
为减小状态-动作值表大小,减少状态搜索耗时,本文选择在可解状态空间中进行探索,即算法中探索的所有状态均满足公式(9)中的约束条件.基于推理任务工作流调度策略的Q-learning算法如算法2所示.
算法2.基于推理任务工作流调度策略的Q-learning算法
输入:回合数,回合迭代数,初始状态,初始温度
输出:Q(s,a)
1.fori←0to回合数
2. 随机选取动作,使初始状态变为可行解
3.forj←0to回合迭代数
4. 根据Metropolis准则选择动作,该动作转移的状态必须为可行解状态
5. 执行动作,转移状态
7. 根据<当前状态,选择动作,即时奖励,转移后状态>四元组信息由公式(10)进行价值函数的更新
8. 根据公式(14)进行对当前温度进行降温处理
9.end for
10.end for
5 算法实验与分析
5.1 实验参数设置
通过多次实验调参结果,本文设置强化学习算法参数:α=0.01,γ=0.9,λ=0.5,λ为Sarsa(λ)[16]、Q(λ)[16]算法中效用迹矩阵衰减率,回合数为100,回合迭代数为1000;设置PSO算法参数:ω=0.9,c1=2,c2=2;设置模拟退火参数:T0=150,θ=0.9.
本文采用文献[12]的调度实例,假设该实时推理任务可容忍时间为 60毫秒,任务分解后有7个子任务,子任务间时序约束的DAG如图4所示.

图4 子任务间时序约束的DAGFig.4 DAG with temporal constraints among sub-tasks
设当前边缘环境中有3个可用边缘节点,子任务在各边缘节点上平均完成时间、平均传输时间、子任务间平均传输时间如表5、表6、表7所示.

表5 边缘节点-子任务平均传输时间矩阵Table 5 Average transmission time matrix between edge-node and sub-task

表6 边缘节点-子任务平均完成时间矩阵Table 6 Average completion time matrix between edge-node and sub-task

表7 子任务-子任务平均传输时间矩阵Table 7 Average transmission time matrix among sub-tasks
5.2 对比算法
为了验证SA-RL算法在自动驾驶推理任务调度上的有效性,本文选择TD(0)算法:Sarsa[17],TD(λ)算法:Sarsa(λ)、Q(λ)作为对比算法.为了比较SA-RL与传统启发式算法的性能区别,本文选择PSO[18]作为比较算法,其中PSO算法中粒子比较方式[19]如下:
1)两个粒子都满足可行解条件:选择完成时间较小的粒子;
2)两个粒子都不满足可行解条件:选择完成时间较小的粒子;
3)一个粒子满足可行解条件,一个粒子不满足可行解条件:选择满足可行解条件的粒子.
5.3 实验结果与分析
本实验的实验环境为,CPU:Intel(R)Core(TM)i7-4720HQ CPU 2.60GHz,内存:8GB,操作系统:Windows 10,编程语言:Python.
由搜索算法可得状态空间可解状态数为2042个.
在该实例中,SA-RL算法和PSO算法均能找到2个最优边缘节点-子任务匹配矩阵:

传输时间为3毫秒,实时推理任务最短的最佳运行时间均为32毫秒,匹配矩阵1对应分配策略的调度处理过程如图5所示.

图5 最优分配策略1调度处理过程Fig.5 Scheduling process of optimal allocation strategy 1
以图5为例分析对应边缘节点-子任务分配方案调度过程:
1)根据子任务深度与子任务序号为边缘节点分配子任务:f1:{n1,n4,n5},f2:{n2,n7},f3:{n3,n6};
2)经过3毫秒,所有子任务卸载到对应的边缘节点上,子任务1卸载至边缘节点1上执行,到6毫秒时子任务1完成;
3)子任务2经过卸载至边缘节点2上,经过2毫秒任务间的数据传输时间,子任务开始执行,到10毫秒时,子任务2完成;
4)子任务3、4分别卸载至边缘节点3、1上,经过1毫秒任务间的数据传输时间以及4毫秒的任务处理时间,到15毫秒时子任务4完成,此时子任务3还剩2毫秒的数据传输时间以及2毫秒的任务处理时间;
5)子任务5卸载至边缘节点1进行任务调度,到19毫秒时,子任务3完成,此时子任务5还剩2毫秒的数据传输时间以及2毫秒的任务处理时间;
6)子任务6卸载至边缘节点3进行任务调度,到23毫秒时,子任务5完成,此时子任务6还剩1毫秒的任务处理时间;
7)经过1毫秒,到24毫秒时,子任务6完成;
8)子任务7卸载至边缘节点2进行任务调度,经过5毫秒任务间的数据传输时间以及3毫秒的任务处理时间,到32毫秒时完成调度.
SA-RL算法与PSO算法每10回合平均完成时间如图6所示.随着回合数不断增加,各算法平均完成时间不断降低,平均完成时间均低于可容忍时间.从图中可以看出,回合刚开始,强化学习算法平均完成时间波动较小且维持在较高水平,这是因为初始温度较高,因此选择随机动作的概率较大;但是随着Metropolis准则的降温处理,回合即将达到设定的回合数时,强化学习算法以接近于1的概率选择最佳动作,因此算法平均完成时间不断下降,其中Sarsa(λ)、Q(λ)算法收敛较早,这是因为算法中引入了效用迹矩阵,采用多步更新策略,因此能加快收敛速度.

图6 每10回合平均完成时间Fig.6 Average completion time of every 10 rounds
除此之外,PSO算法的平均完成时间虽然一直在下降但是波动较大,平均完成时间会维持在较高水平,这是由于启发式算法收敛速度慢、易陷入局部最优解的特点导致的.
SA-RL算法每10回合平均奖励如图7所示.随着回合数不断增加,各强化学习算法平均奖励不断提高,在后期收敛过程中Sarsa(λ)、Q(λ)的平均奖励值维持在较高水平,这是由于算法收敛速度快,因此会更快得到更优的价值函数.

图7 每10回合平均奖励Fig.7 Average reward of every 10 rounds
SA-RL算法与PSO算法每10回合完成时间平均方差如图8所示.从图中可以看出PSO算法与SA-RL算法相比,平均方差维持在较高水平,平均完成时间波动较大.Sarsa(λ)、Q(λ)较其他强化学习算法而言,收敛较快,平均方差能维持在较低水平,平均完成时间波动较小.
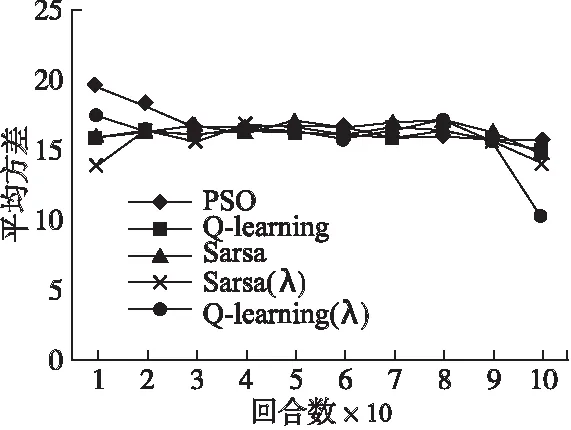
图8 每10回合完成时间平均方差Fig.8 Average variance of completion time
SA-RL算法运行5次探索到所有可解状态数时的回合次数如表8所示.从表中可以看出SA-RL算法探索到所有可解状态数的回合数相差不大,其中TD(λ)算法探索到所有可解状态所需的回合次数少于TD(0).

表8 探索到所有可解状态时的回合次数Table 8 Amount of rounds when SA-RL found all feasible states
SA-RL算法运行5次探索到所有可解状态数时的耗时如表9所示.从表中可以看出当探索到所有可解状态时,Q-learning、Sarsa较Sarsa(λ)、Q(λ)而言耗时较短,原因是Sarsa(λ)、Q(λ)算法进行学习时不仅要对遍历过状态的状态-动作表进行更新,还要对效用迹矩阵进行更新,随着状态空间的增大,算法所要更新的表空间不断增加,因此耗时较长.

表9 探索到所有可解状态时的耗时Table 9 Time when SA-RL found all feasible states
综上所述,对于自动驾驶实时推理任务工作流调度问题,SA-RL算法与PSO算法在实验中均能找到符合约束条件的优解,均具备可行性的特点;强化学习算法与PSO算法每回合平均完成时间均随着回合数增加不断降低,不断趋于收敛状态,证明了强化学习算法与PSO算法的有效性;在探索可行解状态过程中,Q-learning、Sarsa耗时较短,表明TD(0)算法探索性较强;由每回合平均完成时间与完成时间平均方差的变化,可以看出Sarsa(λ)、Q(λ)收敛较快,平均方差最终维持在较低水平,波动较小,表明TD(λ)算法的收敛性更强.
6 结 论
针对自动驾驶推理任务工作流调度问题,提出了一种基于强化学习算法的推理任务工作流调度策略.实验结果表明,该策略能快速有效地找到满足容错时间的调度方案.SA-QL和Sarsa在探索可行状态上所耗费的时间更少.这说明TD(0)算法更具探索性.从平均完成时间的变化以及平均方差可以看出,Sarsa(λ)和Q(λ)收敛更快.此外,Sarsa(λ)和Q(λ)的平均方差保持在较低水平,波动较小.实验表明,TD(λ)算法具有良好的收敛性.
在未来的工作中,我们将考虑云计算和车联网混合环境下的调度问题,以促进卸载设备的多样性和任务调度的灵活性.此外,我们还将考虑使用RL算法结合深度学习技术来优化推理任务的完成时间.
