提升小学生运算能力的实践探索
2021-03-21陈晶
陈晶

[摘 要] 我国学生的计算能力一直都被全世界认可,但教师过多地把关注的焦点放在计算是否正确与方法和技巧是否熟练上,也被人们所诟病。我们要追求的是具有核心素养(理解算理、含有数学思想)的运算能力。因此,提升学生的运算能力,必须发展学生的思维能力。
[关键词] 小学数学;运算能力;数学基本思想
数学是研究数量关系的一门学科,“数与代数”领域占小学数学课程的比例较高。长期以来,“计算又对又快”是评价学生运算能力的重要指标。因此目前不少运算教学还停留在“基本技能”层面,一味地追求效率、正确率。特别是在部分教师的观念中,认为计算教学最简单,学生做着做着就会了,算着算着就对了;教师不必大费周折,简单演示一遍计算过程,然后学生鹦鹉学舌地练习,学生就能熟练掌握计算方法。然而反复、机械的训练容易产生负面影响。例如,“25×4÷25×4=1”是小学生普遍存在的运算错误。因为学生过度接受训练,一看到25和4就产生了条件反射,脑海马上浮现了100。接受式学习、机械式练习的课堂模式,无法培养出创新型人才。
《义务教育数学课程标准(2011年版)》的核心词中,运算能力是指能够根据法则和运算律正确地进行运算的能力,培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题。运算能力不是简单的加、减、乘、除的计算,而是观察能力、理解能力、推理能力、表达能力等综合能力。例如,计算0.7×72+5.6,有个别学生是这样计算的:0.7×8×9+5.6=5.6×9+5.6=5.6×10=56。若不具备很好的运算能力,则无法敏锐地观察和灵活地解决。因此,运算教学要从简单的计算技能练习转向学生运算能力的提升和学生思维品质的提高。
一、借助几何直观理解算理,提升运算能力
华罗庚曾说过:“数缺形时少直观,形少数时难入微。”借助几何直觀让学生对运算本质的认识与理解不再停留在感性认识阶段,而是创新思维和高阶思维的结果,更是理性认识的升华。
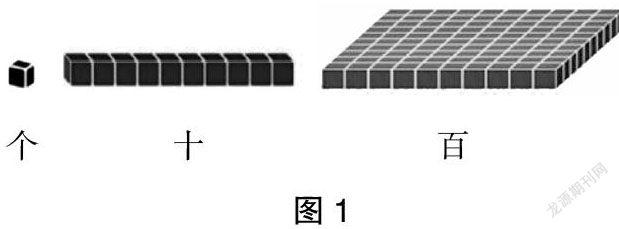
在以往计算教学过程中,教师的教学重心往往落在学生会算上(算得又对又快),即更关注学生对算法的掌握(这是程序性思维),而忽略了学生对算理的理解。以人教版三年级上册第四单元“万以内的加法”为例,部分教师特别重视学生对算法的总结,让学生回顾“271+31”是怎样计算的,即使学生总结算法时指着算式“271+31”说“末位对齐”,老师还是不厌其烦地纠正:“不是末位对齐,是相同数位对齐。”在教学时,我们是否可以不要过多地在意学生算法概括的标准化,而是应该探究算法背后的算理呢?此时与其咬文嚼字地表述算法,不如直达数学本质地追问:“为什么要对齐?”教师可以出示各级计数单位的立方体模型(如图1所示),学生直观地观察一层对应的计数单位“百”,一行对应的计数单位“十”。如果是首位对齐,那么就是2层立方体模型加上3行立方体模型得到“5”,这个“5”既不表示5层,也不表示5行。以此类推,7行立方体模型加上1个立方体模型,结果“8”既不表示8行,也不表示8个。如果是相同计数单位对齐再相加,那么3行加7行得到10行,10行满一层应该向前进一位;1个加1个得到2个。它们表示的都是相同计数单位的累加。通过几何直观可以把复杂、枯燥的算法文字变得简明、形象,有助于学生深刻地理解算理。从起步的会算和知道,走向深层意义和内在本质的理解。史宁中教授曾说:“数学教育的根本是培养学生的数学直观。”依赖几何直观可以让学生“看”出运算中蕴藏的算理,并正确地进行运算。
分数是公认的小学阶段学生学习的难点,分数的四则运算借助几何直观能让学生更好地理解蕴藏在算法背后的算理。笔者在教学“分数乘法”时,有学生提出:“为什么分数乘法要分母相乘作分数分母,分子相乘作分数分子?”还有学生通过画简单的长方形图(如图2所示)解释×的算法,其他学生观察图形后得到启发:“分数乘法因为是分了又分,一共分了5×2=10(份),所以是分母乘分母;因为是取了又取,一共取了4×1=4(份),所以是分子乘分子。”学生运用数形结合思想,借助直观图形解释分数乘法的算理,提高了课堂教学效率,提升了运算能力。
二、设计挑战性问题,提升运算能力
史宁中教授提出:“为了培养学生的思维能力,为了发展学生的核心素养,应当设计一个开放的、有挑战性的问题。”在运算教学中,设计有挑战性和多元化的问题容易激发学生的探究兴趣,让枯燥的计算变成有意义的探究,从而提升学生的运算能力。例如,教学“整数乘法运算定律推广到小数”,笔者在课堂“巩固练习”设计了这样一道开放性的挑战题:“请补充算式5.3×0.25_________,并计算,使算式可以简便计算。”该道题是乘法运算定律的逆向变式,改变了传统单一的解答,答案是不确定的、多元的。该道题不能简单地应用某个乘法运算定律解决,真正做到让学生一题多练,体现解决问题策略的多样化。学生深刻理解乘法运算定律后,能综合运用所学知识和技能,寻求合理、简洁的运算途径解决问题。课堂上先让学生观察算式中数的特点,然后让学生独立思考、小组交流后创造出多种解题方法。方法一,乘法结合律:5.3×(0.25×4);方法二,乘法分配律:①5.3×0.25+0.25×4.7;②5.3×0.25-0.25×1.3;③5.3×0.25+5.3×0.75。学生能分析算式中数的特点,从整体考虑各个运算定律之间的联系与区别,从而培养学生解决问题的能力、应用意识和创新意识。学生的整个学习过程告别了“记忆、理解、应用”的低阶认知思维的过程,达到了《布鲁姆教育目标分类法》中的“分析、评价、创造”的高阶认知思维的过程。课堂上的挑战性、开放性问题,能够打开学生的思维空间,发散学生的思维,让学生对运算的理解更加透彻,从而提升学生的运算能力。
三、渗透数学思想,提升运算能力
史宁中教授指出:“数学基本思想归结为三个核心要素,即‘抽象、推理、模型’。”人民教育出版社小学数学编辑社王永春主任认为:“抽象、推理、模型中最重要的是逻辑推理,这是数学本质里最核心的部分。”数学运算的算理与算法的本质都是逻辑推理。
教师在运算教学中应渗透归纳推理,例如,“两位数乘两位数的笔算乘法”是在口算乘法、多位数乘一位数的笔算乘法的基础上,先通过学习12×20、14×12、48×37等几个有限例子再探索计算的方法,接着让学生小组交流,然后总结出算法。学生经历这个过程得到运算法则,其实就运用了归纳推理。小学数学教学中发现规律(如分数的基本性质、积的变化规律),通常是先出示一些例子,然后观察、猜测、验证(举更多的例子),这其中也运用到了归纳推理。笔者在教学生如何发现规律时,尝试让学生先观察“13+31=44,29+92=121,54+45=99”这组算式,然后小组交流、讨论:“你有什么发现?”全班开始汇报发现的算式规律:“加数都是两位数,两个加数个位与十位交换位置,加数的数字不变。”还有学生补充道:“它们的和都是11的倍数。”此时引导学生大胆猜想并归纳结论:“将一个两位数的个位数与十位数交换后得到一个新数,它与原数相加,和是11的倍数。”之后让学生自己尝试举几个不同的例子,验证结论是否正确:56+65=121(11的11倍),23+32=55(11的5倍)……同样在发现算式规律的教学中,也渗透了归纳推理。在学生学习了整数运算定律后,教学小数、分数的运算定律时,通过与整数的运算定律类比得到整数运算定律在小数、分数中同样适用。学生通过大胆猜想、举例、观察、验证,最后得到结论。此时在运算教学中就渗透了类比推理的数学思想,提高了学生的运算能力。张景中院士曾说:“计算是具体的推理,推理是抽象的计算。”推理是重要的思想和方法,是数学基本的思维方式。无论是找规律、理解算理、总结法则等,都运用着推理的基本思想,从而促进学生运算能力的提升。
运算不单是一种技能,而且是一种基本的数学方法和数学意识。因此,在数学学习中,通过数的运算能促进、加深对所学数学知识的理解,发展数感,提升学生的思维品质。
3358501908297
