运用融合策略,培养学生学科核心素养
2021-03-21叶茂兰
叶茂兰
[摘 要] 核心素养背景下,关注运用融合策略,引导学生数学问题解决的过程。在教学与生活、教学与解决问题、教学与实操的融合过程中,在动态的教与学互动的过程中,学生将形成独立的品格,并提高关键能力。
[关鍵词] 学科核心素养;创新意识;解决问题策略;融合;推理能力;应用意识
核心素养指学生应具备的适应自身发展和社会发展需要的必备品格和关键能力[1]。学生核心素养的发展,是“立德树人”的根本保障。“学科核心素养=学科+核心素养”[2]。新课标要求:数学教学应当注重学生的符号意识、推理能力等的发展;特别指出的是适应新时代人才培养的需求,应注重学生应用意识与创新能力的发展。学生学科能力的发展体现了学科素养的发展,最终学生将形成独立的品格和关键能力的提高。
在教学实践中,学生的核心素养的培养,其实是在传统教学策略的基础上进行的,并不是独立于传统课堂教学以外的教学行为,这样学生的核心素养才能够在不断积累的过程中形成个人的品格和能力。同时,在校学习期间,学生思想意识的成长经历,知识与能力等的收获,将成为自身习得与不断成熟的基础,形成具有独立品质的人格。新时代背景下的数学课堂教学,遵循传统的教学模式,学生在教师的引导下采用一定的教学策略探究问题,教师和学生在动态交互探讨的过程中发现问题,提出疑惑,然后教师运用一定的教学策略在师生交互探讨问题过程中为学生解惑。因此,在实践中运用融合的教学策略能提升学生在课堂学习及实际生活中解决问题的技能,帮助学生在知识应用过程中掌握知识、发展素养。
一、融合生活策略,培养应用意识
学科教学要进入学生的生活和行为[3],即学科教学在社会生活背景中,融入培养学生学科素养的生活情境。走进生活,以具体的社会背景为题材,在立体的情境中以点带面,指导学生在实践中以讨论答辩或合作交流等形式解决问题。促进学生在言语交流与思考讨论的碰撞中开阔视野,促进学生应用意识的培养。
现代经济发展日新月异,数学与生活实践的互为应用十分明显,学生在实际情境中常会遇到诸多的生活问题,需要不断去解决。如果学生能有意识地应用数学知识去解决,那么学生的应用意识将变成潜在的品质。如针对教学生活中的百分数——利率,教师出示题目:“李妈有10万元钱,目前理财方式有三种:一是整存整取存款3年期(年利率2.7%);二是购买国债3年期(年利率3.8%);三是买银行理财产品一年一存(年利率4%),每年到期后,连本带息续买下一年的。3年后哪种理财方式收益更大?如果是你,你会选择哪种投资理财方式?”运用百分数计算利率的方法,学生计算得出第三种理财方式的利息最高、收益最大。但有学生提出了不同的理财观点,他认为购买理财产品利息虽高,但不足的是要3年后才能取回本金;3年整存整取利息虽最少,但优点是可以随时支取,资金提取方便,也是不错的理财方式。由此,其他学生也开始纷纷发表自己的见解,举出了很多生活中资金投资产生效益的事例。最后学生得出:李妈的10万元钱用第三种理财方式利息虽高,但如果进行其他正确的投资,融入社会经济生活中再利用,有可能带来更大的收益。这样把知识融入社会生活情境中,以事实说话最有感染力。
我们常说,实践是检验真理的唯一标准。数学知识的掌握,如果没有经过再运用,不一定能够积累经验。需要在一定的生活经历中加以应用、思考并得到验证以后,才能成为个人的能力。学生在后继的社会经历中,遇到类似的情境问题便会不自觉地加以应用,由此在这个过程中收获成功的喜悦。融合生活情境,学生在知识的认知与应用并举中获取知识、提升能力。数学的应用意识在社会生活情境中得到培养,把数学知识的教育向人的能力和行为的教育转变,实现数学学科素养的培养与提升。
二、融合动态实操策略,践行创新意识
新课标指出:教学中让学生在活动中自主探索,动手实践,经历实际操作,是重要的学习方式。有些抽象的数学问题,学生单纯依靠原有的知识无法直接获得。在不能提供有关信息和未启发的情况下,学生常常不知道如何下手。这时,通过教师提供的必要的媒介,如相应的图形或者实物,学生通过实际操作,就相当于为学生搭建了一个认知的支架,为学生在原有知识的基础上搭建了认知的抓手,学生就可以尝试去构建新的知识。学生亲历实际操作,从中“度”数学问题,在观察与思考中“悟”数学问题。
例如,教学“三角形的内角和”一课,先请学生动手“量一量”三角形的三个内角各是多少度,然后求和。有的学生得出的三个内角的和是180°,有的学生量出的结果是179°或者181°等。教材所呈现的求内角和的另一种方法是“动手‘折’角”。有的学生能顺利折出一个平角,有的学生折出来的三个角之间有空隙或者重叠等现象。在“先‘撕’角,再‘拼’角”的方法中,学生得出的结论比较统一,一致认为三角形的三个内角和是180°。是不是所有的三角形的内角和都是180°呢?可设计如下实际动手操作活动:
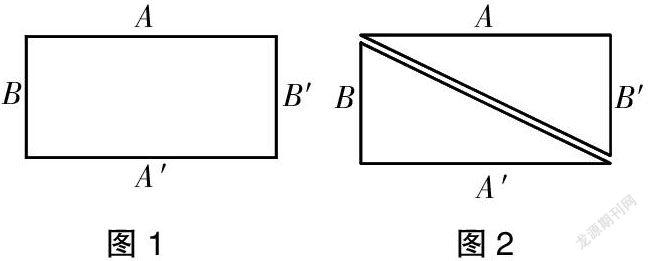
请学生打开学具袋,取出其中的长方形(每个小组的长方形的大小、形状有别)。两条长边分别标为A、A′,短边分别标为B、B′,而后要求学生计算这个长方形的内角和。学生得出长方形四个内角的和为4×90°=360°。然后,请学生在长方形内画一条线,把长方形分成两个完全相同的三角形,算一算每个三角形的内角和是多少度。学生得出每个三角形的内角和是360°÷2=180°。再让学生沿着刚才画的线,把长方形剪成两个直角三角形,如图2所示。
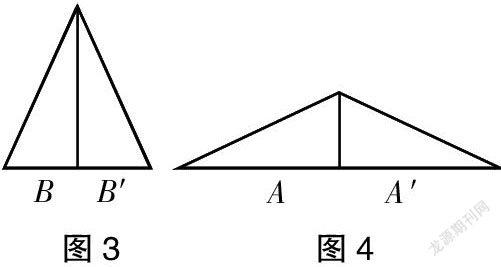
学生经过画一画、算一算、剪一剪得出:每个直角三角形的内角和都是180°。教师接着说:利用刚才剪开的两个三角形,能拼出一个大一点的三角形吗?拼一拼,想一想,拼成后的三角形的内角和是多少度?学生拼出来的三角形如图3、图4所示。
问:有办法计算这个三角形的内角和吗?学生观察拼出来的三角形,发现A、A′重合后原来的长方形长边上的两个直角重合了,形成了一个大的锐角三角形,计算得出锐角三角形的内角和是360°-2×90°=180°。很快学生又发现短边B、B′重合后,拼出来的三角形的内角和同样是360°-2×90°=180°。引导学生观察以上三种形状的三角形分别为直角三角形、锐角三角形和钝角三角形,它们的内角和都是180°。通过以上的实际操作、观察,学生发现三角形的内角和都是180°。
在学生的操作过程中,教师有序、有度、有方地引导。学生在量、剪、拼的过程中观察、思考、总结,形成动态的数学问题解决的认知过程,在實际操作中构建知识,发现规律,而这本身就是践行创新意识的过程。
三、融合数学问题解决策略,培养学生的推理能力
推理能力包括合情推理与演绎推理。新课标指出:合情推理是从已有事实出发,凭借经验和直觉,通过归纳和类比等推断某些结果;演绎推理是从已有的事实(包括定义、公理、定理等)和确定的规则(包括运算的定义、法则、顺序等)出发,按照逻辑推理的法则证明和计算[4]。应用数学知识解决问题在教学过程中,教师应提倡学生通过审题,然后分析数量关系再进行解答。在实际的教学中,容易发现,能找出数量关系的学生一定会解决问题;而大部分学生会列式解答,但说不出数量关系。要求学生列出数量关系再解答问题,往往学生是觉得困难的。究其原因,学生“知其然”往往比“知其所以然”来得容易一些。那么要如何有效地帮助学生根据已知条件整理出数量关系呢?
应用定义,引导学生审题,从已知条件中逐步深入,演绎分析出数量关系。学生在分析、推理的过程中,不仅“知其然”,而且还“知其所以然”。比如应用“分数乘法”解决问题时,需要从分数乘法的意义出发去解决问题。在解决问题的过程中,学生的推理能力得到培养。
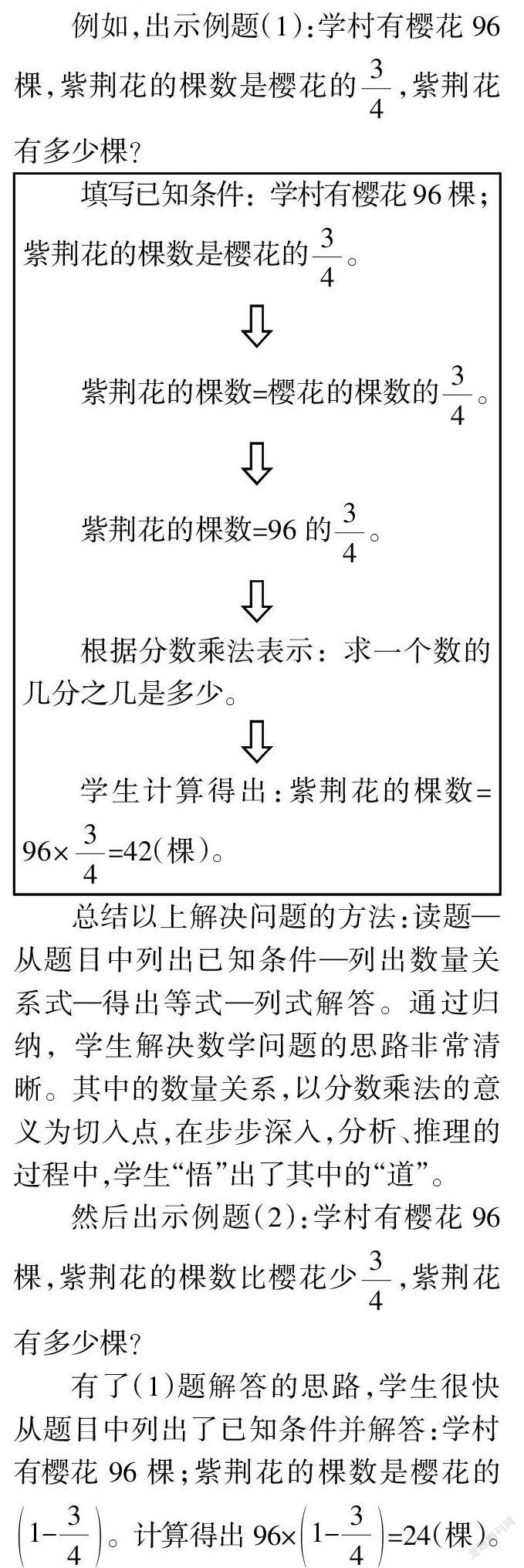
例如,出示例题(1):学村有樱花96棵,紫荆花的棵数是樱花的3/4,紫荆花有多少棵?
最后出示例题(3):学村有樱花96棵,紫荆花的棵数比樱花多3/4,紫荆花有多少棵?
要求学生先理出数量关系式再解答,很快学生就解决了问题。
随着课堂数学问题由简单到复杂再到应用,学生运用分数乘法的意义解决生活中的问题步步深入,课堂学习活动由教师的“教”转化成学生的“思”,最后由“思”去“动”、去“做”,独立分析问题中数量之间的关系,解决数学问题。这个过程引领着学生在学习知识的过程中懂得“用”已有的定义及规则解决问题。孔子说“学而不思则罔”,学习知识不是目的,而是经过个人的思考,在观察与思考过程中加以应用;在“用”中把知识转化为素养。培养学生数学学科核心素养,这才是教之道与学之本。
俗话说“教之道在于‘度’”。不管以何种策略培养学生的学科核心素养,都是以学生的生活经验为基础,融入生活信息,带有时代色彩。融入全程的实际操作,在动手实践与应用中,在“做”数学中“学”数学。从而实现现实世界的感悟与数学世界的感悟的关联与融合。在师生共同活动中,逐步培养学生数学学科知识的应用能力,唤醒学生潜在的创新意识。使学生在数学的感悟中,促进思考,促进发现,引领行为,一步一步地实现学科核心素养的形成与提升。
参考文献:
[1] 赵婀娜,赵婷玉. 中国学生发展核心素养发布[N]. 人民日报,2016-09-14.
[2] 余文森. 核心素养导向的课堂教学[M]. 上海:上海教育出版社,2017(2020.11重印).
[3] 余文森. 核心素养导向的课堂教学[M]. 上海:上海教育出版社,2017(2020.11重印).
[4] 中华人民共和国教育部制定. 义务教育数学课程标准[S]. 北京:北京师范大学出版社,2011(2019.7重印).
3590501908287
