考虑压-弯-扭耦合作用的开口截面杆件非线性静力模型

赵 云 丁 敏 韩盛柏 曹琼琼，2 蒋秀根*

(1.中国农业大学 水利与土木工程学院，北京 100083；2.铁总服务有限公司，北京 100844)

温室是现代农业生产中应用最为广泛的设施之一[1]。檩条是日光温室、连栋塑料温室、文洛型温室等温室结构中的纵向支撑构件，其受力变形情况比较复杂：一方面承受屋面重力荷载，产生弯曲及扭转位移；另一方面承受纵向风荷载，产生轴压变形；同时，由于雨水、雪水及温室室内高温高湿条件下大量水蒸汽上升形成的冷凝水均需集收及排出，温室内部檩条及檐口处天沟一般采用开口截面，以便集水排水，而开口截面杆件在压弯扭共同作用下存在复杂的翘曲扭转；另外，温室结构中的檩条通常为长细比较大的实腹开口截面直梁[2]，其截面形心与剪切中心常不重合，纵向失稳现象严重。作为温室结构中除主拱架之外最重要的结构构件[3]，檩条的强度及稳定安全性对温室结构整体安全性及稳定性分析具有重要意义。

目前对温室结构的研究多从温室光照、温度、湿度等环境因子角度出发，对温室结构力学性能的研究相对较少，温室结构设计及分析缺少完整和系统的行业及国家标准。已有研究大都选择利用ANSYS等有限元分析软件，在考虑特定影响因素的前提下，通过建模计算对温室结构在正常使用条件及典型灾害下的承载力情况进行分析[4-8]。然而，对于温室结构稳定承载力的研究多以整体结构为研究对象，对单个构件的受力变形特征及失稳分析的研究很少。因此，提供一个能够用于压弯扭组合荷载条件下，檩条几何非线性内力、变形、分岔失稳及极值点失稳的通用分析计算模型十分必要。

对温室结构中开口截面檩条，可按压-弯-扭耦合作用杆件进行内力、位移及稳定分析。对于压弯扭耦合作用杆件，已有研究在考虑特定影响因素的前提下提出了基于不同假定及侧重点的分析理论,对压弯扭耦合作用杆件的受力、位移及变形的基本特征进行阐述并给出失稳荷载等关键数据的计算方法[9-16]。然而，对于压弯扭耦合作用杆件的研究至今没有完善的理论体系，已有研究提出的分析理论及计算模型未综合考虑翘曲、大位移及剪切变形影响，势必对分析的准确性及模型计算精度、计算效率和普适性存在一定影响。

本研究旨在建立考虑压弯和压扭二阶效应的压弯扭杆件非线性静力分析模型，为温室结构中开口截面檩条的静力位移和内力以及压弯、压扭和弯扭稳定性分析提供依据。

1 基本模型与原理

1.1 模型参数与基本假定

按照右手螺旋法则建立三维坐标系(图1)：原点为杆件左截面形心，杆件轴线为x轴，向右为正；y轴垂直于杆件轴线，向上为正；z轴服从右手螺旋法则，向前为正。

杆件所受外荷载包括y方向分布力qy，x和z方向分布力矩mx及mz，外荷载与坐标轴方向一致为正；内力包括x方向轴力N、扭矩T，y方向竖向剪力Vy及法向弯矩Mz，z方向竖向弯矩My，当截面外法线方向与坐标轴正向一致时，截面内力与坐标方向一致为正，当截面外法线方向与坐标轴正向相反时，截面内力与坐标方向相反为正；初始内力包括x方向初始轴力N0及初始扭矩T0，y方向竖向初始剪力Vy0及法向初始弯矩Mz0，z方向竖向初始弯矩My0，方向定义与内力相同。

杆件位移包括x方向扭转角θx；y方向挠度v，竖向弯曲轴线转角φz，竖向弯曲截面转角θz，竖向剪切截面转角γz；z方向挠度w。杆件变形包括x方向扭率κx及y方向竖向弯曲曲率κz。杆件位移及变形方向均为与坐标轴一致为正。

Mz,Vy,T分别为杆件左端法向弯矩、竖向剪力及扭矩；Mz+dMz,Vy+dVy,T+dT分别为杆件右端法向弯矩，竖向剪力及扭矩；mx及mz为x、z方向分布力矩；qy为y方向分布力。

本研究中公式的推导过程基于以下假定：

1)将研究对象视为Timoshenko细长杆，即认为轴线转角为截面转角与剪切角之和。

2)采用Volasov约束扭转模型的基本理论[17]对杆件进行扭转分析，即认为杆件发生翘曲扭转时，截面剪应力及正应力同时存在。

3)采用Wanger翘曲模型的基本理论[18]对杆件进行翘曲分析，即认为杆件弯曲和扭转使得截面各点线位移不同，对应的纵向纤维合力不变、转角不同。

4)截面及杆件的压缩、弯曲、剪切及扭转均服从线弹性模型特征。

5)小变形，小转角：位移的高次微量为零；同时，对于截面角位移θ，存在sinθ=θ，cosθ=1，tanθ=θ

6)大位移，变形独立：位移对杆件的平衡条件造成影响，产生二阶内力；在计算二阶内力时，将初始内力参数看成是与变形无关的常数。

1.2 基本方程与控制方程

压弯扭杆件的位移控制方程以平衡方程、物理方程及几何方程为基础建立，为进行微段隔离体平衡分析建立平衡方程，需对微段二阶内力进行分析与计算。

1.2.1微段二阶内力原理

在轴压力、弯矩及扭矩耦合作用下，考虑大位移因素，初内力将产生二阶内力，其原理为：

1)微段截面上，挠度增量及扭转角增量使截面各点产生线位移增量，截面线位移增量导致微段纵向纤维出现转动增量。

2)微段各纤维的初应力为初内力在截面上的应力之和，包括初始正应力和初始剪应力，而且无论纤维如何转动，初始应力合力大小及方向保持不变。

3)微段上，由于纤维发生了转动，尽管纤维上应力总量不变，但纤维发生了切向及法向方向上的应力调整，调整前后的应力差值即为应力增量，应力增量包括初始正应力引起的正应力增量和剪应力增量、初始剪应力引起的正应力增量和剪应力增量。初应力产生的截面二阶应力见图2。

4)微段二阶内力即为应力增量在截面上对应的积分。根据产生原理，微段二阶内力的计算步骤为：首先对截面点位移进行分析，得到对应微段纤维倾角；然后计算初内力下的截面应力，并进行应力分解，进而求出应力增量；最后将应力增量在截面上进行积分运算，得到对应的微段二阶内力。

σ0为初始正应力；τ0为初始剪应力；dx，dφz，dv分别为微段长度、微段轴线转角及微段挠度增量。

1.2.2截面点位移分析

1.2.3微段二阶内力计算

根据二阶内力产生原理，结合截面点位移分析结果，将应力增量在截面上积分，可得微段二阶内力为：

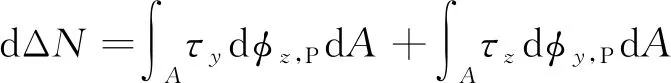
式中：dΔN,dΔVy及dΔT分别为微段二阶轴力，微段二阶剪力及微段二阶弯矩；τz及τy分别为z方向及y方向剪应力；σN,σMz及σMy分别为轴力、y方向弯矩及z方向弯矩产生的正应力。

1.2.4平衡方程

通过对微段进行平衡分析，建立考虑二阶内力的压弯扭杆件平衡方程。

微段竖向受力合为0，有Vy+dVy+dΔVy+qydx-Vy=0，进一步可写出竖向力平衡方程为：

(1)

(2)

微段轴向受力合为0，有T+dT+dΔT+mxdx-T=0，进一步可写出扭矩平衡方程为：

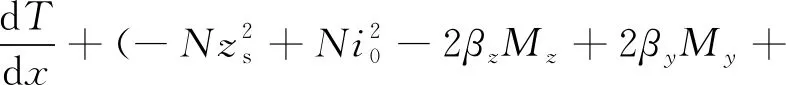
(3)

1.2.5几何方程及物理方程

几何方程为：

(4)

物理方程为：

(5)

式中：GId为圣维南抗扭刚度；E1Iw为约束扭转刚度；EIz为y方向弯曲刚度；GA/μ为剪切刚度。

1.2.6位移控制方程

综合平衡方程、物理方程及几何方程，式(1)～(5)，可以得到关于扭转角与挠度的压弯扭杆件位移控制方程为：

(6)

(7)

2 位移、变形与内力

2.1 位移

2.1.1位移控制方程的简化

位移控制方程为关于扭转角与挠度的4阶微分方程，由于不同结构的自由度数不同，为求解微分方程，需保证结构自由度数、微分方程阶数、微分方程通解项数、微分常系数数及边界条件数统一。因此，在不同结构下，需首先对位移控制方程进行阶数变换及消元变换。

1)自由扭转(E1Iw=0，GId≠0)。位移控制方程式(6)和式(7)为：

(8)

(9)

2)翘曲扭转(E1Iw≠0，GId≠0)。若My0-N0zs≠0，位移控制方程式(6)和式(7)为：

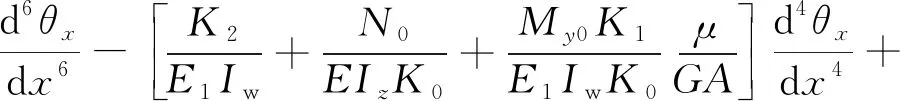
(10)

(11)

若My0-N0zs=0，位移控制方程式(6)和式(7)为：

(12)

(13)

2.1.2位移表达式

对简化后的位移控制方程式(8)～(13)进行求解，可以得到位移表达式的一般格式。求解式(8)及式(9)，可得自由扭转时扭转角和挠度表达式的一般格式。

当N0≠0时：

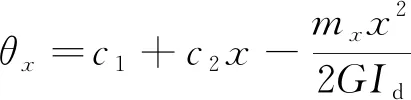
当N0=0时：

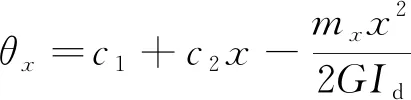
求解式(10)及式(11)，可得翘曲扭转且My0-N0zs≠0时扭转角和挠度表达式的一般格式。

当N0≠0时：

当N0=0时：

式中：

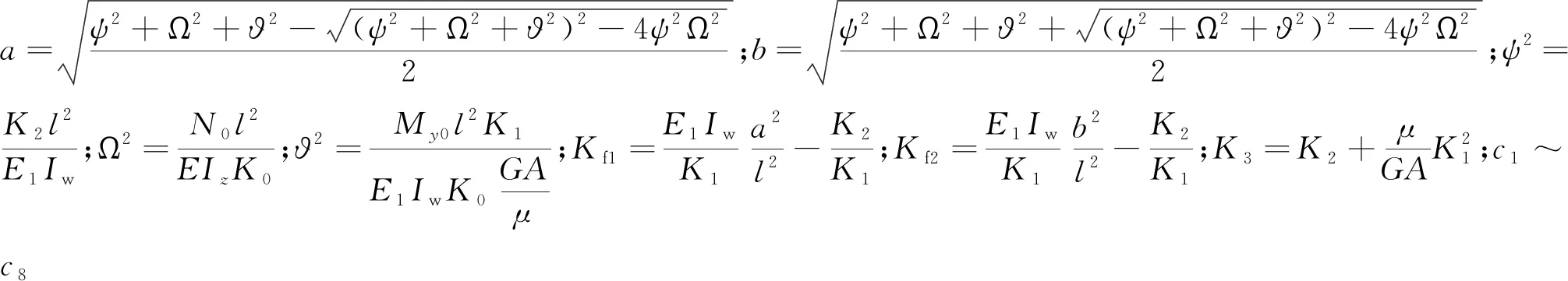
求解式(12)及式(13)，可得翘曲扭转且My0-N0zs=0时扭转角和挠度表达式的一般格式。

当N0≠0时：

当N0=0时：

特征根可分为实根、虚根、零根及重根，不同类型特征根对应位移表达式中的不同格式项，组合后可得到不同适用条件下扭转角及挠度表达式通解部分的简化格式，位移通解的简化格式见表1。

以扭转角和挠度表达式为基础，结合压弯扭杆件几何方程式(4)及物理方程式(5)，即可得到竖向轴线转角φz、竖向截面弯曲转角θz、竖向截面剪切转角γz的表达式。

表1 位移通解简化格式

2.2 变形及内力

以扭转角和挠度表达式为基础，结合压弯扭杆件几何方程式(4)及物理方程式(5)，即可得到扭率κx、翘曲率κ′x、竖向弯曲曲率κz及扭矩T、弯矩Mz、剪力Vy、双力矩B的表达式。

3 应用与算例

3.1 计算步骤

采用本研究提出的压弯扭杆件非线性静力计算模型进行计算时，首先需明确杆件边界条件，将其代入压弯扭杆件位移、变形及内力表达式，求出位移常系数；然后将位移常系数反代入压弯扭杆件位移、变形及内力表达式，得到对应的物理量方程；最后求出杆件任意位置的位移、变形及内力值。

3.1.1边界条件

压弯扭杆件的边界条件与支座形式直接相关，以铰支座为例，在杆件两端支座x=0和x=l处，边界条件为：扭转角为零，即θx(0)=θx(l)=0；挠度为零，即v(0)=v(l)=0；双力矩为零，即B(0)=B(l)=0；竖向弯曲曲率为零，即κz(0)=κz(l)=0。

3.1.2位移常系数求解

根据截面位移表达式及边界条件，可以得到压弯扭杆件位移常系数的定解方程为：

Ac+δq=δe

(14)

式中：A为依据各类边界条件，由杆件特定位置截面各物理量方程的基函数所组成的矩阵；δq为对应特解向量；δe为对应各特定位置截面物理量向量；c为位移常系数矩阵。

由方程式(14)，可得位移常系数的计算公式为：

c=A-1δe-A-1δq

(15)

3.2 算例分析

本研究中，将温室结构中开口截面檩条抽象为压-弯-扭耦合作用杆件，因而此处选取典型非完全对称开口截面杆件，采用本研究提出的计算模型计算其在5种不同荷载工况下的位移、变形及内力，并与文献[11]中的解析解进行比较，以验算本研究提出计算模型的适用性及准确性。

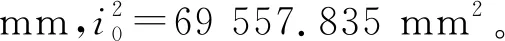
由表3可见，采用本研究提出的压弯扭杆件静力计算模型，当忽略剪切变形时，在5种荷载工况下，杆件变形、位移及内力计算结果与文献[11]中解析解完全相同(相对误差为0)。

考虑剪切变形时，与文献[11]中解析解相比：工况1，支座扭率减少10.19%，跨中扭转角减少5.12%，左支座扭矩增加0.73%，说明在集中扭矩荷载工况下，剪切变形不可忽略；工况2，支座扭率增加11.64%，跨中扭转角增加13.52%，左支座扭矩减少2.47%，说明在分布扭矩荷载工况下，剪切变形不可忽略；工况3，支座扭率、跨中扭转角及左支座扭矩变化量均在0.005%以下，说明在压扭荷载工况下，剪切变形可以忽略；工况4，左右支座扭率分别减少2.60%及3.89%，跨中扭转角减少5.72%，左支座扭矩增加3.31%，说明在弯扭荷载工况下，剪切变形不可忽略；工况5，除右支座扭率增加0.002%外，其余位移结果与文献解析解完全相同，说明在压弯扭荷载工况下，剪切变形可以忽略。5种荷载工况下，压扭及压弯扭荷载工况下的变形、位移及内力计算可忽略剪切变形影响，而集中扭矩、分布扭矩、弯扭荷载工况下的变形、位移及内力计算则不可忽略剪切变形影响。

计算结果表明，本研究得到的压弯扭杆件非线性静力计算模型可用于温室结构中开口截面檩条在任意荷载工况组合条件下的变形、内力及位移计算。同时，与文献[11]相比，本研究计算模型考虑了剪切变形的影响，计算结果更为精确合理。

表2 杆件承受的荷载工况

表3 不同荷载工况下杆件内力、变形及位移计算结果Table 3 Calculation results of internal force, deformation and deflection of the bar under different load cases

4 结束语

1)本研究在分析压弯扭杆件二阶内力的基础上，考虑了压-弯-扭耦合作用、约束翘曲、剪切变形等因素，建立了杆件微段隔离体平衡方程，结合几何方程及物理方程，推导出关于扭转角和挠度的位移控制方程，获得了压弯扭杆件非线性内力、位移及变形计算模型，并给出其计算步骤。

2)本研究提出的压弯扭杆件静力计算模型可适用于温室结构中开口截面檩条在任意荷载工况组合条件下的变形、位移及内力计算，计算结果准确可靠。

3)在温室结构开口截面檩条变形、位移及内力计算中，剪切变形的影响不可忽略。