基于ESPRIT 算法的频率分集雷达目标分离估计技术研究

陈新峰

（中国电子科技集团公司第二十七研究所，河南 郑州 450000）

1 概述

阵列扫描雷达以其灵活的波束控制能力得到广泛应用和快速的发展，其中相控阵雷达的应用最为广泛。传统的相控阵雷达主要通过子阵或者单元天线后接入移相器，对空间回波进行相位补偿，合成波束，具有快速，灵活、无机械惯性等优势。但是随着阵列规模增大，天线单元数越来越多，雷达设备的体积、重量、成本都面临重大挑战。

频率分集阵列（Frequency Diverse Array，简称 FDA）[1，2]由Antonikh 和Wicks 在2006 年国际雷达会议上首次提出，不同于一般的传统相控阵，频率分集阵列各相邻阵元间有一个远小于基准载频的频率偏移量，使得FDA 天线方向图同时依赖于角度、距离和时间。频率分集阵列中，由于各阵元辐射频率不同，其远场场强在空间相干叠加，使得波束主瓣能量在空间呈弯曲分布，也就是波束指向随着距离的变化而发生改变，从而实现空间波束扫描，这种方式比相控阵更为灵活，同时也降低了系统复杂度和功耗。其次，根据频率分集阵列的辐射特性，它可以在空间形成虚拟辐射源，当阵元间频率增量取合适的值时，虚拟辐射源与实际辐射源位置可相差十几公里，在现代化电子战中可以实现对敌电子欺骗和电磁干扰，有效提高己方雷达平台的安全性，这在实际雷达应用中具有重要意义。

有研究成果虽然分析了频控阵雷达波束的距离依赖特性，但如何利用这种特性的文献较少。一些学者指出这种特性可以用于抑制距离依赖性干扰，但没有给出具体的应用方案。实际上，频控阵雷达波束既具有目标距离依赖性，也具有目标方位角依赖性，但其距离向和方位角向存在耦合问题，所以常规频控阵雷达并不能完全抑制距离依赖性干扰。综合利用线性频控阵雷达的距离和方位角依赖特性，可以实现目标的到达距离和到达角二维联合估计。

2007 年，Mustafa Secmen 和 Simsek Demir 等人对FDA 空间波束扫描特性进行了分析，发现波束扫描在时间、距离和角度上呈周期性，并推导了波束扫描角随时间的变化规律[3]。文献[4]研究了波束指向和阵元间频率增量的关系。2008 和 2009 年，C.J.Baker 和 Karl Woodbridge等人设计了一个8 单元FDA 均匀线阵，并在微波实验室中对其辐射特性进行了测试[5，6]。

2 频率分集阵列信号模型

频率分集阵列雷达信号建模，以一维线阵为例，其阵列结构图如图1 所示。阵列中的每个天线单元发射一个具有频差的信号，例如第1 个单元发射射频信号频率为f0，第 2 个单元发射射频信号频率为 f0+Δf，第 n 个单元发射射频信号频率为 f0+（n-1）Δf。

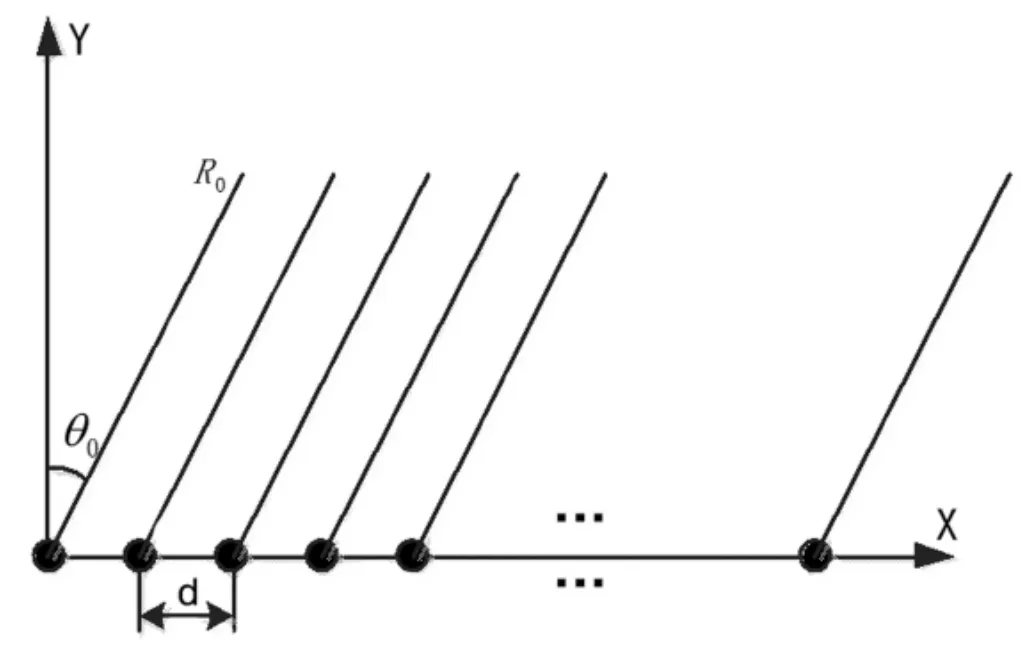
图1 天线阵列示意图

假设远场目标来波方向为θ0，距离为R0，阵元间距为d，基带信号为点频信号fB，根据相控阵类似的推导过程可以得到第n 个单元接收的回波信号为

上式中主要包含了7 项，经过解调后的基带信号项ej2πfBt可以记为 s（t），目标距离和方位都会在信号相位上产生影响。对式中最后一项进一步推导可以得到

因为每个阵元间发射信号的频偏非常小，所以Δf/f0＜＜1，因此最后一项的相位影响可以忽略不计，对相位的影响主要体现在后面5 项上，可以将后面5 项记为导向矢量an（R，θ），则阵列合成接收信号为：

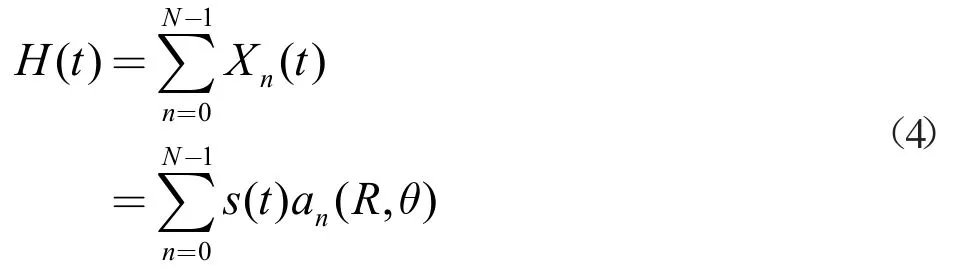
3 ESPRIT 算法

ESPRIT 是“Estimating signal parameters via rotational invariance techniques”的缩写，即为“通过旋转不变技术估计信号参数”。该算法的中心思想是利用子阵的平滑，平滑后的子阵与平滑前子阵的信号协方差矩阵仅仅相差一个由波达方向确定的旋转不变因子，然后可以通过旋转不变因子获得波达方向信息。同MUSIC 算法一样，ESPRIT 算法是空间DOA 估计中的另一个经典算法，它也需要对阵列接收数据的自相关矩阵进行特征值分解。但是这两种算法存在着明显的区别：MUSIC 算法利用信号方向向量与噪声子空间的正交性，而ESPRIT 算法利用子空间的旋转不变特性。ESPRIT 算法相比于MUSIC 算法，不需要进行谱峰搜索，因此大大降低了计算复杂度。

ESPRIT 算法的概念是由Roy 和Kailath 提出的。将阵列分成两个相同的子阵列。由于两个子阵的结构完全相同，对于同一个信号而言，两个子阵的输出只有一个相位差。下面假设两个子阵的接收数据如下：

子阵接收的信号可以选择在阵列流型上满足特定的关系，使得A1=A，A2=AΦ。信号的回波方向全部包含在A和Φ 中，只要能求解出其中一项就可以估计出信号方位。若使两个子阵相互错开一个阵元位置，其中的Φ 可以表示为

由上式可以看出Φ 是一个对角矩阵，且对角元素相同，为两个子阵由于阵列流型产生的相位差。Φ 称为旋转不变因子，求解出Φ，再根据对角元素与目标方位的关系就可以求得θ。

先将两个子阵的合并写成矩阵形式

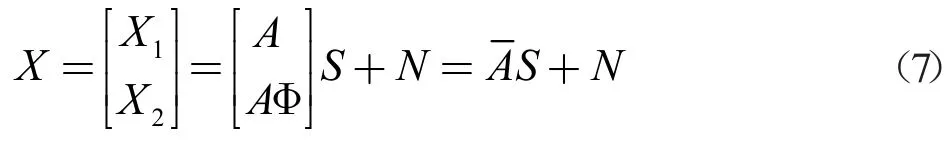
信号的协方差矩阵为

对协方差矩阵进行特征分解，得到下式

有唯一的非奇异矩阵

对两个子阵合并起来的子阵有相同的形式，所以有

子阵的信号子空间的关系如下

其中有

可以得到Φ 是等价于Ψ 的特征值构成的对角矩阵。所以一旦得到上述的旋转不变关系矩阵Ψ，就可以直接得到信号的入射角度。

4 FDA 阵列的旋转不变因子算法

根据ESPRIT 算法原理，应用到FDA 中，需要推导出相应的旋转不变因子，并且由于FDA 中目标的距离和方位是耦合的，要能解耦，分别得到距离、方位的二维估计。接下来先推导旋转不变因子，回顾下式。

上式中的时间函数中不包含距离、方位信息，因此只考虑和距离、方位信息有关的导向矢量，提出导向矢量并合并表达式可以得到

因此可以得到FDA 的旋转不变因子Φ 为

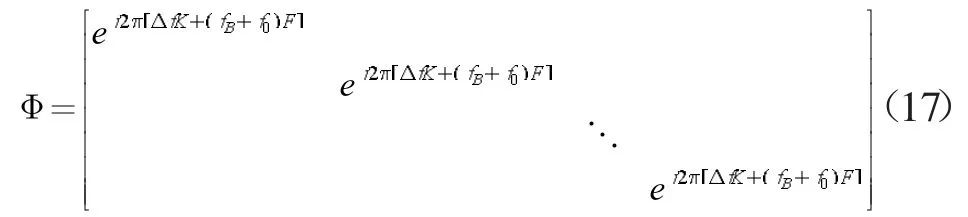
通过ESPRIT 算法计算求得矩阵Ψ，求得其特征值εi，计算特征值复角，有下式

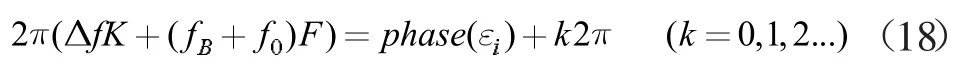
其中的k 为整数，求解K 和F，可以设计特定的Δf，设第一次发射频率间隔为Δf1，第二次发射频率间隔为Δf2，则有

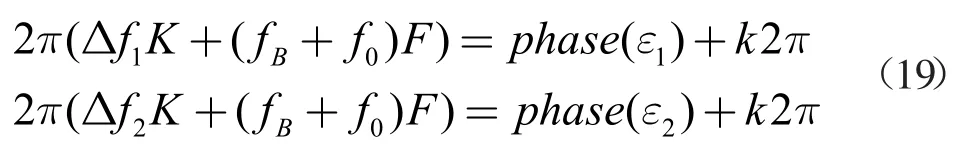
联立方程组可以求得

求解F 时，选取Δf 一致，改变阵列流型，反向排列一次数据可得到下式

联立方程组可以求得

5 算法仿真与分析

仿真实验中，雷达工作射频中心频率f0为10GHz，基带信号100MHz 点频信号，信噪比20dB，一维线阵单元天线个数22 个，采用点数200 个。仿真结果如表1 所示。

表1 仿真结果对照表

如表1 所示，给出了目标位于不同方位角与不同距离上时，应用文中提出的算法进行分离参数估计，仿真中设计两个频偏，其中 Δf1=10kHz，Δf2=10.1kHz，再通过阵列流型变换组合求解出距离与方位角估计值，可以看出在大信噪比下，能够准确地估计出目标距离与方位，同时由于该方法直接可以直接求解，省去了二维谱峰搜索，有效节省时间与计算资源。

接下来对不同信噪比情况下，算法的性能进行仿真实验，采用200 次蒙特卡洛仿真实验，仿真参数接收回波信号信噪比变化范围从-10dB 到30dB，仿真设置目标位于距离10.2km，方位4 度方向上。在每个信噪比条件下取多次计算的估计值与真实值误差的均方根值进行分析。仿真结果如图2、图3 所示。

从仿真结果中可以看出，在信噪比差的情况下，方位角与距离估计误差较大，随着信噪比提升，估计误差得到快速改善。在-10dB 至5dB 范围上，估计误差快速减小，在信噪比0dB 情况下，方位角估计误差小于0.005 度，距离估计误差小于200m。随着信噪比进一步改善估计结果误差还可以进一步提升但是改善效果趋于平缓。

图2 方位角估计误差仿真结果

图3 距离估计误差均方根仿真结果

6 结论

针对频率分集阵列雷达目标参数估计问题，为了避免二维谱峰搜索和解决频率分解目标方位-距离耦合问题。提出了采用旋转因子不变法进行两维分离参数估计的方法。通过设置不同的频率偏置与改变阵列流型，对方位-距离参数进行解耦和，通过构建回波的不同参数协方差矩阵，结合推导出的旋转不变因子，精确估计出目标方位、距离信息，并通过仿真验证了算法的正确性与有效性，算法可有效改善频率分集雷达参数估计的性能。